Sura ya 4 Mazoezi Mapitio
- Page ID
- 177567
Sura ya 4 Mazoezi Mapitio
Mfumo wa Kuratibu mstatili
Plot Pointi katika mfumo wa Kuratibu Rectangular
Katika mazoezi yafuatayo, njama kila hatua katika mfumo wa kuratibu mstatili.
- (-1, -5)
- (-3,4)
- (2, 1-3)
- \(\left(1, \frac{5}{2}\right)\)
- (4,3)
- (-4,3)
- (-4, -3)
- (4, 1-3)
- Jibu
-
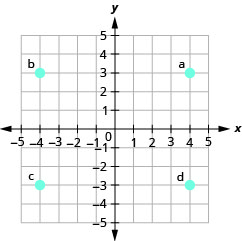
- (-2,0)
- (0, -4)
- (0,5)
- (3,0)
- \(\left(2, \frac{3}{2}\right)\)
- \(\left(3, \frac{4}{3}\right)\)
- \(\left(\frac{1}{3},-4\right)\)
- \(\left(\frac{1}{2},-5\right)\)
- Jibu
-
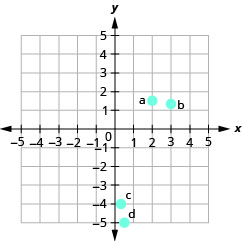
Tambua Pointi kwenye Grafu
Katika mazoezi yafuatayo, jina la jozi iliyoamriwa ya kila hatua iliyoonyeshwa kwenye mfumo wa kuratibu mstatili.
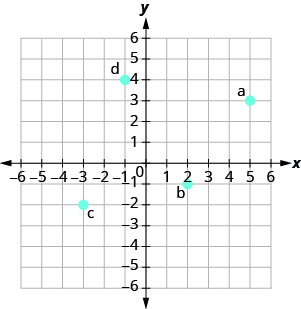
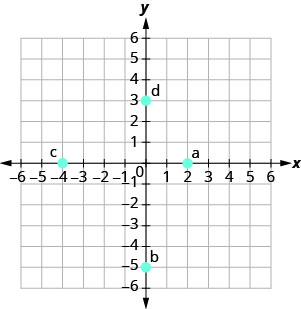
- Jibu
-
a. (2,0)
b (0, -5)
c (-4.0)
(0,3)
Thibitisha Ufumbuzi wa Equation katika Vigezo viwili
Katika mazoezi yafuatayo, ambayo iliamuru jozi ni ufumbuzi wa equations iliyotolewa?
\(5x+y=10\)
- (5,1)
- (2,0)
- (4, -10)
\(y=6x−2\)
- (1,4)
- \(\left(\frac{1}{3}, 0\right)\)
- (6,-2)
- Jibu
-
1, 2
Jaza Jedwali la Ufumbuzi wa Equation ya Mstari katika Vigezo viwili
Katika mazoezi yafuatayo, jaza meza ili kupata ufumbuzi kwa kila equation linear.
\(y=4 x-1\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -2 |
\(y=-\frac{1}{2} x+3\)
| x | y | (x, y) |
| 0 | ||
| 4 | ||
| -2 |
- Jibu
-
x y (x, y) 0 3 (0,3) 4 1 (4, 1) -2 4 (-2,4)
\(x+2 y=5\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -1 |
\(3x+2y=6\)
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -2 |
- Jibu
-
x y (x, y) 0 1-3 (0, 1-3) 2 0 (2,0) -2 -6 (-2, -6)
Pata ufumbuzi wa Equation ya Linear katika Vigezo viwili
Katika mazoezi yafuatayo, tafuta ufumbuzi wa tatu kwa kila equation linear.
\(x+y=3\)
\(x+y=-4\)
- Jibu
-
Majibu yatatofautiana.
\(y=3 x+1\)
\(y=-x-1\)
- Jibu
-
Majibu yatatofautiana.
Graphing Linear equations
Tambua Uhusiano Kati ya Ufumbuzi wa Equation na Grafu yake
Katika mazoezi yafuatayo, kwa kila jozi iliyoamriwa, chagua:
- Je, jozi iliyoamriwa ni suluhisho la equation?
- Je, ni hatua kwenye mstari?
\(y=−x+4\)
(0,4) (-1,3)
(2,2) (-2,6)
\(y=\frac{2}{3} x-1\)
\((0,-1) (3,1)\)
\((-3,-3) (6,4)\)
- Jibu
-
- ndiyo; ndiyo
- ndiyo; hapana
Grafu Ulinganisho wa Mstari na Pointi za Kupanga
Katika mazoezi yafuatayo, grafu kwa pointi za kupanga.
\(y=4x-3\)
\(y=-3x\)
- Jibu
-
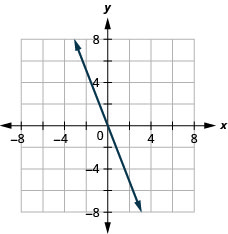
\(y=\frac{1}{2} x+3\)
\(x-y=6\)
- Jibu
-
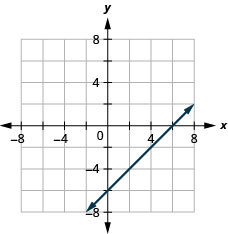
\(2x+y=7\)
\(3x-2y=6\)
- Jibu
-
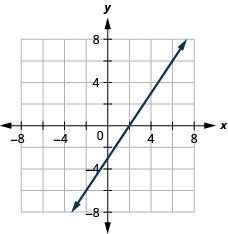
Grafu mistari ya wima na ya usawa
Katika mazoezi yafuatayo, graph kila equation.
\(y=-2\)
\(x=3\)
- Jibu
-
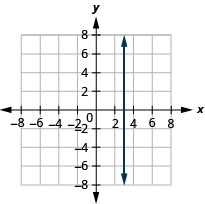
Katika mazoezi yafuatayo, grafu kila jozi ya equations katika mfumo huo wa kuratibu mstatili.
\(y=-2 x\)na\(y=-2\)
\(y=\frac{4}{3} x\)na\(y=\frac{4}{3}\)
- Jibu
-
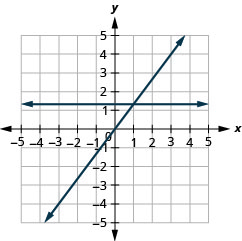
Graphing na Intercepts
Tambua\(x\) - na\(y\) -Intercepts kwenye Grafu
Katika mazoezi yafuatayo, pata\(x\) - na\(y\) -intercepts.
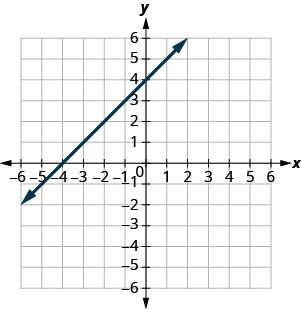
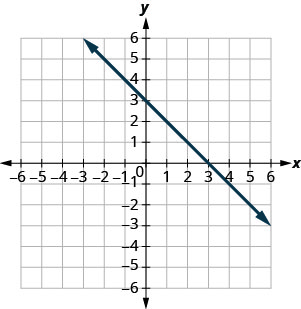
- Jibu
-
\((3,0)\)na\((0,3)\)
Kupata\(x\) - na\(y\) -Intercepts kutoka Equation ya Line
Katika mazoezi yafuatayo, pata maingiliano ya kila equation.
\(x+y=5\)
\(x-y=-1\)
- Jibu
-
\((-1,0),(0,1)\)
\(x+2y=6\)
\(2x+3y=12\)
- Jibu
-
\((6,0),(0,4)\)
\(y=\frac{3}{4} x-12\)
\(y=3x\)
- Jibu
-
\((0,0)\)
Grafu Mstari Kutumia Intercepts
Katika mazoezi yafuatayo, grafu kwa kutumia intercepts.
\(-x+3y=3\)
\(x+y=-2\)
- Jibu
-
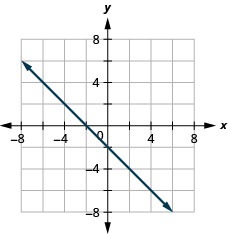
\(x-y=4\)
\(2x-y=5\)
- Jibu
-
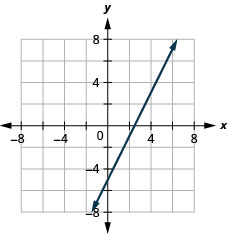
\(2x-4y=8\)
\(y=2x\)
- Jibu
-
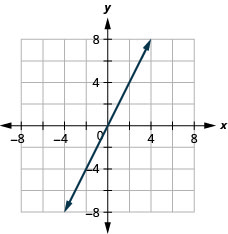
Mteremko wa Mstari
Tumia Geoboards kwa Model Slope
Katika mazoezi yafuatayo, tafuta mteremko unaoelekezwa kwenye kila geoboard.
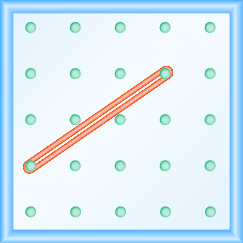
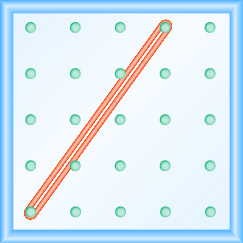
- Jibu
-
\(\frac{4}{3}\)
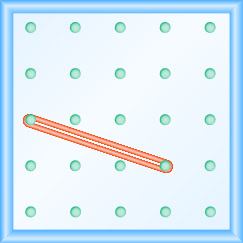
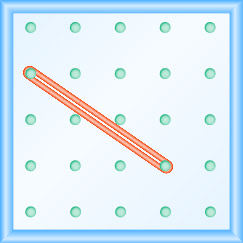
- Jibu
-
\(-\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{3}{2}\)
- Jibu
-
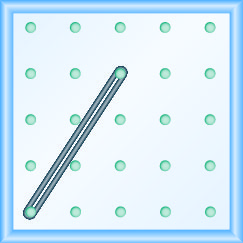
\(-\frac{2}{3}\)
\(-\frac{1}{2}\)
- Jibu
-
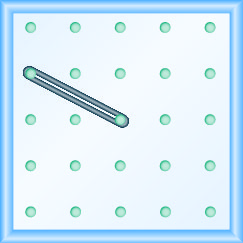
Tumia\(m=\frac{\text { rise }}{\text { run }}\) ili kupata Slope ya Line kutoka Grafu yake
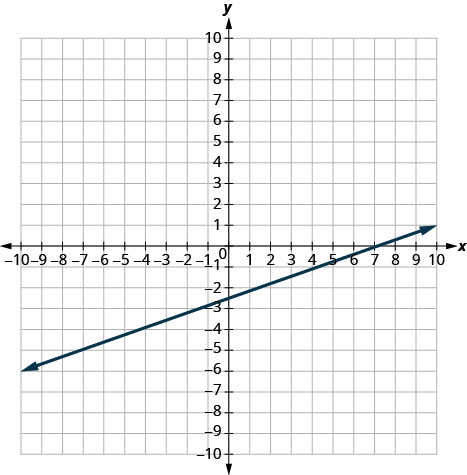
Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari umeonyeshwa.
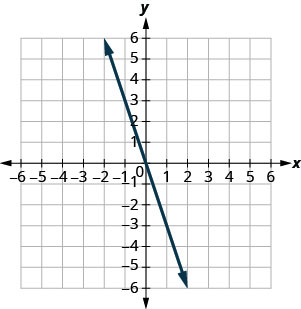
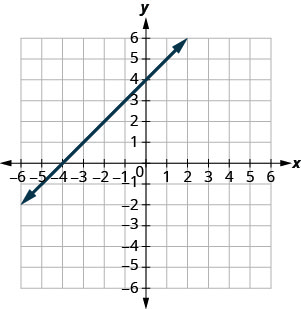
- Jibu
-
1
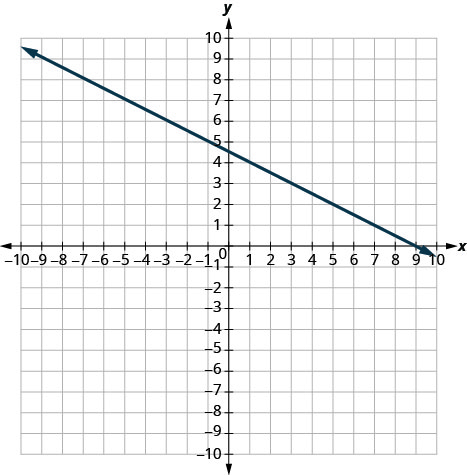
- Jibu
-
\(-\frac{1}{2}\)
Pata mteremko wa Mistari ya Ulalo na Wima
Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.
\(y=2\)
\(x=5\)
- Jibu
-
haijafafanuliwa
\(x=-3\)
\(y=-1\)
- Jibu
-
0
Tumia Mfumo wa Slope ili kupata mteremko wa Mstari kati ya Pointi mbili
Katika mazoezi yafuatayo, tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya kila jozi ya pointi.
\((-1,-1),(0,5)\)
\((3,5),(4,-1)\)
- Jibu
-
-6
\((-5,-2),(3,2)\)
\((2,1),(4,6)\)
- Jibu
-
\(\frac{5}{2}\)
Grafu Mstari Kutolewa Point na Slope
Katika mazoezi yafuatayo, grafu kila mstari na hatua iliyotolewa na mteremko.
\((2,-2) ; \quad m=\frac{5}{2}\)
\((-3,4) ; \quad m=-\frac{1}{3}\)
- Jibu
-
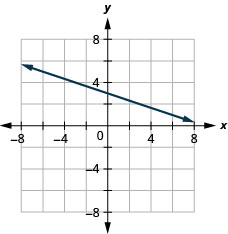
\(x\)-kukatiza\(-4 ; \quad m=3\)
\(y\)-kukatiza\(1 ; \quad m=-\frac{3}{4}\)
- Jibu
-
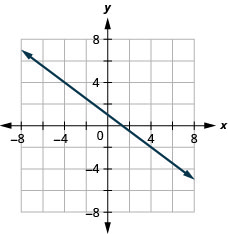
Kutatua Maombi ya mteremko
Katika mazoezi yafuatayo, tatua maombi haya ya mteremko.
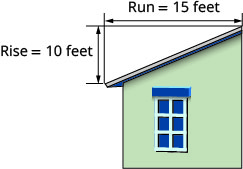
Paa iliyoonyeshwa hapa chini ina kupanda kwa\(10\) miguu na kukimbia kwa\(15\) miguu. Mteremko wake ni nini?
barabara mlima kuongezeka\(50\) miguu kwa\(500\) -foot kukimbia. Mteremko wake ni nini?
- Jibu
-
\(\frac{1}{10}\)
Piga Fomu ya Ulinganisho wa Mstari
Tambua Uhusiano Kati ya Grafu na Fomu ya Mteremo—Uingizaji wa Ulinganisho wa Mstari
Katika mazoezi yafuatayo, tumia grafu ili kupata mteremko na y -intercept ya kila mstari. Linganisha maadili kwa equation\(y=mx+b\).
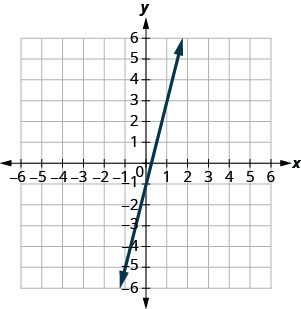
\(y=4x−1\)
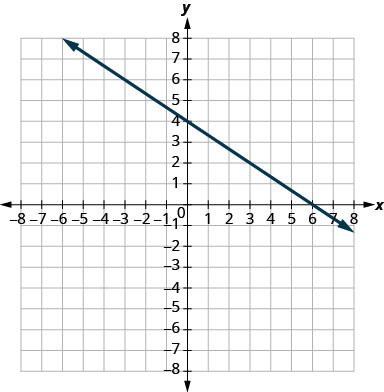
\(y=-\frac{2}{3} x+4\)
- Jibu
-
mteremko\(m=-\frac{2}{3}\) na\(y\) -intercept\((0,4)\)
Tambua mteremko na Y-intercept kutoka Equation ya Line
Katika mazoezi yafuatayo, tambua mteremko na\(y\) -intercept ya kila mstari.
\(y=-4 x+9\)
\(y=\frac{5}{3} x-6\)
- Jibu
-
\(\frac{5}{3} ;(0,-6)\)
\(5x+y=10\)
\(4x-5y=8\)
- Jibu
-
\(\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)\)
Grafu ya Mstari Kutumia mteremko wake na Ukataji
Katika mazoezi yafuatayo, graph mstari wa kila equation kwa kutumia mteremko wake na\(y\) -intercept.
\(y=2x+3\)
\(y=-x-1\)
- Jibu
-
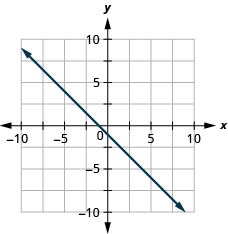
\(y=-\frac{2}{5} x+3\)
\(4x-3y=12\)
- Jibu
-
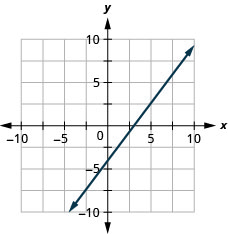
Katika mazoezi yafuatayo, tambua njia rahisi zaidi ya kuchora kila mstari.
\(x=5\)
\(y=-3\)
- Jibu
-
mstari usio na usawa
\(2x+y=5\)
\(x-y=2\)
- Jibu
-
ingilia kati
\(y=x+2\)
\(y=\frac{3}{4} x-1\)
- Jibu
-
pointi za kupanga njama
Grafu na Kutafsiri Matumizi ya mteremko — Intercept
Katherine ni chef binafsi. equation\(C=6.5m+42\) mifano uhusiano kati ya gharama yake ya kila wiki\(C\),, katika dola na idadi ya milo\(m\), kwamba yeye mtumishi.
- Kupata gharama Katherine kwa wiki wakati yeye mtumishi hakuna milo.
- Kupata gharama kwa wiki wakati yeye mtumishi\(14\) chakula.
- Tafsiri mteremko na\(C\) -intercept ya equation.
- Grafu equation.
Marjorie inafundisha piano. equation\(P=35h−250\) mifano uhusiano kati ya faida yake ya kila wiki,\(P\), katika dola na idadi ya masomo ya mwanafunzi,\(s\), kwamba yeye kufundisha.
- Kupata faida Marjorie kwa wiki wakati yeye anafundisha hakuna masomo mwanafunzi.
- Pata faida kwa wiki wakati anafundisha masomo ya\(20\) wanafunzi.
- Tafsiri mteremko na\(P\) -intercept ya equation.
- Grafu equation.
- Jibu
-
- \(−$250\)
- \($450\)
- mteremko,\(35\), ina maana kwamba Marjorie ya faida ya kila wiki,\(P\), kuongezeka\($35\) kwa kwa kila somo ziada mwanafunzi yeye anafundisha. The\(P\) -intercept ina maana kwamba wakati idadi ya masomo ni\(0\), Marjorie hupoteza\($250\).
Tumia Materemko Kutambua Mistari Sambamba
Katika mazoezi yafuatayo, tumia mteremko na\(y\) -intercepts kuamua kama mistari ni sambamba.
\(4x-3y=-1 ; \quad y=\frac{4}{3} x-3\)
\(2 x-y=8 ; \quad x-2 y=4\)
- Jibu
-
si sambamba
Tumia Materemko ya Kutambua Mipangilio ya Per
Katika mazoezi yafuatayo, tumia mteremko na y-intercepts kuamua kama mistari ni perpendicular.
\(y=5x-1 ; \quad 10x+2y=0\)
\(3x-2y=5 ; \quad 2x+3y=6\)
- Jibu
-
wima
Pata Equation ya Mstari
Kupata Equation ya Line Kutokana na mteremko na y -Intercept
Katika mazoezi yafuatayo, pata usawa wa mstari na mteremko uliopewa na\(y\) -intercept. Andika equation katika mteremka-intercept fomu.
mteremko\(\frac{1}{3}\) na\(y\) -intercept\((0,-6)\)
mteremko\(-5\) na\(y\) -intercept\((0,-3)\)
- Jibu
-
\(y=-5x-3\)
mteremko\(0\) na\(y\) -intercept\((0,4)\)
mteremko\(-2\) na\(y\) -intercept\((0,0)\)
- Jibu
-
\(y=-2x\)
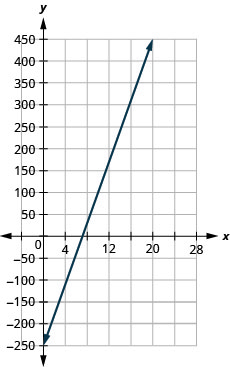
Katika mazoezi yafuatayo, pata usawa wa mstari ulioonyeshwa kwenye kila grafu. Andika equation katika mteremka-intercept fomu.
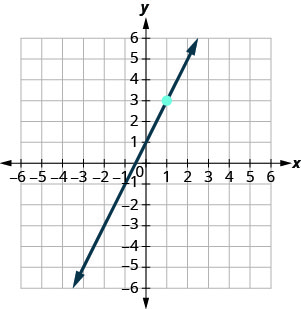
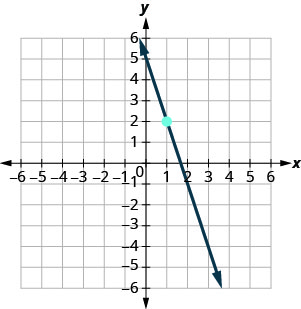
- Jibu
-
\(y=-3x+5\)
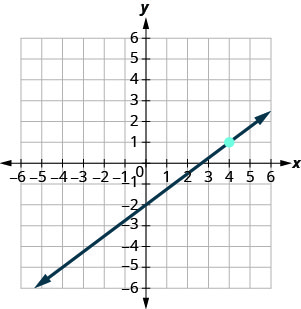
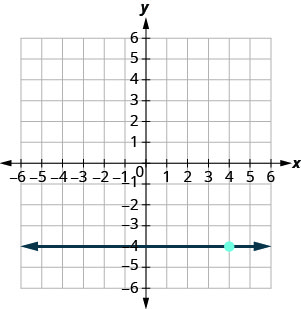
- Jibu
-
\(y=-4\)
Kupata Equation ya Line Kutokana na mteremko na Point
Katika mazoezi yafuatayo, pata usawa wa mstari na mteremko uliopewa na una uhakika uliopewa. Andika equation katika mteremka-intercept fomu.
\(m=-\frac{1}{4},\)elekeza\((-8,3)\)
\(m=\frac{3}{5},\)elekeza\((10,6)\)
- Jibu
-
\(y=\frac{3}{5} x\)
Mstari wa usawa ulio na\((-2,7)\)
\(m=-2,\)elekeza\((-1,-3)\)
- Jibu
-
\(y=-2x-5\)
Kupata Equation ya Line Kutokana Pointi mbili
Katika mazoezi yafuatayo, pata usawa wa mstari ulio na pointi zilizopewa. Andika equation katika mteremka-intercept fomu.
\((2,10)\)na\((-2,-2)\)
\((7,1)\)na\((5,0)\)
- Jibu
-
\(y=\frac{1}{2} x-\frac{5}{2}\)
\((3,8)\)na\((3,-4)\)
\((5,2)\)na\((-1,2)\)
- Jibu
-
\(y=2\)
Pata Equation ya Mstari Sambamba na Line Iliyopewa
Katika mazoezi yafuatayo, pata usawa wa mstari unaofanana na mstari uliopewa na una uhakika uliopewa. Andika equation katika mteremka-intercept fomu.
\(y=-3x+6,\)uhakika wa mstari\((1,-5)\)
\(2x+5y=-10,\)uhakika wa mstari\((10,4)\)
- Jibu
-
\(y=-\frac{2}{5} x+8\)
\(x=4,\)uhakika wa mstari\((-2,-1)\)
\(y=-5,\)uhakika wa mstari\((-4,3)\)
- Jibu
-
\(y=3\)
Kupata Equation ya Line Perpendicular kwa Line Kutokana
Katika mazoezi yafuatayo, pata equation ya mstari perpendicular kwa mstari uliopewa na ina uhakika fulani. Andika equation katika mteremka-intercept fomu.
\(y=-\frac{4}{5} x+2,\)uhakika wa mstari\((8,9)\)
\(2x-3y=9,\)uhakika wa mstari\((-4,0)\)
- Jibu
-
\(y=-\frac{3}{2} x-6\)
\(y=3,\)uhakika wa mstari\((-1,-3)\)
\(x=-5\)uhakika wa mstari\((2,1)\)
- Jibu
-
\(y=1\)
Graph Linear kutofautiana
Thibitisha Ufumbuzi wa Usawa katika Vigezo viwili
Katika mazoezi yafuatayo, onyesha kama kila jozi iliyoamriwa ni suluhisho la usawa uliotolewa.
Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y<x−3\):
- \((0,1)\)
- \((−2,−4)\)
- \((5,2)\)
- \((3,−1)\)
- \((−1,−5)\)
Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(x+y>4\):
- \((6,1)\)
- \((−3,6)\)
- \((3,2)\)
- \((−5,10)\)
- \((0,0)\)
- Jibu
-
- ndiyo
- hapana
- ndiyo
- ndiyo
- hapana
Tambua Uhusiano Kati ya Ufumbuzi wa Usawa na Grafu yake
Katika mazoezi yafuatayo, weka usawa unaoonyeshwa na eneo la kivuli.
Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=−x+2\).
Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=\frac{2}{3} x-3\)
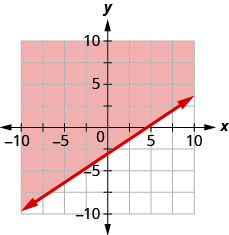
- Jibu
-
\(y>\frac{2}{3} x-3\)
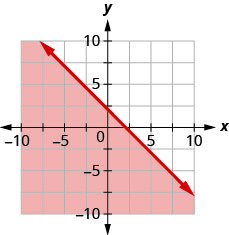
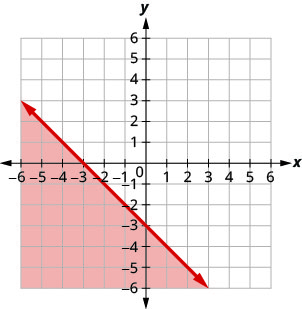
Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x+y=−4\).
Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x−2y=6\).
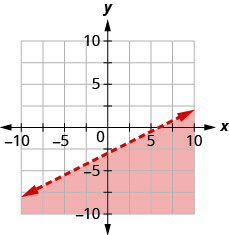
- Jibu
-
\(x-2 y \geq 6\)
Graph Linear kutofautiana
Katika mazoezi yafuatayo, grafu kila usawa wa mstari.
Grafu usawa wa mstari\(y>\frac{2}{5} x-4\)
Grafu usawa wa mstari\(y \leq-\frac{1}{4} x+3\)
- Jibu
-
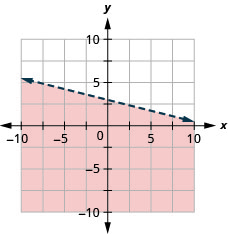
Grafu usawa wa mstari\(x-y \leq 5\)
Grafu usawa wa mstari\(3 x+2 y>10\)
- Jibu
-
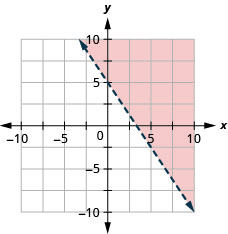
Grafu usawa wa mstari\(y \leq-3 x\)
Grafu usawa wa mstari\(y<6\)
- Jibu
-
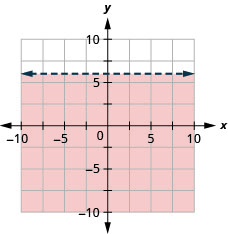
Mazoezi mtihani
Panda kila hatua katika mfumo wa kuratibu mstatili.
- \((2,5)\)
- \((−1,−3)\)
- \((0,2)\)
- \(\left(-4, \frac{3}{2}\right)\)
- \((5,0)\)
Ni ipi kati ya jozi zilizopewa zilizoamriwa ni ufumbuzi wa equation\(3x−y=6\)?
- \((3,3)\)
- \((2,0)\)
- \((4,−6)\)
- Jibu
-
- ndiyo
- ndiyo
- hapana
Pata ufumbuzi wa tatu kwa equation linear\(y=-2x-4\)
Kupata\(x\) - na\(y\) -intercepts ya equation\(4x-3y=12\)
- Jibu
-
\((3,0),(0,-4)\)
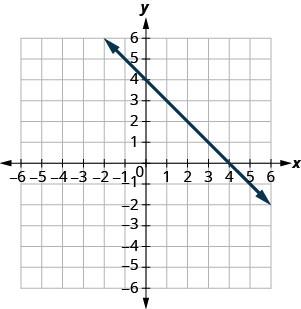
Pata mteremko wa kila mstari umeonyeshwa.
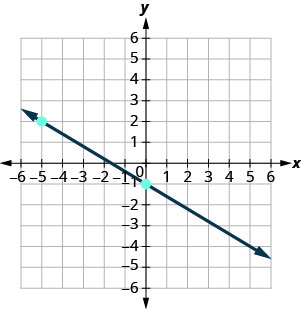
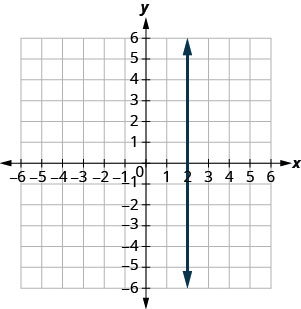
- Jibu
-
haijafafanuliwa
Pata mteremko wa mstari kati ya pointi\((5,2)\) na\((-1,-4)\)
- Jibu
-
1
Grafu mstari na mteremko\(\frac{1}{2}\) ulio na uhakika\((-3,-4)\)
Grafu mstari kwa kila moja ya equations zifuatazo.
\(y=\frac{5}{3} x-1\)
- Jibu
-
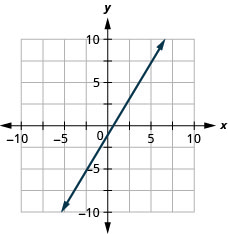
\(y=-x\)
\(x-y=2\)
- Jibu
-
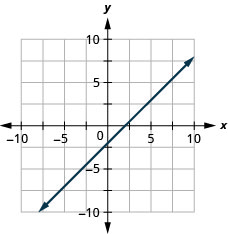
\(4x+2y=-8\)
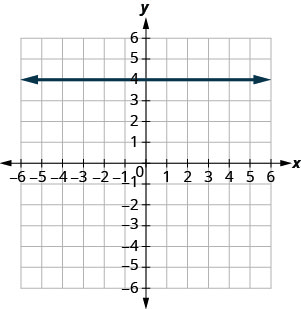
\(y=2\)
- Jibu
-
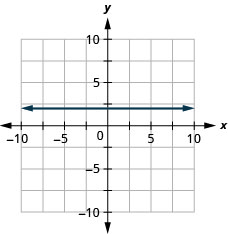
\(x=-3\)
Kupata equation ya kila mstari. Andika equation katika mteremka-intercept fomu.
mteremko\(-\frac{3}{4}\) na\(y\) -intercept\((0,-2)\)
- Jibu
-
\(y=-\frac{3}{4} x-2\)
\(m=2,\)elekeza\((-3,-1)\)
zenye\((10,1)\) na\((6,-1)\)
- Jibu
-
\(y=\frac{1}{2} x-4\)
sambamba na mstari\(y=-\frac{2}{3} x-1,\) ulio na uhakika\((-3,8)\)
perpendicular kwa mstari\(y=\frac{5}{4} x+2,\) ulio na uhakika\((-10,3)\)
- Jibu
-
\(y=-\frac{4}{5} x-5\)
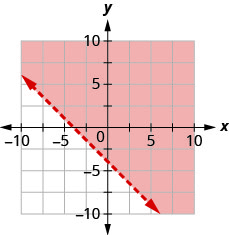
Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=−x−3\).
Graph kila usawa linear.
\(y>\frac{3}{2} x+5\)
- Jibu
-
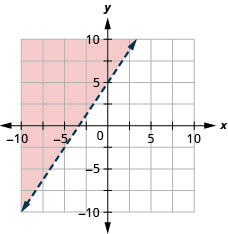
\(x-y \geq-4\)
\(y \leq-5 x\)
- Jibu
-
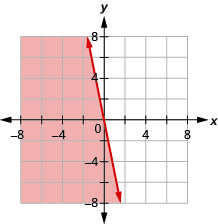
\(y<3\)