Skip to main content
Global

4.7E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    177625

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Thibitisha Ufumbuzi wa Usawa katika Vigezo viwili

    Katika mazoezi yafuatayo, onyesha kama kila jozi iliyoamriwa ni suluhisho la usawa uliotolewa.

    Zoezi\(\PageIndex{1}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y>x−1\):

    1. \((0,1)\)
    2. \((−4,−1)\)
    3. \((4,2)\)
    4. \((3,0)\)
    5. \((−2,−3)\)
    Zoezi\(\PageIndex{2}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y>x−3\):

    1. \((0,0)\)
    2. \((2,1)\)
    3. \((−1,−5)\)
    4. \((−6,−3)\)
    5. \((1,0)\)
    Jibu
    1. ndiyo
    2. hapana
    3. hapana
    4. ndiyo
    5. hapana
    Zoezi\(\PageIndex{3}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y<x+2\):

    1. \((0,3)\)
    2. \((−3,−2)\)
    3. \((−2,0)\)
    4. \((0,0)\)
    5. \((−1,4)\)
    Zoezi\(\PageIndex{4}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y<x+5\):

    1. \((−3,0)\)
    2. \((1,6)\)
    3. \((−6,−2)\)
    4. \((0,1)\)
    5. \((5,−4)\)
    Jibu
    1. ndiyo
    2. hapana
    3. hapana
    4. ndiyo
    5. ndiyo
    Zoezi\(\PageIndex{5}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(x+y>4\):

    1. \((5,1)\)
    2. \((−2,6)\)
    3. \((3,2)\)
    4. \((10,−5)\)
    5. \((0,0)\)
    Zoezi\(\PageIndex{6}\)

    Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(x+y>2\):

    1. \((1,1)\)
    2. \((4,−3)\)
    3. \((0,0)\)
    4. \((−8,12)\)
    5. \((3,0)\)
    Jibu
    1. hapana
    2. hapana
    3. hapana
    4. ndiyo
    5. ndiyo

    Tambua Uhusiano Kati ya Ufumbuzi wa Usawa na Grafu yake

    Katika mazoezi yafuatayo, weka usawa unaoonyeshwa na eneo la kivuli.

    Zoezi\(\PageIndex{7}\)

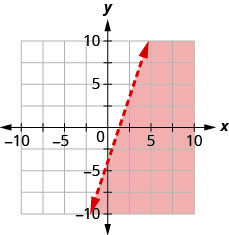
    Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=3x−4\).

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na 3x minus 4 ni njama kama mstari dashed kupanua kutoka chini kushoto kuelekea kulia juu. Kanda ya haki ya mstari ni kivuli.

    Zoezi\(\PageIndex{8}\)

    Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=2x−4\).

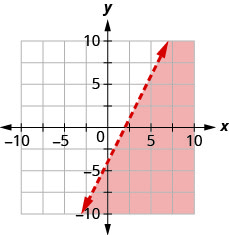
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na 2x minus 4 imepangwa kama mstari imara kupanua kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Jibu

    \(y<2 x-4\)

    Zoezi\(\PageIndex{9}\)

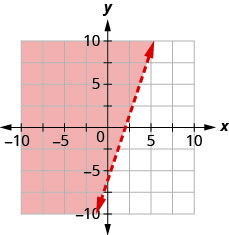
    Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=\frac{1}{2} x+1\)

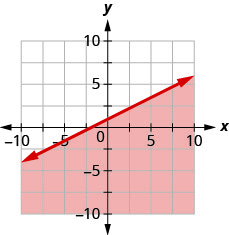
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na nusu moja x pamoja na 1 imepangwa kama mstari imara unaoenea kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{10}\)

    Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=-\frac{1}{3} x-2\)

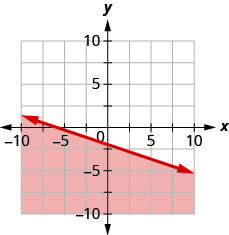
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na hasi moja ya tatu x minus 2 imepangwa kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Kanda iliyo chini ya mstari ni kivuli.

    Jibu

    \(y \leq-\frac{1}{3} x-2\)

    Zoezi\(\PageIndex{11}\)

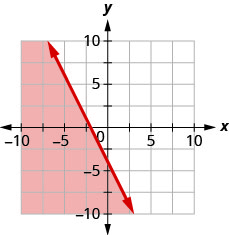
    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x+y=5\).

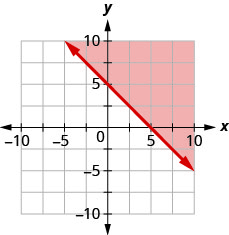
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x plus y sawa na 5 ni njama kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Mkoa ulio juu ya mstari umevuliwa.

    Zoezi\(\PageIndex{12}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x+y=3\).

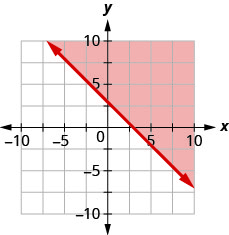
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x plus y ni sawa na 3 ni njama kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Mkoa ulio juu ya mstari umevuliwa.

    Jibu

    \(x+y \geq 3\)

    Zoezi\(\PageIndex{13}\)

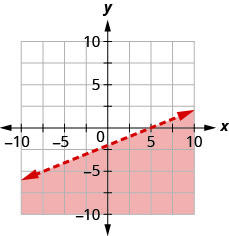
    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(2x+y=−4\).

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 2 x pamoja na y sawa na hasi 4 hupangwa kama mstari imara unaoenea kutoka juu kushoto kuelekea chini ya kulia. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{14}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x+2y=−2\).

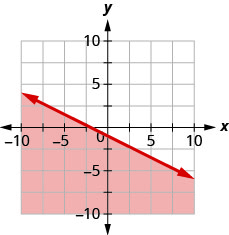
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x pamoja na 2 y sawa na hasi 2 imepangwa kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Kanda iliyo chini ya mstari ni kivuli.

    Jibu

    \(x+2 y \geq-2\)

    Zoezi\(\PageIndex{15}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(3x−y=6\).

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 3 x minus y sawa na 6 umepangwa kama mstari uliopigwa unaotembea kutoka chini kushoto kuelekea kulia juu. Kanda upande wa kushoto wa mstari ni kivuli.

    Zoezi\(\PageIndex{16}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(2x−y=4\).

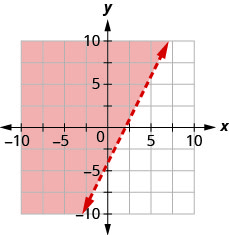
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 2 x minus y sawa na 4 umepangwa kama mstari uliopigwa unaotembea kutoka chini kushoto kuelekea kulia juu. Kanda upande wa kushoto wa mstari ni kivuli.

    Jibu

    \(2 x-y<4\)

    Zoezi\(\PageIndex{17}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(2x−5y=10\).

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 2 x minus 5 y ni sawa na 10 imepangwa kama mstari uliopigwa unaoenea kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{18}\)

    Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(4x−3y=12\).

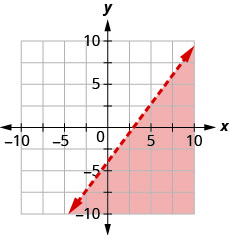
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 4 x minus 3 y sawa na 12 umepangwa kama mstari uliopigwa unaotembea kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Jibu

    \(4 x-3 y>12\)

    Graph Linear kutofautiana

    Katika mazoezi yafuatayo, grafu kila usawa wa mstari.

    Zoezi\(\PageIndex{19}\)

    Grafu usawa wa mstari\(y>\frac{2}{3} x-1\)

    Zoezi\(\PageIndex{20}\)

    Grafu usawa wa mstari\(y<\frac{3}{5} x+2\)

    Jibu

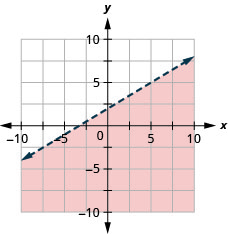
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na tatu ya tano x pamoja na 2 imepangwa kama mstari uliopigwa unaoenea kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{21}\)

    Grafu usawa wa mstari\(y \leq-\frac{1}{2} x+4\)

    Zoezi\(\PageIndex{22}\)

    Grafu usawa wa mstari\(y \geq-\frac{1}{3} x-2\)

    Jibu

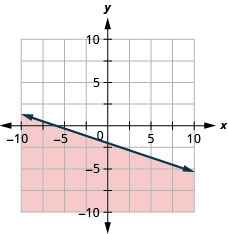
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na hasi moja ya tatu x minus 2 imepangwa kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{23}\)

    Grafu usawa wa mstari\(x-y \leq 3\)

    Zoezi\(\PageIndex{24}\)

    Grafu usawa wa mstari\(x-y \geq -2\)

    Jibu

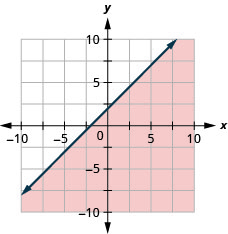
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x minus y sawa na hasi 2 ni njama kama mstari imara kupanua kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{25}\)

    Grafu usawa wa mstari\(4x+y>-4\)

    Zoezi\(\PageIndex{26}\)

    Grafu usawa wa mstari\(x+5y<-5\)

    Jibu

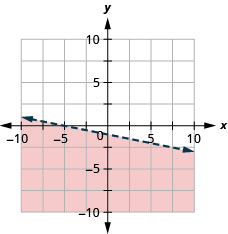
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x pamoja na 5 y sawa na hasi 5 hupangwa kama mstari uliopigwa unaotembea kutoka juu kushoto kuelekea chini ya kulia. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{27}\)

    Grafu usawa wa mstari\(3 x+2 y \geq-6\)

    Zoezi\(\PageIndex{28}\)

    Grafu usawa wa mstari\(4 x+2 y \geq-8\)

    Jibu

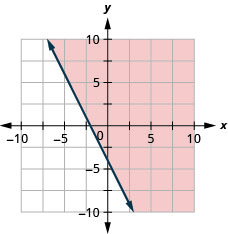
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari wa 4 x pamoja na 2 y sawa na hasi 8 hupangwa kama mstari imara unaoenea kutoka juu kushoto kuelekea chini ya kulia. Kanda ya haki ya mstari ni kivuli.

    Zoezi\(\PageIndex{29}\)

    Grafu usawa wa mstari\(y>4x\)

    Zoezi\(\PageIndex{30}\)

    Grafu usawa wa mstari\(y>x\)

    Jibu

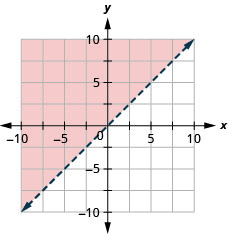
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y sawa x ni njama kama mstari imara kupanua kutoka chini kushoto kuelekea kulia juu. Mkoa ulio juu ya mstari umevuliwa.

    Zoezi\(\PageIndex{31}\)

    Grafu usawa wa mstari\(y \leq-x\)

    Zoezi\(\PageIndex{32}\)

    Grafu usawa wa mstari\(y \leq-3 x\)

    Jibu

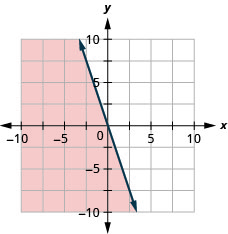
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na hasi 3 x ni njama kama mstari imara kupanua kutoka juu kushoto kuelekea chini kulia. Kanda upande wa kushoto wa mstari ni kivuli.

    Zoezi\(\PageIndex{33}\)

    Grafu usawa wa mstari\(y \geq-2\)

    Zoezi\(\PageIndex{34}\)

    Grafu usawa wa mstari\(y<-1\)

    Jibu

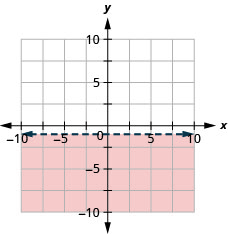
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y sawa na hasi 1 hupangwa kama mstari wa usawa. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{35}\)

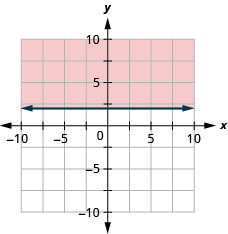
    Grafu usawa wa mstari\(y<4\)

    Zoezi\(\PageIndex{36}\)

    Grafu usawa wa mstari\(y \geq 2\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y sawa na 2 ni njama kama mstari imara usawa. Mkoa ulio juu ya mstari umevuliwa.

    Zoezi\(\PageIndex{37}\)

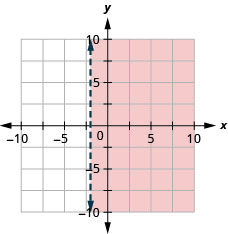
    Grafu usawa wa mstari\(x \leq 5\)

    Zoezi\(\PageIndex{38}\)

    Grafu usawa wa mstari\(x>-2\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x sawa na hasi 2 hupangwa kama mstari wa wima uliopigwa. Kanda ya haki ya mstari ni kivuli.

    Zoezi\(\PageIndex{39}\)

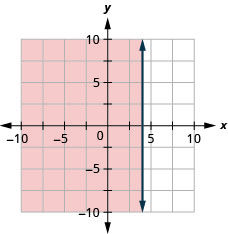
    Grafu usawa wa mstari\(x>-3\)

    Zoezi\(\PageIndex{40}\)

    Grafu usawa wa mstari\(x \leq 4\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x sawa na 4 hupangwa kama mstari wa wima imara. Kanda upande wa kushoto wa mstari ni kivuli.

    Zoezi\(\PageIndex{41}\)

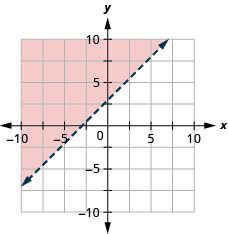
    Grafu usawa wa mstari\(x-y<4\)

    Zoezi\(\PageIndex{42}\)

    Grafu usawa wa mstari\(x-y<-3\)

    Jibu

    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x minus y sawa na hasi 3 imepangwa kama mstari uliopigwa unaoenea kutoka chini kushoto kuelekea kulia juu. Mkoa ulio juu ya mstari umevuliwa.

    Zoezi\(\PageIndex{43}\)

    Grafu usawa wa mstari\(y \geq \frac{3}{2} x\)

    Zoezi\(\PageIndex{44}\)

    Grafu usawa wa mstari\(y \leq \frac{5}{4} x\)

    Jibu

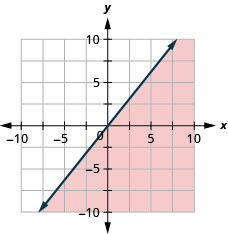
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na nne tano x ni njama kama mstari imara kupanua kutoka chini kushoto kuelekea kulia juu. Kanda iliyo chini ya mstari ni kivuli.

    Zoezi\(\PageIndex{45}\)

    Grafu usawa wa mstari\(y>-2 x+1\)

    Zoezi\(\PageIndex{46}\)

    Grafu usawa wa mstari\(y<-3 x-4\)

    Jibu

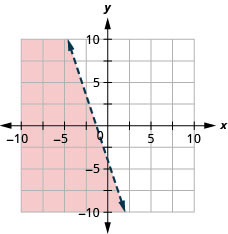
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari y ni sawa na hasi 3 x minus 4 imepangwa kama mstari uliopigwa unaotembea kutoka juu kushoto kuelekea chini ya kulia. Kanda upande wa kushoto wa mstari ni kivuli.

    Zoezi\(\PageIndex{47}\)

    Grafu usawa wa mstari\(x \leq-1\)

    Zoezi\(\PageIndex{48}\)

    Grafu usawa wa mstari\(x \geq 0\)

    Jibu

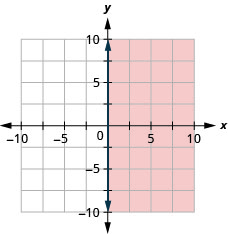
    Grafu inaonyesha ndege ya kuratibu x y. Ya x- na y-axes kila kukimbia kutoka hasi 10 hadi 10. Mstari x sawa na hasi 0 hupangwa kama mstari wa wima imara kando ya mhimili wa y. Kanda ya haki ya mstari ni kivuli.

    kila siku Math

    Zoezi\(\PageIndex{49}\)

    Fedha. Gerry anataka kuwa na kiwango cha juu cha $100 fedha katika kibanda tiketi wakati kanisa lake kanisa kufungua. Atakuwa na $1 bili na $5 bili. Kama\(x\) ni idadi ya $1 bili na\(y\) ni idadi ya $5 bili, usawa\(x+5y \leq 100\) mifano hali.

    1. Grafu usawa.
    2. Orodha ya ufumbuzi wa tatu kwa usawa\(x+5y \leq 100\) ambapo wote wawili\(x\) na\(y\) ni integers.
    Zoezi\(\PageIndex{50}\)

    Ununuzi. Tula ina dola 20 za kutumia katika uuzaji wa kitabu kilichotumiwa. Vitabu vya Hardcover vina gharama $2 kila mmoja na vitabu vya karatasi vina gharama $0.50 kila mmoja. Kama\(x\) ni idadi ya vitabu hardcover Tula anaweza kununua na\(y\) ni idadi ya vitabu Paperback anaweza kununua, usawa\(2x+\frac{1}{2} y \leq 20\) mifano hali.

    1. Grafu usawa.
    2. Orodha ya ufumbuzi wa tatu kwa usawa\(2x+\frac{1}{2} y \leq 20\) ambapo wote wawili\(x\) na\(y\) ni namba nzima.
    Jibu

    1.
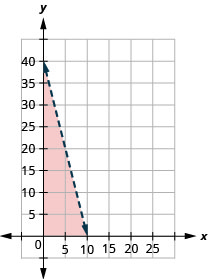
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x- huendesha kutoka 0 hadi 20 na y-axis huendesha kutoka 0 hadi 30. Mstari wa 2 x pamoja na nusu y sawa na 20 hupangwa kama mstari imara unaoenea kutoka juu kushoto kuelekea chini ya kulia. Kanda iliyo chini ya mstari ni kivuli.

    2. Majibu yatatofautiana.

    Mazoezi ya kuandika

    Zoezi\(\PageIndex{51}\)

    Lester anadhani kwamba suluhisho la usawa wowote na\(>\) ishara ni kanda juu ya mstari na suluhisho la usawa wowote na\(<\) ishara ni kanda chini ya mstari. Je, Lester ni sahihi? Eleza kwa nini au kwa nini.

    Zoezi\(\PageIndex{52}\)

    Eleza kwa nini katika baadhi ya grafu ya kutofautiana kwa mstari mstari wa mipaka ni imara lakini katika grafu nyingine hupigwa.

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    Hii ni meza ambayo ina safu nne na nguzo nne. Katika mstari wa kwanza, ambayo ni mstari wa kichwa, seli zinasoma kutoka kushoto kwenda kulia: “Ninaweza...,” “kwa ujasiri,” “kwa msaada fulani,” na “Hakuna-siipati!” Safu ya kwanza chini ya “Naweza...” inasoma “kuthibitisha ufumbuzi wa kutofautiana katika vigezo viwili,”, “kutambua uhusiano kati ya ufumbuzi wa usawa na grafu yake,” na “usawa wa mstari wa grafu.” Wengine wa seli ni tupu.

    b Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?