4.7: Grafu ya kutofautiana kwa mstari

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Thibitisha ufumbuzi wa kutofautiana katika vigezo viwili
• Kutambua uhusiano kati ya ufumbuzi wa usawa na grafu yake
• Graph usawa linear

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Tatua:$4x+3>23.$
   Ikiwa umekosa tatizo hili, kagua Zoezi 2.7.22.
2. Tafsiri kutoka algebra hadi Kiingereza:$x<5.$
   Ikiwa umekosa tatizo hili, kagua Zoezi 1.3.1.
3. Tathmini$3x−2y$ wakati$x=1, \, y=−2.$
   Kama amekosa tatizo hili, mapitio Zoezi 1.5.28.

Thibitisha Ufumbuzi wa Usawa katika Vigezo viwili

Tumejifunza jinsi ya kutatua kutofautiana katika kutofautiana moja. Sasa, tutaangalia usawa katika vigezo viwili. Ukosefu wa usawa katika vigezo viwili vina programu nyingi. Ikiwa unakimbia biashara, kwa mfano, ungependa mapato yako yawe makubwa kuliko gharama zako-ili biashara yako itafanya faida.

USAWA WA MSTARI

Ukosefu wa usawa wa mstari ni usawa ambao unaweza kuandikwa katika mojawapo ya fomu zifuatazo:

$$A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber$$

wapi$A$ na$B$ si wote sifuri.

Je! Unakumbuka kwamba usawa na kutofautiana moja ulikuwa na ufumbuzi wengi? Suluhisho la kukosekana$x>3$ kwa usawa ni idadi yoyote kubwa kuliko$3$. Sisi ilionyesha hii kwenye mstari idadi na shading katika mstari idadi na haki ya$3$, na kuweka mabano wazi katika$3$. Angalia Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$

Vile vile, kutofautiana katika vigezo viwili vina ufumbuzi wengi. Jozi yoyote iliyoamriwa$(x, y)$ ambayo inafanya usawa kweli wakati sisi badala katika maadili ni suluhisho la usawa.

Suluhisho la usawa wa mstari

Jozi zilizoamriwa$(x, y)$ ni suluhisho la usawa wa mstari ikiwa usawa ni kweli wakati sisi badala ya maadili ya$x$ na$y$.

Zoezi$\PageIndex{1}$

Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana$y>x+4$:

1. $(0,0)$
2. $(1,6)$
3. $(2,6)$
4. $(−5,−15)$
5. $(−8,12)$

Jibu

1.

$(0,0)$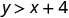
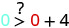
Kurahisisha.	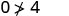	Hivyo,$(0,0)$ si ufumbuzi wa$y>x+4$.

2.

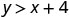
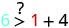
$(1,6)$
Kurahisisha.	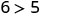	Hivyo,$(1,6)$ ni suluhisho la$y>x+4$.

3.

$(2,6)$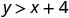
Kurahisisha.	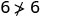	Hivyo,$(2,6)$ si ufumbuzi wa$y>x+4$.

4.

$(−5,−15)$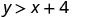
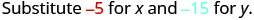
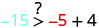
Kurahisisha.	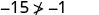	Hivyo,$(−5,−15)$ si ufumbuzi wa$y>x+4$.

5.

(-8,12)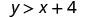
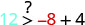
Kurahisisha.	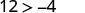	Hivyo,$(−8,12)$ ni suluhisho la$y>x+4$.

Zoezi$\PageIndex{2}$

Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana$y>x−3$:

1. $(0,0)$
2. $(4,9)$
3. $(−2,1)$
4. $(−5,−3)$
5. $(5,1)$

Jibu

1. ndiyo
2. ndiyo
3. ndiyo
4. ndiyo
5. hapana

Zoezi$\PageIndex{3}$

Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana$y<x+1$:

1. $(0,0)$
2. $(8,6)$
3. $(−2,−1)$
4. $(3,4)$
5. $(−1,−4)$

Jibu

1. ndiyo
2. ndiyo
3. hapana
4. hapana
5. ndiyo

Tambua Uhusiano Kati ya Ufumbuzi wa Usawa na Grafu yake

Sasa, tutaangalia jinsi ufumbuzi wa kutofautiana unahusiana na grafu yake.

Hebu fikiria juu ya mstari wa nambari katika Kielelezo$\PageIndex{1}$ tena. Hatua hiyo$x=3$ ilitenganisha mstari wa namba hiyo katika sehemu mbili. Upande mmoja wa$3$ ni namba zote chini ya$3$. Upande wa pili wa namba$3$ zote ni kubwa kuliko$3$. Angalia Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$

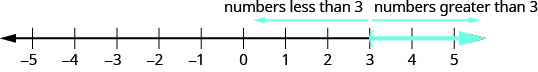
ufumbuzi wa$x>3$ ni sehemu kivuli ya mstari namba na haki ya$x=3$.

Vile vile, mstari$y=x+4$ hutenganisha ndege katika mikoa miwili. Kwa upande mmoja wa mstari ni pointi na$y<x+4$. Kwa upande mwingine wa mstari ni pointi na$y>x+4$. Tunaita mstari mstari$y=x+4$ wa mipaka.

MSTARI WA MIPAKA

Mstari na equation$Ax+By=C$ ni mstari wa mipaka unaotenganisha eneo ambapo$Ax+By>C$ kutoka kanda ambapo$Ax+By<C$.

Kwa usawa katika variable moja, mwisho wa mwisho unaonyeshwa kwa mabano au bracket kulingana na kama aa ni pamoja na katika suluhisho:

Vile vile, kwa usawa katika vigezo viwili, mstari wa mipaka unaonyeshwa kwa mstari imara au uliopigwa ili kuonyesha kama mstari umejumuishwa katika suluhisho. Hii ni muhtasari katika Jedwali$\PageIndex{1}$.

Jedwali$\PageIndex{1}$

$Ax+By<C$	$Ax+By\leq C$
$Ax+By>C$	$Ax+By\geq C$
Mstari wa mipaka haujumuishwa katika suluhisho.	Mstari wa mipaka umejumuishwa katika suluhisho.
Mstari wa mipaka umepigwa.	Mstari wa mipaka ni imara.

Sasa, hebu tuangalie kile tulichopata katika Zoezi$\PageIndex{1}$. Tutaanza kwa kuchora mstari$y=x+4$, na kisha tutaweza njama pointi tano tulizopimwa. Angalia Kielelezo$\PageIndex{3}$.

Kielelezo$\PageIndex{3}$

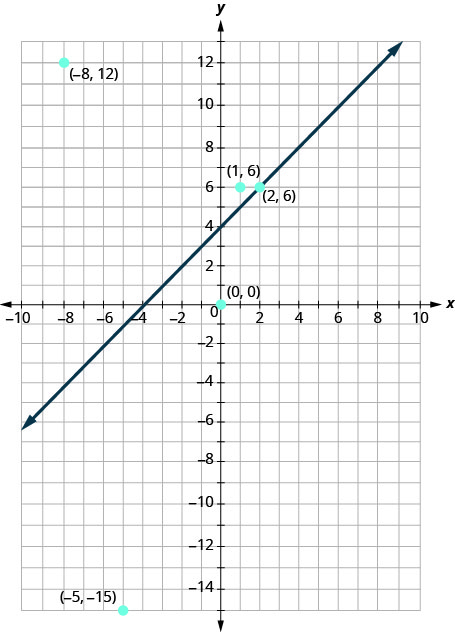
Katika Zoezi$\PageIndex{1}$ tuligundua kwamba baadhi ya pointi walikuwa ufumbuzi wa usawa$y>x+4$ na baadhi walikuwa si.

Ni ipi kati ya pointi tulizopanga ni ufumbuzi wa kutofautiana$y>x+4$? pointi$(1,6)$ na$(−8,12)$ ni ufumbuzi wa kukosekana kwa usawa$y>x+4$. Kumbuka kwamba wote wawili ni upande mmoja wa mstari wa mipaka$y=x+4$.

pointi mbili$(0,0)$ na$(−5,−15)$ ni upande wa pili wa mstari wa mipaka$y=x+4$, na wao si ufumbuzi wa usawa$y>x+4$. Kwa pointi hizo mbili,$y<x+4$.

Nini kuhusu hatua$(2,6)$? Kwa sababu$6=2+4$, hatua ni suluhisho la equation$y=x+4$. Hivyo hatua$(2,6)$ ni juu ya mstari wa mipaka.

Hebu tuchukue hatua nyingine upande wa kushoto wa mstari wa mipaka na ujaribu ikiwa ni suluhisho la kutofautiana$y>x+4$. Hatua inaonekana$(0,10)$ wazi kuwa upande wa kushoto wa mstari wa mipaka, siyo hivyo? Je, ni suluhisho la kukosekana kwa usawa?

$$\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}$$

Hatua yoyote unayochagua upande wa kushoto wa mstari wa mipaka ni suluhisho la usawa$y>x+4$. Vipengele vyote upande wa kushoto ni ufumbuzi.

Vile vile, pointi zote upande wa kulia wa mstari wa mipaka$(−5,−15)$, upande$(0,0)$ na, sio ufumbuzi$y>x+4$. Angalia Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$

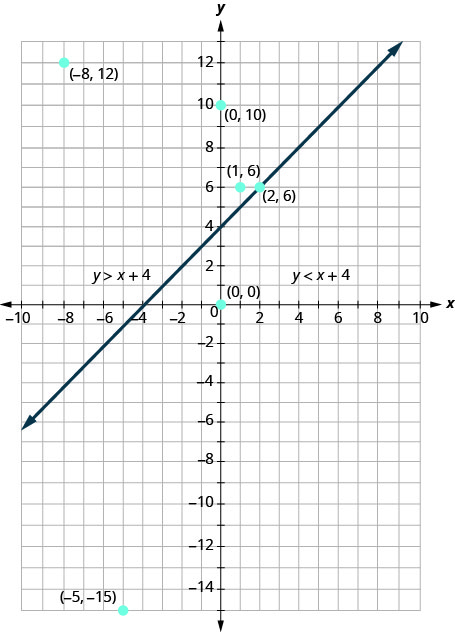
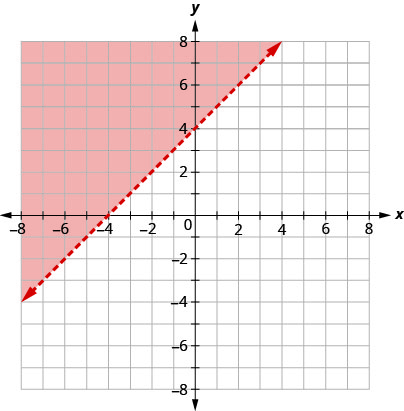
Grafu ya usawa$y>x+4$ inavyoonekana katika Kielelezo$\PageIndex{5}$ hapa chini. Mstari$y=x+4$ hugawanya ndege katika mikoa miwili. Upande wa kivuli unaonyesha ufumbuzi wa usawa$y>x+4$.

Pointi kwenye mstari wa mipaka$y=x+4$, wale ambapo, sio ufumbuzi wa usawa$y>x+4$, hivyo mstari yenyewe sio sehemu ya suluhisho. Tunaonyesha kwamba kwa kufanya mstari ulipungua, sio imara.

Kielelezo$\PageIndex{5}$: Grafu ya usawa y>x+4.

Zoezi$\PageIndex{4}$

Mstari wa mipaka umeonyeshwa ni$y=2x−1$. Andika usawa unaoonyeshwa na grafu.

Jibu

Mstari$y=2x−1$ ni mstari wa mipaka. Kwa upande mmoja wa mstari ni pointi$y>2x−1$ na upande wa pili wa mstari ni pointi na$y<2x−1$.

Hebu tujaribu hatua$(0,0)$ na tuone ni usawa gani unaoelezea upande wake wa mstari wa mipaka.

Katika$(0,0)$, ambayo kukosekana kwa usawa ni kweli:

$$\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}$$

Kwa kuwa$y>2x−1$ ni kweli, upande wa mstari na$(0,0)$, ni suluhisho. Eneo la kivuli linaonyesha ufumbuzi wa usawa$y>2x−1$.

Kwa kuwa mstari wa mipaka umewekwa na mstari imara, usawa unajumuisha ishara sawa.

Grafu inaonyesha usawa$y\geq 2x−1$.

Tunaweza kutumia hatua yoyote kama hatua ya mtihani, mradi si kwenye mstari. Kwa nini tulichagua$(0,0)$? Kwa sababu ni rahisi kutathmini. Unaweza kutaka kuchukua hatua upande wa pili wa mstari wa mpaka na kuangalia kwamba$y<2x−1$.

Zoezi$\PageIndex{5}$

Andika usawa unaoonyeshwa na grafu na mstari wa mipaka$y=−2x+3$.

Jibu

$y\geq −2x+3$

Zoezi$\PageIndex{6}$

Andika usawa unaoonyeshwa na grafu na mstari wa mipaka$y=\frac{1}{2}x−4$.

Jibu

$y \leq \frac{1}{2}x - 4$

Zoezi$\PageIndex{7}$

Mstari wa mipaka umeonyeshwa ni$2x+3y=6$. Andika usawa unaoonyeshwa na grafu.

Jibu

Mstari$2x+3y=6$ ni mstari wa mipaka. Kwa upande mmoja wa mstari ni pointi$2x+3y>6$ na upande wa pili wa mstari ni pointi na$2x+3y<6$.

Hebu tujaribu hatua$(0,0)$ na tuone ni usawa gani unaoelezea upande wake wa mstari wa mipaka.

Katika$(0,0)$, ambayo kukosekana kwa usawa ni kweli:

$$\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}$$

Hivyo upande na$(0,0)$ ni upande ambapo$2x+3y<6$.

(Unaweza kutaka kuchukua hatua upande wa pili wa mstari wa mpaka na kuangalia kwamba$2x+3y>6$.)

Kwa kuwa mstari wa mipaka umewekwa kama mstari uliopigwa, usawa haujumuishi ishara sawa.

Grafu inaonyesha suluhisho la kutofautiana$2x+3y<6$.

Zoezi$\PageIndex{8}$

Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka$x−4y=8$.

Jibu

$x-4 y \leq 8$

Zoezi$\PageIndex{9}$

Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka$3x−y=6$.

Jibu

$3 x-y \leq 6$

Graph Linear kutofautiana

Sasa, tuko tayari kuweka hii yote pamoja kwa usawa graph linear.

Zoezi$\PageIndex{10}$: How to Graph Linear Inequalities

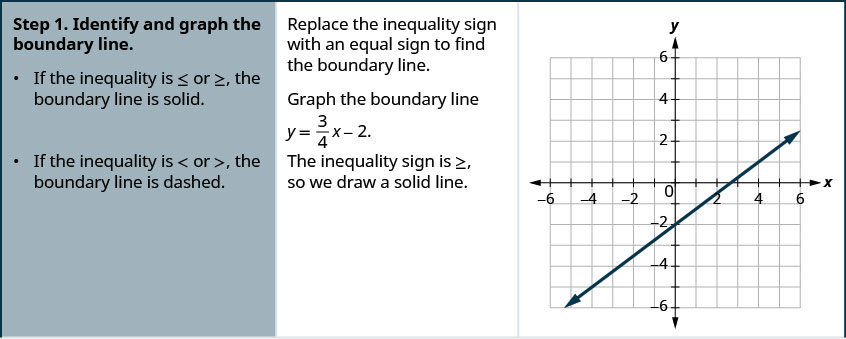
Grafu usawa wa mstari$y \geq \frac{3}{4} x-2$.

Jibu

Zoezi$\PageIndex{11}$

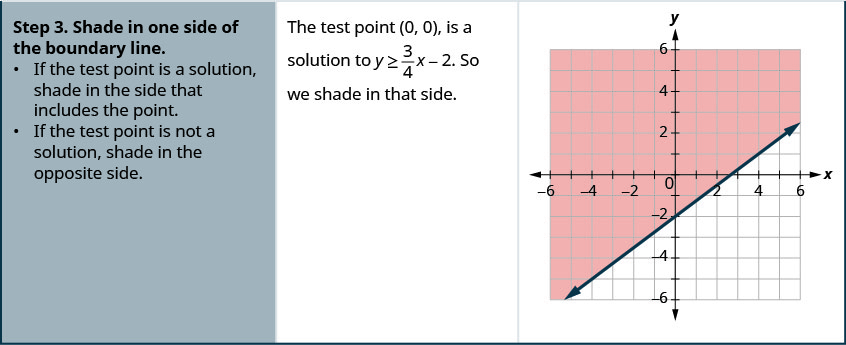
Grafu usawa wa mstari$y \geq \frac{5}{2} x-4$.

Jibu

Zoezi$\PageIndex{12}$

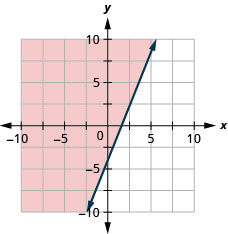
Grafu usawa wa mstari$y<\frac{2}{3} x-5$.

Jibu

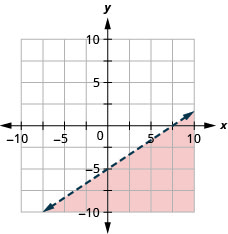
Hatua tunazochukua ili kuweka usawa wa mstari ni muhtasari hapa.

GRAFU USAWA WA MSTARI.

1. Tambua na graph mstari wa mipaka.
   • Ikiwa usawa ni$≤$ au$≥$, mstari wa mipaka ni imara.
   • Ikiwa usawa ni$<$ au$>$, mstari wa mipaka umepigwa.
2. Mtihani hatua ambayo si kwenye mstari wa mipaka. Je, ni suluhisho la kukosekana kwa usawa?
3. Kivuli upande mmoja wa mstari wa mipaka.
   • Ikiwa hatua ya mtihani ni suluhisho, kivuli upande unaojumuisha uhakika.
   • Ikiwa hatua ya mtihani sio suluhisho, kivuli upande wa pili.

Zoezi$\PageIndex{13}$

Grafu usawa wa mstari$x−2y<5$.

Jibu

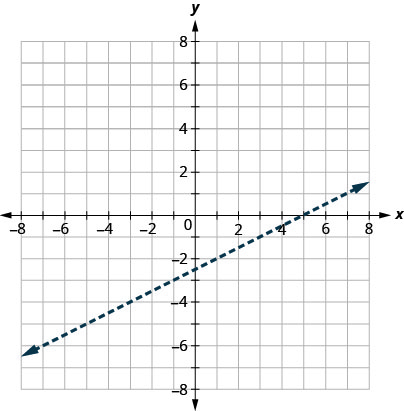
Kwanza tunapiga mstari wa mipaka$x−2y=5$. Ukosefu wa usawa ni$<$ hivyo sisi kuteka line dashed.

Kisha sisi mtihani uhakika. Tutaweza kutumia$(0,0)$ tena kwa sababu ni rahisi kutathmini na si kwenye mstari wa mipaka.

Je$(0,0)$ ufumbuzi wa$x−2y<5$?

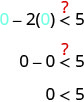
uhakika$(0,0)$ ni ufumbuzi wa$x−2y<5$, hivyo sisi kivuli katika upande huo wa mstari wa mipaka.

Zoezi$\PageIndex{14}$

Grafu usawa wa mstari$2x−3y\leq 6$.

Jibu

Zoezi$\PageIndex{15}$

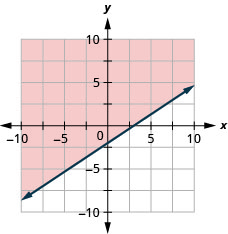
Grafu usawa wa mstari$2x−y>3$.

Jibu

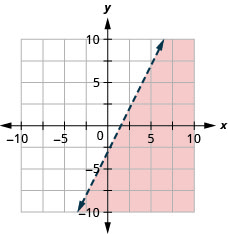
Nini kama mstari wa mipaka unapita kupitia asili? Kisha sisi si kuwa na uwezo wa kutumia$(0,0)$ kama hatua ya mtihani. Hakuna tatizo-tutaweza tu kuchagua baadhi ya hatua nyingine ambayo si juu ya mstari wa mpaka.

Zoezi$\PageIndex{16}$

Grafu usawa wa mstari$y\leq −4x$.

Jibu

Kwanza tunapiga mstari wa mipaka$y=−4x$. Ni katika mteremka-intercept fomu, na$m=−4$ na$b=0$. Ukosefu wa usawa ni$≤$ hivyo tunapata mstari imara.

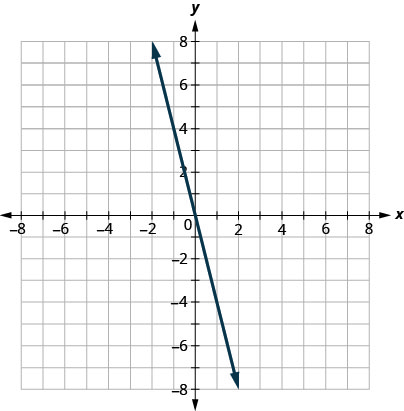
Sasa, tunahitaji hatua ya mtihani. Tunaweza kuona kwamba hatua$(1,0)$ si kwenye mstari wa mipaka.

Je$(1,0)$ ufumbuzi wa$y≤−4x$?

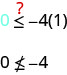
Hatua$(1,0)$ sio suluhisho$y≤−4x$, kwa hiyo sisi kivuli upande wa pili wa mstari wa mipaka. Angalia Kielelezo$\PageIndex{6}$.

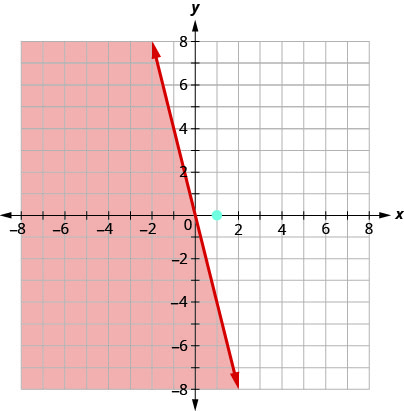
Kielelezo$\PageIndex{6}$

Zoezi$\PageIndex{17}$

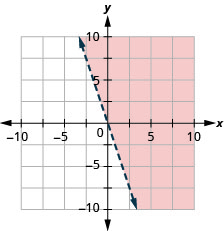
Grafu usawa wa mstari$y>−3x$.

Jibu

Zoezi$\PageIndex{18}$

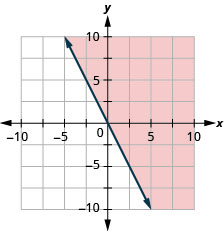
Grafu usawa wa mstari$y\geq −2x$.

Jibu

Baadhi ya kutofautiana kwa mstari una variable moja tu. Wanaweza kuwa$x$ lakini hapana$y$, au$y$ lakini hapana$x$. Katika kesi hizi, mstari wa mipaka utakuwa mstari wa wima au usawa. Je, unakumbuka?

$\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}$

Zoezi$\PageIndex{19}$

Grafu usawa wa mstari$y>3$.

Jibu

Kwanza tunapiga mstari wa mipaka$y=3$. Ni mstari usio na usawa. Ukosefu wa usawa ni$>$ hivyo sisi kuteka line dashed.

Sisi mtihani uhakika$(0,0)$.

$$y>3 \\ 0\not>3$$

$(0,0)$si ufumbuzi wa$y>3$.

Kwa hiyo sisi kivuli upande usiojumuisha$(0,0)$.

Zoezi$\PageIndex{20}$

Grafu usawa wa mstari$y<5$.

Jibu

Zoezi$\PageIndex{21}$

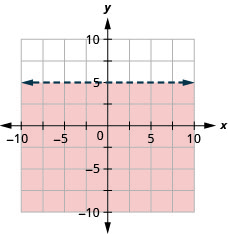
Grafu usawa wa mstari$y \leq-1$.

Jibu

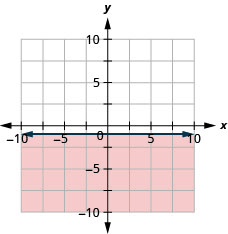
Dhana muhimu

• Kwa Grafu Usawa wa Mstari
  1. Tambua na graph mstari wa mipaka.
     Ikiwa usawa ni$≤$ au$≥$, mstari wa mipaka ni imara.
     Ikiwa usawa ni$<$ au$>$, mstari wa mipaka umepigwa.
  2. Mtihani hatua ambayo si kwenye mstari wa mipaka. Je, ni suluhisho la kukosekana kwa usawa?
  3. Kivuli upande mmoja wa mstari wa mipaka.
     Ikiwa hatua ya mtihani ni suluhisho, kivuli upande unaojumuisha uhakika.
     Ikiwa hatua ya mtihani sio suluhisho, kivuli upande wa pili.

faharasa

mstari wa mipaka

Mstari na equation$A x+B y=C$ ambayo hutenganisha kanda ambapo$A x+B y>C$ kutoka kanda ambapo$A x+B y<C$.

usawa wa mstari

Ukosefu wa usawa ambao unaweza kuandikwa katika mojawapo ya fomu zifuatazo:

$$A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C$$

wapi$A$ na$B$ si wote sifuri.

ufumbuzi wa usawa wa mstari

Jozi kuamuru$(x,\,y)$ ni suluhisho la usawa linear kukosekana kwa usawa ni kweli wakati sisi badala ya maadili ya$x$ na$y$.