4.5: Tumia Fomu ya mteremka—Kukataa ya Ulinganisho wa Mstari
- Page ID
- 177582
Mwishoni mwa sehemu hii, utaweza:
- Tambua uhusiano kati ya grafu na aina ya mteremka-intercept ya equation ya mstari
- Tambua mteremko na y-intercept fomu ya equation ya mstari
- Grafu mstari ukitumia mteremko wake na ukatie
- Chagua njia rahisi zaidi ya kuchora mstari
- Grafu na kutafsiri maombi ya mteremka-intercept
- Tumia mteremko kutambua mistari sambamba
- Tumia mteremko kutambua mistari ya perpendicular
Kabla ya kuanza, fanya jaribio hili la utayari.
- Ongeza:\(\frac{x}{4} + \frac{1}{4}\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.7.1. - Kupata kurudisha ya\(\frac{3}{7}\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.6.19. - Kutatua\(2x−3y=12\) kwa\(y\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 2.6.16.
Tambua Uhusiano Kati ya Grafu na Fomu ya Mteremo—Uingizaji wa Ulinganisho wa Mstari
Tuna graphed equations linear kwa pointi njama, kwa kutumia intercepts, kutambua mistari usawa na wima, na kutumia njia ya uhakika - mteremko. Mara baada ya kuona jinsi equation katika mteremko - intercept fomu na grafu yake ni kuhusiana, tutaweza kuwa na njia moja zaidi tunaweza kutumia kwa mistari graph.
Katika Ulinganisho wa Mstari wa Grafu katika Vigezo viwili, tulipiga mstari wa equation\(y=12x+3\) kwa pointi za kupanga. Angalia Kielelezo\(\PageIndex{1}\). Hebu tupate mteremko wa mstari huu.
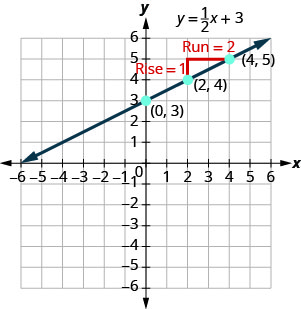
mistari nyekundu kutuonyesha kupanda ni\(1\) na kukimbia ni\(2\). Kuingiza katika formula ya mteremko:
\[\begin{aligned} m &=\frac{\text { rise }}{\text { rise }} \\ m &=\frac{1}{2} \end{aligned}\]
Je, ni\(y\) -intercept ya mstari? The\(y\) -intercept ni ambapo mstari unavuka\(y\) -axis, hivyo\(y\) -intercept ni\((0,3)\). Equation ya mstari huu ni:
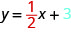
Angalia, mstari una:

Wakati equation ya mstari inatatuliwa\(y\), mgawo wa\(x\) -mrefu ni mteremko na muda wa mara kwa mara ni\(y\) -kuratibu ya\(y\) -intercept. Tunasema kwamba equation\(y=\frac{1}{2}x+3\) ni katika mteremka-intercept fomu.
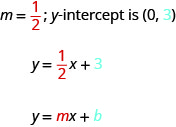
Aina ya mteremka-intercept ya equation ya mstari na mteremko mm na\(y\) -intercept,\((0,b)\) ni,
\[y=mx+b\]
Wakati mwingine fomu ya mteremka-intercept inaitwa “y -form.”
Tumia grafu ili kupata mteremko na\(y\) -intercept ya mstari,\(y=2x+1\).
Linganisha maadili haya kwa equation\(y=mx+b\).
- Jibu
-
Ili kupata mteremko wa mstari, tunahitaji kuchagua pointi mbili kwenye mstari. Tutatumia pointi\((0,1)\) na\((1,3)\).
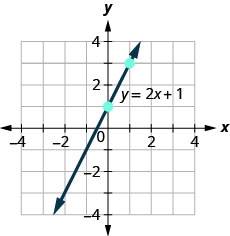
Kupata kupanda na kukimbia. 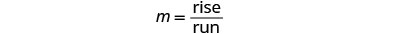
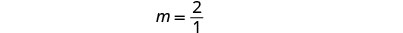
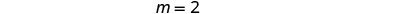
Pata\(y\) -intercept ya mstari. \(y\)-Intercept ni uhakika\((0, 1)\). 
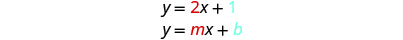
Mteremko ni sawa na mgawo wa\(x\) na\(y\) -kuratibu ya\(y\) -intercept ni sawa na muda wa mara kwa mara.
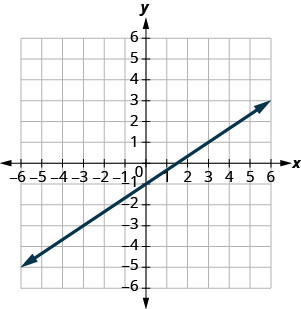
Tumia grafu ili kupata mteremko na\(y\) -intercept ya mstari\(y=\frac{2}{3}x−1\). Linganisha maadili haya kwa equation\(y=mx+b\).
- Jibu
-
mteremko\(m = \frac{2}{3}\) na\(y\) -intercept\((0,−1)\)
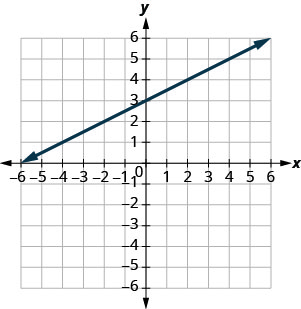
Tumia grafu ili kupata mteremko na\(y\) -intercept ya mstari\(y=\frac{1}{2}x+3\). Linganisha maadili haya kwa equation\(y=mx+b\).
- Jibu
-
mteremko\(m = \frac{1}{2}\) na\(y\) -intercept\((0,3)\)
Tambua Mteremko na\(y\) -Intercept Kutoka Equation ya Line
Katika Kuelewa[1] Slope ya Line, sisi graphed line kwa kutumia mteremko na uhakika. Wakati sisi ni kupewa equation katika mteremko - intercept fomu, tunaweza kutumia\(y\) -intercept kama uhakika, na kisha kuhesabu nje mteremko kutoka huko. Hebu tufanye mazoezi ya kutafuta maadili ya mteremko na\(y\) -intercept kutoka kwa usawa wa mstari.
Tambua mteremko na\(y\) -intercept ya mstari na equation\(y=−3x+5\).
- Jibu
-
Sisi kulinganisha equation yetu kwa mteremka-intercept fomu ya equation.
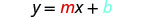
Andika equation ya mstari. 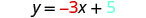
Tambua mteremko. 
Tambua\(y\) -intercept. 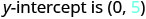
Tambua mteremko na\(y\) -intercept ya mstari\(y=\frac{2}{5}x−1\).
- Jibu
-
\(\frac{2}{5}\); (0, -1)
Tambua mteremko na\(y\) -intercept ya mstari\(y=−\frac{4}{3}x+1\).
- Jibu
-
\(-\frac{4}{3}\); (0,1)
Wakati equation ya mstari si kutolewa katika mteremka-intercept fomu, hatua yetu ya kwanza itakuwa kutatua equation kwa\(y\).
Tambua mteremko na\(y\) -intercept ya mstari na equation\(x+2y=6\).
- Jibu
-
Equation hii si katika mteremka-intercept fomu. Ili kulinganisha na mteremko - intercept fomu ni lazima kwanza kutatua equation kwa\(y\).
Kutatua kwa\(y\). \(x+2y=6\) Ondoa x kutoka kila upande. 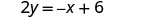
Gawanya pande zote mbili na\(2\). 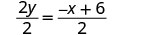
Kurahisisha. 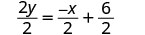
(Kumbuka:\(\frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}\)) Kurahisisha. 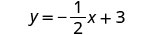
Andika mteremko - intercept fomu ya equation ya mstari. 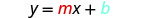
Andika equation ya mstari. 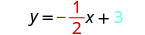
Tambua mteremko. 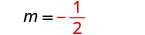
Tambua\(y\) -intercept. 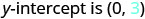
Tambua mteremko na\(y\) -intercept ya mstari\(x+4y=8\).
- Jibu
-
\(-\frac{1}{4}\);( 0,2)
Tambua mteremko na\(y\) -intercept ya mstari\(3x+2y=12\).
- Jibu
-
\(-\frac{2}{3}\);( 0,6)
Grafu Line Kutumia mteremko wake na Kukataa
Sasa kwa kuwa tunajua jinsi ya kupata mteremko na\(y\) -intercept ya mstari kutoka equation yake, tunaweza grafu mstari kwa kupanga\(y\) -intercept na kisha kutumia mteremko kupata hatua nyingine.
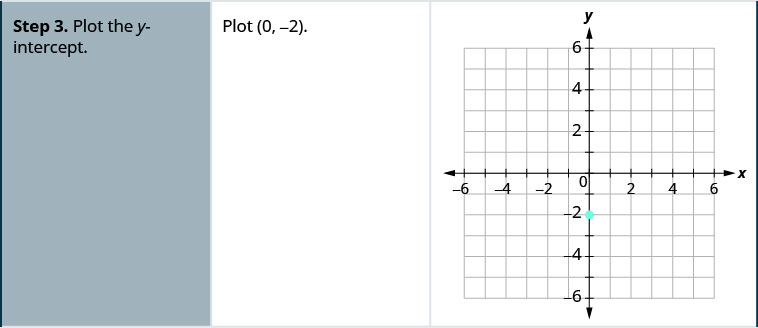
Grafu mstari wa equation kwa\(y=4x−2\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-



Grafu mstari wa equation kwa\(y=4x+1\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
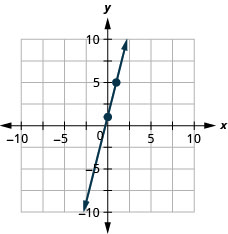
Grafu mstari wa equation kwa\(y=2x−3\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
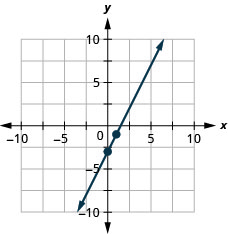
- Pata fomu ya kuingilia mteremko wa equation ya mstari.
- Tambua mteremko na\(y\) -intercept.
- Plot\(y\) -intercept.
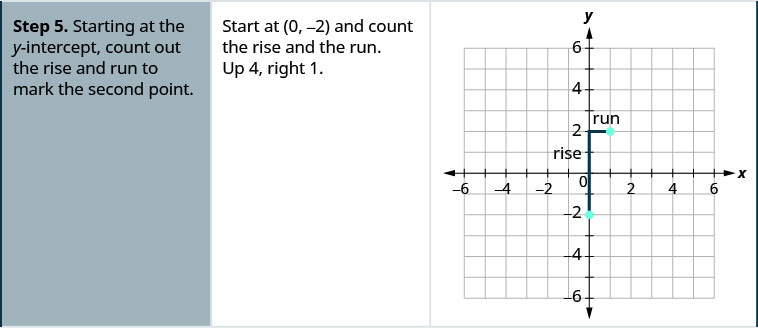
- Tumia formula\(\frac{\text{rise}}{\text{run}}\) ya mteremko kutambua kupanda na kukimbia.
- Kuanzia saa\(y\) -intercept, kuhesabu kupanda na kukimbia ili alama ya pili.
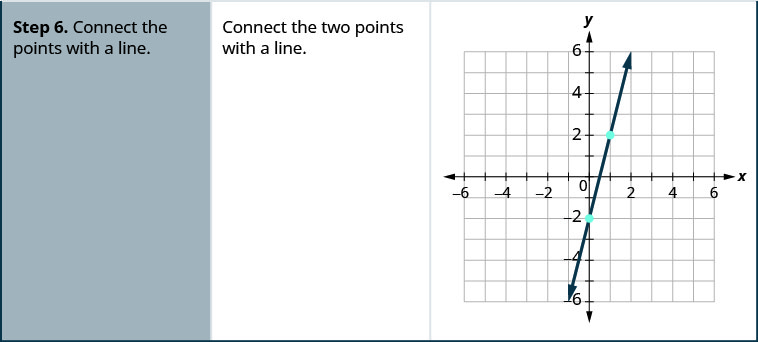
- Unganisha pointi kwa mstari.
Grafu mstari wa equation kwa\(y=−x+4\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
angalia.\(y=mx+b\) equation ni katika mteremka-intercept fomu. \(y=−x+4\) Tambua mteremko na\(y\) -intercept. \(m=−1\) \(y\)-kukatiza ni\((0, 4)\) Plot\(y\) -intercept. Angalia grafu hapa chini. Tambua kupanda na kukimbia. \(m = \frac{-1}{1}\) Kuhesabu kupanda na kukimbia alama ya pili. kupanda\(−1\), kukimbia\(1\) Chora mstari. 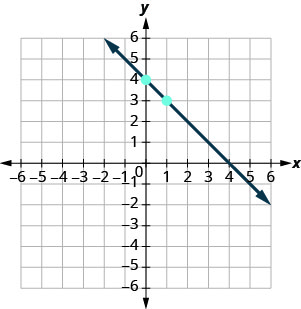
Kuangalia kazi yako, unaweza kupata hatua nyingine kwenye mstari na uhakikishe kuwa ni suluhisho la equation. Katika grafu tunaona mstari unaendelea\((4, 0)\). - \(\begin{array}{l}{y=-x+4} \\ {0\stackrel{?}{=}-4+4} \\ {0=0\checkmark}\end{array}\)
Grafu mstari wa equation kwa\(y=−x−3\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
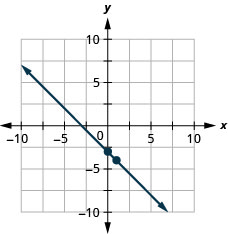
Grafu mstari wa equation kwa\(y=−x−1\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
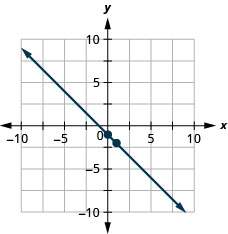
Grafu mstari wa equation kwa\(y=−\frac{2}{3}x−3\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
\(y=mx+b\) equation ni katika mteremka-intercept fomu. \(y=−\frac{2}{3}x−3\) Tambua mteremko na\(y\) -intercept. \(m = -\frac{2}{3}\);\(y\) -kukatiza ni\((0, −3)\) Plot\(y\) -intercept. Angalia grafu hapa chini. Tambua kupanda na kukimbia. Kuhesabu kupanda na kukimbia alama ya pili. Chora mstari. 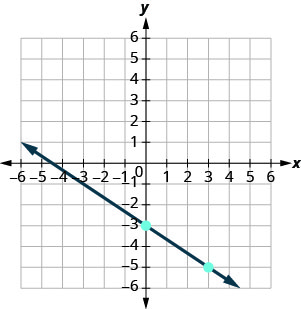
Grafu mstari wa equation kwa\(y=−\frac{5}{2}x+1\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
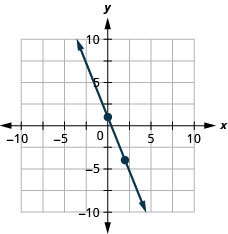
Grafu mstari wa equation kwa\(y=−\frac{3}{4}x−2\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
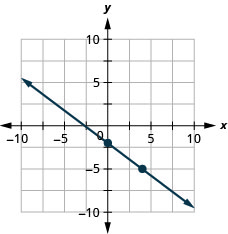
Grafu mstari wa equation kwa\(4x−3y=12\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
\(4x−3y=12\) Find mteremko - intercept fomu ya equation. \(−3y=−4x+12\) \(−\frac{3y}{3}=\frac{−4x+12}{−3}\) equation ni sasa katika mteremko - intercept fomu. \(y=\frac{4}{3}x−4\) Tambua mteremko na\(y\) -intercept. \(m=\frac{4}{3}\) \(y\)-kupinga ni\((0, −4)\) Plot\(y\) -intercept. Angalia grafu hapa chini. Tambua kupanda na kukimbia; kuhesabu kupanda na kukimbia alama ya pili. Chora mstari. 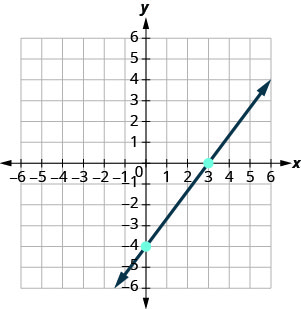
Grafu mstari wa equation kwa\(2x−y=6\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
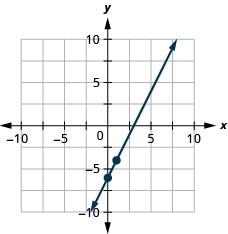
Grafu mstari wa equation kwa\(3x−2y=8\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
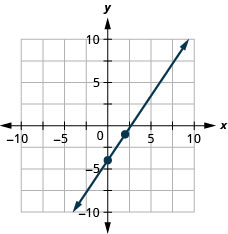
Tumetumia gridi ya taifa\(x\) na na\(y\) wote kwenda kutoka karibu\(−10\)\(10\) kwa milinganyo yote tumekuwa graphed hadi sasa. Sio equations zote za mstari zinaweza kupigwa kwenye gridi hii ndogo. Mara nyingi, hasa katika programu na data halisi ya ulimwengu, tutahitaji kupanua shaba kwa idadi kubwa au ndogo hasi.
Grafu mstari wa equation kwa\(y=0.2x+45\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
Tutaweza kutumia gridi ya taifa na shoka kwenda kutoka juu\(−80\) ya\(80\).
\(y=mx+b\) equation ni katika mteremka-intercept fomu. \(y=0.2x+45\) Tambua mteremko na\(y\) -intercept. \(m=0.2\) \(y\)Kukandamizaji ni\((0, 45)\) Plot\(y\) -intercept. Angalia grafu hapa chini. Kuhesabu kupanda na kukimbia alama ya pili. Mteremko ni\(m=0.2\); kwa fomu ya sehemu hii inamaanisha\(m=\frac{2}{10}\). Kutokana na ukubwa wa grafu yetu, itakuwa rahisi kutumia sehemu sawa\(m=\frac{10}{50}\). Chora mstari. 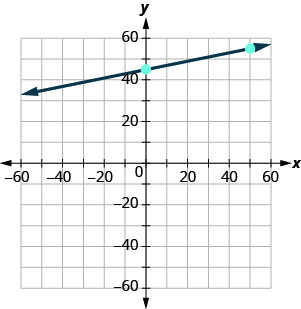
Grafu mstari wa equation kwa\(y=0.5x+25\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
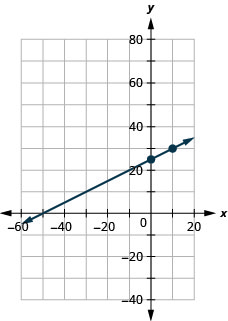
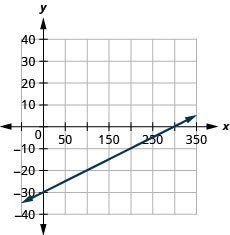
Grafu mstari wa equation kwa\(y=0.1x−30\) kutumia mteremko wake na\(y\) -intercept.
- Jibu
-
Sasa kwa kuwa tuna graphed mistari kwa kutumia mteremko na\(y\) -intercept, hebu muhtasari njia zote tuna kutumika kwa mistari grafu. Angalia Kielelezo\(\PageIndex{2}\).

Chagua Njia rahisi zaidi ya Grafu ya Mstari
Sasa kwa kuwa tumeona mbinu kadhaa tunaweza kutumia kwa mistari graph, jinsi gani tunajua ambayo njia ya kutumia kwa equation kupewa?
Wakati tunaweza njama pointi, kutumia mteremko - intercept fomu, au kupata intercepts kwa equation yoyote, kama sisi kutambua njia rahisi zaidi kwa graph aina fulani ya equation, kazi yetu itakuwa rahisi. Kwa ujumla, pointi za kupanga njama sio njia bora zaidi ya kuchora mstari. Tuliona mbinu bora katika sehemu 4.3, 4.4, na mapema katika sehemu hii. Hebu tuangalie mifumo fulani ili kusaidia kuamua njia rahisi zaidi ya kuchora mstari.
Hapa ni milinganyo sita sisi graphed katika sura hii, na njia sisi kutumika graph kila mmoja wao.
\[\begin{array}{lll}{\text{#1}}&{\text {Equation }} & {\text { Method }} \\ {\text{#2}}&{x=2} & {\text { Vertical line }} \\ {\text{#3}}&{y=4} & {\text { Hortical line }} \\ {\text{#4}}&{-x+2 y=6} & {\text { Intercepts }} \\ {\text{#5}}&{4 x-3 y=12} & {\text { Intercepts }} \\ {\text{#6}}&{y=4 x-2} & {\text { Slope-intercept }} \\{\text{#7}}& {y=-x+4} & {\text { Slope-intercept }}\end{array}\]
Ulinganifu #1 na #2 kila mmoja na variable moja tu. Kumbuka, katika equations ya fomu hii thamani ya variable moja ni mara kwa mara; haitegemei thamani ya variable nyingine. Ulinganisho wa fomu hii una grafu ambazo ni mistari ya wima au ya usawa.
Katika equations #3 na #4, wote wawili\(x\) na\(y\) ni upande mmoja wa equation. Hizi milinganyo miwili ni ya fomu\(Ax+By=C\). Sisi badala ya\(y=0\) kupata\(x\) -intercept na\(x=0\) kupata\(y\) -intercept, na kisha kupatikana hatua ya tatu kwa kuchagua thamani nyingine kwa\(x\) au\(y\).
Ulinganifu #5 na #6 vimeandikwa katika fomu ya mteremka-intercept. Baada ya kutambua mteremko na\(y\) -intercept kutoka equation sisi kutumika yao kwa graph line.
Hii inasababisha mkakati wafuatayo.
Fikiria fomu ya equation.
- Ikiwa ina variable moja tu, ni mstari wa wima au usawa.
- \(x=a\)ni mstari wa wima unaopitia\(x\) -axis saa\(a\).
- \(y=b\)ni mstari usio na usawa unaopitia\(y\) -axis saa\(b\).
- Ikiwa\(y\) imetengwa upande mmoja wa equation, kwa fomu\(y=mx+b\), grafu kwa kutumia mteremko na\(y\) -intercept.
- Tambua mteremko na\(y\) -intercept na kisha grafu.
- Ikiwa equation ni ya fomu\(Ax+By=C\), pata vipindi.
- Kupata\(x\) - na\(y\) -intercepts, hatua ya tatu, na kisha grafu.
Tambua njia rahisi zaidi ya grafu kila mstari.
- \(y=−6\)
- \(5x−3y=15\)
- \(x=7\)
- \(y=\frac{2}{5}x−1\).
- Jibu
-
1. \(y=−6\)
Equation hii ina variable moja tu,\(y\). Grafu yake ni mstari usio na usawa unaovuka\(y\) -axis saa\(−6\).2. \(5x−3y=15\)
Equation hii ni ya fomu\(Ax+By=C\). Njia rahisi zaidi ya grafu itakuwa kupata intercepts na hatua moja zaidi.3. \(x=7\)
Kuna variable moja tu,\(x\). Grafu ni mstari wa wima unaovuka\(x\) -axis saa\(7\).4. \(y=\frac{2}{5}x−1\)
Kwa kuwa equation hii iko katika\(y=mx+b\) fomu, itakuwa rahisi kupiga mstari huu kwa kutumia mteremko na\(y\) -intercept.
Kuamua njia rahisi zaidi ya grafu kila mstari:
- \(3x+2y=12\)
- \(y=4\)
- \(y=\frac{1}{5}x−4\)
- \(x=−7\)
- Jibu
-
- ingilia kati
- mstari usio na usawa
- mteremka-kukatiza
- mstari wa wima
Kuamua njia rahisi zaidi ya grafu kila mstari:
- \(x=6\)
- \(y=−\frac{3}{4}x+1\)
- \(y=−8\)
- \(4x−3y=−1\)
- Jibu
-
- mstari wa wima
- mteremka-kukatiza
- mstari usio na usawa
- ingilia kati
Grafu na Kutafsiri Matumizi ya mteremko — Intercept
Maombi mengi ya ulimwengu halisi yanatokana na equations linear. Sisi kuangalia maombi chache hapa hivyo unaweza kuona jinsi equations imeandikwa katika mteremka-intercept fomu yanahusiana na hali halisi ya dunia.
Kawaida wakati equation linear mifano hali halisi ya dunia, barua tofauti hutumiwa kwa vigezo, badala ya\(x\) na\(y\). Majina ya kutofautiana yanatukumbusha kiasi gani kinachopimwa.
Equation\(F=\frac{9}{5}C+32\) hutumiwa kubadili joto,\(C\), kwa kiwango cha Celsius hadi joto,\(F\), kwa kiwango cha Fahrenheit.
- Kupata joto Fahrenheit kwa joto Celsius ya\(0\).
- Kupata joto Fahrenheit kwa joto Celsius ya\(20\).
- Tafsiri mteremko na\(F\) -intercept ya equation.
- Grafu equation.
- Jibu
-
1. \(\begin{array}{ll}{\text { Find the Fahrenheit temperature for a Celsius temperature of } 0 .} & {F=\frac{9}{5} C+32} \\ {\text { Find } F \text { when } C=0 .} & {F=\frac{9}{5}(0)+32} \\ {\text { Simplify. }} & {F=32}\end{array}\)
2. \ kuanza {array} {ll} {\ maandishi {Pata joto la Fahrenheit kwa joto la Celsius la} 20.} & {F=\ frac {9} {5} C+32}\\ {\ maandishi {Kupata} F\ maandishi {wakati} C=20.} & {F=\ frac {9} {5} (20) +32}\\ {\ Nakala {Kurahisisha.}} & {F = 36+32}\\ {\ Nakala {Kurahisisha.}} & {F=68}\ mwisho {safu}
3. Tafsiri mteremko na\(F\) -intercept ya equation.
Hata kama equation hii inatumia\(F\) na\(C\), bado ni katika mteremka-intercept fomu.
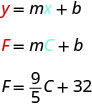
Mteremko\(\frac{9}{5}\), ina maana kwamba joto Fahrenheit (\(F\)) huongeza\(9\) digrii wakati joto Celsius (\(C\)) huongeza\(5\) digrii.
\(F\)-Intercept ina maana kwamba wakati joto liko\(0°\) kwenye kiwango cha Celsius, ni\(32°\) juu ya kiwango cha Fahrenheit.
4. Grafu equation.
Tutahitaji kutumia kiwango kikubwa kuliko kawaida yetu. Anza saa\(F\) -intercept\((0,32)\) kisha kuhesabu kupanda kwa\(9\) na kukimbia\(5\) kwa kupata hatua ya pili. Angalia Kielelezo\(\PageIndex{3}\).
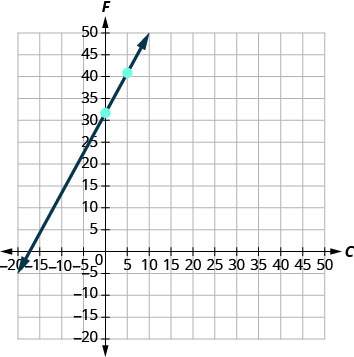
Kielelezo\(\PageIndex{3}\)
Equation\(h=2s+50\) hutumiwa kukadiria urefu wa mwanamke kwa inchi,\(h\), kulingana na ukubwa wa kiatu chake,\(s\).
- Tathmini urefu wa mtoto ambaye amevaa ukubwa wa kiatu cha wanawake\(0\).
- Tathmini urefu wa mwanamke mwenye ukubwa wa kiatu\(8\).
- Tafsiri mteremko na\(h\) -intercept ya equation.
- Grafu equation.
- Jibu
-
- \(50\)inchi
- \(66\)inchi
- mteremko\(2\),, ina maana kwamba urefu\(h\),, kuongezeka kwa\(2\) inchi wakati ukubwa kiatu\(s\), kuongezeka kwa\(1\). \(h\)-Intercept ina maana kwamba wakati ukubwa wa kiatu ni\(0\), urefu ni\(50\) inchi.
Equation\(T=\frac{1}{4}n+40\) hutumiwa kukadiria joto katika digrii Fahrenheit,\(T\), kulingana na idadi ya chirps kriketi\(n\),, katika dakika moja.
- Tathmini joto wakati hakuna chirps.
- Tathmini joto wakati idadi ya chirps katika dakika moja ni\(100\).
- Tafsiri mteremko na\(T\) -intercept ya equation.
- Grafu equation.
- Jibu
-
- \(40\)digrii
- \(65\)digrii
- mteremko\(\frac{1}{4}\),, ina maana kwamba joto Fahrenheit (\(F\)) kuongezeka\(1\) shahada wakati idadi ya chirps\(n\), kuongezeka kwa\(4\). \(T\)-Intercept ina maana kwamba wakati idadi ya chirps ni\(0\), joto ni\(40°\).
Gharama ya kuendesha biashara ya aina fulani ina vipengele viwili-gharama za kudumu na gharama ya kutofautiana. Gharama ya kudumu daima ni sawa bila kujali vitengo vingi vinavyotengenezwa. Hii ni gharama ya kodi, bima, vifaa, matangazo, na vitu vingine ambavyo vinapaswa kulipwa mara kwa mara. Gharama ya kutofautiana inategemea idadi ya vitengo zinazozalishwa. Ni kwa ajili ya vifaa na kazi zinazohitajika kuzalisha kila kitu.
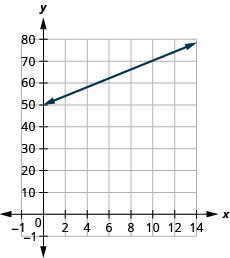
Stella ina biashara ya nyumbani kuuza pizzas gourmet. equation\(C=4p+25\) mifano uhusiano kati ya gharama yake ya kila wiki\(C\),, katika dola na idadi ya pizzas\(p\), kwamba yeye anauza.
- Kupata gharama Stella kwa wiki wakati yeye anauza hakuna pizzas.
- Kupata gharama kwa wiki wakati yeye anauza\(15\) pizzas.
- Tafsiri mteremko na\(C\) -intercept ya equation.
- Grafu equation.
- Jibu
-
1. Kupata gharama Stella kwa wiki wakati yeye anauza hakuna pizzas. 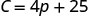
Pata\(C\) lini\(p=0\). 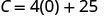
Kurahisisha. 
Stella ya gharama za kudumu ni\($25\) wakati yeye anauza hakuna pizzas. 2. Kupata gharama kwa wiki wakati yeye anauza\(15\) pizzas. 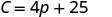
Pata\(C\) lini\(p=15\). 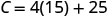
Kurahisisha. 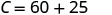

Gharama za Stella ni\($85\) wakati anauza\(15\) pizzas. 3. Tafsiri mteremko na\(C\) -intercept ya equation. 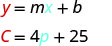
Mteremko,\(4\), ina maana kwamba gharama huongezeka\($4\) kwa kila pizza Stella anauza. The\(C\) -intercept ina maana kwamba hata wakati Stella anauza pizzas hakuna, gharama zake kwa wiki ni\($25\). 4. Grafu equation. Tutahitaji kutumia kiwango kikubwa kuliko kawaida yetu. Anza saa\(C\) -intercept\((0, 25)\) kisha kuhesabu kupanda kwa\(4\) na kukimbia\(1\) kwa kupata hatua ya pili. 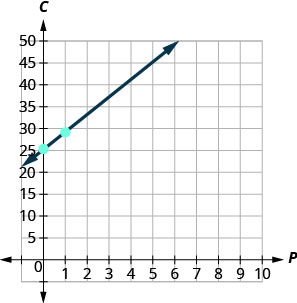
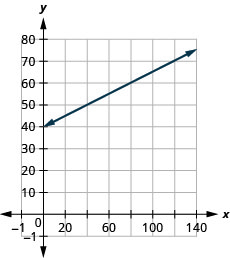
Sam anatoa van utoaji. equation\(C=0.5m+60\) mifano uhusiano kati ya gharama yake ya kila wiki\(C\),, katika dola na idadi ya maili,\(m\), kwamba anatoa.
- Kupata gharama Sam kwa wiki wakati anatoa\(0\) maili.
- Kupata gharama kwa wiki wakati anatoa\(250\) maili.
- Tafsiri mteremko na\(C\) -intercept ya equation.
- Grafu equation.
- Jibu
-
- \($60\)
- \($185\)
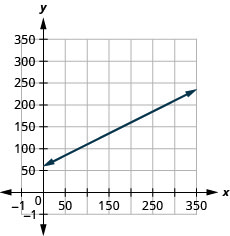
- mteremko,\(0.5\), ina maana kwamba gharama ya kila wiki\(C\),, kuongezeka kwa\($0.50\) wakati idadi ya maili inaendeshwa\(n\), kuongezeka kwa\(1\). The\(C\) -intercept ina maana kwamba wakati idadi ya maili inaendeshwa ni\(0\), gharama ya kila wiki ni\($60\).
Loreen ina biashara ya calligraphy. equation\(C=1.8n+35\) mifano uhusiano kati ya gharama yake ya kila wiki\(C\),, katika dola na idadi ya mialiko ya harusi\(n\),, kwamba anaandika.
- Kupata gharama Loreen kwa wiki wakati yeye anaandika hakuna mialiko.
- Kupata gharama kwa wiki wakati yeye anaandika\(75\) mialiko.
- Tafsiri mteremko na\(C\) -intercept ya equation.
- Grafu equation.
- Jibu
-
- \($35\)
- \($170\)
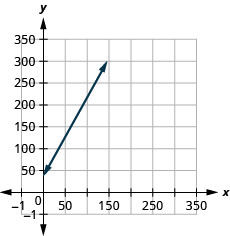
- mteremko,\(1.8\), ina maana kwamba gharama ya kila wiki\(C\),, kuongezeka kwa\($1.80\) wakati idadi ya mialiko\(n\), kuongezeka kwa\(1.80\). \(C\)-Intercept ina maana kwamba wakati idadi ya mialiko ni\(0\), gharama ya kila wiki ni\($35\).
Tumia Materemko Kutambua Mistari Sambamba
Mteremko wa mstari unaonyesha jinsi mstari ulivyo mwinuko na ikiwa unaongezeka au huanguka kama tunavyoisoma kutoka kushoto kwenda kulia. Mstari miwili ambayo ina mteremko huo huitwa mistari sambamba. Mstari sambamba kamwe intersect.

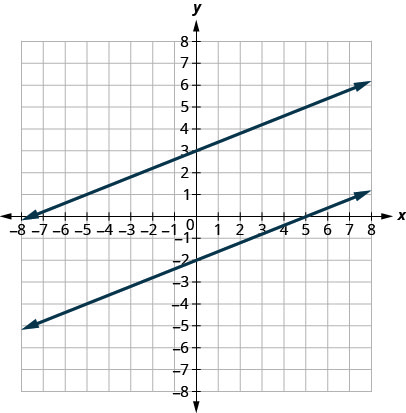
Nini kuhusu mistari ya wima? Mteremko wa mstari wa wima haujafafanuliwa, hivyo mistari ya wima haifai katika ufafanuzi hapo juu. Tunasema kwamba mistari ya wima ambayo ina tofauti\(x\) -intercepts ni sambamba. Angalia Kielelezo\(\PageIndex{5}\).
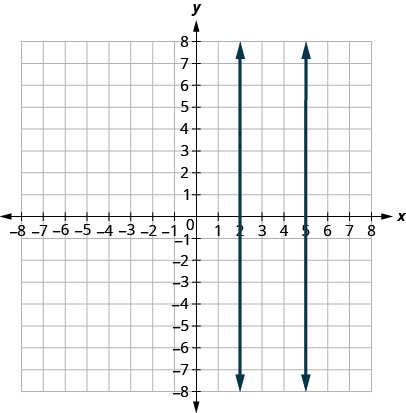
Mstari sambamba ni mistari katika ndege moja ambayo haipatikani.
- Mstari sambamba una mteremko sawa na tofauti\(y\) -intercepts.
- Ikiwa\(m_{1}\) na\(m_{2}\) ni mteremko wa mistari miwili inayofanana basi\(m_{1} = m_{2}\).
- Mstari wa wima sambamba una tofauti\(x\) -intercepts.
Hebu tuchapishe equations\(y=−2x+3\) na\(2x+y=−1\) kwenye gridi hiyo. equation kwanza ni tayari katika mteremka-intercept fomu:\(y=−2x+3\). Sisi kutatua equation ya pili kwa\(y\):
\[\begin{aligned} 2x+y &=-1 \\ y &=-2x-1 \end{aligned}\]
Grafu mistari.
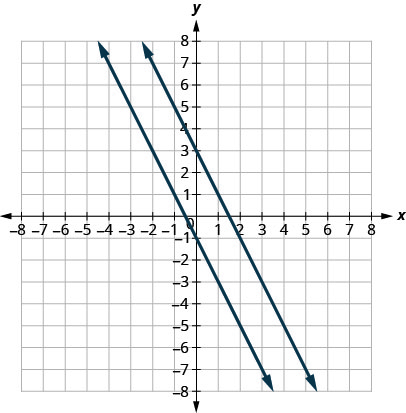
Angalia mistari kuangalia sambamba. Je, ni mteremko wa kila mstari? Ni nini\(y\) -intercept ya kila mstari?
\[\begin{array}{lll} {y} & {=m x+b} & {y=m x+b} \\ {y} & {=-2 x+3} & {y=-2 x-1} \\ {m} & {=-2} & {m=-2}\\ {b} & {=3,(0,3)} & {b=-1,(0,-1)}\end{array}\]
Miteremko ya mistari ni sawa na\(y\) -intercept ya kila mstari ni tofauti. Hivyo tunajua mistari hii ni sambamba.
Tangu mistari sambamba na mteremko huo na tofauti\(y\) -intercepts, sasa tunaweza tu kuangalia aina mteremko - intercept ya milinganyo ya mistari na kuamua kama mistari ni sambamba.
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(3x−2y=6\) na\(y = \frac{3}{2}x + 1\) ni sambamba.
- Jibu
-
\(\begin{array} {lrll} {\text { Solve the first equation for } y .} &{ 3 x-2 y} &{=} &{6}\\{} & {\frac{-2 y}{-2}} &{ =}&{-3 x+6 }\\ {} &{\frac{-2 y}{-2}}&{ =}&{\frac{-3 x+6}{-2}} \\ {} & {y }&{=}&{\frac{3}{2} x-3} \end{array}\)
equation ni sasa katika mteremko - intercept fomu.
Equation ya mstari wa pili ni tayari katika mteremka-intercept fomu.
Tambua mteremko na\(y\) -intercept ya mistari yote.
\(\begin{array}{lll}{y=\frac{3}{2} x+1} & {} & {y=\frac{3}{2} x-3} \\ {y=m x+b} & {} & {y=m x+b}\\ {m=\frac{3}{2}} & {} & {m=\frac{3}{2}} \\ {y\text{-intercept is }(0, 1)} & {} & {y\text{-intercept is }(0, −3)} \end{array}\)
Mstari una mteremko sawa na tofauti\(y\) -intercepts na hivyo ni sambamba. Unaweza kutaka graph mistari ili kuthibitisha kama ni sambamba.
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(2x+5y=5\) na\(y=−\frac{2}{5}x−4\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(4x−3y=6\) na\(y=\frac{4}{3}x−1\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=−4\) na\(y=3\) ni sambamba.
- Jibu
-
\(\begin{array}{llll}{\text{Write each equation in slope-intercept form.}} &{y=-4} & {\text { and }} &{ y=3} \\ {\text{Since there is no }x\text{ term we write }0x.} &{y=0 x-4} & {} &{y=0 x+3} \\ {\text{Identify the slope and }y\text{-intercept of both lines.}} &{y=m x+b} &{} & {y=m x+b} \\ {} &{m=0} &{} & {m=0} \\{} & {y\text {-intercept is }(0,4)} &{} & {y \text {-intercept is }(0,3)}\end{array}\)
Mstari una mteremko sawa na tofauti\(y\) -intercepts na hivyo ni sambamba.
Kuna njia nyingine unaweza kuangalia mfano huu. Ikiwa unatambua mara moja kutoka kwa usawa kwamba hizi ni mistari ya usawa, unajua mteremko wao ni wote wawili\(0\). Kwa kuwa mistari ya usawa huvuka\(y\) -axis saa\(y=−4\) na saa\(y=3\), tunajua\(y\) -intercepts ni\((0,−4)\) na\((0,3)\). Mstari una mteremko sawa na tofauti\(y\) -intercepts na hivyo ni sambamba.
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=8\) na\(y=−6\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=1\) na\(y=−5\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(x=−2\) na\(x=−5\) ni sambamba.
- Jibu
-
\[x=-2 \text { and } x=-5\]
Kwa kuwa hakuna\(y\), equations haiwezi kuweka katika mteremka-intercept fomu. Lakini tunawatambua kama equations ya mistari ya wima. Yao\(x\) -intercepts ni\(−2\) na\(−5\). Kwa kuwa\(x\) -intercepts yao ni tofauti, mistari ya wima ni sawa.
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(x=1\) na\(x=−5\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(x=8\) na\(x=−6\) ni sambamba.
- Jibu
-
sambamba
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=2x−3\) na\(−6x+3y=−9\) ni sambamba. Unaweza kutaka graph mistari hii, pia, kuona nini wao kuangalia kama.
- Jibu
-
\(\begin{array} {llll} {\text { The first equation is already in slope-intercept form. }} & {y=2x-3}&{}&{} \\ \\ {\text { Solve the second equation for } y} & {-6x+3y} &{=}&{-9} \\{} & {3y}&{=}&{6x-9} \\ {}&{\frac{3y}{3} }&{=}&{\frac{6x-9}{3}} \\{} & {y}&{=}&{2x-3}\end{array}\)
Equation ya pili ni sasa katika mteremka-intercept fomu pia.
Tambua mteremko na\(y\) -intercept ya mistari yote.
\[\begin{array}{lll}{y=2x-3} &{} & {y=2x-3} \\ {y=mx+b} &{} & {y=mx+b} \\ {m=2} &{} & {m=2} \\ {\text{The }y\text{-intercept is }(0 ,−3)} &{} & {\text{The }y\text{-intercept is }(0 ,−3)} \end{array} \nonumber\]
Mstari una mteremko huo, lakini pia wana\(y\) -intercepts sawa. Equations yao inawakilisha mstari huo. Hao sambamba; wao ni mstari sawa.
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=−\frac{1}{2}x−1\) na\(x+2y=2\) ni sambamba.
- Jibu
-
si sambamba; mstari huo
Tumia mteremko na\(y\) -intercepts kuamua kama mistari\(y=\frac{3}{4}x−3\) na\(3x−4y=12\) ni sambamba.
- Jibu
-
si sambamba; mstari huo
Tumia Materemko ya Kutambua Mipangilio ya Per
Hebu tuangalie mistari ambayo equations ni\(y=\frac{1}{4}x−1\) na\(y=−4x+2\), inavyoonekana katika Kielelezo\(\PageIndex{5}\).
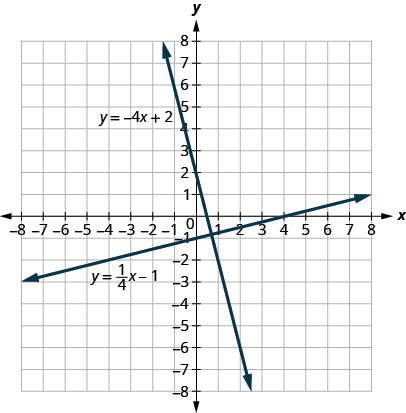
Mstari huu uongo katika ndege moja na kuingiliana katika pembe za kulia. Tunaita mistari hii perpendicular.
Unaona nini kuhusu mteremko wa mistari hii miwili? Tunaposoma kutoka kushoto kwenda kulia, mstari\(y=14x−1\) unaongezeka, hivyo mteremko wake ni chanya. Mstari\(y=−4x+2\) hupungua kutoka kushoto kwenda kulia, kwa hiyo una mteremko hasi. Je, ni busara kwako kwamba mteremko wa mistari miwili ya perpendicular itakuwa na ishara tofauti?
Ikiwa tunaangalia mteremko wa mstari wa kwanza,\(m_{1}=14\), na mteremko wa mstari wa pili\(m_{2}=−4\), tunaweza kuona kwamba wao ni usawa mbaya wa kila mmoja. Ikiwa tunawazidisha, bidhaa zao ni\(−1\).
\[\begin{array}{c}{m_{1} \cdot m_{2}} \\ {\frac{1}{4}(-4)} \\ {-1}\end{array}\]
Hii daima ni kweli kwa mistari perpendicular na inatuongoza kwa ufafanuzi huu.
Mstari wa perpendicular ni mistari katika ndege moja ambayo huunda angle sahihi.
Ikiwa m1 na m2 ni mteremko wa mistari miwili ya perpendicular, basi:
\[m_{1} \cdot m_{2}=-1 \text { and } m_{1}=\frac{-1}{m_{2}}\]
Mstari wa wima na mistari ya usawa ni daima perpendicular kwa kila mmoja.
Tulikuwa na uwezo wa kuangalia mteremko - intercept aina ya equations linear na kuamua kama au mistari walikuwa sambamba. Tunaweza kufanya kitu kimoja kwa mistari ya perpendicular.
Tunapata mteremka-intercept fomu ya equation, na kisha kuona kama mteremko ni requirals hasi. Ikiwa bidhaa ya mteremko ni\(−1\), mistari ni perpendicular. Mstari wa perpendicular inaweza kuwa sawa\(y\) -intercepts.
Tumia mteremko kuamua kama mistari,\(y=−5x−4\) na\(x−5y=5\) ni perpendicular.
- Jibu
-
Equation ya kwanza iko tayari katika mteremka-intercept fomu:\(\quad y=−5x−4\)
\(\begin{array} {llll} {\text{Solve the second equation for }y.} &{x-5y} &{=} &{5} \\{} &{-5 y} &{=} &{-x+5} \\ {} & {\frac{-5 y}{-5}} &{=} &{\frac{-x+5}{-5}} \\ {} &{y} &{=} &{\frac{1}{5} x-1} \end{array}\)Equation ya pili sasa iko katika fomu ya mteremka-intercept pia.
\(\begin{array} {lrllllll} {\text{Identify the slope of each line.}} &{y} &{=} &{-5 x-4} & {} &{y} &{=} &{\frac{1}{5} x-1} \\ {} &{y} &{=} &{m x+b} & {} &{y} &{=} &{m x+b}\\ {} &{m_{1}} &{=}&{-5} & {} &{m_{2}} &{=}&{\frac{1}{5}}\end{array}\)
Miteremko ni usawa mbaya wa kila mmoja, hivyo mistari ni perpendicular. Sisi kuangalia kwa kuzidisha mteremko,
\[\begin{array}{l}{m_{1} \cdot m_{2}} \\ {-5\left(\frac{1}{5}\right)} \\ {-1\checkmark}\end{array}\]
Tumia mteremko kuamua kama mistari\(y=−3x+2\) na\(x−3y=4\) ni perpendicular.
- Jibu
-
wima
Tumia mteremko kuamua kama mistari\(y=2x−5\) na\(x+2y=−6\) ni perpendicular.
- Jibu
-
wima
Tumia mteremko kuamua kama mistari,\(7x+2y=3\) na\(2x+7y=5\) ni perpendicular.
- Jibu
-
\(\begin{array}{lrlrl}{\text{Solve the equations for y.}} &{7 x+2 y} & {=3} & {2 x+7 y}&{=}&{5} \\{} & {2 y} & {=-7 x+3} & {7 y}&{=}&{-2 x+5} \\ {} &{\frac{2 y}{2}} & {=\frac{-7 x+3}{2} \quad} & {\frac{7 y}{7}}&{=}&{\frac{-2 x+5}{7}} \\ {} &{y} & {=-\frac{7}{2} x+\frac{3}{2}} &{y}&{=}&{\frac{-2}{7}x + \frac{5}{7}}\\ \\{\text{Identify the slope of each line.}} & {y}&{=m x+b} &{y}&{=}&{m x+b} \\{} & {m_{1}} & {=-\frac{7}{2} }&{ m_{2}}&{=}&{-\frac{2}{7}}\end{array}\)
Miteremko ni ya usawa wa kila mmoja, lakini wana ishara sawa. Kwa kuwa sio usawa mbaya, mistari haipatikani.
Tumia mteremko kuamua kama mistari\(5x+4y=1\) na\(4x+5y=3\) ni perpendicular.
- Jibu
-
si perpendicular
Tumia mteremko kuamua kama mistari\(2x−9y=3\) na\(9x−2y=1\) ni perpendicular.
- Jibu
-
si perpendicular
Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na grafu.
Dhana muhimu
- Aina ya mteremka-intercept ya equation ya mstari na mteremko mm na\(y\) -intercept,\((0,b)\) ni,\(y=mx+b\).
- Grafu Line Kutumia mteremko wake na\(y\) -Intercept
- Pata fomu ya kuingilia mteremko wa equation ya mstari.
- Tambua mteremko na\(y\) -intercept.
- Plot\(y\) -intercept.
- Tumia formula\(m = \dfrac{\text{rise}}{\text{run}}\) ya mteremko kutambua kupanda na kukimbia.
- Kuanzia saa\(y\) -intercept, kuhesabu kupanda na kukimbia ili alama ya pili.
- Unganisha pointi kwa mstari.
- Mkakati wa Kuchagua Njia rahisi zaidi ya Graph Line: Fikiria fomu ya equation.
- Ikiwa ina variable moja tu, ni mstari wa wima au usawa.
\(x = a\)ni mstari wa wima unaopitia\(x\) -axis katika.
\(y = b\) ni mstari usio na usawa unaopita kwa njia ya\(y\) -axis\(b\). - Ikiwa\(y\) imetengwa upande mmoja wa equation, kwa fomu\(y=mx+b\), grafu kwa kutumia mteremko na\(y\) -intercept.
Tambua mteremko na\(y\) -intercept na kisha grafu. - Ikiwa equation ni ya fomu\(Ax+By=C\), pata vipindi.
Kupata\(x\) - na\(y\) -intercepts, hatua ya tatu, na kisha grafu.
- Ikiwa ina variable moja tu, ni mstari wa wima au usawa.
- Mstari sambamba ni mistari katika ndege moja ambayo haipatikani.
- Mstari sambamba una mteremko sawa na tofauti\(y\) -intercepts.
- Ikiwa\(m_1\) na\(m_2\) ni mteremko wa mistari miwili inayofanana basi\(m_1 = m_2\).
- Mstari wa wima sambamba una tofauti\(x\) -intercepts.
- Mstari wa perpendicular ni mistari katika ndege moja ambayo huunda angle sahihi.
- Ikiwa\(m_1\) na\(m_2\) ni mteremko wa mistari miwili ya perpendicular, basi\(m_1\cdot m_2=−1\) na\(m_1=\frac{−1}{m_2}\).
- Mstari wa wima na mistari ya usawa ni daima perpendicular kwa kila mmoja.
faharasa
- mistari sambamba
- Mistari katika ndege moja ambayo haipatikani.
- mistari perpendicular
- Mistari katika ndege moja ambayo huunda angle sahihi.
- mteremka-intercept aina ya equation ya mstari
- Aina ya mteremka-intercept ya equation ya mstari na mteremko mm na\(y\) -intercept,\((0,b)\) ni,\(y=mx+b\).


