Skip to main content
Global

4.4E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    177611

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Tumia Geoboards kwa Model Slope

    Katika mazoezi yafuatayo, tafuta mteremko unaoelekezwa kwenye kila geoboard.

    Zoezi\(\PageIndex{1}\)

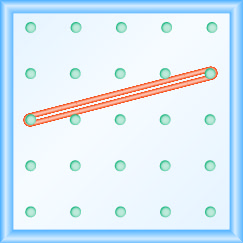
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 3 na nguruwe katika safu ya 5, mstari wa 2, na kutengeneza mstari.

    Jibu

    \(\frac{1}{4}\)

    Zoezi\(\PageIndex{2}\)

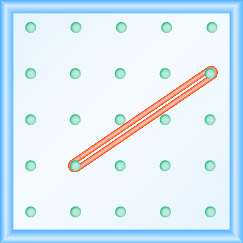
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 2, mstari wa 4 na nguruwe katika safu ya 5, mstari wa 2, na kutengeneza mstari.

    Zoezi\(\PageIndex{3}\)

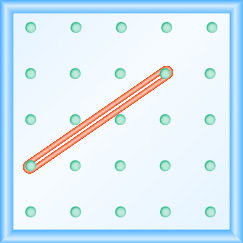
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 4 na nguruwe katika safu ya 4, mstari wa 2, na kutengeneza mstari.

    Jibu

    \(\frac{2}{3}\)

    Zoezi\(\PageIndex{4}\)

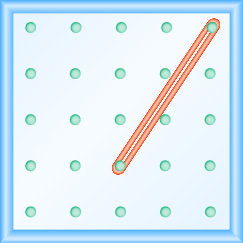
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 3, mstari wa 4 na nguruwe katika safu ya 5, mstari wa 1, kutengeneza mstari.

    Zoezi\(\PageIndex{5}\)

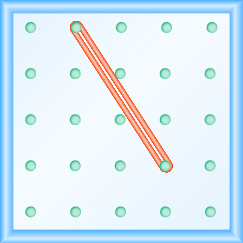
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 2, mstari wa 1 na nguruwe katika safu ya 4, mstari wa 4, na kutengeneza mstari.

    Jibu

    \(\frac{-3}{2}=-\frac{3}{2}\)

    Zoezi\(\PageIndex{6}\)

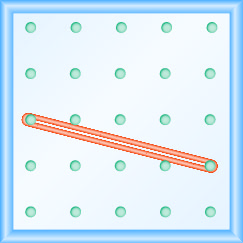
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 3 na nguruwe katika safu ya 5, mstari wa 4, na kutengeneza mstari.

    Zoezi\(\PageIndex{7}\)

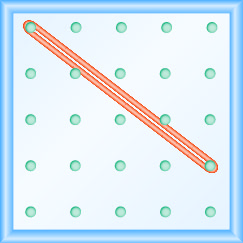
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 1 na nguruwe katika safu ya 5, mstari wa 4, na kutengeneza mstari.

    Jibu

    \(-\frac{2}{3}\)

    Zoezi\(\PageIndex{8}\)

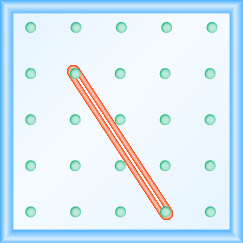
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 2, mstari wa 2 na nguruwe katika safu ya 4, mstari wa 5, kutengeneza mstari.

    Katika mazoezi yafuatayo, mfano kila mteremko. Chora picha ili kuonyesha matokeo yako.

    Zoezi\(\PageIndex{9}\)

    \(\frac{2}{3}\)

    Jibu

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 2, mstari wa 5 na nguruwe katika safu ya 5, mstari wa 3, na kutengeneza mstari.

    Zoezi\(\PageIndex{10}\)

    \(\frac{3}{4}\)

    Zoezi\(\PageIndex{11}\)

    \(\frac{1}{4}\)

    Jibu

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 4 na nguruwe katika safu ya 5, mstari wa 3, na kutengeneza mstari.

    Zoezi\(\PageIndex{12}\)

    \(\frac{4}{3}\)

    Zoezi\(\PageIndex{13}\)

    \(-\frac{1}{2}\)

    Jibu

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 4 na nguruwe katika safu ya 3, mstari wa 5, na kutengeneza mstari.

    Zoezi\(\PageIndex{14}\)

    \(-\frac{3}{4}\)

    Zoezi\(\PageIndex{15}\)

    \(-\frac{2}{3}\)

    Jibu

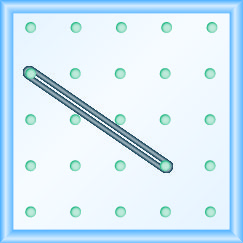
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 2 na nguruwe katika safu ya 4, mstari wa 4, na kutengeneza mstari.

    Zoezi\(\PageIndex{16}\)

    \(-\frac{3}{2}\)

    Tumia\(m=\frac{rise}{run}\) ili kupata Slope ya Line kutoka Grafu yake

    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari umeonyeshwa.

    Zoezi\(\PageIndex{17}\)

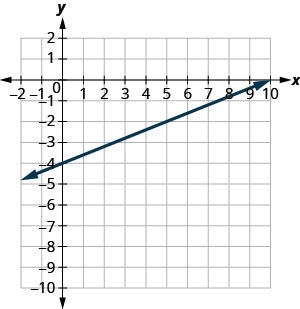
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unapita kupitia pointi (hasi 10, hasi 8), (0, hasi 4), na (10, 0).

    Jibu

    \(\frac{2}{5}\)

    Zoezi\(\PageIndex{18}\)

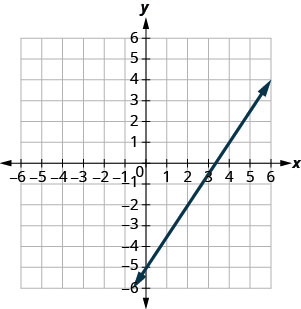
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 2, hasi 8) na (2, hasi 2).

    Zoezi\(\PageIndex{19}\)

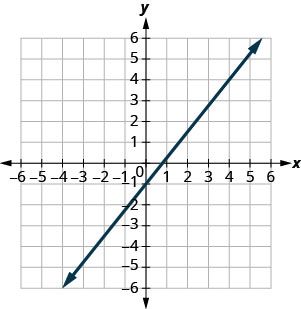
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 4, hasi 6) na (4, 4).

    Jibu

    \(\frac{5}{4}\)

    Zoezi\(\PageIndex{20}\)

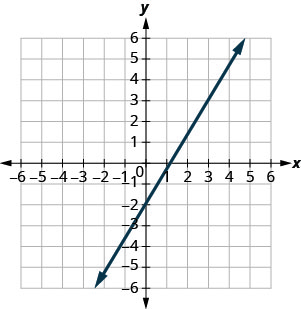
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unachukua mhimili wa y saa (0, hasi 2) na hupita kupitia hatua (3, 3).

    Zoezi\(\PageIndex{21}\)

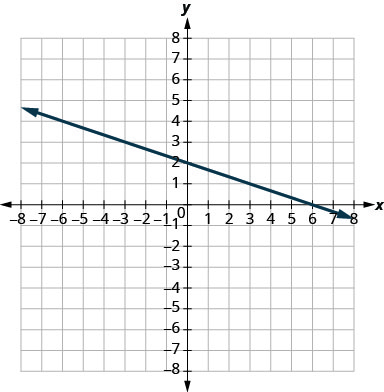
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 3, 3) na (3, 1).

    Jibu

    \(-\frac{1}{3}\)

    Zoezi\(\PageIndex{22}\)

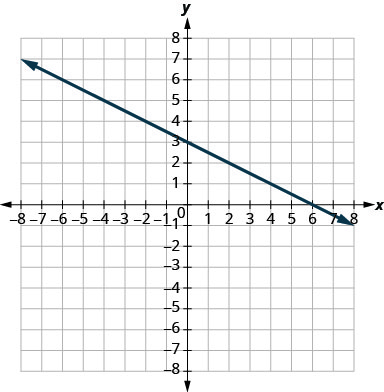
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 2, 4) na (2, 2).

    Zoezi\(\PageIndex{23}\)

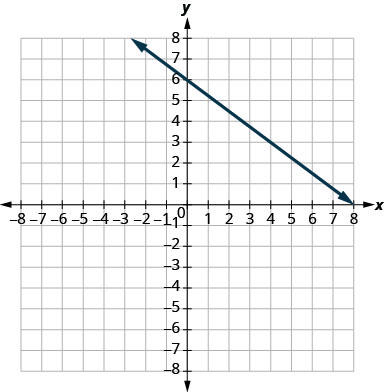
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unachukua mhimili wa y saa (0, 6) na hupita kupitia hatua (4, 3).

    Jibu

    \(-\frac{3}{4}\)

    Zoezi\(\PageIndex{24}\)

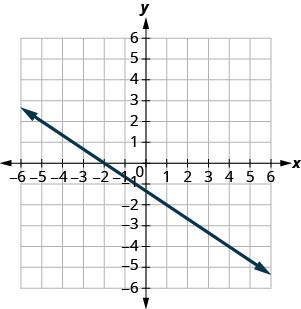
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia hatua (hasi 3, 1) na huchukua mhimili wa y saa (0, hasi 1).

    Zoezi\(\PageIndex{25}\)

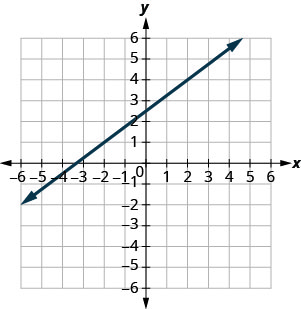
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 2, 1) na (2, 4).

    Jibu

    \(\frac{3}{4}\)

    Zoezi\(\PageIndex{26}\)

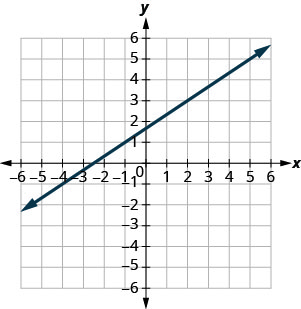
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 1, 1) na (2, 3).

    Zoezi\(\PageIndex{27}\)

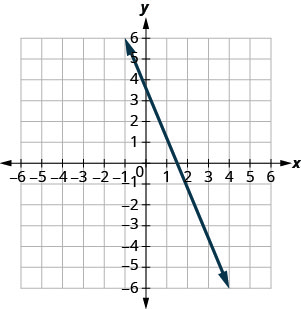
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 1, 6) na (1, 1).

    Jibu

    \(-\frac{5}{2}\)

    Zoezi\(\PageIndex{28}\)

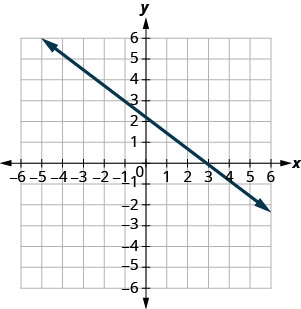
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia hatua (hasi 1, 3) na huchukua x-axis saa (3, 0).

    Zoezi\(\PageIndex{29}\)

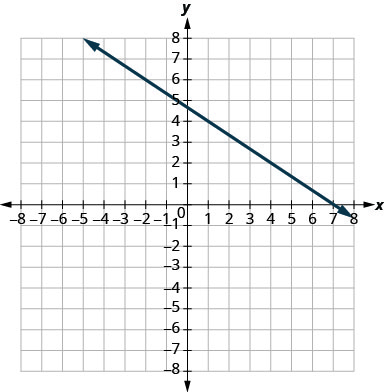
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 2, 6) na (1, 4).

    Jibu

    \(-\frac{2}{3}\)

    Zoezi\(\PageIndex{30}\)

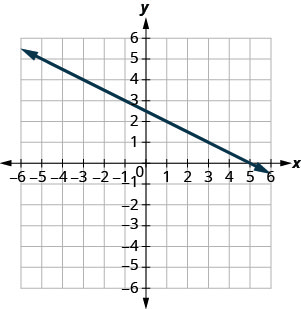
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unapita kupitia pointi (hasi 1, 3) na (1, 2).

    Zoezi\(\PageIndex{31}\)

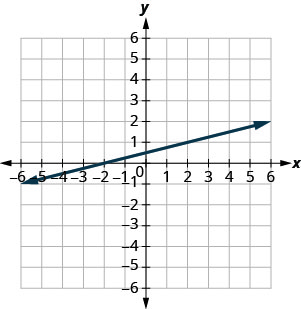
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unachukua x-axis saa (hasi 2, 0) na hupita kupitia hatua (2, 1).

    Jibu

    \(\frac{1}{4}\)

    Zoezi\(\PageIndex{32}\)

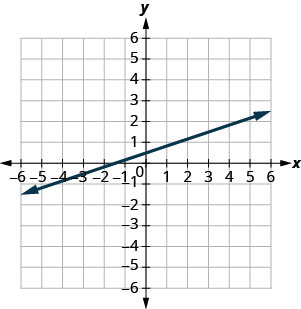
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unapita kupitia pointi (4, 2) na (7, 3).

    Pata mteremko wa Mistari ya Ulalo na Wima

    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.

    Zoezi\(\PageIndex{33}\)

    y=3

    Jibu

    0

    Zoezi\(\PageIndex{34}\)

    y=1

    Zoezi\(\PageIndex{35}\)

    x=4

    Jibu

    haijafafanuliwa

    Zoezi\(\PageIndex{36}\)

    x=2

    Zoezi\(\PageIndex{37}\)

    y=-1

    Jibu

    0

    Zoezi\(\PageIndex{38}\)

    y=1-3

    Zoezi\(\PageIndex{39}\)

    x=-5

    Jibu

    haijafafanuliwa

    Zoezi\(\PageIndex{40}\)

    x=-4

    Tumia Mfumo wa Slope ili kupata mteremko wa Mstari kati ya Pointi mbili

    Katika mazoezi yafuatayo, tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya kila jozi ya pointi.

    Zoezi\(\PageIndex{41}\)

    (1,4), (3,9)

    Jibu

    \(\frac{5}{2}\)

    Zoezi\(\PageIndex{42}\)

    (2,3), (5,7)

    Zoezi\(\PageIndex{43}\)

    (0,3), (4,6)

    Jibu

    \(\frac{3}{4}\)

    Zoezi\(\PageIndex{44}\)

    (0,1), (5,4)

    Zoezi\(\PageIndex{45}\)

    (2,5), (4,0)

    Jibu

    \(-\frac{5}{2}\)

    Zoezi\(\PageIndex{46}\)

    (3,6), (8,0)

    Zoezi\(\PageIndex{47}\)

    (-3,3), (4, -5)

    Jibu

    \(-\frac{8}{7}\)

    Zoezi\(\PageIndex{48}\)

    (-2,4), (3, -1)

    Zoezi\(\PageIndex{49}\)

    (-1, -2), (2,5)

    Jibu

    \(\frac{7}{3}\)

    Zoezi\(\PageIndex{50}\)

    (-2, -1), (6,5)

    Zoezi\(\PageIndex{51}\)

    (4, -5), (1, -1)

    Jibu

    -1

    Zoezi\(\PageIndex{52}\)

    (3, -6), (2, -2)

    Grafu Mstari Kutolewa Point na Slope

    Katika mazoezi yafuatayo, grafu kila mstari na hatua iliyotolewa na mteremko.

    Zoezi\(\PageIndex{53}\)

    \((1,-2) ; m=\frac{3}{4}\)

    Jibu

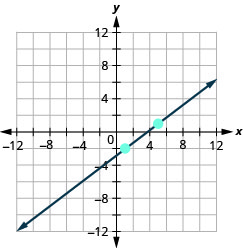
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (1, hasi 2) na (5, 1).

    Zoezi\(\PageIndex{54}\)

    \((1,-1) ; m=\frac{2}{3}\)

    Zoezi\(\PageIndex{55}\)

    \((2,5) ; m=-\frac{1}{3}\)

    Jibu

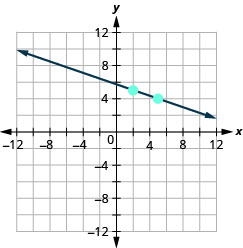
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (2, 5) na (5, 4).

    Zoezi\(\PageIndex{56}\)

    \((1,4) ; m=-\frac{1}{2}\)

    Zoezi\(\PageIndex{57}\)

    \((-3,4) ; m=-\frac{3}{2}\)

    Jibu

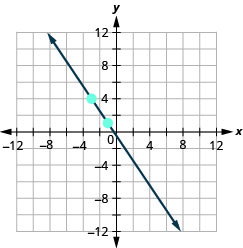
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (hasi 3, 4) na (hasi 1, 1).

    Zoezi\(\PageIndex{58}\)

    \((-2,5) ; m=-\frac{5}{4}\)

    Zoezi\(\PageIndex{59}\)

    \((-1,-4) ; m=\frac{4}{3}\)

    Jibu

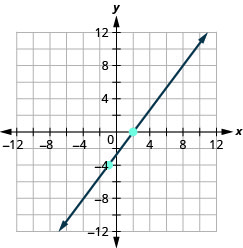
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (hasi 1, hasi 4) na huchukua x-axis saa (2, 0).

    Zoezi\(\PageIndex{60}\)

    \((-3,-5) ; m=\frac{3}{2}\)

    Zoezi\(\PageIndex{61}\)

    \(y\)-kukatiza\(3 ; m=-\frac{2}{5}\)

    Jibu

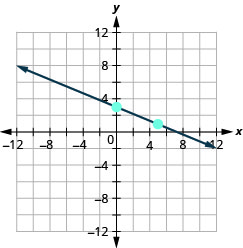
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unachukua mhimili wa y saa (0, 3) na hupita kupitia hatua (5, 1).

    Zoezi\(\PageIndex{62}\)

    \(y\)-kukatiza\(5 ; m=-\frac{4}{3}\)

    Zoezi\(\PageIndex{63}\)

    \(x\)-kukatiza\(-2 ; m=\frac{3}{4}\)

    Jibu

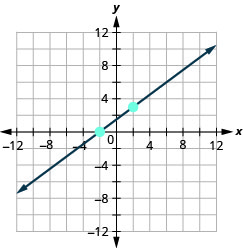
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unachukua x-axis saa (hasi 2, 0) na hupita kupitia hatua (2, 3).

    Zoezi\(\PageIndex{64}\)

    \(x\)-kukatiza\(-1 ; m=\frac{1}{5}\)

    Zoezi\(\PageIndex{65}\)

    \((-3,3) ; m=2\)

    Jibu

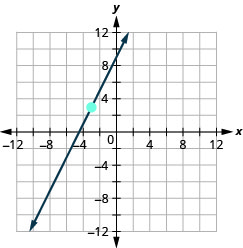
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (hasi 3, 3) na (hasi 2, 5).

    Zoezi\(\PageIndex{66}\)

    \((-4,2) ; m=4\)

    Zoezi\(\PageIndex{67}\)

    \((1,5) ; m=-3\)

    Jibu

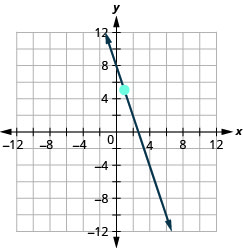
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (1, 5) na (2, 2).

    Zoezi\(\PageIndex{68}\)

    \((2,3) ; m=-1\)

    kila siku Math

    Zoezi\(\PageIndex{69}\)

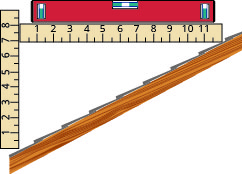
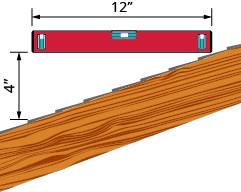
    Mteremko wa paa. Njia rahisi ya kuamua mteremko wa paa ni kuweka mwisho mmoja wa ngazi ya inchi 12 juu ya uso wa paa na kushikilia kiwango. Kisha kuchukua kipimo cha mkanda au mtawala na kupima kutoka mwisho mwingine wa ngazi hadi kwenye uso wa paa. Hii itakupa mteremko wa paa. Wajenzi, wakati mwingine, hutaja hii kama lami na kuiweka kama maana ya “x 12 lami”\(\frac{x}{12}\), ambapo x ni kipimo kutoka paa hadi ngazi-kupanda. Pia wakati mwingine alisema kama “x-in-12" lami.

    1. Je, ni mteremko wa paa katika picha hii?
    2. Je! Ni lami gani katika suala la ujenzi?
      Takwimu hii inaonyesha upande mmoja wa paa la mteremko wa nyumba. Kuongezeka kwa paa ni kinachoitwa “inchi 4" na kukimbia kwa paa ni kinachoitwa “inchi 12".
    Jibu
    1. \(\frac{1}{3}\)
    2. 4 12 lami au 4-in-12 lami
    Zoezi\(\PageIndex{70}\)

    Mteremko wa paa umeonyeshwa hapa unapimwa kwa kiwango cha “12” na mtawala. Je, ni mteremko wa paa hii?

    Takwimu hii inaonyesha upande mmoja wa paa la mteremko wa nyumba. Kuongezeka kwa paa kunapimwa na mtawala na kuonyeshwa kuwa inchi 7. Kukimbia kwa paa hupimwa kwa kiwango cha inchi kumi na mbili na kuonyeshwa kuwa inchi 12.

    Zoezi\(\PageIndex{71}\)

    Daraja la barabara. Barabara ya ndani ina daraja la 6%. Daraja la barabara ni mteremko wake ulioonyeshwa kama asilimia. Kupata mteremko wa barabara kama sehemu na kisha kurahisisha. Nini kupanda na kukimbia bila kutafakari mteremko huu au daraja?

    Jibu

    \(\frac{3}{50} ;\)kupanda\(=3,\) kukimbia\(=50\)

    Zoezi\(\PageIndex{72}\)

    Highway daraja. Barabara ya ndani inaongezeka miguu 2 kwa kila futi 50 za barabara kuu.

    1. Je, ni mteremko wa barabara kuu?
    2. Daraja la barabara kuu ni mteremko wake ulioonyeshwa kama asilimia. Je! Ni daraja gani la barabara hii?
    Zoezi\(\PageIndex{73}\)

    Njia ya magurudumu. Sheria za barabara za magurudumu zinahitaji kupanda kwa inchi 1-inch kwa kukimbia kwa inchi 12.

    1. Je, barabara lazima iwe kwa muda gani ili kuzingatia kupanda kwa inchi 24 hadi mlango?
    2. Unda mfano wa barabara hii.
    Jibu
    1. Inchi 288 (futi 24)
    2. Mifano zitatofautiana.
    Zoezi\(\PageIndex{74}\)

    Njia ya magurudumu. Kuongezeka kwa inchi 1 kwa kukimbia kwa inchi 16 hufanya iwe rahisi kwa mpanda farasi wa magurudumu kupaa njia panda.

    1. Muda gani lazima barabara iwe kwa urahisi kubeba kupanda kwa inchi 24 hadi mlango?
    2. Unda mfano wa barabara hii.

    Mazoezi ya kuandika

    Zoezi\(\PageIndex{75}\)

    Ishara ya mteremko inakuambia nini kuhusu mstari?

    Jibu

    Wakati mteremko ni namba nzuri mstari unaendelea kutoka kushoto kwenda kulia. Wakati mteremko ni namba hasi mstari unashuka kutoka kushoto kwenda kulia.

    Zoezi\(\PageIndex{76}\)

    Je, grafu ya mstari na mteremko\(m=\frac{1}{2}\) hutofautiana na grafu ya mstari na mteremko\(m=2 ?\)

    Zoezi\(\PageIndex{77}\)

    Kwa nini mteremko wa mstari wa wima “haijulikani”?

    Jibu

    Mstari wa wima una 0 kukimbia na tangu mgawanyiko na 0 haijulikani mteremko haujafafanuliwa.

    Self Check

    ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

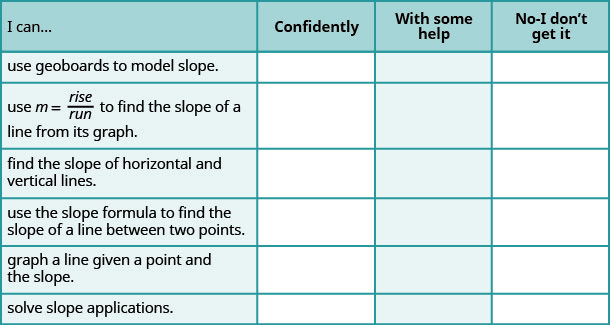
    Jedwali hili lina safu saba na nguzo nne. Mstari wa kwanza ni mstari wa kichwa na huandika kila safu. Safu ya kwanza inaitwa “Naweza...”, pili “Kwa uaminifu”, ya tatu “Kwa msaada fulani” na ya mwisho “Hapana - Siipati”. Katika safu ya “Naweza...” safu inayofuata inasoma “tumia geoboards kutengeneza mteremko.” Mstari wa tatu unasoma “tumia m sawa na kupanda kugawanywa na kukimbia ili kupata mteremko wa mstari kutoka kwenye grafu yake.” Mstari wa nne unasoma “tafuta mteremko wa mistari ya usawa na wima.” Mstari wa tano unasoma “tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya pointi mbili.” Mstari wa sita unasoma “grafu mstari uliopewa uhakika na mteremko.” Mstari wa mwisho unasoma “tatua programu za mteremko.” Nguzo zilizobaki ni tupu.

    ⓑ Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?

    faharasa

    geoboard
    Geoboard ni bodi yenye gridi ya magogo juu yake.
    mteremko hasi
    Mteremko mbaya wa mstari unashuka unaposoma kutoka kushoto kwenda kulia.
    mteremko mzuri
    Mteremko mzuri wa mstari unaendelea unaposoma kutoka kushoto kwenda kulia.
    kupanda
    Kuongezeka kwa mstari ni mabadiliko yake ya wima.
    kukimbia
    Kukimbia kwa mstari ni mabadiliko yake ya usawa.
    formula mteremko
    Mteremko wa mstari kati ya pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\) ni\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\).
    mteremko wa mstari
    Mteremko wa mstari ni\(m=\frac{\text { rise }}{\text { run }}\). Kuongezeka kwa hatua mabadiliko ya wima na kukimbia hatua za mabadiliko ya usawa.