Skip to main content
Global

4.4: Kuelewa Mteremko wa Line

  1. Last updated
  2. Save as PDF
  • Page ID
    177596

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Mwishoni mwa sehemu hii, utaweza:
    • Tumia geoboards kwa mfano mteremko
    • Tumia\(m = \frac{\text{rise}}{\text{run}}\) kupata mteremko wa mstari kutoka kwenye grafu yake
    • Pata mteremko wa mistari ya usawa na wima
    • Tumia formula ya mteremko ili kupata mteremko wa mstari kati ya pointi mbili
    • Grafu mstari uliotolewa na uhakika na mteremko
    • Kutatua maombi ya mteremko
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(\frac{1 - 4}{8 - 2}\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 1.6.31
    2. Gawanya:\(\frac{0}{4}, \frac{4}{0}\).
      Kama amekosa tatizo hili, kupitia Zoezi 1.10.16.
    3. Kurahisisha:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 1.6.4.

    Wakati graph equations linear, unaweza taarifa kwamba baadhi ya mistari tilt up kama wao kwenda kutoka kushoto kwenda kulia na baadhi ya mistari tilt chini. Baadhi ya mistari ni mwinuko sana na baadhi ya mistari ni flatter. Nini huamua kama line tilts juu au chini au kama ni mwinuko au gorofa?

    Katika hisabati, 'tilt' ya mstari inaitwa mteremko wa mstari. Dhana ya mteremko ina maombi mengi katika ulimwengu wa kweli. Upeo wa paa, daraja la barabara kuu, na barabara ya gurudumu ni mifano fulani ambapo unaona mteremko halisi. Na unapopanda baiskeli, unasikia mteremko unapopiga kupanda au pwani kuteremka.

    Katika sehemu hii, tutazingatia dhana ya mteremko.

    Tumia Geoboards kwa Mfano wa Mfano

    Geoboard ni bodi yenye gridi ya magogo juu yake. Kwa kutumia bendi mpira kwenye geoboard inatupa njia halisi ya mfano mistari kwenye gridi ya kuratibu. Kwa kunyoosha bendi ya mpira kati ya magogo mawili kwenye geoboard, tunaweza kugundua jinsi ya kupata mteremko wa mstari.

    Kufanya shughuli za Hisabati za Manipulative “Kuchunguza Slope” itakusaidia kuendeleza uelewa bora wa mteremko wa mstari. (Karatasi ya Grafu inaweza kutumika badala ya geoboard, ikiwa inahitajika.)

    Tutaanza kwa kunyoosha bendi ya mpira kati ya magogo mawili kama inavyoonekana kwenye Kielelezo\(\PageIndex{1}\).

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 4 na nguruwe katika safu ya 4, mstari wa 2, na kutengeneza mstari.
    Kielelezo\(\PageIndex{1}\)

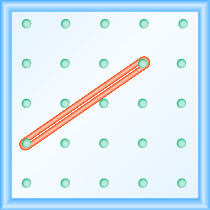
    Je, si ni kuangalia kama mstari?

    Sasa tunaweka sehemu moja ya bendi ya mpira moja kwa moja kutoka kwenye kigingi cha kushoto na karibu na kilele cha tatu ili kufanya pande za pembetatu sahihi, kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\)

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 2, kigingi katika safu ya 1, mstari wa 4, na kilele katika safu ya 4, mstari wa 2, na kutengeneza pembetatu sahihi. Kipande cha 1, 2 ni vertex ya angle ya shahada 90, wakati mstari kati ya 1, 4 na 4, mizigo 2 huunda hypotenuse ya pembetatu.
    Kielelezo\(\PageIndex{2}\)

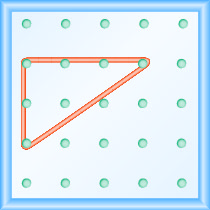
    Tunafanya kwa makini angle ya 90º karibu na kilele cha tatu, hivyo moja ya mistari iliyopangwa ni wima na nyingine ni ya usawa.

    Ili kupata mteremko wa mstari, tunapima umbali pamoja na pande za wima na za usawa za pembetatu. Umbali wa wima huitwa kupanda na umbali wa usawa unaitwa kukimbia, kama inavyoonekana kwenye Mchoro\(\PageIndex{3}\).

    Katika mfano huu, kuna mistari miwili ya perpendicular na mishale. Mstari wa kwanza unaendelea moja kwa moja hadi juu na inaitwa “kupanda”. Mshale wa pili unaendelea moja kwa moja upande wa kulia na umeandikwa “kukimbia”.
    Kielelezo\(\PageIndex{3}\)

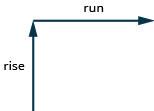
    Kama geoboard yetu na mpira bendi kuangalia kama moja inavyoonekana katika Kielelezo\(\PageIndex{4}\), kupanda ni 2. Bendi ya mpira inakwenda vitengo 2. (Kila nafasi ni kitengo kimoja.)

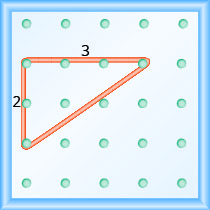
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 2, kigingi katika safu ya 1, mstari wa 4, na kigingi katika safu ya 4, mstari wa 2, kutengeneza pembetatu sahihi ambapo 1, 2 kigingi ni kipeo cha angle ya shahada 90 na mstari kati ya 1, 4 kigingi na 4, 2 kigingi huunda hypotenuse. mstari kati ya 1, 2 kigingi na 1, 4 kigingi kinachoitwa “2”. mstari kati ya 1, 2 kigingi na 4, 2 kigingi kinachoitwa “3”.
    Kielelezo\(\PageIndex{4}\)

    Kuongezeka kwa geoboard hii ni 2, kama bendi ya mpira inakwenda vitengo viwili.

    Kukimbia ni nini?

    Bendi ya mpira inakwenda vitengo 3. Kukimbia ni 3 (angalia Mchoro\(\PageIndex{4}\)).

    Mteremko wa mstari ni uwiano wa kupanda kwa kukimbia. Katika hisabati, daima hujulikana kwa barua m.

    MTEREMKO WA MSTARI

    Mteremko wa mstari wa mstari ni\(m = \frac{\text{rise}}{\text{run}}\).

    Kuongezeka kwa hatua mabadiliko ya wima na kukimbia hatua ya mabadiliko ya usawa kati ya pointi mbili kwenye mstari.

    Je, ni mteremko wa mstari kwenye geoboard katika Kielelezo\(\PageIndex{4}\)?

    \[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]

    Mstari una mteremko\(\frac{2}{3}\). Hii ina maana kwamba mstari unaongezeka vitengo 2 kwa kila vitengo 3 vya kukimbia.

    Tunapofanya kazi na geoboards, ni wazo nzuri ya kupata tabia ya kuanzia kwenye kigingi upande wa kushoto na kuunganisha kwenye kigingi upande wa kulia. Ikiwa kupanda kunakwenda juu ni chanya na ikiwa inakwenda chini ni hasi. Kukimbia utaenda kutoka kushoto kwenda kulia na kuwa chanya.

    Zoezi\(\PageIndex{1}\)

    Je! Mteremko wa mstari kwenye geoboard umeonyeshwa nini?

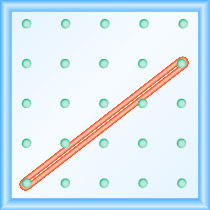
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 5 na nguruwe katika safu ya 5, mstari wa 2, na kutengeneza mstari.

    Jibu

    Tumia ufafanuzi wa mteremko:\(m = \frac{\text{rise}}{\text{run}}\).

    Anza kwenye kigingi cha kushoto na uhesabu nafasi hadi kulia kufikia kilele cha pili.

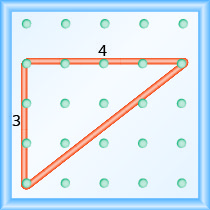
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 2, kigingi katika safu ya 1, mstari wa 5 na kigingi katika safu ya 5, mstari wa 2, na kutengeneza pembetatu sahihi. Kipande cha 1, 2 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwenye kigingi cha 1, 5 hadi kilele cha 5, 2 huunda hypotenuse ya pembetatu. Mstari kutoka kwenye kigingi cha 1, 2 hadi kilele cha 1, 5 kinaitwa “3”. Mstari kutoka kwa kigingi cha 1, 2 hadi kilele cha 5, 2 kinachoitwa “4”.

    \[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]

    Hii ina maana kwamba mstari unaongezeka vitengo 3 kwa kila vitengo 4 vya kukimbia.

    Zoezi\(\PageIndex{2}\)

    Je! Mteremko wa mstari kwenye geoboard umeonyeshwa nini?

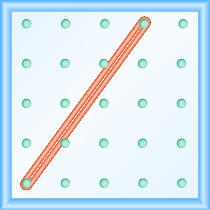
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 5 na nguruwe katika safu ya 4, mstari wa 1, kutengeneza mstari.

    Jibu

    \(\frac{4}{3}\)

    Zoezi\(\PageIndex{3}\)

    Je! Mteremko wa mstari kwenye geoboard umeonyeshwa nini?

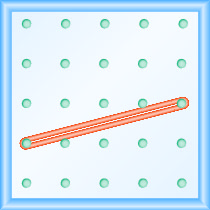
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 4 na nguruwe katika safu ya 5, mstari wa 3, na kutengeneza mstari.

    Jibu

    \(\frac{1}{4}\)

    Zoezi\(\PageIndex{4}\)

    Je! Mteremko wa mstari kwenye geoboard umeonyeshwa nini?

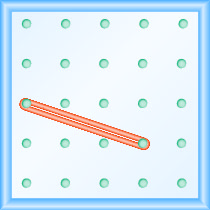
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 3 na nguruwe katika safu ya 4, mstari wa 4, na kutengeneza mstari.

    Jibu

    Tumia ufafanuzi wa mteremko:\(m = \frac{\text{rise}}{\text{run}}\).

    Anza kwenye kigingi cha kushoto na uhesabu vitengo chini na kulia kufikia kigingi cha pili.

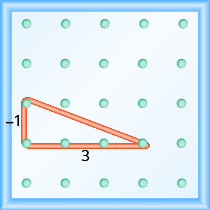
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 3, kigingi katika safu ya 1, mstari wa 4 na kigingi katika safu ya 4, mstari wa 4, na kutengeneza pembetatu sahihi. Kipande cha 1, 3 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwa kigingi cha 1, 4 hadi kilele cha 4, 4 huunda hypotenuse ya pembetatu. Mstari kutoka kwa kigingi cha 1, 3 hadi kilele cha 1, 4 kinachoitwa “hasi 1". Mstari kutoka kwenye kigingi cha 1, 4 hadi kilele cha 4, 4 kinaitwa “3”.

    \[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]

    Hii ina maana kwamba mstari hupungua kitengo 1 kwa kila vitengo 3 vya kukimbia.

    Zoezi\(\PageIndex{5}\)

    Je, ni mteremko wa mstari kwenye geoboard?

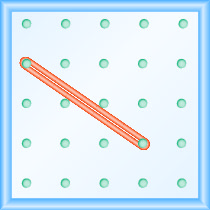
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 2 na nguruwe katika safu ya 4, mstari wa 4, na kutengeneza mstari.

    Jibu

    \(-\frac{2}{3}\)

    Zoezi\(\PageIndex{6}\)

    Je, ni mteremko wa mstari kwenye geoboard?

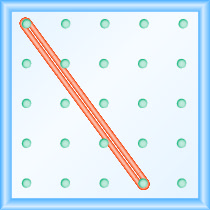
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 1 na nguruwe katika safu ya 4, mstari wa 5, na kutengeneza mstari.

    Jibu

    \(-\frac{4}{3}\)

    Kumbuka kwamba katika Zoezi\(\PageIndex{1}\) mteremko ni chanya na katika Zoezi\(\PageIndex{4}\) mteremko ni hasi. Je! Unaona tofauti yoyote katika mistari miwili iliyoonyeshwa kwenye Kielelezo (a) na Kielelezo (b)?

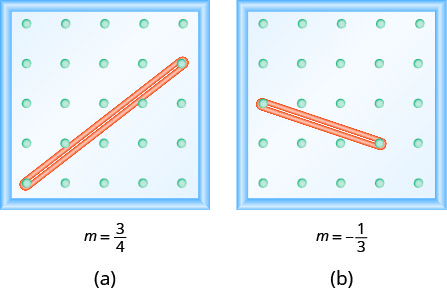
    Takwimu inaonyesha gridi mbili za magogo yaliyowekwa sawa, moja iliyoandikwa (a) na moja iliyoandikwa (b). Kuna nguzo 5 na safu 5 za magogo katika kila gridi ya taifa. Katika gridi ya taifa (a), bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 5 na kigingi katika safu ya 5, mstari wa 2, na kutengeneza mstari. Chini ya gridi hii ni mteremko wa mstari unaofafanuliwa kama m sawa na 3 nne. Katika gridi ya taifa (b), bendi ya mpira imetambulishwa kati ya nguruwe katika safu ya 1, mstari wa 3 na kigingi katika safu ya 4, mstari wa 4, na kutengeneza mstari. Chini ya gridi hii ni mteremko wa mstari unaofafanuliwa kama m sawa na hasi 1 tatu.
    Kielelezo\(\PageIndex{5}\)

    Tunasoma 'mstari kutoka kushoto kwenda kulia kama tunavyosoma maneno kwa Kiingereza. Unaposoma kutoka kushoto kwenda kulia, mstari katika Kielelezo (a) unakwenda; ina mteremko mzuri. Mstari katika Kielelezo (b) unashuka; ina mteremko hasi.

    MTEREMKO MZURI NA HASI
    Takwimu inaonyesha mistari miwili upande kwa upande. Mstari upande wa kushoto ni mstari wa diagonal unaoongezeka kutoka kushoto kwenda kulia. Inaitwa “Mteremko mzuri”. Mstari wa kulia ni mstari wa diagonal ambao hupungua kutoka kushoto kwenda kulia. Inaandikwa “Mteremko mbaya”.
    Kielelezo\(\PageIndex{6}\)
    Zoezi\(\PageIndex{7}\)

    Tumia geoboard ili kuiga mstari na mteremko\(\frac{1}{2}\).

    Jibu

    Ili kutengeneza mstari kwenye geoboard, tunahitaji kupanda na kukimbia.

    \(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)

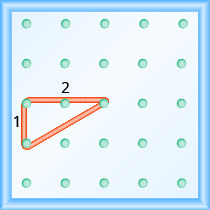
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 3, kigingi katika safu ya 1, mstari wa 4 na kigingi katika safu ya 3, mstari wa 3, na kutengeneza pembetatu sahihi. Kipande cha 1, 3 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwenye kigingi cha 1, 4 hadi kilele cha 3, 3 huunda hypotenuse ya pembetatu. Mstari kutoka kwenye kigingi cha 1, 3 hadi kilele cha 1, 4 kinaitwa “1”. Mstari kutoka kwa kigingi cha 1, 3 hadi kilele cha 3, 3 kinaitwa “2”.

    Hypotenuse ya pembetatu sahihi iliyoundwa na bendi ya mpira inawakilisha mstari ambao mteremko ni\(\frac{1}{2}\).

    Zoezi\(\PageIndex{8}\)

    Mfano mteremko\(m = \frac{1}{3}\). Chora picha ili kuonyesha matokeo yako.

    Jibu

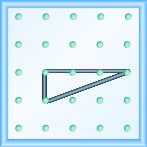
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 2, mstari wa 3, kigingi katika safu ya 2, mstari wa 4 na kigingi katika safu ya 5, mstari wa 3, na kutengeneza pembetatu sahihi. Kipande cha 2, 3 kinaunda vertex ya angle ya shahada ya 90 na mstari kutoka kwenye kilele cha 2, 4 hadi kilele cha 5, 3 huunda hypotenuse ya pembetatu.

    Zoezi\(\PageIndex{9}\)

    Mfano mteremko\(m = \frac{3}{2}\). Chora picha ili kuonyesha matokeo yako.

    Jibu

    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 1, kigingi katika safu ya 1, mstari wa 4 na kigingi katika safu ya 3, mstari wa 1, na kutengeneza pembetatu sahihi. Kipande cha 1, 1 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwenye kigingi cha 1, 4 hadi kilele cha 3, 1 huunda hypotenuse ya pembetatu.

    Zoezi\(\PageIndex{10}\)

    Tumia geoboard ili kuiga mstari na mteremko\(\frac{-1}{4}\).

    Jibu

    \(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)

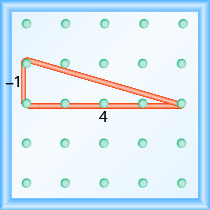
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 2, kigingi katika safu ya 1, mstari wa 3 na kigingi katika safu ya 5, mstari wa 3, na kutengeneza pembetatu sahihi. Kipande cha 1, 3 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwenye kigingi cha 1, 2 hadi kilele cha 5, 3 huunda hypotenuse ya pembetatu. Mstari kutoka kwa kigingi cha 1, 2 hadi kilele cha 1, 3 kinaitwa “hasi 1". Mstari kutoka kwenye kigingi cha 1, 3 hadi kilele cha 5, 3 kinaitwa “4”.

    Hypotenuse ya pembetatu sahihi iliyoundwa na bendi ya mpira inawakilisha mstari ambao mteremko ni\(\frac{-1}{4}\).

    Zoezi\(\PageIndex{11}\)

    Mfano mteremko\(m = \frac{-2}{3}\). Chora picha ili kuonyesha matokeo yako.

    Jibu

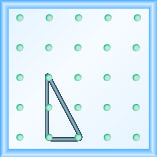
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 2, mstari wa 3, kigingi katika safu ya 2, mstari wa 5 na kilele katika safu ya 3, mstari wa 5, na kutengeneza pembetatu sahihi. Kipande cha 2, 5 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwenye kilele cha 2, 3 hadi kilele cha 3, 5 huunda hypotenuse ya pembetatu.

    Zoezi\(\PageIndex{12}\)

    Mfano mteremko\(m = \frac{-1}{3}\). Chora picha ili kuonyesha matokeo yako.

    Jibu

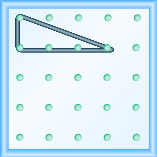
    Takwimu inaonyesha gridi ya magogo yaliyowekwa sawa. Kuna nguzo 5 na safu 5 za magogo. Bendi ya mpira imetambulishwa kati ya kigingi katika safu ya 1, mstari wa 1, kigingi katika safu ya 1, mstari wa 2 na kigingi katika safu ya 4, mstari wa 2, na kutengeneza pembetatu sahihi. Kipande cha 1, 2 kinaunda vertex ya angle ya shahada 90 na mstari kutoka kwa kigingi cha 1, 1 hadi 4, 2 kigingi huunda hypotenuse ya pembetatu.

    Tumia\(m = \frac{\text{rise}}{\text{run}}\) Kupata Slope ya Line kutoka Grafu yake

    Sasa, tutaangalia baadhi ya grafu kwenye ndege ya kuratibu xy-na kuona jinsi ya kupata mteremko wao. Njia hiyo itakuwa sawa na kile tulichotaja tu kwenye geoboards zetu.

    Ili kupata mteremko, tunapaswa kuhesabu kupanda na kukimbia. Lakini tunaanza wapi?

    Tunapata pointi mbili kwenye mstari ambao kuratibu ni integers. Sisi kisha kuanza na uhakika upande wa kushoto na mchoro pembetatu sahihi, ili tuweze kuhesabu kupanda na kukimbia.

    Zoezi\(\PageIndex{13}\):

    Pata mteremko wa mstari ulioonyeshwa.

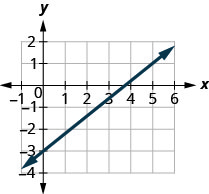
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 6 na y-axis huendesha kutoka hasi 4 hadi 2. Mstari unapita kupitia pointi (0, hasi 3) na (5, 1).

    Jibu

    Jedwali hili lina nguzo tatu na safu nne. Mstari wa kwanza unasema, “Hatua ya 1. Pata pointi mbili kwenye grafu ambazo kuratibu ni integers. Mark (0, hasi 3) na (5, 1).” Kwa upande wa kulia ni mstari uliowekwa kwenye ndege ya kuratibu ya x y. Mhimili wa x-wa ndege huendesha kutoka hasi 1 hadi 6. Mhimili wa y wa ndege unatoka hasi 4 hadi 2. Vipengele (0, hasi 3) na (5, 1) vinapangwa.Mstari wa pili unasema, “Hatua ya 2. Kuanzia na hatua upande wa kushoto, mchoro pembetatu sahihi, kutoka hatua ya kwanza hadi hatua ya pili. Kuanzia saa (0, hasi 3), mchoro pembetatu sahihi kwa (5, 1).” Katika grafu upande wa kulia, hatua ya ziada imepangwa (0, 1). Vipengele vitatu vinaunda pembetatu sahihi, na mstari kutoka (0, hasi 3) hadi (5, 1) kutengeneza hypotenuse na mistari kutoka (0, hasi 3) hadi (0, 1) na (0, 1) hadi (5, 1) kutengeneza miguu.Mstari wa tatu kisha unasema, “Hatua ya 3. Hesabu kupanda na kukimbia kwenye miguu ya pembetatu.” Kuongezeka ni 4 na kukimbia ni 5.Mstari wa nne unasema, “Hatua ya 4. Chukua uwiano wa kupanda ili kukimbia ili kupata mteremko. Tumia formula ya mteremko. Badilisha maadili ya kupanda na kukimbia.” Kwa haki ni formula ya mteremko, m sawa na kupanda kugawanywa na kukimbia. Mteremko wa mstari ni 4 umegawanyika na 5, au nne tano. Hii ina maana kwamba y kuongezeka 4 vitengo kama x ongezeko 5 vitengo.

    Zoezi\(\PageIndex{14}\)

    Pata mteremko wa mstari ulioonyeshwa.

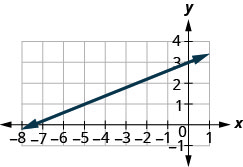
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 8 hadi 1 na y-axis huendesha kutoka hasi 1 hadi 4. Mstari unapita kupitia pointi (hasi 5, 1) na (0, 3).

    Jibu

    \(\frac{2}{5}\)

    Zoezi\(\PageIndex{15}\)

    Pata mteremko wa mstari ulioonyeshwa.

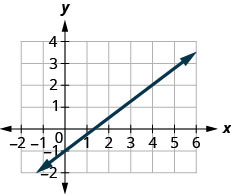
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 5 na y-axis huendesha kutoka hasi 2 hadi 4. Mstari unapita kupitia pointi (0, hasi 1) na (4, 2).

    Jibu

    \(\frac{3}{4}\)

    PATA MTEREMKO WA MSTARI KUTOKA KWENYE GRAFU YAKE
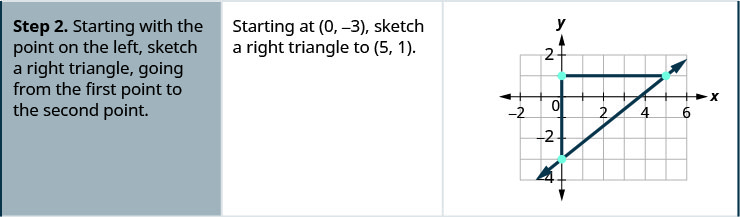
    1. Pata pointi mbili kwenye mstari ambao kuratibu ni integers.
    2. Kuanzia na hatua upande wa kushoto, mchoro pembetatu sahihi, kutoka hatua ya kwanza hadi hatua ya pili.
    3. Kuhesabu kupanda na kukimbia kwenye miguu ya pembetatu.
    4. Chukua uwiano wa kupanda ili kukimbia ili kupata mteremko,\(m = \frac{\text{rise}}{\text{run}}\).
    Zoezi\(\PageIndex{16}\)

    Pata mteremko wa mstari ulioonyeshwa.

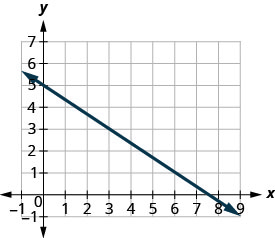
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 9 na y-axis huendesha kutoka hasi 1 hadi 7. Mstari unapita kupitia pointi (0, 5), (3, 3), na (6, 1).

    Jibu
    Pata pointi mbili kwenye grafu ambazo kuratibu ni integers. (0,5) na (3,3)
    Ni hatua gani iliyo upande wa kushoto? (0,5)
    Kuanzia saa (0,5), mchoro pembetatu sahihi kwa (3,3). .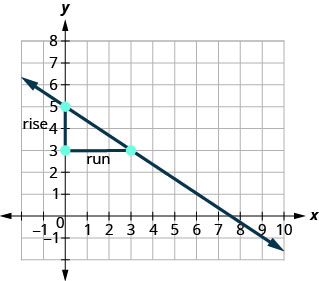
    Hesabu kupanda - ni hasi. Kuongezeka ni -2.
    Hesabu kukimbia. Kukimbia ni 3.
    Tumia formula ya mteremko. \(m = \frac{\text{rise}}{\text{run}}\)
    Badilisha maadili ya kupanda na kukimbia. \(m = \frac{-2}{3}\)
    Kurahisisha. \(m = -\frac{2}{3}\)
      Mteremko wa mstari ni\(-\frac{2}{3}\).

    Hivyo y huongezeka kwa vitengo 3 kama xx inapungua kwa vitengo 2.

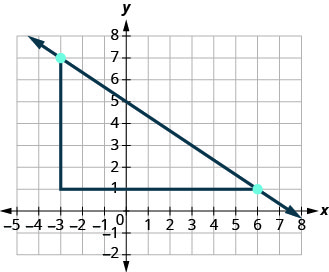
    Nini ikiwa tulitumia pointi (-3,7) na (6,1) ili kupata mteremko wa mstari?

    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 3, 7) na (6, 1). Hatua ya ziada imepangwa (hasi 3, 1). Vipengele vitatu vinaunda pembetatu sahihi, na mstari kutoka (hasi 3, 7) hadi (6, 1) kutengeneza hypotenuse na mistari kutoka (hasi 3, 7) hadi hasi 1, 7) na kutoka (hasi 1, 7) hadi (6, 1) kutengeneza miguu.

    Kuongezeka itakuwa -6 na kukimbia itakuwa 9. Kisha\(m = \frac{-6}{9}\), na kwamba simplifies kwa\(m = -\frac{2}{3}\). Kumbuka, haijalishi ni pointi gani unazotumia-mteremko wa mstari daima ni sawa.

    Zoezi\(\PageIndex{17}\)

    Pata mteremko wa mstari ulioonyeshwa.

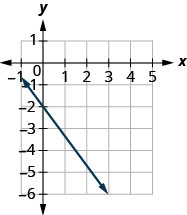
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 5 na y-axis huendesha kutoka hasi 6 hadi 1. Mstari unapita kupitia pointi (0, hasi 2) na (3, hasi 6).

    Jibu

    \(-\frac{4}{3}\)

    Zoezi\(\PageIndex{18}\)

    Pata mteremko wa mstari ulioonyeshwa.

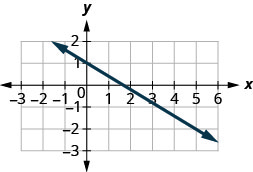
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 3 hadi 6 na y-axis huendesha kutoka hasi 3 hadi 2. Mstari unapita kupitia pointi (0, 1) na (5, hasi 2).

    Jibu

    \(-\frac{3}{5}\)

    Katika mifano miwili iliyopita, mistari ilikuwa y -intercepts na maadili integer, hivyo ilikuwa rahisi kutumia y -intercept kama moja ya pointi ili kupata mteremko. Katika mfano unaofuata, y -intercept ni sehemu. Badala ya kutumia hatua hiyo, tutaweza kuangalia kwa pointi nyingine mbili ambao kuratibu ni integers. Hii itafanya mahesabu ya mteremko iwe rahisi.

    Zoezi\(\PageIndex{19}\)

    Pata mteremko wa mstari ulioonyeshwa.

    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka 0 hadi 8 na mhimili wa y huendesha kutoka 0 hadi 7. Mstari unapita kupitia pointi (2, 3) na (7, 6).

    Jibu
    Pata pointi mbili kwenye grafu ambazo kuratibu ni integers. (2,3) na (7,6)
    Ni hatua gani iliyo upande wa kushoto? (2,3)
    Kuanzia saa (2,3), mchoro pembetatu sahihi kwa (7,6). .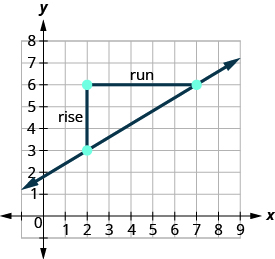
    Hesabu kupanda. Kuongezeka ni 3.
    Hesabu kukimbia. Kukimbia ni 5.
    Tumia formula ya mteremko. \(m = \frac{\text{rise}}{\text{run}}\)
    Badilisha maadili ya kupanda na kukimbia. \(m = \frac{3}{5}\)
      Mteremko wa mstari ni\(\frac{3}{5}\).

    Hii ina maana kwamba y kuongezeka 5 vitengo kama x ongezeko 3 vitengo.

    Tulipotumia geoboards kuanzisha dhana ya mteremko, tulisema kwamba tutakuwa daima kuanza na hatua upande wa kushoto na kuhesabu kupanda na kukimbia kufikia hatua ya kulia. Kwa njia hiyo kukimbia mara zote ilikuwa chanya na kupanda kuamua kama mteremko ulikuwa chanya au hasi.

    Nini kitatokea kama sisi ilianza na uhakika juu ya haki?

    Hebu kutumia pointi (2,3) na (7,6) tena, lakini sasa tutaanza saa (7,6).

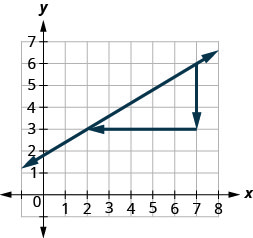
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x huendesha kutoka 0 hadi 8. Y -axis inaendesha kutoka 0 hadi 7. Mstari unapita kupitia pointi (2, 3) na (7, 6). Hatua ya ziada imepangwa (7, 3). Vipengele vitatu vinaunda pembetatu sahihi, na mstari kutoka (2, 3) hadi (7, 6) kutengeneza hypotenuse na mistari kutoka (2, 3) hadi (7, 3) na kutoka (7, 3) hadi (7, 6) kutengeneza miguu.
    \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
    Haijalishi wapi kuanza-mteremko wa mstari daima ni sawa.
    Zoezi\(\PageIndex{20}\)

    Pata mteremko wa mstari ulioonyeshwa.

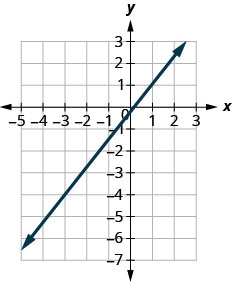
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 4 hadi 2 na y-axis huendesha kutoka hasi 6 hadi 2. Mstari unapita kupitia pointi (hasi 3, 4) na (1, 1).

    Jibu

    \(\frac{5}{4}\)

    Zoezi\(\PageIndex{21}\)

    Pata mteremko wa mstari ulioonyeshwa.

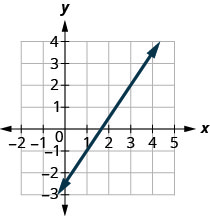
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 4 na y-axis huendesha kutoka hasi 2 hadi 3. Mstari unapita kupitia pointi (1, hasi 1) na (3, 2).

    Jibu

    \(\frac{3}{2}\)

    Pata mteremko wa Mistari ya Ulalo na Wima

    Je! Unakumbuka kile kilichokuwa maalum kuhusu mistari ya usawa na wima? Equations yao ilikuwa na variable moja tu.

    \[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]

    Hivyo tunawezaje kupata mteremko wa mstari wa usawa y=4y=4? Njia moja itakuwa grafu mstari usawa, kupata pointi mbili juu yake, na kuhesabu kupanda na kukimbia. Hebu tuone kinachotokea tunapofanya hivyo.

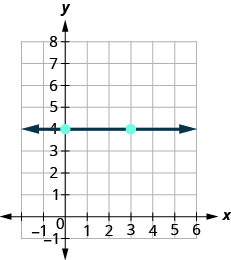
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 5 na y-axis huendesha kutoka hasi 1 hadi 7. Mstari unapita kupitia pointi (0, 4) na (3, 4).
    Kielelezo\(\PageIndex{7}\)

    \(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)

    Mistari yote ya usawa ina mteremko 0. Wakati y -kuratibu ni sawa, kupanda ni 0.

    MTEREMKO WA MSTARI USAWA

    Mteremko wa mstari usio na usawa, y=b, ni 0.

    Ghorofa ya chumba chako ni usawa. Mteremko wake ni 0. Ikiwa umeweka mpira kwenye sakafu kwa uangalifu, hautaondoka.

    Sasa, tutazingatia mstari wa wima, mstari.

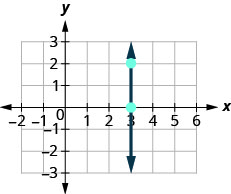
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 1 hadi 5 na y-axis huendesha kutoka hasi 2 hadi 2. Mstari unapita kupitia pointi (3, 0) na (3, 2).
    Kielelezo\(\PageIndex{8}\)

    \(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)

    Lakini hatuwezi kugawa na 0. Idara na 0 si defined. Kwa hiyo tunasema kwamba mteremko wa mstari wa wima x=3x=3 haijulikani.

    Mteremko wa mstari wowote wa wima haujafafanuliwa. Wakati x -kuratibu ya mstari ni sawa, kukimbia ni 0.

    MTEREMKO WA MSTARI WA WIMA

    Mteremko wa mstari wa wima, x=a, haijulikani.

    Zoezi\(\PageIndex{22}\)

    Pata mteremko wa kila mstari:

    ⓐ x=8 ⓑ y=-5.

    Jibu

    ⓐ x=8
    Hii ni mstari wa wima.
    Mteremko wake haujafafanuliwa.

    ⓑ y=-5
    Hii ni mstari usio na usawa.
    Ina mteremko 0.

    Zoezi\(\PageIndex{23}\)

    Pata mteremko wa mstari: x=4-7.

    Jibu

    haijafafanuliwa

    Zoezi\(\PageIndex{24}\)

    Pata mteremko wa mstari: y=7.

    Jibu

    0

    MWONGOZO HARAKA KWENYE MTEREMKO WA MISTARI
    Takwimu hii inaonyesha mistari minne na mishale. Mstari wa kwanza unatoka na kukimbia kwa haki. Ina mteremko mzuri. Mstari wa pili unaanguka chini na huendesha kwa haki. Ina mteremko hasi. Mstari wa tatu hauinuka wala huanguka, kupanua kwa usawa katika mwelekeo wowote. Ina mteremko wa sifuri. Mstari wa nne ni wima kabisa, mwisho mmoja unainuka na mwingine huinuka chini, bila kukimbia kwa kushoto wala kulia. Ina mteremko usiojulikana.
    Kielelezo\(\PageIndex{9}\)

    Kumbuka, 'tunasoma' mstari kutoka kushoto kwenda kulia, kama tunavyosoma maneno yaliyoandikwa kwa Kiingereza.

    Tumia Mfumo wa Slope ili kupata Slope ya Mstari Kati ya Pointi mbili

    Kufanya shughuli za Hisabati za Manipulative “Slope of Lines Kati ya Points mbili” itakusaidia kuendeleza uelewa bora wa jinsi ya kupata mteremko wa mstari kati ya pointi mbili.

    Wakati mwingine tutaweza haja ya kupata mteremko wa mstari kati ya pointi mbili wakati hatuna grafu kuhesabu nje kupanda na kukimbia. Tunaweza kupanga pointi kwenye karatasi ya gridi ya taifa, kisha kuhesabu kupanda na kukimbia, lakini kama tutakavyoona, kuna njia ya kupata mteremko bila kuchora. Kabla ya kupata hiyo, tunahitaji kuanzisha baadhi ya notation algebraic.

    Tumeona kwamba jozi kuamuru (x, y) anatoa kuratibu ya uhakika. Lakini tunapofanya kazi na mteremko, tunatumia pointi mbili. Je! Ishara hiyo (x, y) inaweza kutumiwa kuwakilisha pointi mbili tofauti? Wataalamu wa hisabati hutumia michango ili kutofautisha pointi.

    \[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]

    Matumizi ya michango katika hesabu ni sawa na matumizi ya jina la mwisho initials katika shule ya msingi. Labda unakumbuka Laura C. na Laura M. katika darasa lako la daraja la tatu?

    Tutatumia\(\left(x_{1}, y_{1}\right)\) kutambua hatua ya kwanza na\(\left(x_{2}, y_{2}\right)\) kutambua hatua ya pili.

    Kama tulikuwa na pointi zaidi ya mbili, tunaweza kutumia\(\left(x_{3}, y_{3}\right)\),\(\left(x_{4}, y_{4}\right)\), na kadhalika.

    Hebu tuone jinsi kupanda na kukimbia kuhusiana na kuratibu za pointi mbili kwa kuchunguza mwingine mteremko wa mstari kati ya pointi (2,3) na (7,6).

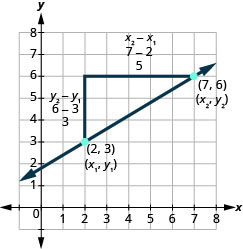
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka 0 hadi 7. Mstari unapita kupitia pointi (2, 3) na (7, 6), ambazo zimepangwa na zimeandikwa. Jozi iliyoamriwa (2, 3) imeandikwa (x subscript 1, y subscript 1). Jozi iliyoamriwa (7, 6) imeandikwa (x subscript 2, y subscript 2). Hatua ya ziada imepangwa (2, 6). Vipengele vitatu vinaunda pembetatu sahihi, na mstari kutoka (2, 3) hadi (7, 6) kutengeneza hypotenuse na mistari kutoka (2, 3) hadi (2, 6) na kutoka (2, 6) hadi (7, 6) kutengeneza miguu. Mguu wa kwanza, kutoka (2, 3) hadi (2, 6) umeandikwa y subscript 2 minus y subscript 1, 6 minus 3, na 3. Mguu wa pili, kutoka (2, 3) hadi (7, 6), umeandikwa x subscript 2 minus x subscript 1, y minus 2, na 5.
    Kielelezo\(\PageIndex{10}\)

    Kwa kuwa tuna pointi mbili, tutatumia nukuu ya usajili,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\).

    Kwenye grafu, tulihesabu kupanda kwa 3 na kukimbia kwa 5.

    Angalia kwamba kupanda kwa 3 kunaweza kupatikana kwa kuondoa y -kuratibu 6 na 3.

    \[3=6-3\]

    Na kukimbia kwa 5 kunaweza kupatikana kwa kuondoa x -kuratibu 7 na 2.

    \[5 = 7 - 2\]

    Tunajua\(m = \frac{\text{rise}}{\text{run}}\). Hivyo\(m = \frac{3}{5}\).

    Tunaandika tena kupanda na kukimbia kwa kuweka katika kuratibu\(m = \frac{6-3}{7-2}\)

    Lakini 6 ni y2, y -kuratibu ya hatua ya pili na 3 ni y1, y -kuratibu ya hatua ya kwanza.

    Hivyo tunaweza kuandika upya mteremko kwa kutumia nukuu subscript. \(m = \frac{y2-y1}{7-2}\)

    Pia, 7 ni x2, x -kuratibu ya hatua ya pili na 2 ni x1, x -kuratibu ya hatua ya kwanza.

    Kwa hiyo, tena, tunaandika upya mteremko kwa kutumia nukuu ya usajili. \(m = \frac{y2-y1}{x2-x1}\)

    Tumeonyesha kwamba\(m = \frac{y2-y1}{x2-x1}\) ni kweli toleo jingine la\(m = \frac{\text{rise}}{\text{run}}\). Tunaweza kutumia formula hii ili kupata mteremko wa mstari wakati tuna pointi mbili kwenye mstari.

    MFUMO WA MTEREMKO

    Mteremko wa mstari kati ya pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\) ni

    \[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]

    Hii ni formula ya mteremko.

    Mteremko ni:

    \[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]

    Zoezi\(\PageIndex{25}\)

    Tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya pointi (1,2) na (4,5).

    Jibu

    \(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)

    Hebu tuhakikishe hili kwa kuhesabu mteremko kwenye grafu kutumia\(m = \frac{\text{rise}}{\text{run}}\).

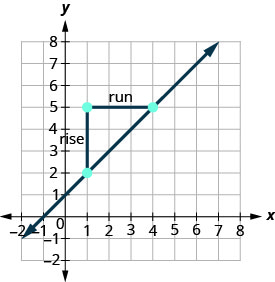
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes ya ndege huendesha kutoka 0 hadi 7. Mstari unapita kupitia pointi (1, 2) na (4, 5), ambazo zimepangwa. Hatua ya ziada imepangwa (1, 5). Vipengele vitatu vinaunda pembetatu sahihi, na mstari kutoka (1, 2) hadi (4, 5) kutengeneza hypotenuse na mistari kutoka (1, 2) hadi (1, 5) na kutoka (1, 5) hadi (4, 5) kutengeneza miguu. Mguu kutoka (1, 2) hadi (1, 5) umeandikwa “kupanda” na mguu kutoka (1, 5) hadi (4, 5) umeandikwa “kukimbia”.

    Haijalishi ni hatua gani unayoita hatua #1 na ni nani unayoita uhakika #2. Mteremko utakuwa sawa. Jaribu hesabu mwenyewe.

    Zoezi\(\PageIndex{26}\)

    Tumia fomu ya mteremko ili kupata mteremko wa mstari kupitia pointi: (8,5) na (6,3).

    Jibu

    1

    Zoezi\(\PageIndex{27}\)

    Tumia fomu ya mteremko ili kupata mteremko wa mstari kupitia pointi: (1,5) na (5,9).

    Jibu

    1

    Zoezi\(\PageIndex{28}\)

    Tumia formula ya mteremko ili kupata mteremko wa mstari kupitia pointi (-2, 1-3) na (-7,4).

    Jibu

    \(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)

    Hebu tuhakikishe mteremko huu kwenye grafu iliyoonyeshwa.

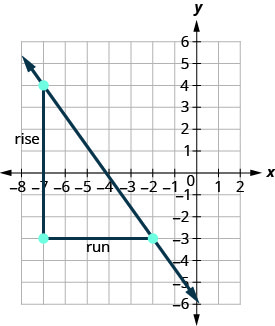
    Grafu inaonyesha ndege ya kuratibu x y. Mhimili wa x-wa ndege unatoka hasi 8 hadi 2 na y axis wa ndege huendesha kutoka hasi 6 hadi 5. Mstari unapita kupitia pointi (hasi 7, 4) na (hasi 2, hasi 3), ambazo zimepangwa na zimeandikwa. Hatua ya ziada imepangwa (hasi 7, hasi 3). pointi tatu kuunda pembetatu haki, na mstari kutoka (hasi 7, 4) kwa (hasi 2, hasi 3) kutengeneza hypotenuse na mistari kutoka (hasi 7, 4) kwa (hasi 7, hasi 3) na kutoka (hasi 7, hasi 3) kwa (hasi 2, hasi 3) kutengeneza miguu. Mguu kutoka (hasi 7, 4) hadi (hasi 7, hasi 3) inaitwa “kupanda” na mguu kutoka (hasi 7, hasi 3) hadi (hasi 2, hasi 3) inaitwa “kukimbia”.

    \[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]

    Zoezi\(\PageIndex{29}\)

    Tumia fomu ya mteremko ili kupata mteremko wa mstari kupitia pointi: (-3,4) na (2, -1).

    Jibu

    -1

    Zoezi\(\PageIndex{30}\)

    Tumia fomu ya mteremko ili kupata mteremko wa mstari kupitia jozi la pointi: (-2,6) na (-3, -4).

    Jibu

    10

    Grafu Mstari Kutolewa Point na Slope

    Hadi sasa, katika sura hii, tuna graphed mistari kwa pointi njama, kwa kutumia intercepts, na kwa kutambua mistari usawa na wima.

    Njia nyingine moja tunaweza kutumia kwa mistari ya grafu inaitwa njia ya uhakika-mteremko. Tutatumia njia hii tunapojua hatua moja na mteremko wa mstari. Tutaanza kwa kupanga njama na kisha kutumia ufafanuzi wa mteremko kuteka grafu ya mstari.

    Zoezi\(\PageIndex{31}\)

    Grafu mstari unaopita kupitia hatua (1, -1) ambao mteremko wake ni\(m = \frac{3}{4}\).

    Jibu

    Jedwali hili lina nguzo tatu na safu nne. Mstari wa kwanza unasema, “Hatua ya 1. Panda hatua iliyotolewa. Plot (1, hasi 1).” Kwa haki ni grafu ya ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 1 hadi 7. Mhimili wa y wa ndege unatoka hasi 3 hadi 4. Hatua (0, hasi 1) imepangwa.Mstari wa pili unasema, “Hatua ya 2. Kutumia formula mteremko m sawa kupanda kugawanywa na kukimbia kutambua kupanda na kukimbia.” Kuongezeka na kukimbia ni 3 na 4, hivyo m sawa na 3 imegawanywa na 4.Mstari wa tatu unasema “Hatua ya 3. Kuanzia kwenye hatua iliyotolewa, uhesabu kupanda na kukimbia ili alama ya pili.” Tunaanza saa (1, hasi 1) na kuhesabu kupanda na kukimbia. Up vitengo tatu na haki 4 vitengo. Katika grafu upande wa kulia, pointi mbili za ziada zimepangwa: (1, 2), ambayo ni vitengo 3 kutoka (1, hasi 1), na (5, 2), ambayo ni vitengo 3 hadi na vitengo 4 kutoka (1, hasi 1).Mstari wa nne unasema “Hatua ya 4. Unganisha pointi kwa mstari.” Kwenye grafu upande wa kulia, mstari hutolewa kupitia pointi (1, hasi 1) na (5, 2). Mstari huu pia ni hypotenuse ya pembetatu sahihi inayoundwa na pointi tatu, (1, hasi 1), (1, 2) na (5, 2).

    Zoezi\(\PageIndex{32}\)

    Grafu mstari unaopita kupitia hatua (2, -1) na mteremko\(m = \frac{4}{3}\).

    Jibu

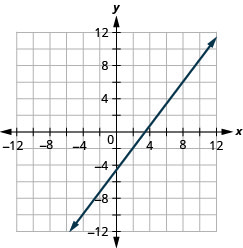
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (hasi 4, hasi 10) na (2, hasi 2).

    Zoezi\(\PageIndex{33}\)

    Grafu mstari unaopita kupitia hatua (-2,3) na mteremko\(m=\frac{1}{4}\).

    Jibu

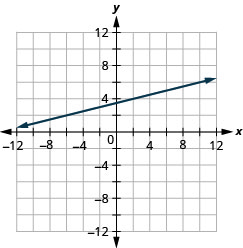
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unapita kupitia pointi (hasi 2, 3) na (10, 6).

    GRAFU MSTARI ULIOPEWA HATUA NA MTEREMKO.
    1. Panda hatua iliyotolewa.
    2. Tumia formula\(m=\frac{\text { rise }}{\text { rise }}\) ya mteremko kutambua kupanda na kukimbia.
    3. Kuanzia kwenye hatua iliyotolewa, uhesabu kupanda na kukimbia ili alama ya pili.
    4. Unganisha pointi kwa mstari.
    Zoezi\(\PageIndex{34}\)

    Grafu mstari na y -intercept 2 ambao mteremko wake ni\(m=−\frac{2}{3}\).

    Jibu

    Panda hatua iliyotolewa, y -intercept, (0,2).

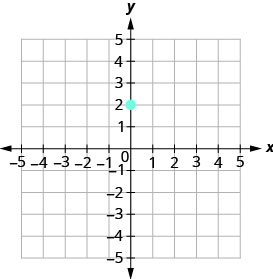
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Hatua (0, 2) imepangwa.

    \(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)

    Hesabu kupanda na kukimbia. Andika alama ya pili.

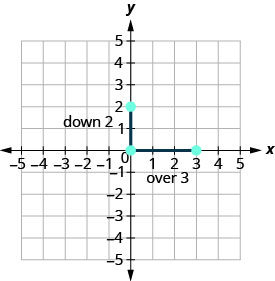
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Pointi (0, 2), (0, 0), na (3,0) zimepangwa na zimeandikwa. Mstari kutoka (0, 2) hadi (0, 0) umeandikwa “chini 2" na mstari kutoka (0, 0) hadi (3, 0) umeandikwa “haki 3".

    Unganisha pointi mbili na mstari.

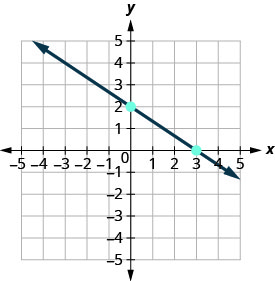
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Mstari unapita kupitia pointi zilizopangwa (0, 2) na (3,0).

    Unaweza kuangalia kazi yako kwa kupata hatua ya tatu. Tangu mteremko ni\(m=−\frac{2}{3}\), inaweza kuandikwa kama\(m=\frac{2}{-3}\). Rudi nyuma (0,2) na uhesabu kupanda, 2, na kukimbia, -3.

    Zoezi\(\PageIndex{35}\)

    Grafu mstari na y -intercept 4 na mteremko\(m=−\frac{5}{2}\).

    Jibu

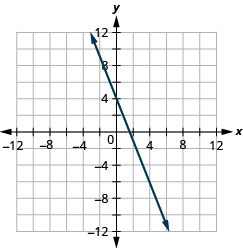
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unachukua mhimili wa y saa (0, 4) na hupita kupitia hatua (4, hasi 6).

    Zoezi\(\PageIndex{36}\)

    Grafu mstari na x -intercept -3 na mteremko\(m=−\frac{3}{4}\).

    Jibu

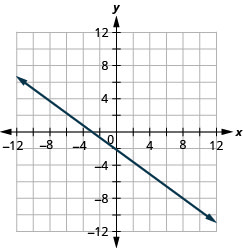
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 12 hadi 12. Mstari unachukua x-axis saa (hasi 3, 0) na hupita kupitia hatua (1, hasi 3).

    Zoezi\(\PageIndex{37}\)

    Grafu mstari unaopitia hatua (-1, 1-3) ambao mteremko wake ni m=4.

    Jibu

    Panda hatua iliyotolewa.

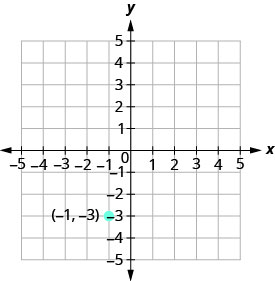
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Hatua (hasi 1, hasi 3) imepangwa na imeandikwa.

    \(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)

    Hesabu kupanda na kukimbia na alama ya pili.

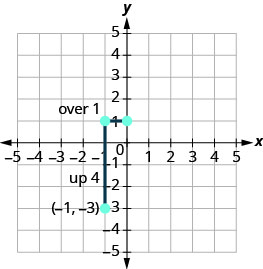
    Takwimu hii inaonyesha jinsi ya kuchora mstari unaopita kupitia hatua (hasi 1, hasi 3) ambao mteremko wake ni 4. Hatua ya kwanza ni kutambua kupanda na kukimbia. Kuongezeka ni 4 na kukimbia ni 1. 4 imegawanywa na 1 ni 4, hivyo mteremko ni 4. Kisha tunahesabu kupanda na kukimbia na alama ya pili. Kwa haki ni grafu ya ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Tunaanza kwenye hatua iliyopangwa (hasi 1, hasi 3) na kuhesabu kupanda, 4. Sisi kufikia hatua hasi 1, 1, ambayo sisi njama. Sisi kisha kuhesabu kukimbia kutoka hatua hii, ambayo ni 1. Tunafikia hatua (0, 1), ambayo imepangwa. Hatua ya mwisho ni kuunganisha pointi mbili na mstari. Tunapata mstari ambao hupita kupitia pointi (hasi 1, hasi 3) na (0, 1).

    Unganisha pointi mbili na mstari.

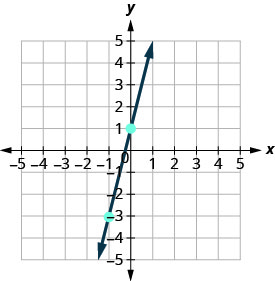
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 5 hadi 5. Mstari unapita kupitia pointi zilizopangwa (-1, -3) na (1,0).

    Unaweza kuangalia kazi yako kwa kupata hatua ya tatu. Kwa kuwa mteremko ni m=4, inaweza kuandikwa kama\(m = \frac{-4}{-1}\). Rudi nyuma (-1, -3) na uhesabu kupanda, -4, na kukimbia, -1.

    Zoezi\(\PageIndex{38}\)

    Grafu mstari na uhakika (-2,1) na mteremko m=3.

    Jibu

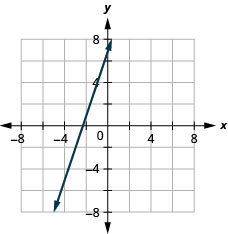
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (hasi 2, 1) na (hasi 1, 4).

    Zoezi\(\PageIndex{39}\)

    Grafu mstari na uhakika (4, -1) na mteremko m=-1.

    Jibu

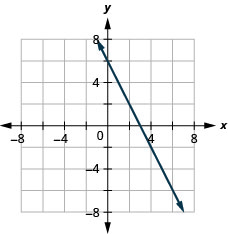
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 7 hadi 7. Mstari unapita kupitia pointi (4, hasi 2) na (5, hasi 4).

    Kutatua Maombi ya mteremko

    Mwanzoni mwa sehemu hii, tulisema kuna maombi mengi ya mteremko katika ulimwengu wa kweli. Hebu tuangalie wachache sasa.

    Zoezi\(\PageIndex{40}\)

    'Lami' ya paa la jengo ni mteremko wa paa. Kujua lami ni muhimu katika hali ya hewa ambapo kuna theluji nzito. Ikiwa paa ni gorofa mno, uzito wa theluji unaweza kusababisha kuanguka. Je! Mteremko wa paa umeonyeshwa nini?

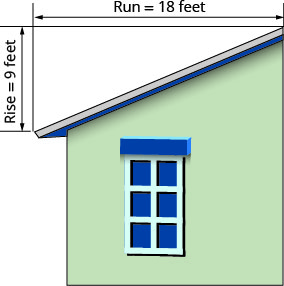
    Takwimu hii inaonyesha nyumba yenye paa la mteremko. Paa juu ya nusu moja ya jengo inaitwa “lami ya paa”. Kuna sehemu ya mstari na mishale kila mwisho kupima urefu wa wima wa paa na inaitwa “kupanda sawa na miguu 9". Kuna sehemu ya mstari na mishale kila mwisho kupima urefu usio na usawa wa mizizi na inaitwa “kukimbia sawa na miguu 18".

    Jibu

    \(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)

    Zoezi\(\PageIndex{41}\)

    Matumizi Zoezi\(\PageIndex{40}\), badala ya kupanda = 14 na kukimbia = 24.

    Jibu

    \(\frac{7}{12}\)

    Zoezi\(\PageIndex{42}\)

    Matumizi Zoezi\(\PageIndex{40}\), badala ya kupanda = 15 na kukimbia = 36.

    Jibu

    \(\frac{5}{12}\)

    Zoezi\(\PageIndex{43}\)

    Je! Umewahi kufikiri juu ya mabomba ya maji taka yanayotoka nyumbani kwako hadi mitaani? Lazima mteremko chini\(\frac{1}{4}\) inchi kwa mguu ili kukimbia vizuri. Je, ni mteremko unaohitajika?

    Takwimu hii ni pembetatu sahihi. Mguu mmoja ni hasi robo moja inchi na mguu mwingine ni mguu mmoja.

    Jibu

    \(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)

    Bomba hupungua inchi 1 kwa kila inchi 48 za kukimbia usawa.

    Zoezi\(\PageIndex{44}\)

    Kupata mteremko wa bomba kwamba mteremko chini\(\frac{1}{3}\) inch kwa mguu.

    Jibu

    \(-\frac{1}{36}\)

    Zoezi\(\PageIndex{45}\)

    Kupata mteremko wa bomba kwamba mteremko chini\(\frac{3}{4}\) inch kwa yadi.

    Jibu

    \(-\frac{1}{48}\)

    Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na kuelewa mteremko wa mstari.

    Dhana muhimu

    • Pata mteremko wa Line kutoka Grafu yake kwa kutumia\(m=\frac{\text { rise }}{\text { run }}\)
      1. Pata pointi mbili kwenye mstari ambao kuratibu ni integers.
      2. Kuanzia na hatua upande wa kushoto, mchoro pembetatu sahihi, kutoka hatua ya kwanza hadi hatua ya pili.
      3. Kuhesabu kupanda na kukimbia kwenye miguu ya pembetatu.
      4. Chukua uwiano wa kupanda ili kukimbia ili kupata mteremko.
    • Grafu Mstari Kutolewa Point na Slope
      1. Panda hatua iliyotolewa.
      2. Tumia formula\(m=\frac{\text { rise }}{\text { run }}\) ya mteremko kutambua kupanda na kukimbia.
      3. Kuanzia kwenye hatua iliyotolewa, uhesabu kupanda na kukimbia ili alama ya pili.
      4. Unganisha pointi kwa mstari.
    • Mteremko wa Mstari wa Ulalo
      • Mteremko wa mstari usio na usawa, y=b, ni 0.
    • Mteremko wa mstari wa wima
      • Mteremko wa mstari wa wima, x=a, haijulikani