Skip to main content
Global

4.3: Grafu na Intercepts

  1. Last updated
  2. Save as PDF
  • Page ID
    177649

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tambua x- na y- intercepts kwenye grafu
    • Kupata x- na y- intercepts kutoka equation ya mstari
    • Graph mstari kwa kutumia intercepts
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kutatua:\(3\cdot 0+4y=−2\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 2.2.13.

    Tambua x - na y - Inakataza kwenye Grafu

    Kila equation linear inaweza kuwakilishwa na mstari wa kipekee ambayo inaonyesha ufumbuzi wote wa equation. Tumeona kwamba wakati wa kuchora mstari kwa kupanga njama, unaweza kutumia ufumbuzi wowote wa tatu kwa grafu. Hii ina maana kwamba watu wawili graphing line wanaweza kutumia seti tofauti ya pointi tatu.

    Kwa mtazamo wa kwanza, mistari yao miwili inaweza kuonekana kuwa sawa, kwani wangekuwa na pointi tofauti zilizoandikwa. Lakini ikiwa kazi yote ilifanyika kwa usahihi, mistari inapaswa kuwa sawa. Njia moja ya kutambua kwamba wao ni kweli mstari huo ni kuangalia ambapo mstari unavuka mstari wa x - mhimili na y - axis. Vipengele hivi huitwa intercepts ya mstari.

    INACHUKULIWA KWA MSTARI

    Vipengele ambapo mstari unavuka mstari wa x - mhimili na y - axis huitwa intercepts ya mstari.

    Hebu tuangalie grafu ya mistari katika Kielelezo\(\PageIndex{1}\).

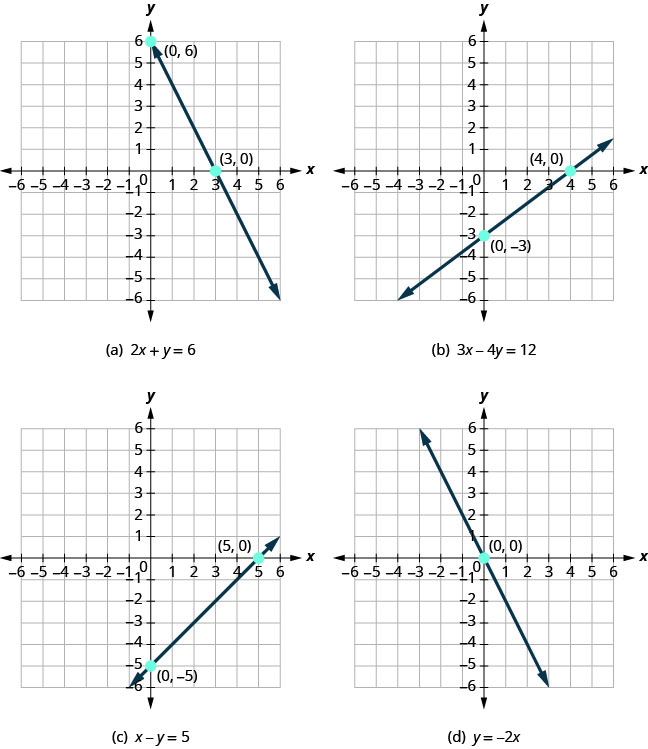
    Takwimu nne, kila kuonyesha tofauti sawa line juu ya x y- kuratibu ndege. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Kielelezo a inaonyesha mstari wa moja kwa moja unaovuka x- mhimili kwenye hatua (3, 0) na kuvuka y- mhimili kwenye hatua (0, 6). Grafu imeandikwa na equation 2x plus y sawa na 6. Kielelezo b inaonyesha mstari wa moja kwa moja unaovuka x- mhimili kwenye hatua (4, 0) na kuvuka y- mhimili kwa uhakika (0, hasi 3). Grafu imeandikwa na equation 3x minus 4y sawa na 12. Kielelezo c inaonyesha mstari wa moja kwa moja unaovuka x- mhimili kwenye hatua (5, 0) na kuvuka y- mhimili kwa uhakika (0, hasi 5). Grafu imeandikwa na equation x minus y sawa na 5. Kielelezo d inaonyesha mstari wa moja kwa moja unaovuka x- mhimili na y- mhimili kwa uhakika (0, 0). Grafu imeandikwa na equation y sawa na 2x hasi.
    Kielelezo\(\PageIndex{1}\): Mifano ya grafu kuvuka mhimili x-hasi.

    Kwanza, angalia ambapo kila moja ya mistari hii huvuka mhimili wa x hasi. Angalia Kielelezo\(\PageIndex{1}\).

    Jedwali\(\PageIndex{1}\)
    Kielelezo Mstari unavuka mstari wa x-axis katika: Amri jozi ya hatua hii
    Kielelezo (a) 3 (3,0)
    Kielelezo (b) 4 (4,0)
    Kielelezo (c) 5 (5,0)
    Kielelezo (d) 0 (0,0)

    Je! Unaona mfano?

    Kwa kila mstari, y - kuratibu ya uhakika ambapo mstari unavuka mstari wa x - ni sifuri. Hatua ambapo mstari unavuka mstari wa x - ina fomu (a,0) na inaitwa x - intercept ya mstari. Kipindi cha x - hutokea wakati y ni sifuri. Sasa, hebu tuangalie pointi ambapo mistari hii inavuka mhimili y. Angalia Jedwali\(\PageIndex{2}\).

    Jedwali\(\PageIndex{2}\)
    Kielelezo Mstari unavuka mstari wa x-axis katika: Amri jozi ya hatua hii
    Kielelezo (a) 6 (0,6)
    Kielelezo (b) 1-3 (0, 1-3)
    Kielelezo (c) -5 (0,5)
    Kielelezo (d) 0 (0,0)

    Je! Ni mfano gani hapa?

    Katika kila mstari, kuratibu x ya uhakika ambapo mstari unavuka y - mhimili ni sifuri. Hatua ambapo mstari unavuka y - mhimili una fomu (0, b) na inaitwa y- intercept ya mstari. Kuzuia y - hutokea wakati x ni sifuri.

    X- KUKATAA NA Y- KUKATAA MSTARI

    Kipindi cha x - ni hatua (a,0) ambapo mstari unavuka mstari wa x - mhimili.

    Y-intercept ni hatua (0, b) ambapo mstari unavuka y - axis.

    Hakuna Nakala ya Alt
    Kielelezo\(\PageIndex{2}\)
    Zoezi\(\PageIndex{1}\)

    Pata x - na y - inakataza kwenye kila grafu.

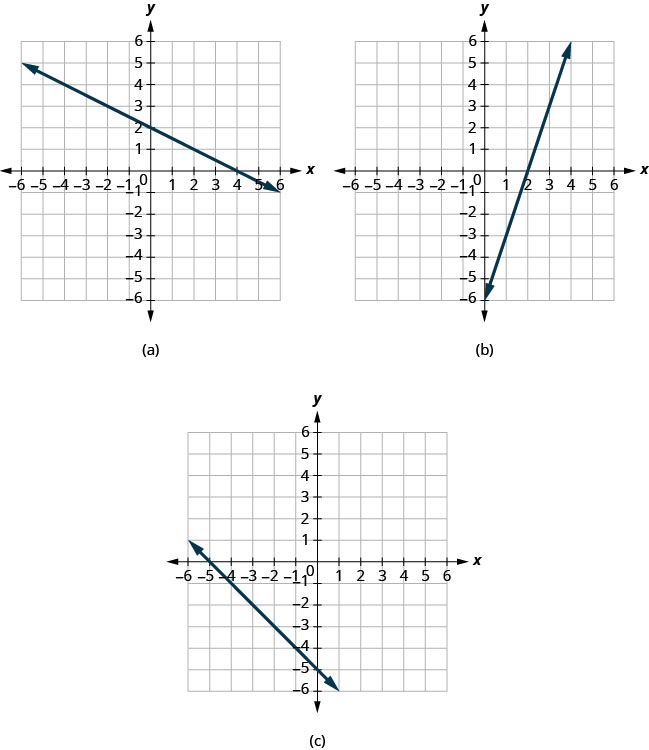
    Takwimu tatu, kila kuonyesha tofauti sawa line juu ya x y- kuratibu ndege. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Kielelezo a inaonyesha mstari wa moja kwa moja kupitia pointi (hasi 6, 5), (hasi 4, 4), (hasi 2, 3), (0, 2), (2, 1), (4, 0), na (6, hasi 1). Kielelezo b inaonyesha mstari wa moja kwa moja kupitia pointi (0, hasi 6), (1, hasi 3), (2, 0), (3, 3), na (4, 6). Kielelezo c inaonyesha mstari wa moja kwa moja unaopitia pointi (hasi 6, 1), (hasi 5, 0), (hasi 4, hasi 1), (hasi 3, hasi 2), (hasi 2, hasi 3), (hasi 1, hasi 4), (0, hasi 5), na (1, hasi 6).
    Kielelezo\(\PageIndex{3}\)
    Jibu

    (a) Grafu huvuka mstari wa x - kwenye hatua (4,0). Kupinga x ni (4,0).
    Grafu huvuka y - mhimili kwa uhakika (0,2). Kuzuia y ni (0,2).

    (b) Grafu huvuka mstari wa x - kwenye hatua (2,0). Kipindi cha x ni (2,0)
    Grafu inavuka y - mhimili kwa uhakika (0, -6). Kuzuia y ni (0, -6).

    (c) Grafu huvuka mstari wa x - kwenye hatua (-5,0). Kupinga x ni (-5,0).
    Grafu inavuka y - mhimili kwa uhakika (0, -5). Kuzuia y ni (0, -5).

    Zoezi\(\PageIndex{2}\)

    Pata x - na y - inakataza kwenye grafu.

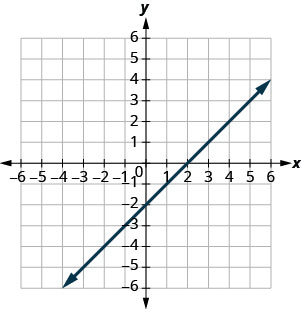
    Takwimu inayoonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili y- wa ndege huendesha kutoka hasi 10 hadi 10. Mstari wa moja kwa moja unapitia pointi (hasi 8, hasi 10), (hasi 6, hasi 8), (hasi 4, hasi 6), (hasi 2, hasi 4), (0, hasi 2), (2, 2), (6, 4), (8, 6), na (10, 8).

    Jibu

    x - kukatiza: (2,0); y - kukatiza: (0, -2)

    Zoezi\(\PageIndex{3}\)

    Pata x - na y - inakataza kwenye grafu.

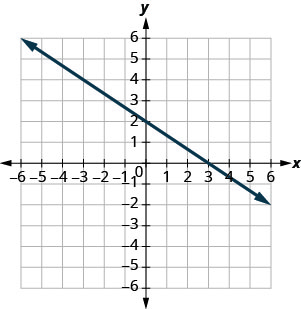
    Takwimu inaonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili y- wa ndege huendesha kutoka hasi 10 hadi 10. Mstari wa moja kwa moja unapitia pointi (hasi 9, 8), (hasi 6, 6), (hasi 3, 4), (0, 2), (3, 0), (6, hasi 2), na (9, hasi 4).

    Jibu

    x - kukatiza: (3,0), y - kukatiza: (0,2)

    Kupata x - na y - Intercepts kutoka Equation ya Line

    Kutambua kwamba x - intercept hutokea wakati y ni sifuri na kwamba y - intercept hutokea wakati x ni sifuri, inatupa njia ya kupata intercepts ya mstari kutoka equation yake. Ili kupata x - intercept, basi y=0 na kutatua kwa x. Ili kupata y - intercept, basi x=0 na kutatua kwa y.

    X- NA Y - INAKABILIWA KUTOKA KWA EQUATION YA MSTARI

    Tumia equation ya mstari. Ili kupata:

    • x - intercept ya mstari, basi y=0 na kutatua kwa x.
    • y - intercept ya mstari, basi x=0 na kutatua kwa y.
    Zoezi\(\PageIndex{4}\)

    Pata intercepts ya 2x+y = 6.

    Jibu

    Tutaruhusu y=0 kupata x - intercept, na basi x=0 kupata y - intercept. Tutajaza meza, ambayo inatukumbusha kile tunachohitaji kupata.

    Takwimu inaonyesha meza yenye safu nne na nguzo mbili. Mstari wa kwanza ni mstari wa kichwa na inaandika meza na equation 2 x plus y sawa 6. Mstari wa pili ni mstari wa kichwa na huandika kila safu. Kichwa cha safu ya kwanza ni “x” na pili ni “y”. Mstari wa tatu umeandikwa “x- intercept” na ina safu ya kwanza tupu na 0 katika safu ya pili. Mstari wa nne umeandikwa “y- intercept” na ina 0 katika safu ya kwanza na safu ya pili tupu.

    Ili kupata x - intercept, basi y=0.

    Jedwali\(\PageIndex{3}\)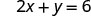
      .
    Hebu y = 0. .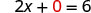
    Kurahisisha. .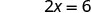
      .
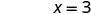
    Ya x -intercept ni (3, 0)
    Ili kupata y -intercept, basi x = 0.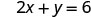  
      .
    Hebu x = 0. .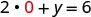
    Kurahisisha. .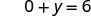
      .
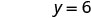
    Y-intercept ni (0, 6)
    Intercepts ni pointi (3,0) na (0,6) kama inavyoonekana katika Jedwali\(\PageIndex{4}\).
    Jedwali\(\PageIndex{4}\)
    2x+y=6
    x y
    3 0
    0 6
    Zoezi\(\PageIndex{5}\)

    Pata intercepts ya 3x+y=12.

    Jibu

    x - kukatiza: (4,0), y - kukatiza: (0,12)

    Zoezi\(\PageIndex{6}\)

    Pata intercepts ya x+4y=8.

    Jibu

    x - kukatiza: (8,0), y - kukatiza: (0,2)

    Zoezi\(\PageIndex{7}\)

    Kupata intercepts ya 4x—3y=12.

    Jibu
    Ili kupata x -intercept, basi y = 0.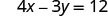  
      .
    Hebu y = 0. .
    Kurahisisha. .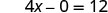
      .
      .
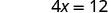
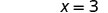
    Ya x -intercept ni (3, 0)
    Ili kupata y -intercept, basi x = 0.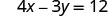  
      .
    Hebu x = 0. .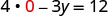
    Kurahisisha. .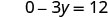
      .
      .
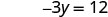
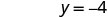
    Y-intercept ni (0, -4)
    Jedwali\(\PageIndex{5}\)

    Intercepts ni pointi (3, 0) na (0, -4) kama inavyoonekana katika meza ifuatayo.

    Jedwali\(\PageIndex{6}\)
    4x-3y=12
    x y
    3 0
    0 -4
    Zoezi\(\PageIndex{8}\)

    Kupata intercepts ya 3x—4y=12.

    Jibu

    x - kukatiza: (4,0), y - kukatiza: (0, 1-3)

    Zoezi\(\PageIndex{9}\)

    Kupata intercepts ya 2x—4y=8.

    Jibu

    x - kukatiza: (4,0), y - kukatiza: (0, -2)

    Grafu Mstari Kutumia Intercepts

    Ili kuchora equation ya mstari kwa pointi za kupanga, unahitaji kupata pointi tatu ambazo kuratibu ni ufumbuzi wa equation. Unaweza kutumia x - na y - intercepts kama mbili ya pointi yako tatu. Pata intercepts, na kisha kupata hatua ya tatu ili kuhakikisha usahihi. Kuhakikisha pointi line up-kisha kuteka line. Njia hii mara nyingi ni njia ya haraka ya kuchora mstari.

    Zoezi\(\PageIndex{10}\): How to Graph a Line Using Intercepts

    Grafu -x+2y=6 kwa kutumia intercepts.

    Jibu

    Takwimu inaonyesha meza na utaratibu wa jumla wa kuchora mstari kwa kutumia intercepts pamoja na mfano maalum kwa kutumia equation hasi x plus 2y sawa 6. Hatua ya 1 ya utaratibu wa jumla ni “Tafuta x na y- intercepts ya mstari. Hebu y sawa 0 na kutatua kwa x. hebu x sawa 0 na kutatua kwa y”. Hatua ya 1 kwa mfano ni mfululizo wa kauli na equations: “Tafuta x- intercept. Hebu y sawa na 0 “, x hasi pamoja na 2y sawa na 6, x hasi pamoja na 2 (0) sawa na 6 (ambapo 0 ni nyekundu), x hasi sawa na 6, x sawa na hasi 6, “X- intercept ni (hasi 6, 0)”, “Tafuta y- intercept. Hebu x sawa 0 “, x hasi pamoja 2y sawa 6, hasi 0 pamoja 2y sawa 6 (ambapo 0 ni nyekundu), 2y sawa 6, y sawa na 3, na “y- kukatiza ni (0, 3)”.Hatua ya 2 ya utaratibu wa jumla ni “Tafuta suluhisho jingine la usawa.” Hatua ya 2 kwa mfano ni mfululizo wa kauli na milinganyo: “Tutatumia x sawa 2”, “Hebu x sawa 2”, hasi x plus 2y sawa 6, hasi 2 pamoja 2y sawa 6 (ambapo kwanza 2 ni nyekundu), 2y sawa 8, y sawa na 4, na “Hatua ya tatu ni (2, 4)”. Hatua ya 3 ya utaratibu wa jumla ni “Panda pointi tatu. 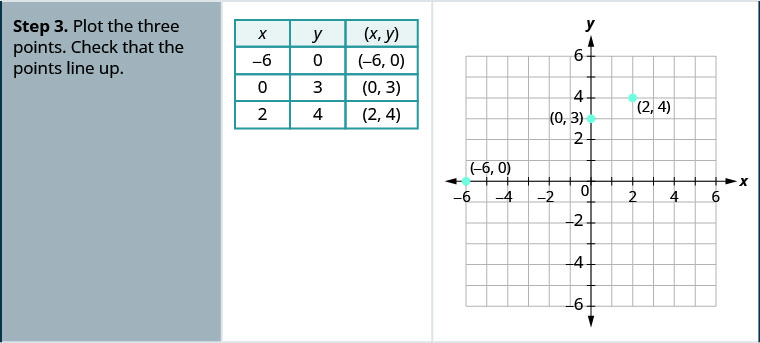Angalia kwamba pointi zinaendelea.”Hatua ya 3 kwa mfano ni meza na grafu. Jedwali lina safu nne na nguzo tatu. Mstari wa kwanza ni mstari wa kichwa na huandika kila safu. Kichwa cha safu ya kwanza ni “x”, ya pili ni “y”, na ya tatu ni “(x, y)”. Chini ya safu ya kwanza ni namba hasi 6, 0 na 2. Chini ya safu ya pili ni namba 0, 3, na 4. Chini ya safu ya tatu ni jozi zilizoamriwa (hasi 6, 0), (0, 3), na (2, 4). Grafu ina pointi tatu kwenye ndege ya kuratibu x- y. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. 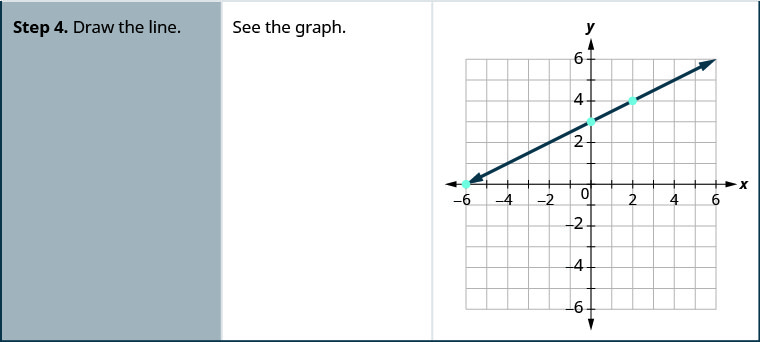Pointi tatu zimewekwa alama (hasi 6, 0), (0, 3), na (2, 4).Hatua ya 4 ya utaratibu wa jumla ni “Chora mstari.” Kwa mfano maalum, kuna taarifa “Angalia grafu” na grafu ya mstari wa moja kwa moja unaopitia pointi tatu kwenye ndege ya kuratibu x y. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Pointi tatu zimewekwa alama (hasi 6, 0), (0, 3), na (2, 4). Mstari wa moja kwa moja hutolewa kupitia pointi (hasi 6, 0), (hasi 4, 1), (hasi 2, 2), (0, 3), (2, 4), (4, 5), na (6, 6).

    Zoezi\(\PageIndex{11}\)

    Grafu x—2y=4 kwa kutumia intercepts.

    Jibu

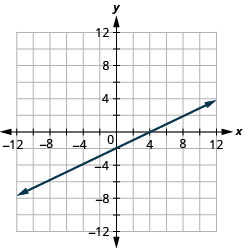
    Takwimu inaonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 12 hadi 12. Mhimili y- wa ndege huendesha kutoka hasi 12 hadi 12. Mstari wa moja kwa moja unapitia pointi (hasi 10, hasi 7), (hasi 8, hasi 6), (hasi 6, hasi 5), (hasi 4, hasi 4), (hasi 2, hasi 3), (0, hasi 2), (2, hasi 1), (4, 0), (6, 1), (8, 2), na (10, 3).

    Zoezi\(\PageIndex{12}\)

    Grafu -x+3y=6 kwa kutumia intercepts.

    Jibu

    Takwimu inaonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 12 hadi 12. Mhimili y- wa ndege huendesha kutoka hasi 12 hadi 12. Mstari wa moja kwa moja unapitia pointi (hasi 12, hasi 2), (hasi 9, hasi 1), (hasi 6, 0), (hasi 3, 1), (0, 2), (3, 3), (6, 4), (9, 5), na (12, 6).

    Hatua za kuchora equation ya mstari kwa kutumia intercepts ni muhtasari hapa chini.

    GRAFU EQUATION LINEAR KWA KUTUMIA INTERCEPTS.
    1. Pata x - na y - intercepts ya mstari.
      • Hebu y=0 na kutatua kwa x
      • Hebu x=0 na kutatua kwa y.
    2. Kupata ufumbuzi wa tatu kwa equation.
    3. Plot pointi tatu na kuangalia kwamba wao line up.
    4. Chora mstari.
    Zoezi\(\PageIndex{13}\)

    Grafu 4x—3y=12 kwa kutumia intercepts.

    Jibu

    Pata intercepts na hatua ya tatu.

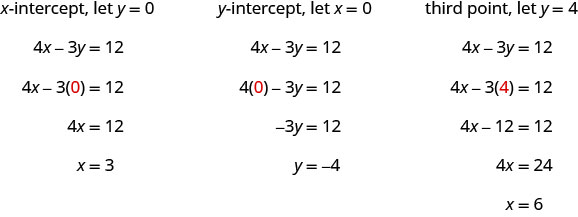
    Takwimu inaonyesha mfululizo wa taarifa na equations: “Pata x- intercept. Hebu y sawa 0 “, 4x bala 3y sawa 12, 4x bala 3 (0) sawa 12 (ambapo 0 ni nyekundu), 4x sawa 12, x sawa 3, “Kupata y- kukatiza. Hebu x sawa 0 “, 4x bala 3y sawa 12, 4 (0) bala 3y sawa 12 (ambapo 0 ni nyekundu), hasi 3y sawa na 12, y sawa hasi 4, “hatua ya tatu, basi y sawa 4”, 4x bala 3y sawa 12, 4x bala 3 (4) sawa 12 (ambapo pili 4 ni nyekundu), 4x minus 12 sawa 12, 4x sawa 24, na x sawa 6.

    Tunaandika pointi katika Jedwali\(\PageIndex{7}\) na kuonyesha grafu hapa chini.

    4x-3y=12
    x y (x, y)
    3 0 (3,0)
    0 -4 (0, -4)
    6 4 (6,4)
    Jedwali\(\PageIndex{7}\)

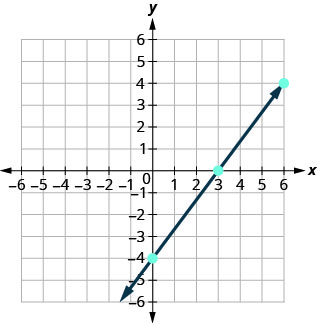
    Takwimu inaonyesha grafu ya mstari wa moja kwa moja kupitia pointi tatu kwenye ndege x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Pointi tatu zimewekwa alama (0, hasi 4), (3, 0), na (6, 4). Mstari wa moja kwa moja hutolewa kupitia pointi (0, hasi 4), (3, 0), na (6, 4).

    Zoezi\(\PageIndex{14}\)

    Grafu 5x—2y=10 kwa kutumia intercepts.

    Jibu

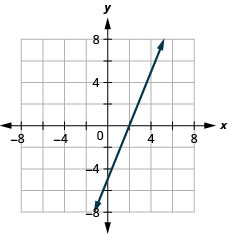
    Takwimu inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Mstari wa moja kwa moja unaendelea kupitia pointi (0, hasi 5), (2, 0), na (4, 5).

    Zoezi\(\PageIndex{15}\)

    Grafu 3x—4y=12 kwa kutumia intercepts.

    Jibu

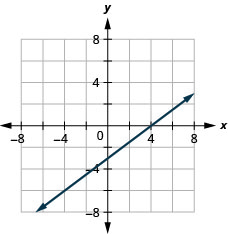
    Takwimu inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 7 hadi 7. Mhimili y- wa ndege huendesha kutoka hasi 7 hadi 7. Mstari wa moja kwa moja unaendelea kupitia pointi (hasi 4, hasi 6), (0, hasi 3), na (4, 0).

    Zoezi\(\PageIndex{16}\)

    Grafu y=5x kutumia intercepts.

    Jibu

    Takwimu inaonyesha seti mbili za taarifa na equations ili kupata intercepts kutoka equation. Seti ya kwanza ya taarifa na equations ni “x- intercept”, “hebu y sawa 0”, y sawa na 5x, 0 sawa na 5x (ambapo 0 ni nyekundu), 0 sawa x, (0, 0). Seti ya pili ya kauli na equations ni “y- intercept”, “basi x sawa 0”, y sawa na 5x, y sawa na 5 (0) (ambapo 0 ni nyekundu), y sawa 0, (0, 0).

    Mstari huu una kizuizi kimoja tu. Ni hatua (0,0).

    Ili kuhakikisha usahihi tunahitaji kupanga njama tatu. Kwa kuwa x - na y - intercepts ni hatua sawa, tunahitaji pointi mbili zaidi kwa grafu mstari.

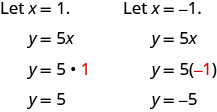
    Takwimu inaonyesha seti mbili za taarifa na equations kupata pointi mbili kutoka equation. Seti ya kwanza ya kauli na milinganyo ni “Hebu x sawa 1”, y sawa na 5x, y sawa na 5 (1) (ambapo 1 ni nyekundu), y sawa na 5. Seti ya pili ya kauli na milinganyo ni “Hebu x sawa na hasi 1”, y sawa na 5x, y sawa na 5 (hasi 1) (ambapo hasi 1 ni nyekundu), y sawa na hasi 5.

    Angalia Jedwali\(\PageIndex{8}\).

    y=5x
    x y (x, y)
        (0,0)
        (1,5)
    -1 -5 (-1, -5)
    Jedwali\(\PageIndex{8}\)

    Panda pointi tatu, angalia kwamba wao line up, na kuteka mstari.

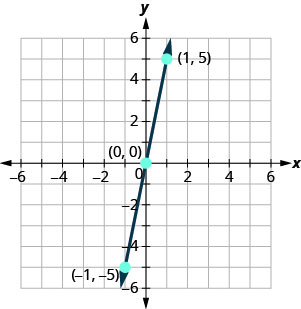
    Takwimu inaonyesha grafu ya mstari wa moja kwa moja kupitia pointi tatu kwenye ndege x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili y- wa ndege huendesha kutoka hasi 10 hadi 10. Pointi tatu zimewekwa alama na zimeandikwa na kuratibu zao (hasi 1, hasi 5), (0, 0), na (1, 5). Mstari wa moja kwa moja hutolewa kupitia pointi (hasi 1, hasi 5), (0, 0), na (1, 5).

    Zoezi\(\PageIndex{17}\)

    Grafu y=4x kutumia intercepts.

    Jibu

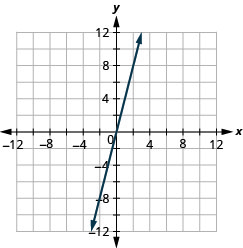
    Takwimu inaonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 12 hadi 12. Mhimili y- wa ndege huendesha kutoka hasi 12 hadi 12. Mstari wa moja kwa moja unapitia pointi (hasi 4, hasi 12), (hasi 3, hasi 9), (hasi 2, hasi 6), (hasi 1, hasi 3), (0, 0), (1, 3), (2, 6), (3, 9), na (4, 12).

    Zoezi\(\PageIndex{18}\)

    Grafu y=-x intercepts.

    Jibu

    Takwimu inaonyesha mstari wa moja kwa moja kwenye ndege ya x y- kuratibu. Mhimili wa x- wa ndege huendesha kutoka hasi 12 hadi 12. Mhimili y- wa ndege huendesha kutoka hasi 12 hadi 12. Mstari wa moja kwa moja hupitia pointi (hasi 10, 10), (hasi 9, 9), (hasi 8, 8), (hasi 7, 7), (hasi 6, 6), (hasi 5, 5), (hasi 4, 4), (hasi 3, 3), (hasi 2, 2), (hasi 1, 2), (3, hasi 3), (4, hasi 4), (5, hasi 5), (6, hasi 6), (7, hasi 7), (8, hasi 8), (9, hasi 9), na (10, hasi 10).

    Dhana muhimu

    • Kupata x - na y - Intercepts kutoka Equation ya Line
      • Tumia equation ya mstari ili kupata x - intercept ya mstari, basi y = 0 na kutatua kwa x.
      • Tumia equation ya mstari ili kupata y - intercept ya mstari, basi x = 0 na kutatua kwa y.
    • Graph Equation Linear kwa kutumia Intercepts
      1. Pata x - na y - intercepts ya mstari.
        Hebu y=0 na kutatua kwa x.
        Hebu x=0 na kutatua kwa y.
      2. Kupata ufumbuzi wa tatu kwa equation.
      3. Plot pointi tatu na kisha kuangalia kwamba wao line up.
      4. Chora mstari.
    • Mkakati wa Kuchagua Njia rahisi zaidi ya Graph Line:
      • Fikiria fomu ya equation.
      • Ikiwa ina variable moja tu, ni mstari wa wima au usawa.
        x=a ni mstari wa wima unaopita kupitia mhimili wa x kwenye
        y=b ni mstari usio na usawa unaopita kupitia mhimili wa y katika b.
      • Ikiwa y imetengwa upande mmoja wa equation, grafu kwa pointi za kupanga.
      • Chagua maadili yoyote matatu kwa x na kisha kutatua kwa y - maadili yanayofanana.
      • Kama equation ni ya fomu ax+by=c, kupata intercepts. Pata x - na y - inakataza na kisha hatua ya tatu.

    faharasa

    intercepts ya mstari
    Vipengele ambapo mstari unavuka mstari wa x - mhimili na y - axis huitwa intercepts ya mstari.
    x - kukatiza
    Hatua (a,0) ambapo mstari unavuka mhimili wa x; x - intercept hutokea wakati y ni sifuri.
    y -kukatiza
    Hatua (0, b) ambapo mstari unavuka y - axis; y - intercept hutokea wakati x ni sifuri.