14.8: Multipliers kubwa

Malengo ya kujifunza

• Tumia njia ya multipliers ya Lagrange kutatua matatizo ya uboreshaji na kikwazo kimoja.
• Tumia njia ya multipliers ya Lagrange kutatua matatizo ya uboreshaji na vikwazo viwili.

Kutatua matatizo ya ufanisi kwa kazi za vigezo viwili au zaidi inaweza kuwa sawa na kutatua matatizo kama hayo katika calculus moja-variable. Hata hivyo, mbinu za kushughulika na vigezo vingi zinatuwezesha kutatua matatizo mbalimbali ya uboreshaji ambayo tunahitaji kukabiliana na hali ya ziada au vikwazo. Katika sehemu hii, tunachunguza njia moja ya kawaida na muhimu ya kutatua matatizo ya ufanisi na vikwazo.

Lagrange multipliers

Katika sehemu iliyopita, hali iliyowekwa ilichunguzwa ikihusisha kuongeza kazi ya faida, chini ya vikwazo fulani. Katika mfano huo, vikwazo vilihusisha idadi kubwa ya mipira ya golf ambayo inaweza kuzalishwa na kuuzwa kwa\(1\) mwezi\((x),\) na idadi kubwa ya masaa ya matangazo ambayo inaweza kununuliwa kwa mwezi\((y)\). Tuseme hizi ziliunganishwa katika kikwazo kimoja cha bajeti, kama vile\(20x+4y≤216\), kwamba alizingatia gharama zote za kuzalisha mipira ya golf na idadi ya masaa ya matangazo kununuliwa kwa mwezi. Lengo bado ni kuongeza faida, lakini sasa kuna aina tofauti ya kikwazo juu ya maadili ya\(x\) na\(y\). Hii kikwazo na kazi sambamba faida

\[f(x,y)=48x+96y−x^2−2xy−9y^2 \nonumber \]

ni mfano wa tatizo optimization, na kazi\(f(x,y)\) inaitwa kazi lengo. Grafu ya curves mbalimbali za ngazi ya kazi\(f(x,y)\) ifuatavyo.

Kielelezo\(\PageIndex{1}\): Grafu kuonyesha curves ngazi ya kazi\(f(x,y)=48x+96y−x^2−2xy−9y^2\) sambamba\(c=150,250,350,\) na\(400.\)

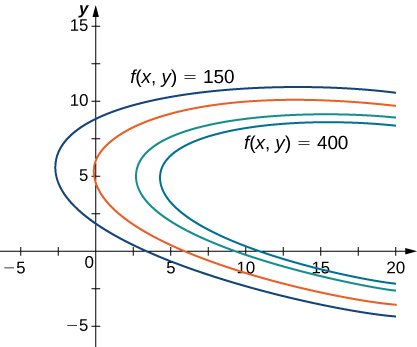
Katika Kielelezo\(\PageIndex{1}\), thamani\(c\) inawakilisha viwango tofauti vya faida (yaani, maadili ya kazi\(f\)). Kama thamani ya\(c\) ongezeko, mabadiliko ya pembe kwa haki. Kwa kuwa lengo letu ni kuongeza faida, tunataka kuchagua Curve mbali na haki iwezekanavyo. Ikiwa hakukuwa na vikwazo juu ya idadi ya mipira ya golf kampuni inaweza kuzalisha au idadi ya vitengo vya matangazo inapatikana, basi tunaweza kuzalisha mipira ya golf kama tunavyotaka, na kutangaza kama vile tunataka, na kutakuwa na faida ya juu kwa kampuni. Kwa bahati mbaya, tuna kikwazo cha bajeti ambacho kinatokana na kukosekana\(20x+4y≤216.\) kwa usawa Ili kuona jinsi kikwazo hiki kinavyoingiliana na kazi ya faida, Kielelezo\(\PageIndex{2}\) kinaonyesha grafu ya mstari\(20x+4y=216\) uliowekwa juu ya grafu ya awali.

Kielelezo\(\PageIndex{2}\): Grafu ya curves ngazi ya kazi\(f(x,y)=48x+96y−x^2−2xy−9y^2\) sambamba\(c=150,250,350,\) na\(395\). Grafu nyekundu ni kazi ya kikwazo.

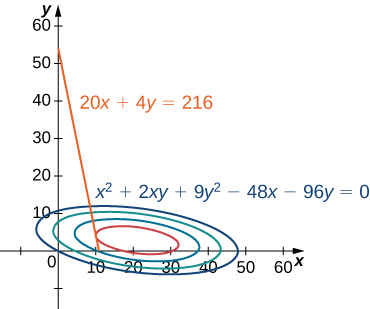
Kama ilivyoelezwa hapo awali, faida ya juu hutokea wakati Curve ya ngazi iko mbali na haki iwezekanavyo. Hata hivyo, kiwango cha uzalishaji sambamba na faida hii ya kiwango cha juu lazima pia kukidhi kikwazo bajeti, hivyo hatua ambayo faida hii hutokea lazima pia uongo juu (au kushoto ya) line nyekundu katika Kielelezo\(\PageIndex{2}\). Ukaguzi wa graph hii inaonyesha kwamba hatua hii ipo ambapo line ni tangent kwa Curve ngazi ya\(f\). Jaribio na hitilafu inaonyesha kwamba ngazi hii ya faida inaonekana kuwa karibu\(395\), wakati\(x\) na wote\(y\) ni chini ya\(5\). Tunarudi kwenye suluhisho la tatizo hili baadaye katika sehemu hii. Kwa upande wa kinadharia, wakati ambapo curve ya faida ni tangent kwa mstari wa kikwazo, gradient ya kazi zote mbili zilizopimwa wakati huo lazima zielekeze katika mwelekeo huo (au kinyume). Kumbuka kwamba gradient ya kazi ya variable zaidi ya moja ni vector. Ikiwa vectors mbili zinaelekeza katika maelekezo sawa (au kinyume), basi mtu lazima awe mara nyingi ya nyingine. Wazo hili ni msingi wa njia ya multipliers ya Lagrange.

Njia ya Multipliers ya Lagrange: Kikwazo kimoja

Theorem\(\PageIndex{1}\): Hebu\(f\) na\(g\) kuwa kazi ya vigezo mbili na derivatives kuendelea sehemu katika kila hatua ya kuweka baadhi ya wazi zenye Curve laini\(g(x,y)=0.\) Tuseme kwamba\(f\), wakati vikwazo kwa pointi juu ya Curve\(g(x,y)=0\), ina extremum ndani katika hatua\((x_0,y_0)\) na hiyo\(\vecs ∇g(x_0,y_0)≠0\). Kisha kuna idadi\(λ\) inayoitwa multiplier Lagrange, ambayo

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0). \nonumber \]

Ushahidi

Kudhani kwamba extremum unakabiliwa hutokea katika hatua\((x_0,y_0).\) Aidha, sisi kudhani kwamba equation\(g(x,y)=0\) inaweza vizuri parameterized kama

\(x=x(s) \; \text{and}\; y=y(s)\)

wapi\(s\) parameter ya urefu wa arc na uhakika\((x_0,y_0)\) wa kumbukumbu\(s=0\). Kwa hiyo, kiasi\(z=f(x(s),y(s))\) kina kiwango cha juu cha jamaa au kiwango cha chini cha jamaa\(s=0\), na hii ina maana kwamba\(\dfrac{dz}{ds}=0\) wakati huo. Kutoka kwa utawala wa mnyororo,

\[\begin{align*} \dfrac{dz}{ds} &=\dfrac{∂f}{∂x}⋅\dfrac{∂x}{∂s}+\dfrac{∂f}{∂y}⋅\dfrac{∂y}{∂s} \\[4pt] &=\left(\dfrac{∂f}{∂x}\hat{\mathbf i}+\dfrac{∂f}{∂y}\hat{\mathbf j}\right)⋅\left(\dfrac{∂x}{∂s}\hat{\mathbf i}+\dfrac{∂y}{∂s}\hat{\mathbf j}\right)\\[4pt] &=0, \end{align*}\]

ambapo derivatives wote ni tathmini katika\(s=0\). Hata hivyo, sababu ya kwanza katika bidhaa dot ni gradient ya\(f\), na sababu ya pili ni kitengo tangent vector\(\vec{\mathbf T}(0)\) kwa Curve kikwazo. Kwa kuwa hatua\((x_0,y_0)\) inalingana na\(s=0\), inafuata kutoka equation hii kwamba

\[\vecs ∇f(x_0,y_0)⋅\vecs{\mathbf T}(0)=0, \nonumber \]

ambayo ina maana kwamba gradient ni ama zero vector\(\vecs 0\) au ni kawaida kwa Curve kikwazo katika kizuizi extremum jamaa. Hata hivyo, Curve kikwazo\(g(x,y)=0\) ni Curve ngazi kwa ajili ya kazi\(g(x,y)\) ili kama\(\vecs ∇g(x_0,y_0)≠0\) basi\(\vecs ∇g(x_0,y_0)\) ni ya kawaida kwa Curve hii katika\((x_0,y_0)\) Ni ifuatavyo, basi, kwamba kuna baadhi scalar\(λ\) vile

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0) \nonumber \]

\(\square\)

Kuomba Theorem\(\PageIndex{1}\) kwa tatizo optimization sawa na ile kwa mtengenezaji mpira wa golf, tunahitaji mkakati wa kutatua matatizo.

Mkakati wa Kutatua matatizo: Hatua za Kutumia Multipliers ya Lagrange

1. Kuamua kazi ya lengo\(f(x,y)\) na kazi ya kikwazo\(g(x,y).\) Je! Tatizo la uboreshaji linahusisha kuongeza au kupunguza kazi ya lengo?
2. Weka mfumo wa equations kwa kutumia template ifuatayo:\[\begin{align} \vecs ∇f(x_0,y_0) &=λ\vecs ∇g(x_0,y_0) \\[4pt] g(x_0,y_0) &=0 \end{align}. \nonumber \]
3. Kutatua kwa\(x_0\) na\(y_0\).
4. Ukubwa wa maadili ya\(f\) ufumbuzi uliopatikana katika hatua\(3\) huongeza\(f\); ndogo zaidi ya maadili hayo hupunguza\(f\).

Mfano\(\PageIndex{1}\): Using Lagrange Multipliers

Tumia njia ya multipliers ya Lagrange ili kupata thamani ya\(f(x,y)=x^2+4y^2−2x+8y\) chini ya chini ya kikwazo\(x+2y=7.\)

Suluhisho

Hebu tufuate mkakati wa kutatua matatizo:

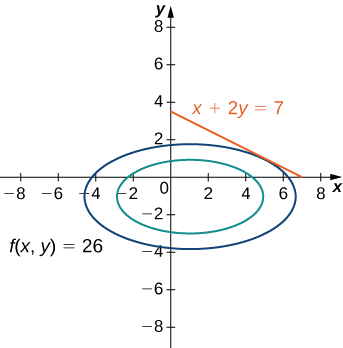
1. Kazi ya lengo ni\(f(x,y)=x^2+4y^2−2x+8y.\) Kuamua kazi ya kikwazo, lazima kwanza tuondoe\(7\) kutoka pande zote mbili za kikwazo. Hii inatoa\(x+2y−7=0.\) kazi kikwazo ni sawa na upande wa kushoto, hivyo\(g(x,y)=x+2y−7\). Tatizo inatuuliza kutatua kwa thamani ya chini ya\(f\), chini ya kikwazo (Kielelezo\(\PageIndex{3}\)).

Kielelezo\(\PageIndex{3}\): Grafu ya curves ngazi ya kazi\(f(x,y)=x^2+4y^2−2x+8y\) sambamba\(c=10\) na\(26\). Grafu nyekundu ni kazi ya kikwazo.

2. Basi tunapaswa kuhesabu gradients ya wote\(f\) na\(g\):

\[\begin{align*} \vecs \nabla f \left( x, y \right) &= \left( 2x - 2 \right) \hat{\mathbf{i}} + \left( 8y + 8 \right) \hat{\mathbf{j}} \\ \vecs \nabla g \left( x, y \right) &= \hat{\mathbf{i}} + 2 \hat{\mathbf{j}}. \end{align*}\]

Equation\(\vecs \nabla f \left( x_0, y_0 \right) = \lambda \vecs \nabla g \left( x_0, y_0 \right)\) inakuwa

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \left( \hat{\mathbf{i}} + 2 \hat{\mathbf{j}} \right), \nonumber \]

ambayo inaweza kuandikwa upya kama

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \hat{\mathbf{i}} + 2 \lambda \hat{\mathbf{j}}. \nonumber \]

Kisha, tunaweka coefficients ya\(\hat{\mathbf{i}}\) na\(\hat{\mathbf{j}}\) sawa na kila mmoja:

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda. \end{align*}\]

Equation\(g \left( x_0, y_0 \right) = 0\) inakuwa\(x_0 + 2 y_0 - 7 = 0\). Kwa hiyo, mfumo wa equations ambayo inahitaji kutatuliwa ni

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda \\ x_0 + 2 y_0 - 7 &= 0. \end{align*}\]

3. Hii ni mfumo wa mstari wa milinganyo mitatu katika vigezo vitatu. Tunaanza kwa kutatua equation ya pili kwa\(λ\) na kuibadilisha kwenye equation ya kwanza. Hii inatoa\(λ=4y_0+4\), hivyo kubadilisha hii katika equation kwanza anatoa\[2x_0−2=4y_0+4.\nonumber \] Kutatua equation hii kwa\(x_0\) anatoa\(x_0=2y_0+3\). Sisi kisha badala hii katika equation ya tatu:

\[\begin{align*} (2y_0+3)+2y_0−7 =0 \\[4pt]4y_0−4 =0 \\[4pt]y_0 =1. \end{align*}\]

Kwa kuwa\(x_0=2y_0+3,\) hii inatoa\(x_0=5.\)

4. Next, sisi kutathmini\(f(x,y)=x^2+4y^2−2x+8y\) katika hatua\((5,1)\),\[f(5,1)=5^2+4(1)^2−2(5)+8(1)=27. \nonumber \] Ili kuhakikisha hii sambamba na thamani ya chini ya kazi kikwazo, hebu kujaribu baadhi ya pointi nyingine juu ya kikwazo kutoka upande wowote wa uhakika\((5,1)\), kama vile intercepts ya\(g(x,y)=0\), ambayo ni\((7,0)\) na\((0,3.5)\).

Tunapata\(f(7,0)=35 \gt 27\) na\(f(0,3.5)=77 \gt 27\).

Kwa hiyo inaonekana kwamba\(f\) ina kiwango cha chini cha\(27\) saa\((5,1)\), chini ya kikwazo kilichopewa.

Zoezi\(\PageIndex{1}\)

Tumia njia ya multipliers Lagrange kupata thamani ya juu ya

\[f(x,y)=9x^2+36xy−4y^2−18x−8y \nonumber \]

chini ya kikwazo\(3x+4y=32.\)

Kidokezo

Tumia mkakati wa kutatua matatizo kwa njia ya multipliers Lagrange.

Jibu

Chini ya kikwazo kilichopewa,\(f\) ina thamani ya juu ya\(976\) wakati\((8,2)\).

Hebu sasa kurudi tatizo lililofanywa mwanzoni mwa sehemu hiyo.

Mfano\(\PageIndex{2}\): Golf Balls and Lagrange Multipliers

Mtengenezaji wa mpira wa golf, Pro-T, ameanzisha mfano wa faida ambayo inategemea idadi\(x\) ya mipira ya golf kuuzwa kwa mwezi (kipimo kwa maelfu), na idadi ya masaa kwa mwezi wa matangazo y, kulingana na kazi

\[z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]

ambapo\(z\) ni kipimo kwa maelfu ya dola. bajeti kikwazo kazi zinazohusiana gharama za uzalishaji wa maelfu golf mipira na vitengo matangazo ni iliyotolewa na\(20x+4y=216.\) Kupata maadili ya\(x\) na\(y\) kwamba kuongeza faida, na kupata faida ya kiwango cha juu.

Suluhisho:

Tena, tunafuata mkakati wa kutatua matatizo:

1. Kazi ya lengo ni\(f(x,y)=48x+96y−x^2−2xy−9y^2.\) Kuamua kazi ya kikwazo, sisi kwanza tunatoa\(216\) kutoka pande zote mbili za kikwazo, kisha ugawanye pande zote mbili na\(4\), ambayo inatoa\(5x+y−54=0.\) Kazi ya kikwazo ni sawa na upande wa kushoto, hivyo\(g(x,y)=5x+y−54.\) Tatizo linatuuliza kutatua upeo wa thamani ya\(f\), chini ya kikwazo hiki.
2. Hivyo, sisi mahesabu gradients ya wote\(f\) na\(g\):\[\begin{align*} \vecs ∇f(x,y) &=(48−2x−2y)\hat{\mathbf i}+(96−2x−18y)\hat{\mathbf j}\\[4pt]\vecs ∇g(x,y) &=5\hat{\mathbf i}+\hat{\mathbf j}. \end{align*}\] equation\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\) inakuwa\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ(5\hat{\mathbf i}+\hat{\mathbf j}),\nonumber \] ambayo inaweza kuandikwa upya kama\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ5\hat{\mathbf i}+λ\hat{\mathbf j}.\nonumber \] Sisi kisha kuweka coefficients ya\(\hat{\mathbf i}\) na\(\hat{\mathbf j}\) sawa na kila mmoja:\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ. \end{align*}\] equation\(g(x_0,y_0)=0\) inakuwa\(5x_0+y_0−54=0\). Kwa hiyo, mfumo wa equations ambayo inahitaji kutatuliwa ni\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ \\[4pt]5x_0+y_0−54 =0. \end{align*}\]
3. Tunatumia upande wa kushoto wa equation pili kuchukua nafasi\(λ\) katika equation kwanza:\[\begin{align*} 48−2x_0−2y_0 &=5(96−2x_0−18y_0) \\[4pt]48−2x_0−2y_0 &=480−10x_0−90y_0 \\[4pt] 8x_0 &=432−88y_0 \\[4pt] x_0 &=54−11y_0. \end{align*}\] Kisha sisi badala hii katika equation tatu:\[\begin{align*} 5(54−11y_0)+y_0−54 &=0\\[4pt] 270−55y_0+y_0-54 &=0\\[4pt]216−54y_0 &=0 \\[4pt]y_0 &=4. \end{align*}\] Kwa kuwa\(x_0=54−11y_0,\) hii inatoa\(x_0=10.\)
4. Sisi kisha mbadala\((10,4)\) katika\(f(x,y)=48x+96y−x^2−2xy−9y^2,\) ambayo inatoa\[\begin{align*} f(10,4) &=48(10)+96(4)−(10)^2−2(10)(4)−9(4)^2 \\[4pt] &=480+384−100−80−144 \\[4pt] &=540.\end{align*}\] Kwa hiyo faida ya kiwango cha juu ambayo yanaweza kupatikana, chini ya vikwazo bajeti, ni\($540,000\) pamoja na kiwango cha uzalishaji wa mipira ya\(10,000\) golf na\(4\) masaa ya matangazo kununuliwa kwa mwezi. Hebu tuangalie ili uhakikishe kuwa hii ni kiwango cha juu. Mwisho wa mstari unaofafanua kikwazo ni\((10.8,0)\) na\((0,54)\) Hebu tathmini\(f\) katika pointi hizi zote mbili: Thamani\[\begin{align*} f(10.8,0) &=48(10.8)+96(0)−10.8^2−2(10.8)(0)−9(0^2) \\[4pt] &=401.76 \\[4pt] f(0,54) &=48(0)+96(54)−0^2−2(0)(54)−9(54^2) \\[4pt] &=−21,060. \end{align*}\] ya pili inawakilisha hasara, kwani hakuna mipira ya golf inayozalishwa. Wala ya maadili haya kisichozidi\(540\), hivyo inaonekana kwamba extremum yetu ni thamani ya juu ya\(f\), chini ya kikwazo fulani.

Zoezi\(\PageIndex{2}\): Optimizing the Cobb-Douglas function

Kampuni imeamua kuwa kiwango chake cha uzalishaji kinatolewa na kazi ya Cobb-Douglas\(f(x,y)=2.5x^{0.45}y^{0.55}\) ambapo\(x\) inawakilisha idadi ya masaa ya kazi kwa\(1\) mwaka na\(y\) inawakilisha jumla ya pembejeo ya mji mkuu kwa kampuni hiyo. Tuseme\(1\) kitengo cha gharama za kazi\($40\) na\(1\) kitengo cha gharama za mji mkuu\($50\). Tumia njia ya multipliers ya Lagrange ili kupata thamani ya juu ya\(f(x,y)=2.5x^{0.45}y^{0.55}\) chini ya kikwazo cha bajeti cha\($500,000\) mwaka.

Kidokezo

Tumia mkakati wa kutatua matatizo kwa njia ya multipliers Lagrange.

Jibu

Chini ya kikwazo kilichopewa, kiwango cha juu cha uzalishaji\(13890\) hutokea kwa masaa ya\(5625\) kazi na\($5500\) ya jumla ya pembejeo ya mji mkuu.

Katika kesi ya kazi lengo na vigezo tatu na kazi moja kikwazo, inawezekana kutumia njia ya Lagrange multipliers kutatua tatizo optimization pia. Mfano wa kazi lengo na vigezo tatu inaweza kuwa Cobb-Douglas kazi katika Zoezi\(\PageIndex{2}\):\(f(x,y,z)=x^{0.2}y^{0.4}z^{0.4},\) ambapo\(x\) inawakilisha gharama ya kazi,\(y\) inawakilisha mji mkuu pembejeo, na\(z\) inawakilisha gharama ya matangazo. Njia hiyo ni sawa na kwa njia na kazi ya vigezo viwili; equations kutatuliwa ni

\[\begin{align*} \vecs ∇f(x,y,z) &=λ\vecs ∇g(x,y,z) \\[4pt] g(x,y,z) &=0. \end{align*}\]

Mfano\(\PageIndex{3}\): Lagrange Multipliers with a Three-Variable objective function

Kuongeza kazi\(f(x,y,z)=x^2+y^2+z^2\) chini ya kikwazo\(x+y+z=1.\)

Suluhisho

1. Kazi ya lengo ni\(f(x,y,z)=x^2+y^2+z^2.\) Kuamua kazi ya kikwazo, tunaondoa\(1\) kutoka kila upande wa kikwazo:\(x+y+z−1=0\) ambayo inatoa kazi ya kikwazo kama\(g(x,y,z)=x+y+z−1.\)

2. Next, sisi mahesabu\(\vecs ∇f(x,y,z)\) na\(\vecs ∇g(x,y,z):\)\[\begin{align*} \vecs ∇f(x,y,z) &=⟨2x,2y,2z⟩ \\[4pt] \vecs ∇g(x,y,z) &=⟨1,1,1⟩. \end{align*}\] Hii inasababisha equations\[\begin{align*} ⟨2x_0,2y_0,2z_0⟩ &=λ⟨1,1,1⟩ \\[4pt] x_0+y_0+z_0−1 &=0 \end{align*}\] ambayo inaweza kuandikwa upya katika fomu ifuatayo:\[\begin{align*} 2x_0 &=λ\\[4pt] 2y_0 &=λ \\[4pt] 2z_0 &=λ \\[4pt] x_0+y_0+z_0−1 &=0. \end{align*}\]

3. Kwa kuwa kila moja ya milinganyo mitatu ya kwanza ina\(λ\) upande wa kulia, tunajua kwamba\(2x_0=2y_0=2z_0\) na vigezo vyote vitatu ni sawa na kila mmoja. Kubadilisha\(y_0=x_0\) na\(z_0=x_0\) katika equation mwisho mavuno\(3x_0−1=0,\) hivyo\(x_0=\frac{1}{3}\)\(y_0=\frac{1}{3}\) na\(z_0=\frac{1}{3}\) ambayo sambamba na hatua muhimu juu ya Curve kikwazo.

4. Kisha, sisi kutathmini\(f\) katika hatua\(\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\):\[f\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2=\dfrac{3}{9}=\dfrac{1}{3} \nonumber \] Kwa hiyo, extremum iwezekanavyo ya kazi ni\(\frac{1}{3}\). Ili kuthibitisha ni kiwango cha chini, chagua pointi zingine zinazotimiza kikwazo kutoka upande wowote wa hatua tuliyopata hapo juu na uhesabu\(f\) kwenye pointi hizo. Kwa mfano,\[\begin{align*} f(1,0,0) &=1^2+0^2+0^2=1 \\[4pt] f(0,−2,3) &=0^2++(−2)^2+3^2=13. \end{align*}\] Wote wa maadili haya ni kubwa kuliko\(\frac{1}{3}\), kutuongoza kuamini extremum ni kiwango cha chini, chini ya kikwazo fulani.

Zoezi\(\PageIndex{3}\)

Tumia njia ya multipliers ya Lagrange ili kupata thamani ya chini ya kazi

\[f(x,y,z)=x+y+z \nonumber \]

chini ya kikwazo\(x^2+y^2+z^2=1.\)

Kidokezo

Tumia mkakati wa kutatua matatizo kwa njia ya multipliers Lagrange na kazi lengo la vigezo tatu.

Jibu

Kutathmini\(f\) katika pointi zote mbili tulipata, inatupa,\[\begin{align*} f\left(\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3}\right) =\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}=\sqrt{3} \\ f\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right) =−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}=−\sqrt{3}\end{align*}\] Tangu kikwazo kinaendelea, tunalinganisha maadili haya na kuhitimisha kwamba\(f\) ina kiwango cha chini cha jamaa cha\(−\sqrt{3}\) wakati\(\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right)\) huo, chini ya kikwazo kilichopewa.

Matatizo na Vikwazo viwili

Njia ya multipliers ya Lagrange inaweza kutumika kwa matatizo na kikwazo zaidi ya moja. Katika kesi hii kazi lengo,\(w\) ni kazi ya vigezo tatu:

\[w=f(x,y,z) \nonumber \]

na ni chini ya vikwazo viwili:

\[g(x,y,z)=0 \; \text{and} \; h(x,y,z)=0. \nonumber \]

Kuna aina mbili multipliers Lagrange\(λ_2\),\(λ_1\) na, na mfumo wa equations inakuwa

\[\begin{align*} \vecs ∇f(x_0,y_0,z_0) &=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0) \\[4pt] g(x_0,y_0,z_0) &=0\\[4pt] h(x_0,y_0,z_0) &=0 \end{align*}\]

Mfano\(\PageIndex{4}\): Lagrange Multipliers with Two Constraints

Pata maadili ya juu na ya chini ya kazi

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

chini ya vikwazo\(z^2=x^2+y^2\) na\(x+y−z+1=0.\)

Suluhisho

Hebu tufuate mkakati wa kutatua matatizo:

1. Kazi ya lengo ni\(f(x,y,z)=x^2+y^2+z^2.\) Kuamua kazi za kikwazo, sisi kwanza huondoa\(z^2\) kutoka pande zote mbili za kikwazo cha kwanza, kinachopa\(x^2+y^2−z^2=0\), hivyo\(g(x,y,z)=x^2+y^2−z^2\). Kazi ya pili ya kikwazo ni\(h(x,y,z)=x+y−z+1.\)
2. Sisi kisha mahesabu gradients ya\(f,g,\) na\(h\):\[\begin{align*} \vecs ∇f(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}+2z\hat{\mathbf k} \\[4pt] \vecs ∇g(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}−2z\hat{\mathbf k} \\[4pt] \vecs ∇h(x,y,z) &=\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}. \end{align*}\] equation\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\) inakuwa\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=λ_1(2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}−2z_0\hat{\mathbf k})+λ_2(\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}), \nonumber \] ambayo inaweza kuandikwa upya kama\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=(2λ_1x_0+λ_2)\hat{\mathbf i}+(2λ_1y_0+λ_2)\hat{\mathbf j}−(2λ_1z_0+λ_2)\hat{\mathbf k}. \nonumber \] Next, sisi kuweka coefficients ya\(\hat{\mathbf i}\) na\(\hat{\mathbf j}\) sawa na kila mmoja:\[\begin{align*}2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2. \end{align*}\] equations mbili yanayotokana na vikwazo ni \(z_0^2=x_0^2+y_0^2\)na\(x_0+y_0−z_0+1=0\). Kuchanganya milinganyo haya na milinganyo mitatu iliyopita inatoa\[\begin{align*} 2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2 \\[4pt]z_0^2 &=x_0^2+y_0^2 \\[4pt]x_0+y_0−z_0+1 &=0. \end{align*}\]
3. Milinganyo mitatu ya kwanza ina variable\(λ_2\). Kutatua equation ya tatu kwa\(λ_2\) na kuchukua nafasi katika equations ya kwanza na ya pili inapunguza idadi ya equations kwa nne:\[\begin{align*}2x_0 &=2λ_1x_0−2λ_1z_0−2z_0 \\[4pt] 2y_0 &=2λ_1y_0−2λ_1z_0−2z_0\\[4pt] z_0^2 &=x_0^2+y_0^2\\[4pt] x_0+y_0−z_0+1 &=0. \end{align*}\] Kisha, sisi kutatua equation ya kwanza na ya pili kwa\(λ_1\). Equation ya kwanza inatoa\(λ_1=\dfrac{x_0+z_0}{x_0−z_0}\), equation ya pili inatoa\(λ_1=\dfrac{y_0+z_0}{y_0−z_0}\). Sisi kuweka upande wa kulia wa kila equation sawa na kila mmoja na msalaba-kuzidisha:\[\begin{align*} \dfrac{x_0+z_0}{x_0−z_0} &=\dfrac{y_0+z_0}{y_0−z_0} \\[4pt](x_0+z_0)(y_0−z_0) &=(x_0−z_0)(y_0+z_0) \\[4pt]x_0y_0−x_0z_0+y_0z_0−z_0^2 &=x_0y_0+x_0z_0−y_0z_0−z_0^2 \\[4pt]2y_0z_0−2x_0z_0 &=0 \\[4pt]2z_0(y_0−x_0) &=0. \end{align*}\] Kwa hiyo, ama\(z_0=0\) au\(y_0=x_0\). Ikiwa\(z_0=0\), basi kikwazo cha kwanza kinakuwa\(0=x_0^2+y_0^2\). tu ufumbuzi halisi ya equation hii ni\(x_0=0\) na\(y_0=0\), ambayo inatoa amri tatu\((0,0,0)\). Hatua hii haina kukidhi kikwazo cha pili, hivyo sio suluhisho. Next, tunaona\(y_0=x_0\), ambayo inapunguza idadi ya equations kwa tatu:\[\begin{align*}y_0 &= x_0 \\[4pt] z_0^2 &= x_0^2 +y_0^2 \\[4pt] x_0 + y_0 -z_0+1 &=0. \end{align*} \nonumber \] Sisi badala equation kwanza katika equations pili na ya tatu:\[\begin{align*} z_0^2 &= x_0^2 +x_0^2 \\[4pt] &= x_0+x_0-z_0+1 &=0. \end{align*} \nonumber \] Kisha, sisi kutatua equation pili kwa\(z_0\), ambayo inatoa\(z_0=2x_0+1\). Sisi kisha badala hii katika equation kwanza,\[\begin{align*} z_0^2 &= 2x_0^2 \\[4pt] (2x_0^2 +1)^2 &= 2x_0^2 \\[4pt] 4x_0^2 + 4x_0 +1 &= 2x_0^2 \\[4pt] 2x_0^2 +4x_0 +1 &=0, \end{align*}\] na kutumia formula quadratic kutatua kwa\(x_0\):\[ x_0 = \dfrac{-4 \pm \sqrt{4^2 -4(2)(1)} }{2(2)} = \dfrac{-4\pm \sqrt{8}}{4} = \dfrac{-4 \pm 2\sqrt{2}}{4} = -1 \pm \dfrac{\sqrt{2}}{2}. \nonumber \] Kumbuka\(y_0=x_0\), hivyo hii kutatua kwa\(y_0\) pia. Kisha\(z_0=2x_0+1\), hivyo\[z_0 = 2x_0 +1 =2 \left( -1 \pm \dfrac{\sqrt{2}}{2} \right) +1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2} . \nonumber \] Kwa hiyo, kuna mbili kuamuru ufumbuzi triplet:\[\left( -1 + \dfrac{\sqrt{2}}{2} , -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) \; \text{and} \; \left( -1 -\dfrac{\sqrt{2}}{2} , -1 -\dfrac{\sqrt{2}}{2} , -1 -\sqrt{2} \right). \nonumber \]
4. Sisi badala\(\left(−1+\dfrac{\sqrt{2}}{2},−1+\dfrac{\sqrt{2}}{2}, −1+\sqrt{2}\right) \) katika\(f(x,y,z)=x^2+y^2+z^2\), ambayo inatoa\[\begin{align*} f\left( -1 + \dfrac{\sqrt{2}}{2}, -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) &= \left( -1+\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 + \dfrac{\sqrt{2}}{2} \right)^2 + (-1+\sqrt{2})^2 \\[4pt] &= \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + (1 -2\sqrt{2} +2) \\[4pt] &= 6-4\sqrt{2}. \end{align*}\] Kisha, sisi badala\(\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2}\right)\) katika\(f(x,y,z)=x^2+y^2+z^2\), ambayo inatoa\[\begin{align*} f\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2} \right) &= \left( -1-\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 - \dfrac{\sqrt{2}}{2} \right)^2 + (-1-\sqrt{2})^2 \\[4pt] &= \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + (1 +2\sqrt{2} +2) \\[4pt] &= 6+4\sqrt{2}. \end{align*}\]\(6+4\sqrt{2}\) ni thamani ya kiwango cha juu na\(6−4\sqrt{2}\) ni thamani ya chini ya\(f(x,y,z)\), chini ya vikwazo kutokana.

Zoezi\(\PageIndex{4}\)

Tumia njia ya multipliers ya Lagrange ili kupata thamani ya chini ya kazi

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

chini ya vikwazo\(2x+y+2z=9\) na\(5x+5y+7z=29.\)

Kidokezo

Tumia mkakati wa kutatua matatizo kwa njia ya multipliers Lagrange na vikwazo viwili.

Jibu

\(f(2,1,2)=9\)ni thamani ya chini ya\(f\), chini ya vikwazo kutokana.

Dhana muhimu

• Kazi ya lengo pamoja na vikwazo moja au zaidi ni mfano wa tatizo la uboreshaji.
• Ili kutatua matatizo ya uboreshaji, tunatumia njia ya multipliers ya Lagrange kutumia mkakati wa kutatua matatizo ya hatua nne.

Mlinganyo muhimu

• Njia ya multipliers Lagrange, kikwazo kimoja

\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\)

\(g(x_0,y_0)=0\)

• Njia ya multipliers Lagrange, vikwazo viwili

\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\)

\(g(x_0,y_0,z_0)=0\)

\(h(x_0,y_0,z_0)=0\)

faharasa

kizuizi

usawa au equation kuwashirikisha vigezo moja au zaidi ambayo hutumiwa katika tatizo optimization; kikwazo inatekeleza kikomo juu ya ufumbuzi iwezekanavyo kwa tatizo

Lagrange multiplier

mara kwa mara (au mara kwa mara) kutumika katika njia ya multipliers Lagrange; katika kesi ya mara kwa mara moja, inawakilishwa na kutofautiana\(λ\)

njia ya multipliers ya Lagrange

njia ya kutatua tatizo optimization chini ya vikwazo moja au zaidi

kazi ya lengo

kazi ambayo ni kuwa maximized au kupunguzwa katika tatizo optimization

tatizo la uboreshaji

hesabu ya thamani ya juu au ya chini ya kazi ya vigezo kadhaa, mara nyingi kwa kutumia multipliers Lagrange