14.8E: Mazoezi ya Sehemu ya 14.8

Last updated
Save as PDF

Page ID: 178674

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1-15, tumia njia ya multipliers ya Lagrange ili kupata maadili ya juu na ya chini ya kazi chini ya kikwazo kilichopewa.

1) Kazi ya lengo:$f(x, y) = 4xy$ Kikwazo:$\dfrac{x^2}{9} + \dfrac{y^2}{16} = 1$

Jibu: $-24$Kwa mujibu wa kikwazo kilichopewa, kazi$f$ ina kiwango cha chini cha jamaa cha wote$ \left(-\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $$ \left(\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $ na kiwango cha juu cha jamaa$24$ kwa wote$ \left(\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $ na$ \left(-\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $

2) Kazi ya lengo:$f(x, y) = x^2y$ Kikwazo:$x^2 + 2y^2 = 6$

3) Kazi ya lengo:$f(x,y)=x^2 +y^2 +2x−2y+1$ Kikwazo:$ g(x,y)= x^2 +y^2 =2 $

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha$-1$ saa$ (-1, 1) $ na kiwango cha juu cha$7$ saa$ (1,-1) $.

4) Kazi ya lengo:$f(x, y) = xy$ Kikwazo:$4x^2 + 8y^2 = 16$

5) Kazi ya lengo:$f(x, y) = x^2 + y^2$ Kikwazo:$xy = 1$

Jibu: $f$ina kiwango cha chini cha jamaa ya$2$ saa zote mbili$ (-1, -1) $ na$ (1,1) $, chini ya kikwazo fulani.

6) Kazi ya lengo:$f(x, y) = x^2 - y^2$ Kikwazo:$x−2y+6=0$

7) Kazi ya lengo:$f(x, y) = x^2 + y^2$ Kikwazo:$x+2y−5=0$

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha jamaa cha$ f(1,2)=5$ wakati huo$ (1, 2) $.

8) Kazi ya lengo:$f(x, y) = x^2 + y^2$ Kikwazo:$(x−1)^2+4y^2=4$

9) Kazi ya lengo:$f(x, y) = 4x^3 + y^2$ Kikwazo:$2x^2 + y^2 = 1$

Jibu: Chini ya kikwazo kilichopewa, kazi$f$ ina kiwango cha chini cha$-\sqrt{2}$ saa$ \left(-\frac{\sqrt{2}}{2}, 0\right) $, kiwango cha chini
cha jamaa cha$\frac{25}{27}$ pointi zote mbili$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $ na$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $,
kiwango cha juu cha$\sqrt{2}$ saa$ \left(\frac{\sqrt{2}}{2}, 0\right) $, na upeo wa jamaa wa $1$katika pointi zote mbili$ (0,1) $ na$ (0,-1) $.

Suluhisho:: Hebu$g(x,y) = 2x^2 + y^2$ iwe kazi ya kikwazo. Kisha:

$\vecs\nabla f(x,y) = 12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$ na Kwa$\vecs\nabla g(x,y) = 4x \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$

kutumia Lagrange multiplier equation,\[\vecs\nabla f(x, y) = \lambda\vecs\nabla g(x, y),\nonumber \]
tuna:\[12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j} = 4x\lambda \, \hat{\mathbf i} + 2y\lambda \,\hat{\mathbf j}\nonumber \]
kutupa mfumo wa equations:\[12x^2 = 4x\lambda, \quad 2y = 2y\lambda, \quad \text{and the constraint}\quad 2x^2 + y^2 = 1\nonumber \]
Kuandika upya kwanza equations mbili kama sifuri bidhaa (kwa kuhamia upande mmoja na factoring), tunapata:
\[\begin{align*} 4x(3x - \lambda) &= 0 & \text{and} && 2y(1 - \lambda) &= 0 \\ x = 0 \quad \text{or}\quad \lambda &= 3x & & &y = 0 \quad \text{or}\quad \lambda &= 1 \end{align*}\]
Sasa tunaona mchanganyiko wa ufumbuzi huu kwa equations mbili hapo juu na kuziba kila moja ya hizi katika equation kikwazo kutatua kwa pointi sambamba Lagrange.

Mchanganyiko$x = 0$ na$y = 0$ hutoa utata wakati umewekwa katika usawa wa kikwazo, kwani hatua hii sio kwenye duaradufu.

Kuchukua mchanganyiko$x = 0$ na$\lambda = 1$, tunaweka$0$$x$ katika kikwazo na kutatua$y$, kupata:$ y = \pm 1$. Hii inatupa pointi mbili Lagrange:$ (0, 1) $ na$ (0, -1)$.

Kuchukua mchanganyiko$\lambda = 3x$ na$y = 0$, tunaweka$0$$y$ katika kikwazo na kutatua$x$, kupata:$ x = \pm \frac{\sqrt{2}}{2}$. Hii inatupa pointi mbili Lagrange:$ \left(-\frac{\sqrt{2}}{2}, 0\right) $ na$ \left(\frac{\sqrt{2}}{2}, 0\right) $.

Kuchukua mchanganyiko$\lambda = 3x$ na$\lambda = 1$, sisi mbadala$1$ katika equation kwanza kwa$\lambda$, kutupa$ 1 = 3x$ hivyo$x = \frac{1}{3}$. Plugging thamani hii katika kwa$x$ katika kikwazo equation na kutatua kwa$y$, sisi kupata$y = \pm \frac{\sqrt{7}}{3}$ ambayo inatupa pointi mbili Lagrange:$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $ na$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $.

Kutathmini kazi$f$ katika pointi hizi za Lagrange, tunaona:\[\begin{align*} f(0, -1) &= 1 & f(0, 1) &= 1 \\ f\left(-\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{-4(\sqrt{2})^3}{8} = -\sqrt{2} & f\left(\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{4(\sqrt{2})^3}{8} = \sqrt{2} \\ f\left(\tfrac{1}{3}, -\tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} & f\left(\tfrac{1}{3}, \tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} \end{align*}\]

Kulinganisha maadili haya na mahali ambapo pointi za Lagrange zinazofanana ziko kwenye safu ya kikwazo, tunahitimisha matokeo yaliyotajwa katika jibu hapo juu.

10) Kazi ya lengo:$f(x,y)=2x^2 +y^2$ Kikwazo:$ g(x,y)= x^2 +y^2 =1 $

11) Kazi ya lengo:$f(x,y,z)=x+3y−z$ Kikwazo:$ x^2+y^2+z^2=4 $

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha jamaa cha$-2\sqrt{11}$ wakati$ \left(-\frac{2\sqrt{11}}{11}, \, -\frac{6\sqrt{11}}{11}, \, \frac{2\sqrt{11}}{11}\right) $ na kiwango cha$2\sqrt{11}$ juu cha jamaa$ \left(\frac{2\sqrt{11}}{11}, \, \frac{6\sqrt{11}}{11}, \, -\frac{2\sqrt{11}}{11}\right).$

12) Kazi ya lengo:$f(x, y, z) = x + y + z$ Kikwazo:$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$

13) Kazi ya lengo:$f(x, y, z) = xyz$ Kikwazo:$x^2+2y^2+3z^2=6$

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha$-\frac{2\sqrt{3}}{3}$ saa$ \left( \sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),$ na$ \left( -\sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right) $ na kiwango cha juu cha$\frac{2\sqrt{3}}{3}$ saa$ \left( \sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),$ na$ \left( -\sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right) $.

14) Kazi ya lengo:$f(x, y, z) = x^2 + y^2 + z^2$ Kikwazo:$x^4+y^4+z^4=1$

15) Kazi ya lengo:$f(x, y, z) = x^2 + y^2 + z^2$ Kikwazo:$xyz=4$

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha jamaa$ 6\sqrt[3]{2}$ katika pointi$ \left(\sqrt[3]{4},\,\sqrt[3]{4},\,\sqrt[3]{4}\right),$$ \left(\sqrt[3]{4},\,-\sqrt[3]{4},\,-\sqrt[3]{4}\right),$$ \left(-\sqrt[3]{4},\,\sqrt[3]{4},\,-\sqrt[3]{4}\right),$ na$ \left(-\sqrt[3]{4},\,-\sqrt[3]{4},\,\sqrt[3]{4}\right).$
Kuona taswira ya 3D ya tatizo hili, angalia: CalcPlot3D kwa Tatizo 15.

Katika mazoezi 16-21, tumia njia ya multipliers ya Lagrange ili kupata extremum iliyoombwa ya kazi iliyotolewa chini ya kikwazo kilichopewa.

16) Kuongeza$f(x,y) = \sqrt{6 - x^2 - y^2}$ chini ya kikwazo,$ x+y−2=0$.

17) Kuongeza$f(x,y) = x^2 - y^2$ chini ya vikwazo,$ g(x,y)=y−x^2=0, \quad x>0,\quad y>0$.

Jibu: Chini ya vikwazo kutokana,$f$ ina upeo jamaa wa$ f\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)=\frac{1}{4}$ katika hatua$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) $. Kama$x > 0$ si kikwazo, kutakuwa na pointi nyingine mbili Lagrange na extrema jamaa ya$f$ chini ya vikwazo vingine viwili. Hizi ingekuwa$ (0, 0) $ na$ \left(-\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) .$

Ili kuthibitisha kwamba$f$ kweli ina upeo jamaa katika hatua$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right), $ tunataka haja ya kuangalia thamani ya$f$ upande wowote wa hatua hii juu ya Curve kikwazo,$y−x^2=0.$

Kama$ x = 0.5$ ambayo ni chini ya$\frac{\sqrt{2}}{2}$,$y$ itakuwa$ y = (0.5)^2 = 0.25.$
Kama$ x = 1$ ambayo ni kubwa kuliko$\frac{\sqrt{2}}{2}$,$y$ itakuwa$ y = (1)^2 = 1.$

Kisha sisi kulinganisha thamani ya $f$katika hatua Lagrange$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)$,, na maadili ya$f$ saa hizi pointi nyingine juu ya kikwazo.
Tuna$f(0.5, 0.25) = (0.5)^2 - (0.25)^2 = 0.25 - 0.0625 = 0.1875 < \frac{1}{4}$ na$f(1, 1) = (1)^2 - (1)^2 = 0 < \frac{1}{4}.$

Kwa hiyo, tunaweza kuhitimisha kwamba kwa$f$ kweli ina upeo jamaa wa$\frac{1}{4}$ katika hatua$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right).$

18) Kuongeza$U(x,y) = 8x^{4/5}y^{1/5}$ chini ya kikwazo,$ 4x+2y=12$.

19) Kupunguza$f(x,y,z)=x^2+y^2+z^2$ chini ya kikwazo,$x+y+z=1$.

Jibu: Chini ya kikwazo kilichopewa,$f$ ina kiwango cha chini cha jamaa cha$ f\left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right)=\frac{1}{3}$ wakati huo$ \left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right) $.

20) Kupunguza$f(x,y)=xy$ juu ya ellipse$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$.

21) Kuongeza$f(x,y,z)=2x+3y+5z$ juu ya nyanja$x^2+y^2+z^2=19$.

Jibu: Chini ya kikwazo kilichopewa,$f$ ina upeo wa jamaa wa$ 19\sqrt{2} $ wakati huo$ \left( \sqrt{2},\, \frac{3\sqrt{2}}{2},\, \frac{5\sqrt{2}}{2} \right) $.
Kumbuka kuwa, chini ya kikwazo hiki,$f$ pia ina kiwango cha chini cha jamaa cha$ -19\sqrt{2} $ wakati huo$ \left( -\sqrt{2},\, -\frac{3\sqrt{2}}{2},\, -\frac{5\sqrt{2}}{2} \right) $.
Ili kuona taswira ya 3D ya tatizo hili, angalia: CalcPlot3D kwa Tatizo 21.

Katika mazoezi 22-23, tumia njia ya multipliers ya Lagrange na vikwazo viwili.

22)$f(x,y,z)=yz+xy$ Ongeza chini ya vikwazo:$xy=1, \quad y^2+z^2=1$.

Jibu: kiwango cha juu:$\frac{3}{2}$, kiwango cha chini:$\frac{1}{2}$

23) Kupunguza$f(x,y,z)=x^2+y^2+z^2$ wakati$x+y+z=9$ na$x+2y+3z=20$.

Jibu: kiwango cha chini:$f(2,3,4)=29$

Tumia njia ya multipliers ya Lagrange kutatua matatizo yafuatayo yaliyotumika.

24) Chombo kikubwa katika sura ya imara ya mstatili lazima iwe na kiasi cha 480 m ³. Chini ya chombo kina gharama $5/m ² ili kujenga wakati juu na pande zina gharama $3/m ² ili kujenga. Tumia multipliers ya Lagrange ili kupata vipimo vya chombo cha ukubwa huu ambacho kina gharama ndogo.

25) Sanduku la mstatili bila ya juu (sanduku la juu) linapaswa kufanywa kutoka 12 ft ² ya kadi. Pata kiasi cha juu cha sanduku kama hilo.

Jibu: Kiwango cha juu ni$4$ ft ³. Vipimo ni$1×2×2$ ft.

26) Kupata umbali wa chini kutoka parabola$y=x^2$ kwa uhakika$(0,3)$.

27) Kupata uhakika juu ya mstari$y=2x+3$ kwamba ni karibu na uhakika$(4,2)$.

Jibu: $ (25,195) $

29) Pata umbali wa chini kutoka hatua$(0,1)$ hadi kwenye parabola$x^2=4y.$

Jibu: $1.0$kitengo

30) Pata umbali wa chini na wa juu kati ya ellipse$x^2+xy+2y^2=1$ na asili.

31) Pata umbali wa chini kutoka ndege$x+y+z=1$ hadi hatua$(2,1,1)$.

Jibu: $\sqrt{3}$vitengo

32) Kupata uhakika juu ya ndege$4x+3y+z=2 $ ambayo ni karibu na uhakika$(1,−1,1)$.

33) Pata uhakika juu ya uso$x^2−2xy+y^2−x+y=0$ karibu na uhakika$(1,2,−3).$

Jibu: $ \left(1,\,\frac{1}{2},\,−3\right) $

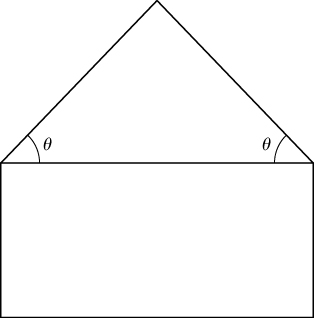
34) Pentagon hutengenezwa kwa kuweka pembetatu ya isosceles kwenye mstatili, kama inavyoonekana kwenye mchoro. Ikiwa mzunguko wa pentagon ni 10 ndani., pata urefu wa pande za pentagon ambayo itaongeza eneo la pentagon.

$CNX_Calc_Figure_14_08_201.jpg$

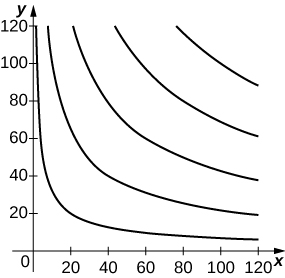
35) [T] Kwa kuwekeza$x$ vitengo vya kazi na$y$ vitengo vya mji mkuu, mtengenezaji wa kuangalia anaweza kuzalisha$P(x,y)=50x^{0.4}y^{0.6}$ saa. Pata idadi kubwa ya saa ambazo zinaweza kuzalishwa kwenye bajeti ya $20,000 ikiwa gharama za kazi $100/kitengo na gharama za mji mkuu $200/kitengo. Tumia grapher kama CalcPlot3D ili mchoro njama ya contour ya kazi.

Jibu

Takriban 3365 saa katika hatua muhimu ($80,60).$

$Mfululizo wa curves katika roboduara ya kwanza, na kuanza kwanza karibu (2, 120), kupungua kwa kasi hadi karibu (20, 20), na kisha kupungua polepole hadi (120, 5). Curve inayofuata huanza karibu (10, 120), inapungua kwa kasi hadi karibu (40, 40), na kisha hupungua polepole hadi (120, 20). Curve inayofuata huanza karibu (20, 120), inapungua kwa kasi hadi karibu (60, 60), na kisha hupungua polepole hadi (120, 40). Curve inayofuata huanza karibu (40, 120), inapungua hadi karibu (80, 80), na kisha hupungua polepole kidogo hadi (120, 60). Curve ya mwisho huanza karibu (60, 120) na inapungua badala sawasawa kupitia (100, 100) hadi (120, 90).$

36) Mango ya mstatili imetolewa ndani ya tetrahedron yenye vipeo$(1,0,0),\,(0,1,0),\,(0,0,1)$, na asili. Msingi wa sanduku una vipimo$x$ na$y$, na urefu wa sanduku ni$z$. Ikiwa jumla ya$x$,$y$, na$z$ ni$1$, pata vipimo vinavyoongeza kiasi cha imara ya mstatili.

37) Pata thamani ya juu ya$f(x,y)=\sin x\sin y,$ wapi$x$ na$y$ ueleze pembe za papo hapo za pembetatu sahihi. Chora njama ya uso na njama ya contour ya kazi kwa kutumia CAS.

Jibu: Chini ya kikwazo hiki,$f$ ina upeo wa jamaa wa$\frac{1}{2}$ wakati$x = \frac{\pi}{4}$ na$y = \frac{\pi}{4}$.
Mpango wa uso na njama ya contour kwa$f$: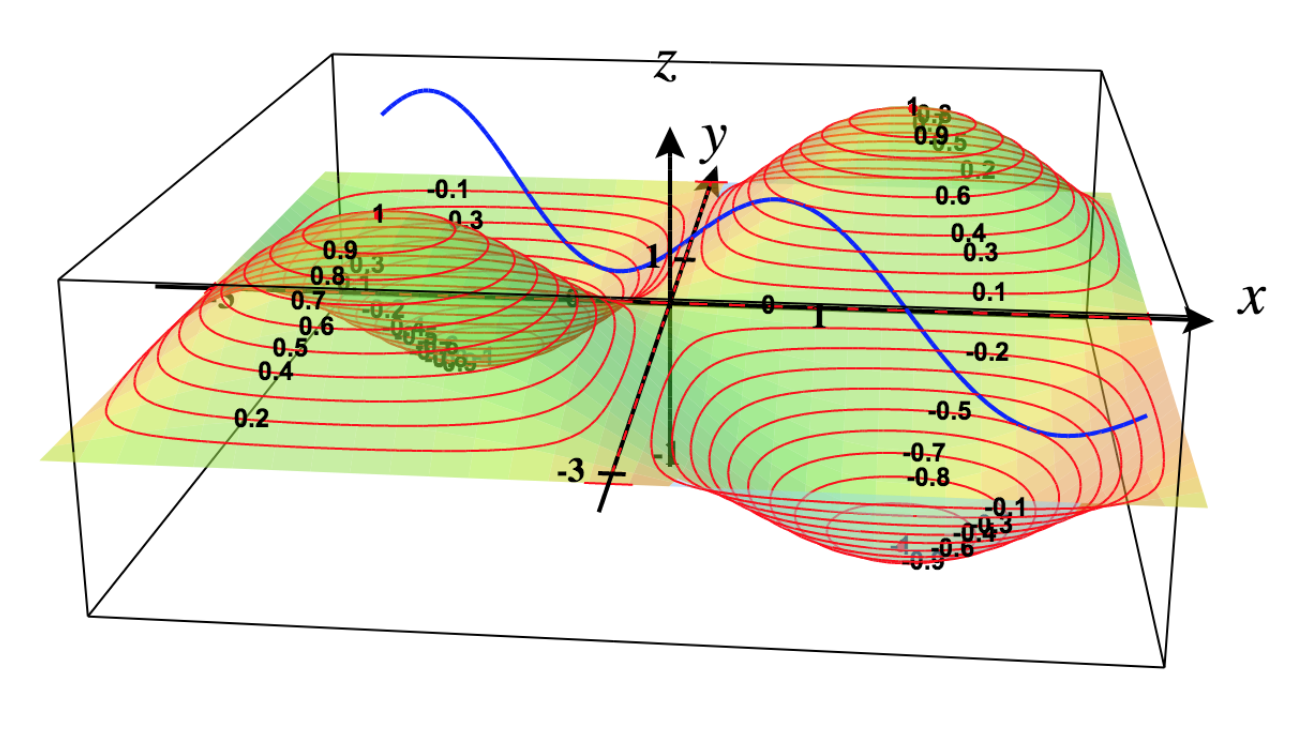
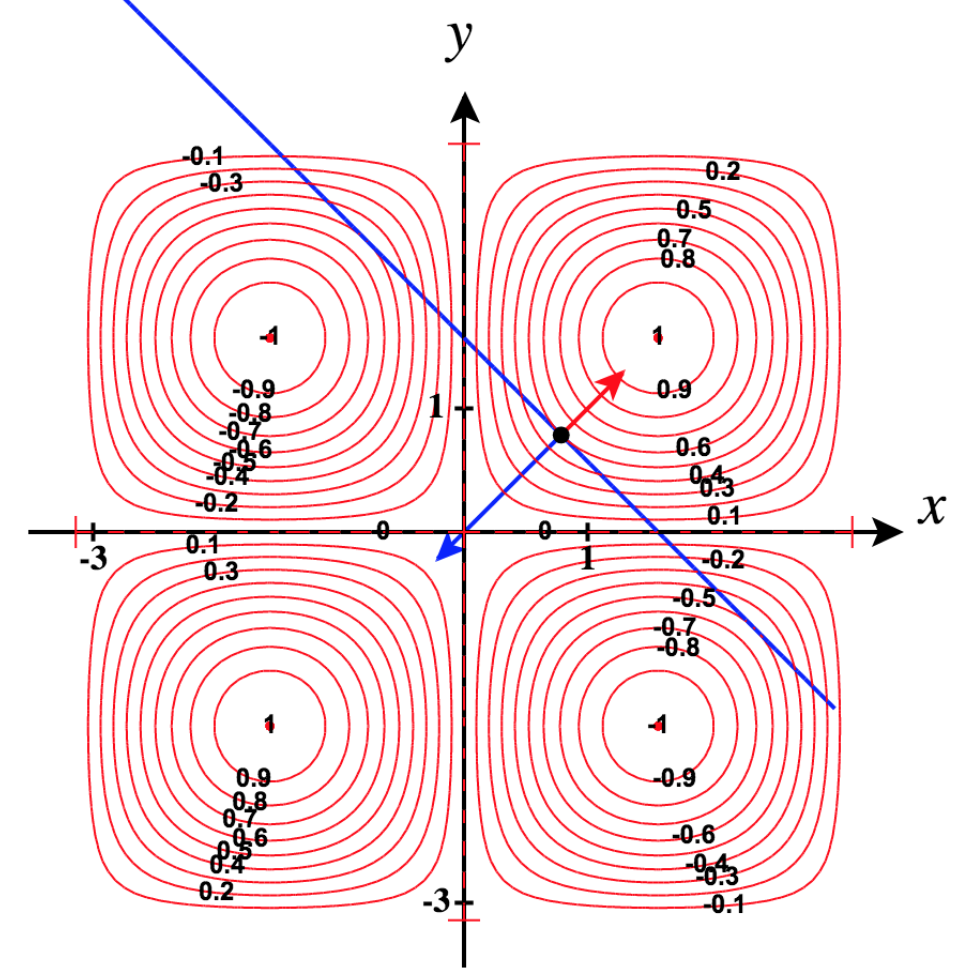
$Mfululizo mbadala wa milima na mabonde ya amplitude 1 katika nafasi ya xyz.$ $Mpango wa contour kwa f (x, y) = dhambi x dhambi y$

38) Onyesha kwamba, ya pembetatu zote zilizoandikwa kwenye mduara wa radius$R$ (angalia mchoro), pembetatu ya equilateral ina mzunguko mkubwa zaidi.

$Mduara wenye pembetatu ya equilateral inayotolewa ndani yake kiasi kwamba kila kipeo cha pembetatu kinagusa mduara.$

Contributors

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) reordered these problems, adding problems 3 and 10 and answers for problems 15 and 17. He also added a full worked-out solution for problem 9 and a link to CalcPlot3D in problems 15, 21 and 35. He also created new images for Problem 37 and expanded the answers for many problems.