14.4: Ndege za Tangent na Makadirio ya mstari

Malengo ya kujifunza

• Kuamua equation ya tangent ndege kwa uso fulani katika hatua.
• Tumia ndege ya tangent ili takriban kazi ya vigezo viwili kwa hatua.
• Eleza wakati kazi ya vigezo viwili ni tofauti.
• Tumia tofauti ya jumla ili takriban mabadiliko katika kazi ya vigezo viwili.

Katika sehemu hii, tunaona tatizo la kutafuta ndege ya tangent kwa uso, ambayo ni sawa na kutafuta equation ya mstari wa tangent kwa Curve wakati Curve inavyoelezwa na grafu ya kazi ya kutofautiana moja,\( y=f(x)\). Mteremko wa mstari wa tangent wakati\( x=a\) huo hutolewa na\( m=f′(a)\); ni mteremko wa ndege ya tangent? Tulijifunza kuhusu usawa wa ndege katika Equations of Lines na Ndege katika Space; katika sehemu hii, tunaona jinsi inaweza kutumika kwa tatizo lililopo.

ndege tangent

Intuitively, inaonekana wazi kwamba, katika ndege, mstari mmoja tu unaweza kuwa tangent kwa curve kwa uhakika. Hata hivyo, katika nafasi tatu-dimensional, mistari mingi inaweza kuwa tangent kwa uhakika fulani. Ikiwa mistari hii iko katika ndege moja, huamua ndege ya tangent wakati huo. Njia ya angavu zaidi ya kufikiria ndege ya tangent ni kudhani uso ni laini wakati huo (hakuna pembe). Kisha, mstari wa tangent kwenye uso wakati huo katika mwelekeo wowote hauna mabadiliko yoyote ya ghafla kwenye mteremko kwa sababu mwelekeo unabadilika vizuri. Kwa hiyo, katika jirani ndogo ya kutosha karibu na hatua hiyo, ndege ya tangent inagusa uso wakati huo tu.

Ufafanuzi: mistari ya tangent

Hebu\( P_0=(x_0,y_0,z_0)\) kuwa hatua juu ya uso\( S\), na basi\( C\) kuwa yoyote Curve kupita kwa njia\( P_0\) na uongo kabisa katika\( S\). Ikiwa mistari ya tangent kwa curves zote hizo\( P_0\) ziko\( C\) kwenye ndege moja, basi ndege hii inaitwa ndege ya tangent kwa\( S\) saa\( P_0\) (Kielelezo\(\PageIndex{1}\)).

Kielelezo\(\PageIndex{1}\): ndege tangent kwa uso\( S\) katika hatua\( P_0\) ina mistari yote tangent kwa curves kwa\(S\) kuwa kupita kwa njia ya\( P_0\).

Kwa ndege ya tangent kwenye uso kuwepo kwa hatua juu ya uso huo, inatosha kwa kazi inayofafanua uso kuwa tofauti wakati huo. Sisi kufafanua mrefu tangent ndege hapa na kisha kuchunguza wazo intuitively.

Ufafanuzi: ndege za tangent

Hebu uso\( S\) inavyoelezwa na kazi differentiable\( z=f(x,y),\) na basi\( P_0=(x_0,y_0)\) kuwa hatua katika uwanja wa\( f\). Kisha, equation ya ndege tangent kwa\( S\) at\( P_0\) ni kutolewa na

\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{tanplane} \]

Ili kuona kwa nini formula hii ni sahihi, hebu kwanza tupate mistari miwili ya tangent kwenye uso\( S\). equation ya mstari tangent kwa Curve kwamba ni kuwakilishwa na makutano ya\( S\) na kufuatilia wima iliyotolewa na\( x=x_0\) ni\( z=f(x_0,y_0)+f_y(x_0,y_0)(y−y_0)\). Vile vile, equation ya mstari tangent kwa Curve kwamba ni kuwakilishwa na makutano ya\( S\) na kufuatilia wima iliyotolewa na\( y=y_0\) ni\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)\). vector sambamba na mstari wa kwanza tangent ni\( \vecs a=\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k}\); vector sambamba na mstari wa pili tangent ni\(\vecs b=\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k}\). Tunaweza kuchukua bidhaa msalaba wa wadudu hawa wawili:

\[\begin{align*} \vecs a\times \vecs b &=(\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k})×(\,\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k})\\[4pt] &=\begin{vmatrix}\hat{\mathbf i} & \hat{\mathbf j} & \hat{\mathbf k}\\[4pt] 0 & 1 & f_y(x_0,y_0)\\[4pt] 1 & 0 & f_x(x_0,y_0)\end{vmatrix} \\[4pt] &=f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}−\,\hat{\mathbf k}. \end{align*}\]

Vector hii ni perpendicular kwa mistari yote na kwa hiyo ni perpendicular kwa ndege tangent. Tunaweza kutumia vector hii kama vector kawaida kwa ndege tangent, pamoja na hatua\( P_0=(x_0,y_0,f(x_0,y_0))\) katika equation kwa ndege:

\[ \begin{align*}\vecs n·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] (f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}-\,\hat{\mathbf k})·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)−(z−f(x_0,y_0)) &=0. \end{align*}\]

Kutatua equation hii kwa\(z\) anatoa Equation\ ref {tanplane}.

Mfano\( \PageIndex{1}\): Finding a Tangent Plane

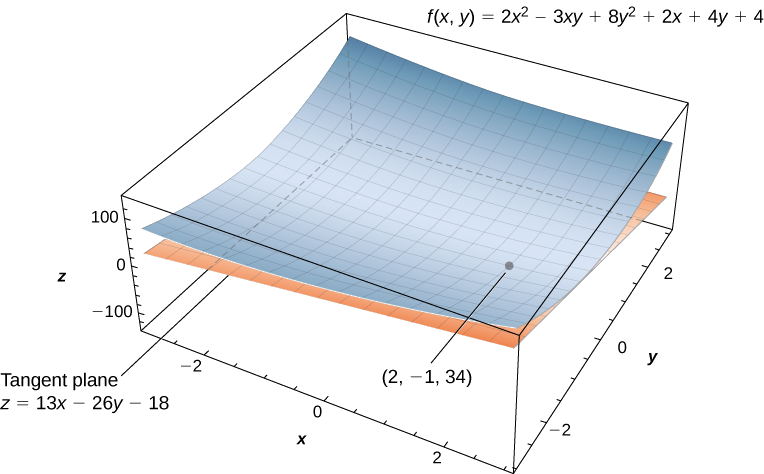
Find equation ya ndege tangent kwa uso defined na kazi\( f(x,y)=2x^2−3xy+8y^2+2x−4y+4\) katika hatua\( (2,−1).\)

Suluhisho

Kwanza, tunapaswa kuhesabu\( f_x(x,y)\) na\( f_y(x,y)\), kisha tumia Equation\( x_0=2\) na\( y_0=−1\):

\[\begin{align*} f_x(x,y) &=4x−3y+2 \\[4pt] f_y(x,y) &=−3x+16y−4 \\[4pt] f(2,−1) &=2(2)^2−3(2)(−1)+8(−1)^2+2(2)−4(−1)+4=34 \\[4pt] f_x(2,−1) &=4(2)−3(−1)+2=13 \\[4pt] f_y(2,−1) &=−3(2)+16(−1)−4=−26.\end{align*}\]

Kisha Equation\ ref {tanplane} inakuwa

\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] z &=34+13(x−2)−26(y−(−1)) \\[4pt] z &=34+13x−26−26y−26 \\[4pt] z &=13x−26y−18. \end{align*}\]

(Angalia takwimu zifuatazo).

Kielelezo\(\PageIndex{2}\): Kuhesabu equation ya ndege tangent kwa uso fulani katika hatua fulani.

Zoezi\( \PageIndex{1}\)

Kupata equation ya ndege tangent kwa uso inavyoelezwa na kazi\( f(x,y)=x^3−x^2y+y^2−2x+3y−2\) katika hatua\( (−1,3)\).

Kidokezo

Kwanza, hesabu\( f_x(x,y)\) na\( f_y(x,y)\), kisha utumie Equation\ ref {tanplane}.

Jibu

\( z=7x+8y−3\)

Mfano\( \PageIndex{2}\): Finding Another Tangent Plane

Find equation ya ndege tangent kwa uso defined na kazi\( f(x,y)=\sin(2x)\cos(3y)\) katika hatua\( (π/3,π/4).\)

Suluhisho

Kwanza, hesabu\( f_x(x,y)\) na\( f_y(x,y)\), kisha utumie Equation\ ref {tanplane} na\( x_0=π/3\) na\( y_0=π/4\):

\[\begin{align*} f_x(x,y) &=2\cos(2x)\cos(3y) \\[4pt] f_y(x,y) &=−3\sin(2x)\sin(3y) \\[4pt] f\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=\sin\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=\left(\dfrac{\sqrt{3}}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\sqrt{6}}{4} \\[4pt] f_x\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=2\cos\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=2\left(−\dfrac{1}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2} \\[4pt] f_y \left(\dfrac{π}{3},\dfrac{π}{4}\right) &=−3\sin\left(2\left(\dfrac{π}{3}\right)\right)\sin\left(3\left(\dfrac{π}{4}\right)\right)=−3\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)=−\dfrac{3\sqrt{6}}{4}. \end{align*}\]

Kisha Equation\ ref {tanplane} inakuwa

\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=−\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{2}\left(x−\dfrac{π}{3}\right)−\dfrac{3\sqrt{6}}{4}\left(y−\dfrac{π}{4}\right) \\[4pt] &=\dfrac{\sqrt{2}}{2}x−\dfrac{3\sqrt{6}}{4}y−\dfrac{\sqrt{6}}{4}−\dfrac{π\sqrt{2}}{6}+\dfrac{3π\sqrt{6}}{16} \end{align*}\]

Ndege ya tangent kwenye uso haipo kila wakati juu ya uso. Fikiria kazi ya kipande

\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases}. \label{oddfunction} \]

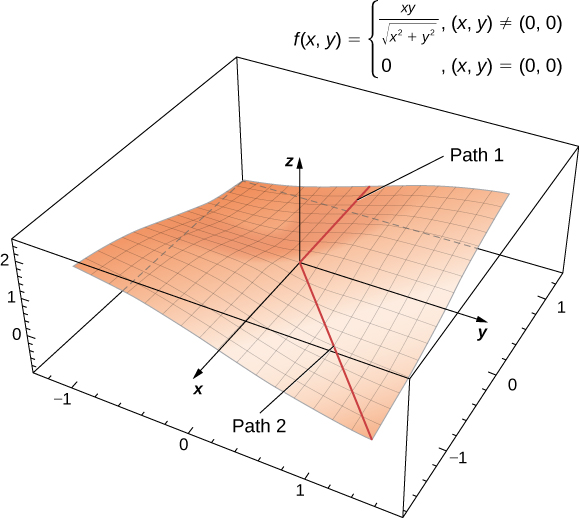
Grafu ya kazi hii ifuatavyo.

Kielelezo\(\PageIndex{3}\): Grafu ya kazi ambayo haina ndege ya tangent katika asili. Takwimu yenye nguvu inayotumiwa na CalcPlot3D.

Ikiwa ama\( x=0\) au\( y=0\),\( f(x,y)=0,\) basi thamani ya kazi haibadilika kwenye aidha\(x\) - au\(y\) - mhimili. Kwa hiyo\( f_x(x,0)=f_y(0,y)=0\), hivyo kama ama\( x\) au\( y\) kufikia sifuri, derivatives hizi za sehemu hukaa sawa na sifuri. Kubadilisha yao katika Equation inatoa\( z=0\) kama equation ya mstari tangent. Hata hivyo, ikiwa tunakaribia asili kutoka kwa mwelekeo tofauti, tunapata hadithi tofauti. Kwa mfano, tuseme tunakaribia asili kando ya mstari\( y=x\). Kama sisi kuweka\( y=x\) katika kazi ya awali, inakuwa

\[f(x,x)=\dfrac{x(x)}{\sqrt{x^2+(x)^2}}=\dfrac{x^2}{\sqrt{2x^2}}=\dfrac{|x|}{\sqrt{2}}. \nonumber \]

Wakati\( x>0,\) mteremko wa Curve hii ni sawa na\( \sqrt{2}/2\); wakati\( x<0\), mteremko wa Curve hii ni sawa na\( −(\sqrt{2}/2).\) Hii inatoa tatizo. Katika ufafanuzi wa ndege ya tangent, tulidhani kwamba mistari yote ya tangent kupitia hatua\( P\) (katika kesi hii, asili) imewekwa katika ndege moja. Hii ni wazi si kesi hapa. Tunapojifunza kazi tofauti, tutaona kwamba kazi hii haijulikani kwa asili.

Makadirio ya mstari

Kumbuka kutoka makadirio Linear na Differentials kwamba formula kwa linear makadirio ya kazi\( f(x)\) katika hatua\( x=a\) inayotolewa na

\[y≈f(a)+f'(a)(x−a). \nonumber \]

Mchoro wa makadirio ya mstari wa kazi ya kutofautiana moja inaonekana kwenye grafu ifuatayo.

Kielelezo\(\PageIndex{4}\): Linear makadirio ya kazi katika variable moja.

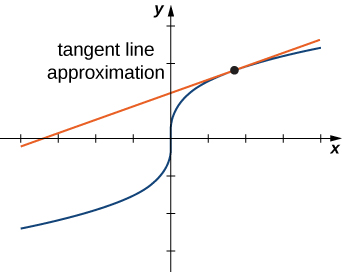
line tangent inaweza kutumika kama makadirio ya kazi\( f(x)\) kwa maadili ya\( x\) sababu karibu na\( x=a\). Wakati wa kufanya kazi na kazi ya vigezo viwili, mstari wa tangent hubadilishwa na ndege ya tangent, lakini wazo la makadirio ni sawa.

Ufafanuzi: Makadirio ya mstari

Kutokana na kazi\( z=f(x,y)\) na derivatives ya sehemu inayoendelea ambayo ipo katika hatua\( (x_0,y_0)\), makadirio ya mstari wa\(f\) wakati\( (x_0,y_0)\) huo hutolewa na equation

\[L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{approx} \]

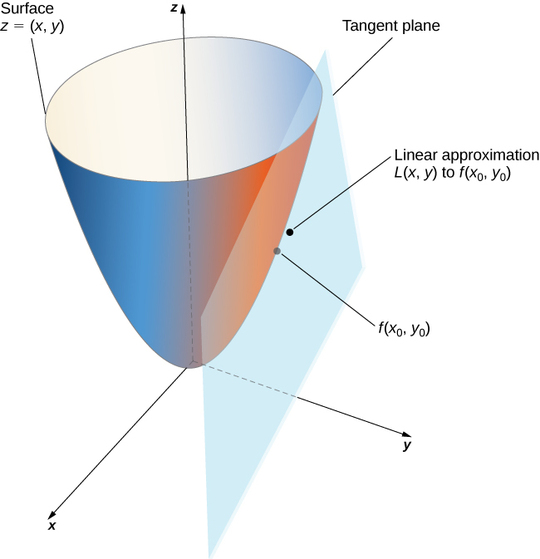
Kumbuka kwamba equation hii pia inawakilisha ndege tangent kwa uso inavyoelezwa na\( z=f(x,y)\) katika hatua\( (x_0,y_0)\). Wazo nyuma ya kutumia makadirio ya mstari ni kwamba, ikiwa kuna\( (x_0,y_0)\) hatua ambayo thamani sahihi ya\( f(x,y)\) inajulikana, basi kwa maadili ya\( (x,y)\) sababu karibu na\( (x_0,y_0)\), makadirio ya mstari (yaani, ndege ya tangent) huzaa thamani ambayo pia ina sababu karibu na thamani halisi ya\( f(x,y)\) (Kielelezo). Zaidi ya hayo, ndege ambayo hutumiwa kupata makadirio linear pia ndege tangent kwa uso katika hatua.\( (x_0,y_0).\)

Kielelezo\(\PageIndex{5}\): Kwa kutumia ndege tangent kwa makadirio linear katika hatua.

Mfano\( \PageIndex{3}\): Using a Tangent Plane Approximation

Kutokana na kazi\( f(x,y)=\sqrt{41−4x^2−y^2}\), takriban\( f(2.1,2.9)\) kutumia uhakika\( (2,3)\) kwa\( (x_0,y_0).\) nini ni thamani ya takriban ya\( f(2.1,2.9)\) sehemu nne decimal?

Suluhisho

Ili kuomba Equation\ ref {takriban}, sisi kwanza lazima tuhesabu\( f(x_0,y_0), f_x(x_0,y_0),\) na\( f_y(x_0,y_0)\) kutumia\( x_0=2\) na\( y_0=3:\)

\[\begin{align*} f(x_0,y_0) &=f(2,3)=\sqrt{41−4(2)^2−(3)^2}=\sqrt{41−16−9}=\sqrt{16}=4 \\[4pt] f_x(x,y) &=−\dfrac{4x}{\sqrt{41−4x^2−y^2}} \text{ so} \; f_x(x_0,y_0)=−\dfrac{4(2)}{\sqrt{41−4(2)^2−(3)^2}}=−2 \\[4pt] f_y(x,y) &=−\dfrac{y}{\sqrt{41−4x^2−y^2}} \text{ so}\; f_y(x_0,y_0)=−\dfrac{3}{\sqrt{41−4(2)^2−(3)^2}}=−\dfrac{3}{4}. \end{align*}\]

Sasa tunabadilisha maadili haya katika Equation\ ref {takriban}:

\[\begin{align*} L(x,y) &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=4−2(x−2)−\dfrac{3}{4}(y−3) \\[4pt] &=\dfrac{41}{4}−2x−\dfrac{3}{4}y. \end{align*}\]

Mwisho, sisi badala\( x=2.1\) na\( y=2.9\) katika\(L(x,y):\)

\[ L(2.1,2.9)=\dfrac{41}{4}−2(2.1)−\dfrac{3}{4}(2.9)=10.25−4.2−2.175=3.875. \nonumber \]

Thamani ya takriban ya\( f(2.1,2.9)\) maeneo manne ya decimal ni

\[ f(2.1,2.9)=\sqrt{41−4(2.1)^2−(2.9)^2}=\sqrt{14.95}≈3.8665, \nonumber \]

ambayo sambamba na\( 0.2%\) makosa katika makadirio.

Zoezi\( \PageIndex{2}\)

Kutokana na kazi\( f(x,y)=e^{5−2x+3y},\) takriban\( f(4.1,0.9)\) kutumia uhakika\( (4,1)\) kwa\( (x_0,y_0)\). Thamani ya takriban ya sehemu nne\( f(4.1,0.9)\) za decimal ni nini?

Kidokezo

Kwanza hesabu\( f(x_0,y_0),f_x(x_0,y_0),\) na\( f_y(x_0,y_0)\) kutumia\( x_0=4\) na\( y_0=1\), halafu utumie Equation\ ref {takriban}.

Jibu

\( L(x,y)=6−2x+3y,\)hivyo\( L(4.1,0.9)=6−2(4.1)+3(0.9)=0.5\)\( f(4.1,0.9)=e^{5−2(4.1)+3(0.9)}=e^{−0.5}≈0.6065.\)

Kutofautisha

Wakati wa kufanya kazi na kazi\( y=f(x)\) ya kutofautiana moja, kazi inasemekana kuwa tofauti katika hatua\( x=a\) ikiwa\( f′(a)\) ipo. Zaidi ya hayo, kama kazi ya kutofautiana moja ni tofauti katika hatua, grafu ni “laini” katika hatua hiyo (yaani, hakuna pembe zipo) na mstari tangent ni vizuri defined katika hatua hiyo.

Wazo nyuma ya kutofautisha kazi ya vigezo viwili ni kushikamana na wazo la urembo katika hatua hiyo. Katika kesi hiyo, uso unachukuliwa kuwa laini wakati huo\( P\) ikiwa ndege ya tangent kwenye uso ipo wakati huo. Ikiwa kazi inatofautiana kwa hatua, basi ndege ya tangent kwenye uso ipo wakati huo. Kumbuka formula (Equation\ ref {tanplane}) kwa ndege tangent katika hatua\( (x_0,y_0)\) ni iliyotolewa na

\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \nonumber \]

Kwa ndege tangent kuwepo katika hatua\( (x_0,y_0),\) hiyo derivatives sehemu hiyo lazima kuwepo katika hatua hiyo. Hata hivyo, hii sio hali ya kutosha kwa urembo, kama ilivyoonyeshwa kwenye Kielelezo. Katika hali hiyo, derivatives ya sehemu ilikuwepo kwa asili, lakini kazi pia ilikuwa na kona kwenye grafu ya asili.

Ufafanuzi: Kazi za kutofautisha

Kazi\( f(x,y)\) ni tofauti katika hatua\( P(x_0,y_0)\) kama, kwa pointi zote\( (x,y)\) katika\( δ\) diski karibu\( P\), tunaweza kuandika

\[f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \label{diff1} \]

ambapo neno la hitilafu\( E\) linatimiza

\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \label{diff2} \]

Muda wa mwisho katika Equation\ ref {diff1} ni kama neno kosa na inawakilisha jinsi karibu ndege tangent inakuja juu ya uso katika jirani ndogo (\( δ\)disk) ya uhakika\( P\). Kwa kazi\( f\) ili kutofautishwa\( P\), kazi lazima iwe laini-yaani, grafu ya\( f\) lazima iwe karibu na ndege ya tangent kwa pointi karibu\( P\).

Mfano\( \PageIndex{4}\): Demonstrating Differentiability

Onyesha kwamba kazi\( f(x,y)=2x^2−4y\) ni tofauti katika hatua\( (2,−3).\)

Suluhisho

Kwanza, tunahesabu\( f(x_0,y_0),f_x(x_0,y_0),\) na\( f_y(x_0,y_0)\) kutumia\( x_0=2\) na\( y_0=−3,\) kisha tunatumia Equation\ ref {diff1}:

\[\begin{align*} f(2,−3) &=2(2)^2−4(−3)=8+12=20 \\[4pt] f_x(2,−3) &=4(2)=8 \\[4pt] f_y(2,−3) &=−4. \end{align*}\]

Kwa hiyo\( m_1=8\) na\( m_2=−4,\) na Equation\ ref {diff1} inakuwa

\[ \begin{align*} f(x,y) &=f(2,−3)+f_x(2,−3)(x−2)+f_y(2,−3)(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8(x−2)−4(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8x−16−4y−12+E(x,y) \\[4pt] 2x^2−4y &=8x−4y−8+E(x,y) \\[4pt] E(x,y) &=2x^2−8x+8. \end{align*}\]

Kisha, tunahesabu kikomo katika Equation\ ref {diff2}:

\ [kuanza {align*}\ lim_ {(x, y) → (x_0, y_0)}\ dfrac {E (x, y)} {\ sqrt {(x-x+0) ^2+ (y-y_0) ^2}}} &=\ lim_ {(x, y) → (2, 1-3)}\ dfrac {2x^2x2 -8x+8} {\ sqrt {(x-1) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, —3)}\ dfrac {2 (x ^ 2,14x+4)} {\ sqrt {(x-1) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, -3)}\ dfrac {2 (x-1) ^2} {\ sqrt {(x ї2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, -3)}\ dfrac {2 (x-1) ^2+ (y+3) ^2)} {\ sqrt {(x-1) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, 1-3)} 2\ sqrt {(x-1) ^2+ (y+3) ^2}\\ [4pt]
&=0. \ mwisho {align*}\]

Tangu\( E(x,y)≥0\) kwa thamani yoyote ya\( x\) au\( y\), kikomo cha awali lazima iwe sawa na sifuri. Kwa hiyo,\( f(x,y)=2x^2−4y\) ni differentiable katika hatua\( (2,−3)\).

Zoezi\( \PageIndex{3}\)

Onyesha kwamba kazi\( f(x,y)=3x−4y^2\) ni tofauti katika hatua\((−1,2)\).

Kidokezo

Kwanza, hesabu\( f(x_0,y_0),f_x(x_0,y_0),\) na\( f_y(x_0,y_0)\) kutumia\( x_0=−1\) na\( y_0=2\), kisha utumie Equation\ ref {diff2} ili upate\( E(x,y)\). Mwisho, hesabu kikomo.

Jibu

\ [kuanza {align*} f (-1,2) &=,119,\ quad f_x (-1,2) =3,\ quad f_y (-1,2) =—16,\ quad E (x, y) =—4 (y-1) ^2.\\ [4pt]
\ lim_ {(x, y) → (x_0, y_0)}\ dfrafram c {E (x, y)} {\ sqrt {(x-x_0) ^2+ (y-y_0) ^2}} &=\ lim_ {(x, y) → (-1,2)}\ dfrac {-4 (y-1) ^2} {\ sqrt {(x+1) ^2+ (y-1) ^2}}\\ [4pt]
&≤\ lim_ {(x, y) → (-1,2)}\ dfrac {-4 (x+1) ^2+ (y-1) ^2)} {\ sqrt {(x+1) ^2+ (y-1) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, -3)} -4\ sqrt {(x+1) ^2+ (y-1) ^2}\\ [4pt]
&=0. \ mwisho {align*}\]

Kazi hii kutoka (Equation\ ref {oddfunction})

\[ f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]

si kutofautisha katika asili (Kielelezo\(\PageIndex{3}\)). Tunaweza kuona hili kwa kuhesabu derivatives ya sehemu. Kazi hii ilionekana mapema katika sehemu, ambapo tulionyesha kuwa\( f_x(0,0)=f_y(0,0)=0\). Kubadilisha habari hii katika equations\ ref {diff1} na\ ref {diff2} kutumia\( x_0=0\) na\( y_0=0\), tunapata

\[\begin{align*} f(x,y) &=f(0,0)+f_x(0,0)(x−0)+f_y(0,0)(y−0)+E(x,y) \\[4pt] E(x,y) &=\dfrac{xy}{\sqrt{x^2+y^2}}. \end{align*}\]

Kuhesabu

\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} \nonumber \]

anatoa

\[\begin{align*} \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} &=\lim_{(x,y)→(0,0)}\dfrac{\dfrac{xy}{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}} \\[4pt] &=\lim_{(x,y)→(0,0)}\dfrac{xy}{x^2+y^2}. \end{align*}\]

Kulingana na njia iliyochukuliwa kuelekea asili, kikomo hiki kinachukua maadili tofauti. Kwa hiyo, kikomo haipo na kazi\( f\) haipatikani kwa asili kama inavyoonekana katika takwimu ifuatayo.

Kielelezo\(\PageIndex{6}\): Kazi hii\( f(x,y)\) (Equation\ ref {oddfunction}) si kutofautishwa katika asili.

Tofauti na kuendelea kwa kazi za vigezo viwili au zaidi vinaunganishwa, sawa na kwa kazi za kutofautiana moja. Kwa kweli, pamoja na marekebisho mengine ya notation, theorem ya msingi ni sawa.

THEOREM: Tofauti Inamaanisha Kuendelea

Hebu\( z=f(x,y)\) kuwa kazi ya vigezo mbili na\( (x_0,y_0)\) katika uwanja wa\( f\). Kama\( f(x,y)\) ni differentiable katika\( (x_0,y_0)\), basi\( f(x,y)\) ni kuendelea katika\( (x_0,y_0).\)

Kumbuka inaonyesha kwamba ikiwa kazi inatofautiana kwa hatua, basi inaendelea huko. Hata hivyo, ikiwa kazi inaendelea kwa hatua, basi sio lazima kutofautishwa wakati huo. Kwa mfano, kazi kujadiliwa hapo juu (Equation\ ref {oddfunction})

\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]

ni kuendelea katika asili, lakini si differentiable katika asili. Uchunguzi huu pia ni sawa na hali katika calculus moja-variable.

Tunaweza zaidi inahusu uhusiano kati ya mwendelezo na kutofautisha katika hatua. Theorem hii inayofuata inasema kwamba ikiwa kazi na derivatives yake ya sehemu zinaendelea kwa hatua, kazi hiyo inatofautiana.

Theorem: Kuendelea kwa Sehemu za Kwanza Inamaanisha kutofautisha

Hebu\( z=f(x,y)\) kuwa kazi ya vigezo mbili na\( (x_0,y_0)\) katika uwanja wa\( f\). Kama\(f(x,y)\),\(f_x(x,y)\), na\(f_y(x,y)\) wote zipo katika jirani ya\((x_0,y_0)\) na ni kuendelea katika\((x_0,y_0)\), basi\(f(x,y)\) ni kutofautishwa huko.

Kumbuka kwamba mapema tulionyesha kuwa kazi katika Equation\ ref {oddfunction} haikutofautishwa kwa asili. Hebu tuhesabu derivatives ya sehemu\( f_x\) na\( f_y\):

\[ \dfrac{∂f}{∂x}=\dfrac{y^3}{(x^2+y^2)^{3/2}} \nonumber \]

na

\[\dfrac{∂f}{∂y}=\dfrac{x^3}{(x^2+y^2)^{3/2}}. \nonumber \]

Mchanganyiko wa theorem iliyotangulia inasema kwamba ikiwa kazi haijulikani, basi angalau moja ya nadharia lazima iwe uongo. Hebu tuchunguze hali ambayo\( f_x(0,0)\) inapaswa kuendelea. Kwa hili kuwa kweli, ni lazima kuwa kweli kwamba

\[ \lim_{(x,y)→(0,0)} f_x(x,y)=f_x(0,0) \nonumber \]

kwa hivyo

\[ \lim_{(x,y)→(0,0)}f_x(x,y)=\lim_{(x,y)→(0,0)}\dfrac{y^3}{(x^2+y^2)^{3/2}}. \nonumber \]

Hebu\( x=ky\). Kisha

\ [kuanza {align*}\ lim_ {(x, y) → (0,0)}\ dfrac {y ^ 3} {(x ^ 2+y ^ 2) ^ {3/2}} &=\ lim_ {y → 0}\ dfrac {y ^ 3} {(y) ^2+y ^ 2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y→ 0}\ dfrac {y ^ 3} {(k ^ 2y ^ 2+y ^ 2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y → 0}\ dfrac {y ^ 3} {|y|^3 (k ^ 2+1) ^ {3/2}}\\ [4pt]
&=\ dfrac {1} (k ^ 2+1) ^ {3/2}}\ lim_ {y → 0}\ dfrac {|y|} {y}. \ mwisho {align*}\]

Ikiwa\( y>0\), basi maneno haya yanafanana\( 1/(k^2+1)^{3/2}\); ikiwa\( y<0\), basi ni sawa\( −(1/(k^2+1)^{3/2})\). Katika hali yoyote, thamani inategemea\( k\), hivyo kikomo kinashindwa kuwepo.

tofauti

Katika Makadirio ya Linear na Differentials sisi kwanza alisoma dhana ya tofauti. Tofauti ya\( y\), imeandikwa\( dy\), inaelezwa kama\( f′(x)dx\). Tofauti hutumiwa kwa takriban\( Δy=f(x+Δx)−f(x)\), wapi\( Δx=dx\). Kupanua wazo hili kwa makadirio linear ya kazi ya vigezo mbili katika hatua\( (x_0,y_0)\) mavuno formula kwa tofauti jumla kwa kazi ya vigezo mbili.

Ufafanuzi: Jumla ya Tofauti

Hebu\( z=f(x,y)\) kuwa kazi ya vigezo mbili na\( (x_0,y_0)\) katika uwanja wa\( f\), na basi\( Δx\) na\( Δy\) kuchaguliwa ili pia\( (x_0+Δx,y_0+Δy)\) ni katika uwanja wa\( f\). Ikiwa\( f\) ni tofauti katika hatua\( (x_0,y_0)\), basi tofauti\( dx\) na\( dy\) hufafanuliwa kama

\[dx=Δx \nonumber \]

na

\[dy=Δy. \nonumber \]

Tofauti\( dz\), pia huitwa tofauti ya jumla ya\( z=f(x,y)\) saa\( (x_0,y_0)\), inaelezwa kama

\[dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \label{total} \]

Kumbuka kwamba ishara\( ∂\) haitumiwi kuashiria tofauti ya jumla; badala,\( d\) inaonekana mbele ya\( z\). Sasa, hebu kufafanua\( Δz=f(x+Δx,y+Δy)−f(x,y).\) Sisi\( dz\) kutumia takriban\( Δz\), hivyo

\[Δz≈dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \nonumber \]

Kwa hiyo, tofauti hutumiwa kukadiria mabadiliko katika kazi\( z=f(x_0,y_0)\)\( (x_0,y_0)\) kwa uhakika wa maadili yaliyotolewa\( Δx\) na\( Δy\). Tangu\( Δz=f(x+Δx,y+Δy)−f(x,y)\), hii inaweza kutumika zaidi kwa takriban\( f(x+Δx,y+Δy):\)

\[ f(x+Δx,y+Δy)=f(x,y)+Δz≈f(x,y)+fx(x_0,y_0)Δx+f_y(x_0,y_0)Δy. \nonumber \]

Angalia takwimu ifuatayo.

Kielelezo\(\PageIndex{7}\): Makadirio ya mstari yanahesabiwa kupitia formula\( f(x+Δx,y+Δy)≈f(x,y)+f_x(x_0,y_0)Δx+f_y(x_0,y_0)Δy.\)

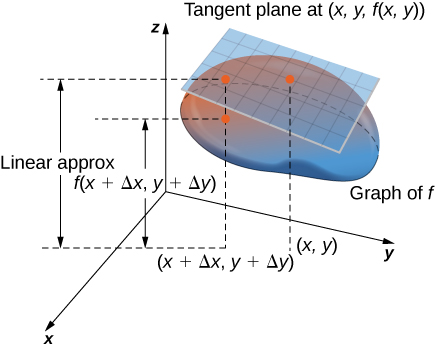
Moja ya matumizi hayo ya wazo hili ni kuamua uenezi wa kosa. Kwa mfano, ikiwa tunatengeneza gadget na tumeondoka kwa kiasi fulani katika kupima kiasi fulani, tofauti inaweza kutumika kukadiria hitilafu kwa kiasi cha jumla cha gadget.

Mfano\( \PageIndex{5}\): Approximation by Differentials

Kupata tofauti\( dz\) ya kazi\( f(x,y)=3x^2−2xy+y^2\) na kuitumia kwa takriban\( Δz\) katika hatua\( (2,−3).\) Matumizi\( Δx=0.1\) na ni thamani halisi ya\( Δy=−0.05.\) nini\( Δz\)?

Suluhisho

Kwanza, tunapaswa kuhesabu\( f(x_0,y_0),f_x(x_0,y_0),\) na\( f_y(x_0,y_0)\) kutumia\( x_0=2\) na\( y_0=−3:\)

\[\begin{align*} f(x_0,y_0) &=f(2,−3)=3(2)^2−2(2)(−3)+(−3)^2=12+12+9=33 \\[4pt] f_x(x,y) &=6x−2y \\[10pt] f_y(x,y) &=−2x+2y \\[4pt] f_x(x_0,y_0) &= fx(2,−3) \\[4pt] &=6(2)−2(−3)=12+6=18 \\[10pt] f_y(x_0,y_0) &=f_y(2,−3) \\[4pt] &=−2(2)+2(−3) \\[4pt] &=−4−6=−10. \end{align*}\]

Kisha, sisi badala ya kiasi hiki katika Equation\ ref {jumla}:

\[\begin{align*} dz &=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy \\[4pt] dz &=18(0.1)−10(−0.05)=1.8+0.5=2.3. \end{align*}\]

Hii ni makadirio\( Δz=f(x_0+Δx,y_0+Δy)−f(x_0,y_0).\) ya thamani halisi ya\( Δz\) hutolewa na

\[\begin{align*} Δz &=f(x_0+Δx,y_0+Δy)−f(x_0,y_0) \\[4pt] &=f(2+0.1,−3−0.05)−f(2,−3) \\[4pt] &=f(2.1,−3.05)−f(2,−3) \\[4pt] &=2.3425. \end{align*}\]

Zoezi\( \PageIndex{4}\)

Pata tofauti\( dz\) ya kazi\( f(x,y)=4y^2+x^2y−2xy\) na uitumie kwa takriban\( Δz\) wakati\( (1,−1)\). Matumizi\( Δx=0.03\) na\( Δy=−0.02\). ni thamani halisi ya\( Δz\) nini?

Kidokezo

Kwanza, hesabu\( f_x(x_0,y_0)\) na\( f_y(x_0,y_0)\) kutumia\( x_0=1\) na\( y_0=−1\), kisha utumie Equation\ ref {jumla}.

Jibu

\( dz=0.18\)

\( Δz=f(1.03,−1.02)−f(1,−1)=0.180682\)

Tofauti ya Kazi ya Vigezo Tatu

Matokeo yote yaliyotangulia ya kutofautisha kazi za vigezo viwili yanaweza kuzalishwa kwa kazi za vigezo vitatu. Kwanza, ufafanuzi:

Ufafanuzi: Differentiability katika hatua

Kazi\( f(x,y,z)\) ni tofauti katika hatua\( P(x_0,y_0,z_0)\) kama kwa pointi zote\( (x,y,z)\) katika\( δ\) diski karibu\( P\) tunaweza kuandika

\[f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z), \nonumber \]

ambapo neno la hitilafu E linatimiza

\[\lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0. \nonumber \]

Ikiwa kazi ya vigezo vitatu inatofautiana kwa hatua\( (x_0,y_0,z_0)\), basi inaendelea huko. Aidha, mwendelezo wa derivatives kwanza sehemu katika hatua hiyo dhamana differentiability

Dhana muhimu

• Analog ya mstari wa tangent kwa curve ni ndege ya tangent kwa uso kwa kazi za vigezo viwili.
• Ndege za tangent zinaweza kutumika kwa maadili ya takriban ya kazi karibu na maadili inayojulikana.
• Kazi ni tofauti katika hatua kama ni “laini” katika hatua hiyo (yaani, hakuna pembe au discontinuities zilizopo katika hatua hiyo).
• Tofauti ya jumla inaweza kutumika kwa takriban mabadiliko katika kazi\( z=f(x_0,y_0)\) kwa uhakika\( (x_0,y_0)\) kwa maadili yaliyotolewa ya\( Δx\) na\( Δy\).

Mlinganyo muhimu

• Tangent ndege

\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

• Ukadiriaji wa mstari

\( L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

• Jumla tofauti

\( dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy\).

• Tofauti (vigezo viwili)

\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)

ambapo neno la hitilafu\( E\) linatimiza

\(\displaystyle \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\).

• Tofauti (vigezo vitatu)

\( f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z),\)

ambapo neno la hitilafu\( E\) linatimiza

\(\displaystyle \lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0\).

faharasa

kutofautishwa

kazi\( f(x,y)\) ni differentiable katika\( (x_0,y_0)\) kama\( f(x,y)\) inaweza kuwa walionyesha katika fomu\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)

ambapo neno la hitilafu\( E(x,y)\) linatimiza\( \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\)

makadirio ya mstari

kutokana na kazi\( f(x,y)\) na ndege ya tangent kwa kazi kwa hatua\( (x_0,y_0)\), tunaweza takriban\( f(x,y)\) kwa pointi karibu na\( (x_0,y_0)\) kutumia formula ya ndege ya tangent

ndege tangent

kutokana na kazi\( f(x,y)\) ambayo inaweza kutofautishwa kwa hatua\( (x_0,y_0)\), usawa wa ndege ya tangent kwenye uso\( z=f(x,y)\) hutolewa na\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)

tofauti ya jumla

tofauti ya jumla ya kazi\( f(x,y)\) katika\( (x_0,y_0)\) hutolewa na formula\( dz=f_x(x_0,y_0)dx+fy(x_0,y_0)dy\)