14.3E: Mazoezi ya Sehemu ya 14.3

Last updated
Save as PDF

Page ID: 178636

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika zoezi zifuatazo, mahesabu derivative sehemu kwa kutumia ufafanuzi kikomo tu.

1)$\dfrac{∂z}{∂y}$ kwa$ z=x^2−3xy+y^2$

Jibu: $\dfrac{∂z}{∂y}=−3x+2y$

Kwa mazoezi 2 - 5, uhesabu ishara ya derivative ya sehemu kwa kutumia grafu ya uso.

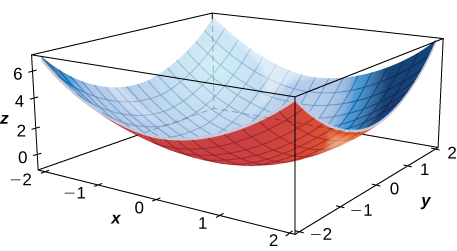
$Mpango wa uso wa paraboloid ambayo ni concave up na ina kipeo chake katika asili$

2)$ f_x(1,1)$

3)$ f_x(−1,1)$

Jibu: Ishara ni hasi.

4)$ f_y(1,1)$

5)$ f_x(0,0)$

Jibu: Derivative ya sehemu ni sifuri katika asili.

Katika mazoezi ya 6 - 16, uhesabu derivatives ya sehemu iliyoombwa.

6)$ \dfrac{∂z}{∂x}$ kwa$ z=\sin(3x)\cos(3y)$

7)$ \dfrac{∂z}{∂y}$ kwa$ z=\sin(3x)\cos(3y)$

Jibu: $ \dfrac{∂z}{∂y}=−3\sin(3x)\sin(3y)$

8)$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$ kwa$ z=x^8e^3y$

9)$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$ kwa$ z=\ln(x^6+y^4)$

Jibu: $ \dfrac{∂z}{∂x}=\frac{6x^5}{x^6+y^4};\quad \dfrac{∂z}{∂y}=\frac{4y^3}{x^6+y^4}$

10)$ f_y(x,y)$ Tafuta$ f(x,y)=e^{xy}\cos(x)\sin(y).$

11) Hebu$ z=e^{xy}.$ Tafuta$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$.

Jibu: $ \dfrac{∂z}{∂x}=ye^{xy};\quad \dfrac{∂z}{∂y}=xe^{xy}$

12) Hebu$ z=\ln(\frac{x}{y})$. Kupata$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$.

13) Hebu$ z=\tan(2x−y).$ Tafuta$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$.

Jibu: $ \dfrac{∂z}{∂x}=2\sec^2(2x−y),\quad \dfrac{∂z}{∂y}=−\sec^2(2x−y)$

14) Hebu$ z=\sinh(2x+3y).$ Tafuta$ \dfrac{∂z}{∂x}$ na$ \dfrac{∂z}{∂y}$.

15) Hebu$ f(x,y)=\arctan(\frac{y}{x}).$ Tathmini$ f_x(2,−2)$ na$ f_y(2,−2)$.

Jibu: $ f_x(2,−2)=\frac{1}{4}=f_y(2,−2)$

16) Hebu$ f(x,y)=\dfrac{xy}{x−y}.$ Tafuta$ f_x(2,−2)$ na$ f_y(2,−2).$

17) Kupata$ \dfrac{∂z}{∂x}$ saa$ (0,1)$ kwa$ z=e^{−x}cos(y)$.

Jibu: $ \dfrac{∂z}{∂x}=−\cos(1)$

18) Kutokana$ \dfrac{∂^2f}{∂x∂y}$ na$ f(x,y,z)=x^3yz^2,$ kupata na$ f_z(1,1,1).$

19) Kutokana$ f(x,y,z)=2\sin(x+y),$ kupata$ f_x(0,\frac{π}{2},−4)$,$f_y(0,\frac{π}{2},−4)$, na$ f_z(0,\frac{π}{2},−4)$.

Jibu: $ f_x(x,y,z)=0,\quad f_y(x,y,z)=0,\quad f_z(x,y,z)=0$

20) Eneo la parallelogram na urefu wa upande wa karibu ambao ni$ a$ na$ b$, na ambapo angle kati ya pande hizi mbili ni$ θ$, hutolewa na kazi$ A(a,b,θ)=ba\sin(θ).$ Pata kiwango cha mabadiliko ya eneo la parallelogram kwa heshima na yafuatayo:

a.$a$

b Upande$b$

c. angle$θ$

21) Eleza kiasi cha silinda ya mviringo ya kulia kama kazi ya vigezo viwili:

a. radius yake$ r$ na urefu wake$ h$.

b Onyesha kwamba kiwango cha mabadiliko ya kiasi cha silinda kuhusiana na radius yake ni bidhaa ya mzunguko wake unaoongezeka kwa urefu wake.

Onyesha kwamba kiwango cha mabadiliko ya kiasi cha silinda kwa heshima na urefu wake ni sawa na eneo la msingi wa mviringo.

Jibu: $ a. V(r,h)=πr^2h$
$ b. \dfrac{∂V}{∂r}=2πrh$
$ c. \dfrac{∂V}{∂h}=πr^2$

22) Fanya mahesabu$ \dfrac{∂w}{∂z}$$ w=z\sin(xy^2+2z).$

Katika mazoezi 23 - 39, tafuta derivatives ya sehemu ya juu ya utaratibu.

23)$ f_{xy}(x,y)$ kwa ajili ya$ f(x,y)=\ln(x−y)$

Jibu: $ f_{xy}(x,y)=\frac{1}{(x−y)^2}$

24)$ f_{yx}(x,y)$ kwa$ f(x, y)=\ln(x−y)$

25) Hebu$ z=x^2+3xy+2y^2.$ Tafuta$ \dfrac{∂^2z}{∂x^2}$ na$ \dfrac{∂^2z}{∂y^2}$.

Jibu: $ \dfrac{∂^2z}{∂x^2}=2,\quad \dfrac{∂^2z}{∂y^2}=4$

26) kutokana$ z=e^x\tan y$, kupata$ \dfrac{∂^2z}{∂x∂y}$ na$ \dfrac{∂^2z}{∂y∂x}$.

27) Kutokana$ f(x,y,z)=xyz,$ kupata$ f_{xyy}(x,y,z),\, f_{yxy}(x,y,z),$ na$ f_{yyx}(x,y,z)$.

Jibu: $ f_{xyy}(x,y,z)=f_{yxy}(x,y,z)=f_{yyx}(x,y,z)=0$

28) Kutokana na$ f(x,y,z)=e^{−2x}\sin(z^2y),$ kuonyesha kwamba$ f_{xyy}(x,y,z)=f_{yxy}(x,y,z)$.

29) Onyesha kwamba$ z=\frac{1}{2}(e^y−e^{−y})\sin x$ ni suluhisho la equation tofauti$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

Jibu: $ \dfrac{d^2z}{dx^2}=−\frac{1}{2}(e^y−e^{−y})\sin x$
$ \dfrac{d^2z}{dy^2}=\frac{1}{2}(e^y−e^{−y})\sin x$
$ \dfrac{d^2z}{dx^2}+\dfrac{d^2z}{dy^2}=0$

30)$ f_{xx}(x,y)$ Tafuta$ f(x,y)=\frac{4x^2}{y}+\frac{y^2}{2x}.$

31) Hebu$ f(x,y,z)=x^2y^3z−3xy^2z^3+5x^2z−y^3z.$ Tafuta$ f_{xyz}.$

Jibu: $ f_{xyz}(x,y,z)=6y^2x−18yz^2$

32) Hebu$ F(x,y,z)=x^3yz^2−2x^2yz+3xz−2y^3z.$ Tafuta$ F_{xyz}(x,y,z)$.

33) Kutokana$ f(x,y)=x^2+x−3xy+y^3−5,$ kupata pointi zote ambazo wakati$ f_x(x,y)=f_y(x,y)=0$ huo huo.

Jibu: $ (\frac{1}{4},\frac{1}{2}),\quad (1,1)$

34) Kutokana$ f(x,y)=2x^2+2xy+y^2+2x−3,$ kupata pointi zote ambazo$ \dfrac{∂f}{∂x}=0$ na$ \dfrac{∂f}{∂y}=0$ wakati huo huo.

35) Kutokana$ f(x,y)=y^3−3yx^2−3y^2−3x^2+1$, kupata pointi zote juu ya ambayo$ f$ wakati$ f_x(x, y)=f_y(x, y)=0$ huo huo.

Jibu: $ (0,0),\quad (0,2),\quad (\sqrt{3},−1), \quad (−\sqrt{3},−1)$

36) Kutokana$ f(x,y)=15x^3−3xy+15y^3,$ kupata pointi zote ambazo wakati$ f_x(x,y)=f_y(x,y)=0$ huo huo.

37) Onyesha kwamba$ z=e^x\sin y$ satisfies equation$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

Jibu: $ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=e^x\sin y−e^x\sin y=0$

38) Onyesha kwamba$ f(x,y)=\ln(x^2+y^2)$ hutatua equation ya Laplace$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

39) Onyesha kwamba$ z=e^{−t}\cos(\frac{x}{c})$ satisfies equation joto$ \dfrac{∂z}{∂t}=−e^{−t}\cos(\frac{x}{c}).$

Jibu: $ c^2\dfrac{∂^2z}{∂x^2}=e^{−t}\cos(\frac{x}{c})$

40)$\displaystyle \lim_{Δx→0}\frac{f(x+Δx)−f(x,y)}{Δx}$ Tafuta$ f(x,y)=−7x−2xy+7y.$

41)$\displaystyle \lim_{Δy→0}\frac{f(x,y+Δy)−f(x,y)}{Δy}$ Tafuta$ f(x,y)=−7x−2xy+7y.$

Jibu: $ \dfrac{∂f}{∂y}=−2x+7$

42)$\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}$ Tafuta$ f(x,y)=x^2y^2+xy+y.$

43)$\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}$ Tafuta$ f(x,y)=\sin(xy).$

Jibu: $ \dfrac{∂f}{∂x}=y\cos xy$

44) Kazi$ P(T,V)=\dfrac{nRT}{V}$ hutoa shinikizo kwa hatua katika gesi kama kazi ya joto$ T$ na kiasi$ V$. Barua$ n$ na$ R$ ni mara kwa mara. Kupata$ \dfrac{∂P}{∂V}$ na$ \dfrac{∂P}{∂T}$, na kueleza nini hizi kiasi kuwakilisha.

45) equation kwa joto kati yake katika$ xy$ -ndege ni$ \dfrac{∂f}{∂t}=\dfrac{∂^2f}{∂x^2}+\dfrac{∂^2f}{∂y^2}$. Onyesha kwamba$ f(x,y,t)=e^{−2t}\sin x\sin y$ ni suluhisho.

46) msingi wimbi equation ni$ f_{tt}=f_{xx}.$ Thibitisha kwamba$ f(x,t)=\sin(x+t)$ na$ f(x,t)=\sin(x−t)$ ni ufumbuzi.

47) Sheria ya cosines inaweza kufikiriwa kama kazi ya vigezo vitatu. Hebu$ x,y,$ na$ θ$ uwe pande mbili za pembetatu yoyote ambapo angle$ θ$ ni angle iliyojumuishwa kati ya pande mbili. Kisha,$ F(x,y,θ)=x^2+y^2−2xy\cos θ$ hutoa mraba wa upande wa tatu wa pembetatu. Pata$ \dfrac{∂F}{∂θ}$ na$ \dfrac{∂F}{∂x}$ lini$ x=2,\,y=3,$ na$ θ=\frac{π}{6}.$

Jibu: $ \dfrac{∂F}{∂θ}=6,\quad \dfrac{∂F}{∂x}=4−3\sqrt{3}$

48) Tuseme pande za mstatili zinabadilika kwa heshima na wakati. Upande wa kwanza unabadilika kwa kiwango cha$ 2$ ndani. /sec ambapo upande wa pili unabadilika kwa kiwango cha$ 4$ katika/sec. Je, ni kasi gani ya mshazari wa mstatili kubadilisha wakati upande wa kwanza$ 16$ unapoingia. na hatua$ 20$ ya pili inaingia. (Jibu la pande zote kwa maeneo matatu ya decimal.)

49) Kazi ya uzalishaji wa Cobb-Douglas ni$ f(x,y)=200x^{0.7}y^{0.3},$ wapi$ x$ na$ y$ kuwakilisha kiasi cha kazi na mtaji unaopatikana. Hebu$ x=500$ na$ y=1000.$ Tafuta$ \dfrac{∂f}{∂x}$ na$ \dfrac{∂f}{∂y}$ kwa maadili haya, ambayo yanawakilisha uzalishaji mdogo wa kazi na mtaji, kwa mtiririko huo.

Jibu: $ \dfrac{∂f}{∂x}$$ (500,1000)=172.36, \quad \dfrac{∂f}{∂y}$katika$ (500,1000)=36.93$

50) Nambari ya joto inayoonekana ni kipimo cha jinsi joto linavyohisi, na inategemea vigezo viwili:$ h$, ambayo ni unyevu wa jamaa, na$ t$, ambayo ni joto la hewa.

$ A=0.885t−22.4h+1.20th−0.544.$Pata$ \dfrac{∂A}{∂t}$ na$ \dfrac{∂A}{∂h}$ lini$ t=20°F$ na$ h=0.90.$