14.3: Derivatives sehemu

Malengo ya kujifunza

• Tumia derivatives ya sehemu ya kazi ya vigezo viwili.
• Tumia derivatives ya sehemu ya kazi ya vigezo zaidi ya mbili.
• Kuamua derivatives ya juu-ili ya kazi ya vigezo viwili.
• Eleza maana ya equation tofauti ya sehemu na kutoa mfano.

Sasa kwa kuwa tumechunguza mipaka na mwendelezo wa kazi za vigezo viwili, tunaweza kuendelea kujifunza derivatives. Kupata derivatives ya kazi ya vigezo viwili ni dhana muhimu katika sura hii, na maombi mengi katika hisabati, sayansi, na uhandisi kama tofauti ya kazi moja-variable. Hata hivyo, tumeona kwamba mipaka na uendelezaji wa kazi nyingi zina masuala mapya na zinahitaji istilahi mpya na mawazo ya kukabiliana nao. Hii hubeba katika upambanuzi pia.

Derivatives ya Kazi ya Vigezo viwili

Wakati wa kusoma derivatives ya kazi ya kutofautiana moja, tuligundua kuwa tafsiri moja ya derivative ni kiwango cha instantaneous ya mabadiliko ya\(y\) kama kazi ya\(x.\) leibniz nukuu kwa derivative ni\(dy/dx,\) ambayo ina maana kwamba\(y\) ni tegemezi variable na\(x\) ni variable huru. Kwa kazi\(z=f(x,y)\) ya vigezo mbili,\(x\) na\(y\) ni vigezo huru na\(z\) ni tegemezi variable. Hii inaibua maswali mawili mara moja: Je, sisi kukabiliana Leibniz nukuu kwa ajili ya kazi ya vigezo mbili? Pia, tafsiri ya derivative ni nini? Jibu liko katika derivatives ya sehemu.

Ufafanuzi: Derivativ

Hebu\(f(x,y)\) kuwa kazi ya vigezo viwili. Kisha derivative sehemu ya kuhusiana\(f\) na\(x\), imeandikwa kama\(∂f/∂x,\), au\(f_x,\) hufafanuliwa kama

\[\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1} \]

derivative sehemu ya kuhusiana\(f\) na\(y\), imeandikwa kama\(∂f/∂y\), au\(f_y,\) hufafanuliwa kama

\[\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2} \]

Ufafanuzi huu unaonyesha tofauti mbili tayari. Kwanza, notation inabadilika, kwa maana kwamba bado tunatumia toleo la maelezo ya Leibniz, lakini\(d\) katika notation ya awali inabadilishwa na ishara\(∂\). (\(“d”\)Mzunguko huu huitwa “sehemu,” hivyo\(∂f/∂x\) huzungumzwa kama “sehemu ya\(f\) kuheshimu\(x\).”) Hii ni ladha ya kwanza kwamba sisi ni kushughulika na derivatives sehemu. Pili, sasa tuna derivatives mbili tofauti tunaweza kuchukua, kwani kuna vigezo viwili tofauti vya kujitegemea. Kulingana na aina gani tunayochagua, tunaweza kuja na derivatives tofauti za sehemu kabisa, na mara nyingi hufanya.

Mfano\(\PageIndex{1}\): Calculating Partial Derivatives from the Definition

Tumia ufafanuzi wa derivative ya sehemu kama kikomo cha kuhesabu\(∂f/∂x\) na\(∂f/∂y\) kwa kazi

\[f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber \]

Suluhisho

Kwanza, mahesabu\(f(x+h,y).\)

\[\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \nonumber \]

Next, badala hii katika Equation\ ref {pd1} na kurahisisha:

\ [kuanza {align*}\ dfrac {f} {x} &=\ lim_ {h → 0}\ dfrac {f (x+h, y) -f (x, y)} {h}\\
&=\ lim_ {h→ 0}\ dfrac {(x ^ 2+2xh+h ^ 2,13xy-3hy+2y ^ 2,14xy+2y ^ 2,14xy+2y -4h+5y-12) - (x ^ 2,13xy+2y ^ 2,14x+5y-12)} {h}\\ &=\ lim_ {h → 0}\ dfrac {x ^ 2+2xy+h ^ 2,13xy-3hy+2y ^ 2+4h+4xy-2+4h+4xy-2+4h+4h+4xy-2+4h+4h+4xy-2+4h+4xy-2+4h+4h+4xy-2+4h+4xy-2+4h+4h+4xy-2+4h+-5y+12} {h}\\
&=\ lim_ {h→ 0}\ dfrac {2 xh+h ^ 2,13h-4h} {h}\\
&=\ lim_ {h → 0}\ dfrac {h (2x+h- 3y-4)} {h}\\
&=\ lim_ {h→ 0} (2x+h-3y-4)\\
&=2x-3y-4. \ mwisho {align*}\]

Ili kuhesabu\(\dfrac{∂f}{∂y}\), kwanza uhesabu\(f(x,y+h):\)

\[\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}\]

Next, badala hii katika Equation\ ref {pd2} na kurahisisha:

\ [kuanza {align*}\ dfrac {f} {y} &=\ lim_ {h → 0}\ dfrac {f (x, y+h) -f (x, y)} {h}\\
&=\ lim_ {h → 0}\ dfrac {(x ^ 2,13xy-3xy+2y ^ 2H+2h ^ 2h+2h ^ 2h+2h ^ 2h+2h^2h+2h ^ 2h+2h^2h+2h ^ 2h+2h^2h+2h ^ 2h+2h^2h+2h ^ 4x+5y+5h-12) - (x ^ 2,13xy+2y ^ 2,14x+5y-12)} {h}\\ &=\ lim_ {h → 0}\ dfrac {x^2,13xy-3xy+2y ^ 2Y^2+4h+2h ^2H^2H^2y ^ 2Y^2y +4x-5y+12} {h}\\
&=\ lim_ {h→ 0}\ dfrac {-3xh+4h+2h ^ 2+5h} {h}\\
&=\ lim_ {h → 0}\ dfrac {h (-3x+4y+2h+5)} {h}\\
&=\ lim_ {h → 0} (-3x+4y+2h+5)\\
&=-3x+4y+5\ mwisho {align*}\]

Zoezi\(\PageIndex{1}\)

Tumia ufafanuzi wa derivative ya sehemu kama kikomo cha kuhesabu\(∂f/∂x\) na\(∂f/∂y\) kwa kazi

\[f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber \]

Kidokezo

Tumia equations\ ref {pd1} na\ ref {pd2} kutoka ufafanuzi wa derivatives sehemu.

Jibu

\(\dfrac{∂f}{∂x}=8x+2y+3\)

\(\dfrac{∂f}{∂y}=2x−2y−2\)

Wazo la kukumbuka wakati wa kuhesabu derivatives ya sehemu ni kutibu vigezo vyote vya kujitegemea, isipokuwa kutofautiana kwa heshima ambayo sisi ni kutofautisha, kama mara kwa mara. Kisha kuendelea kutofautisha kama na kazi ya variable moja. Kuona kwa nini hii ni kweli, kwanza kurekebisha\(y\) na kufafanua\(g(x)=f(x,y)\) kama kazi ya\(x\). Kisha

\[\begin{align*} g′(x) &=\lim_{h→0}\dfrac{g(x+h)−g(x)}{h} \\[6pt] &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\[6pt] &=\dfrac{∂f}{∂x}. \end{align*}\]

Vile vile ni kweli kwa kuhesabu derivative sehemu ya kuhusiana\(f\) na\(y\). Wakati huu, kurekebisha\(x\) na kufafanua\(h(y)=f(x,y)\) kama kazi ya\(y\). Kisha

\[\begin{align*} h′(x) &=\lim_{k→0}\dfrac{h(x+k)−h(x)}{k} \\[6pt] &=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k} \\[6pt] &=\dfrac{∂f}{∂y}. \end{align*}\]

Sheria zote za kutofautisha zinatumika.

Mfano\(\PageIndex{2}\): Calculating Partial Derivatives

Tumia\(∂f/∂x\) na\(∂f/∂y\) kwa kazi zifuatazo kwa kushikilia tofauti ya kutofautiana mara kwa mara kisha kutofautisha:

1. \(f(x,y)=x^2−3xy+2y^2−4x+5y−12\)
2. \(g(x,y)=\sin(x^2y−2x+4)\)

Suluhisho:

a Ili kuhesabu\(∂f/∂x\), kutibu variable\(y\) kama mara kwa mara. Kisha kutofautisha\(f(x,y)\) kwa heshima ya\(x\) kutumia jumla, tofauti, na sheria za nguvu:

\[\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}\]

Vipengee vya maneno ya tatu, ya tano, na ya sita yote ni sifuri kwa sababu hayana variable\(x\), hivyo hutendewa kama maneno ya mara kwa mara. Derivative ya muda wa pili ni sawa na mgawo wa\(x\), ambayo ni\(−3y\). Kuhesabu\(∂f/∂y\):

\[\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \nonumber \]

Hizi ni majibu sawa kupatikana katika Mfano\(\PageIndex{1}\).

b Ili kuhesabu\(∂g/∂x,\) kutibu y variable kama mara kwa mara. Kisha kutofautisha\(g(x,y)\) kwa heshima ya\(x\) kutumia utawala wa mnyororo na utawala wa nguvu:

\[\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}\]

Kuhesabu\(∂g/∂y,\) kutibu variable\(x\) kama mara kwa mara. Kisha kutofautisha\(g(x,y)\) kwa heshima ya\(y\) kutumia utawala wa mnyororo na utawala wa nguvu:

\[ \begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \nonumber \]

Zoezi\(\PageIndex{2}\)

Tumia\(∂f/∂x\) na\(∂f/∂y\) kwa kazi

\[f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber \]

kwa kufanya variable kinyume mara kwa mara, kisha kutofautisha.

Kidokezo

Tumia Equations\ ref {pd1} na\ ref {pd1} kutoka ufafanuzi wa derivatives sehemu.

Jibu

\(\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)\)

\(\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)\)

Tunawezaje kutafsiri derivatives hizi za sehemu? Kumbuka kwamba grafu ya kazi ya vigezo viwili ni uso ndani\(R^3\). Ikiwa tunaondoa kikomo kutoka kwa ufafanuzi wa derivative ya sehemu kwa heshima\(x\), tofauti ya quotient inabakia:

\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]

Hii inafanana na tofauti ya quotient kwa derivative ya kazi ya variable moja, ila kwa uwepo wa\(y\) kutofautiana. Kielelezo\(\PageIndex{1}\) unaeleza uso ilivyoelezwa na kazi holela\(z=f(x,y).\)

Kielelezo\(\PageIndex{1}\): Secant line kupita kwa njia ya pointi\((x,y,f(x,y))\) na\((x+h,y,f(x+h,y)).\)

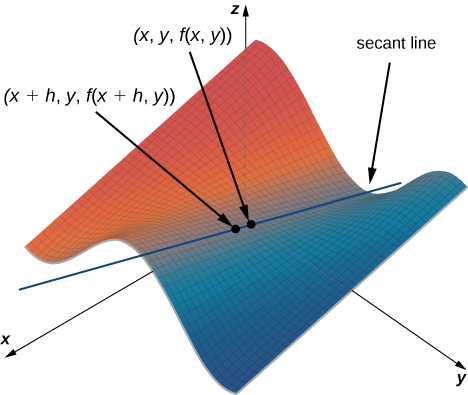
Katika Kielelezo\(\PageIndex{1}\), thamani ya\(h\) ni chanya. Ikiwa sisi grafu\(f(x,y)\) na\(f(x+h,y)\) kwa hatua ya kiholela,\((x,y),\) basi mteremko wa mstari wa salama unaopita kupitia pointi hizi mbili hutolewa na

\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]

Mstari huu ni sawa na\(x\) -axis. Kwa hiyo, mteremko wa mstari wa secant unawakilisha kiwango cha wastani cha mabadiliko ya kazi\(f\) tunaposafiri sambamba na\(x\) -axis. Kama\(h\) inakaribia sifuri, mteremko wa mstari wa salama unakaribia mteremko wa mstari wa tangent.

Ikiwa tunachagua kubadili\(y\) badala ya\(x\) thamani sawa ya ziada\(h\), basi mstari wa secant ni sawa na\(y\) -axis na hivyo ni mstari wa tangent. Kwa hiyo,\(∂f/∂x\) inawakilisha mteremko wa mstari wa tangent unaopitia hatua\((x,y,f(x,y))\) inayofanana na\(x\) -axis na\(∂f/∂y\) inawakilisha mteremko wa mstari wa tangent unaopitia hatua\((x,y,f(x,y))\) inayofanana na\(y\) -axis. Ikiwa tunataka kupata mteremko wa mstari wa tangent unaopitia hatua sawa katika mwelekeo mwingine wowote, basi tunahitaji kile kinachoitwa derivatives directional.

Sasa tunarudi kwenye wazo la ramani za contour, ambazo tumeanzisha katika Kazi za Vigezo kadhaa. Tunaweza kutumia ramani contour kukadiria derivatives sehemu ya kazi\(g(x,y)\).

Mfano\(\PageIndex{3}\): Partial Derivatives from a Contour Map

Tumia ramani ya contour ili kukadiria\(∂g/∂x\)\((\sqrt{5},0)\) kwa hatua ya kazi

\[g(x,y)=\sqrt{9−x^2−y^2}. \nonumber \]

Suluhisho

Kielelezo\(\PageIndex{2}\) inawakilisha ramani contour kwa ajili ya kazi\(g(x,y)\).

Kielelezo\(\PageIndex{2}\): Ramani ya contour kwa kazi\(g(x,y)=\sqrt{9−x^2−y^2}\), kutumia\(c=0,1,2,\) na\(3 (c=3\) inafanana na asili).

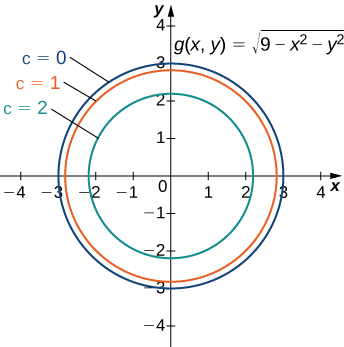
Mzunguko wa ndani kwenye ramani ya contour unafanana\(c=2\) na na mduara unaofuata unafanana na\(c=1\). Mduara wa kwanza unatolewa na equation\(2=\sqrt{9−x^2−y^2}\); mduara wa pili hutolewa na equation\(1=\sqrt{9−x^2−y^2}\). equation kwanza simplifies kwa\(x^2+y^2=5\) na equation pili simplifies\(x^2+y^2=8.\) kwa\(x\) -intercept ya mduara wa kwanza ni\((\sqrt{5},0)\) na\(x\) -intercept ya mduara wa pili ni\((2\sqrt{2},0)\). Tunaweza kukadiria thamani ya\(∂g/∂x\) tathmini kwa uhakika kwa\((\sqrt{5},0)\) kutumia formula ya mteremko:

\[ \begin{align*} \left.\dfrac{∂g}{∂x}\right|_{(x,y) = (\sqrt{5},0)} &≈ \dfrac{g(\sqrt{5},0)−g(2\sqrt{2},0)}{\sqrt{5}−2\sqrt{2}} \\ &= \dfrac{2−1}{\sqrt{5}−2\sqrt{2}} \\ &=\dfrac{1}{\sqrt{5}−2\sqrt{2}} ≈−1.688. \end{align*}\]

Ili kuhesabu thamani halisi ya\(∂g/∂x\) tathmini wakati huo\((\sqrt{5},0)\), tunaanza kwa kutafuta\(∂g/∂x\) kutumia utawala wa mnyororo. Kwanza, tunaandika upya kazi kama

\[g(x,y)=\sqrt{9−x^2−y^2}=(9−x^2−y^2)^{1/2} \nonumber \]

na kisha kutofautisha kwa heshima na\(x\) wakati kufanya\(y\) mara kwa mara:

\[ \begin{align*} \dfrac{∂g}{∂x} &=\dfrac{1}{2}(9−x^2−y^2)^{−1/2}(−2x) \\[4pt] &=−\dfrac{x}{\sqrt{9−x^2−y^2}}. \end{align*}\]

Kisha, tunatathmini maneno haya kwa kutumia\(x=\sqrt{5}\) na\(y=0\):

\ [kuanza {align*}\ dfrac {g} {x} _ {x, y) = (\ sqrt {5} ,0)} &=\ dfrac {\ sqrt {5}} {\ sqrt {9} (\ sqrt {5}) ^2 (0) ^2}}\ [4pt]
&=\ drac {\ sqrt {5} {\ sqrt {4}}\ [4pt]
&=\ drac {\ sqrt {5}} {2} ≈ 18-1.118. \ mwisho {align*}\ nonumber\]

Makadirio ya derivative ya sehemu inalingana na mteremko wa mstari wa salama unaopita kupitia pointi\((\sqrt{5},0,g(\sqrt{5},0))\) na\((2\sqrt{2},0,g(2\sqrt{2},0))\). Inawakilisha makadirio ya mteremko wa mstari tangent kwa uso kupitia hatua\((\sqrt{5},0,g(\sqrt{5},0)),\) ambayo ni sambamba na\(x\) -axis.

Zoezi\(\PageIndex{3}\)

Tumia ramani ya contour ili kukadiria\((0,\sqrt{2})\) kwa\(∂f/∂y\) hatua ya kazi

\[ f(x,y)=x^2−y^2.\nonumber \]

Linganisha hili na jibu halisi.

Kidokezo

Unda ramani ya contour kwa\(f\) kutumia maadili ya\(c\) kutoka\(−3\) kwa\(3\). Ni ipi kati ya curves hizi hupita kupitia hatua\((0,\sqrt{2})?\)

Jibu

Kwa kutumia curves sambamba\(c=−2\) na\(c=−3,\) sisi kupata

\ [\ kuanza {align*}\ kushoto. \ dfrac {f} {y}\ haki|_ {(x, y) = (0,\ sqrt {2})} &≈\ dfrac {f (0,\ sqrt {3}) -f (0,\ sqrt {2})} {\ sqrt {3}}\ [4pt]
&=\ drac {3—2} {\ sqrt {3}}} {\ sqrt {2}}}\ drac {\ sqrt {3} +\ sqrt {2}} {\ sqrt {3} +\ sqrt {2}}\ [4pt]
&=\ sqrt {3}}\ sqrt {2} ≈ 3.146. \ mwisho {align*}\]

Jibu halisi ni

\[ \left. \dfrac{∂f}{∂y} \right|_{(x,y)=(0,\sqrt{2})}=(−2y|_{(x,y)=(0,\sqrt{2})}=−2\sqrt{2}≈−2.828. \nonumber \]

Kazi za Vigezo Zaidi ya mbili

Tuseme tuna kazi ya vigezo tatu, kama vile\(w=f(x,y,z).\) Tunaweza kuhesabu derivatives sehemu ya kuhusiana\(w\) na yoyote ya vigezo huru, tu kama upanuzi wa ufafanuzi kwa derivatives sehemu ya kazi ya vigezo mbili.

Ufafanuzi: Derivativ

Hebu\(f(x,y,z)\) kuwa kazi ya vigezo tatu. Kisha, derivative sehemu ya kuhusiana\(f\) na\(x\), imeandikwa kama\(∂f/∂x,\) au\(f_x,\) ni defined kuwa

\[\dfrac{∂f}{∂x}=f_x(x,y,z)=\lim_{h→0}\dfrac{f(x+h,y,z)−f(x,y,z)}{h}. \label{PD2a} \]

derivative sehemu ya kuhusiana\(f\) na\(y\), imeandikwa kama\(∂f/∂y\), au\(f_y\), hufafanuliwa kuwa

\[\dfrac{∂f}{∂y}=f_y(x,y,z)=\lim_{k→0}\dfrac{f(x,y+k,z)−f(x,y,z)}{k.} \label{PD2b} \]

derivative sehemu ya kuhusiana\(f\) na\(z\), imeandikwa kama\(∂f/∂z\), au\(f_z\), hufafanuliwa kuwa

\[\dfrac{∂f}{∂z}=f_z(x,y,z)=\lim_{m→0}\dfrac{f(x,y,z+m)−f(x,y,z)}{m}. \label{PD2c} \]

Tunaweza mahesabu derivative sehemu ya kazi ya vigezo tatu kwa kutumia wazo moja sisi kutumika kwa ajili ya kazi ya vigezo mbili. Kwa mfano, kama tuna kazi\(f\) ya\(x,y\), na\(z\), na tunataka kufanya mahesabu\(∂f/∂x\), basi sisi kutibu wengine wawili vigezo huru kama kama ni constants, kisha kutofautisha kwa heshima na\(x\).

Mfano\(\PageIndex{4}\): Calculating Partial Derivatives for a Function of Three Variables

Tumia ufafanuzi wa kikomo wa derivatives ya sehemu ili uhesabu\(∂f/∂x\) kwa kazi

\[ f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z. \nonumber \]

Kisha, tafuta\(∂f/∂y\) na\(∂f/∂z\) kwa kuweka vigezo vingine viwili mara kwa mara na kutofautisha ipasavyo.

Suluhisho:

Sisi kwanza mahesabu\(∂f/∂x\) kwa kutumia Equation\ ref {PD2A}, basi sisi mahesabu mengine mawili derivatives sehemu kwa kufanya iliyobaki vigezo mara kwa mara. Ili kutumia equation kupata\(∂f/∂x\), sisi kwanza haja ya kuhesabu\(f(x+h,y,z):\)

\ [kuanza {align*} f (x+h, y, z) &= (x+h) ^2,13 (x+h) y+2y ^ 2y-4 (x+h) z+5yz ^ 2,112 (x+h) +4y-3z\\ [4pt]
&x ^ 2+2xh+h ^ 2,13xy-1 3xh+2y ^ 2—4xz-4hz+5yz ^ 2,112x-12h+4y-3z\ mwisho {align*}\ nonumber\]

na kukumbuka kwamba\(f(x,y,z)=x^2−3xy+2y^2−4zx+5yz^2−12x+4y−3z.\) Next, sisi badala ya maneno haya mawili katika equation:

\ [kuanza {align*}\ dfrac {f} {x} &=\ lim_ {h → 0}\ kushoto [\ dfrac {x ^ 2+2xh+h ^ 2,13xy-3hy+2y ^ 2,14hz-4hz+5yz ^ 2,1xy-12h+4Y-3h+2y ^ 2,12y ^ 2,12y ^ 2,121-2Y^2y 4xz+5yz ^ 2,112x+4y-3z} {h}\ haki]\\ [4pt]
&=\ lim_ {h → 0}\ kushoto [\ dfrac {2xh+h ^ 2,13h-4hz-12h} {h}\ haki]\\ [4pt]
&=\ lim_ {h → 0}\ kushoto [\ dfrac {h (2x+h-3y-4z-12 )} {h}\ haki]\\ [4pt]
&=\ lim_ {h→ 0} (2x+h-3y-4z-12)\\ [4pt]
&=2x-3y-4z-12. \ mwisho {align*}\ nonumber\]

Kisha sisi kupata\(∂f/∂y\) kwa kufanya\(x\) na\(z\) mara kwa mara. Kwa hiyo, neno lolote ambalo halijumuishi kutofautiana\(y\) ni mara kwa mara, na derivative yake ni sifuri. Tunaweza kutumia jumla, tofauti, na sheria za nguvu kwa kazi za kutofautiana moja:

\ [kuanza {align*} &\ dfrac {} {y}\ kushoto [x ^ 2,13xy+2y ^ 2,14xz+5yz ^ 2,112x+4y-3z\ haki]\\ [4pt]
&=\ dfrac {} {y} {y} {y} [3xy] +\ dfrac {} {y} [2y ^ 2] -\ dfrac {} {y} [4xz] +\ dfrac {} {y} [5yz ^ 2] -\ dfrac {} {y} [12x] +\ dfrac {} {y} [4y] -\ dfrac {} z} [3z]\\ [4pt]
&=0,13x+4y-0+5z^2,10+4,10 \\ [4pt]
&=-3x+4y+5z ^ 2+4. \ mwisho {align*}\]

Ili kuhesabu\(∂f/∂z,\) tunashikilia\(x\) na\(y\) mara kwa mara na kutumia jumla, tofauti, na sheria za nguvu kwa kazi za kutofautiana moja:

\ [kuanza {align*} &\ dfrac {} {z} [x^2,13xy+2y ^ 2,14xz+5yz ^ 2,1x+4y-3z]\\ [4pt]
&=\ dfrac {} {z} {z} {z} [3xy] +\ dfrafc {z} {z} [2y ^ 2] -\ dfrac {} {z} [4xz] +\ dfrac {} {z} [5yz ^ 2] -\ dfrac {} {z} [12x] +\ dfrac {} {z} {z} [3z]\\ [4pt]
&=0,1-0+0,14x+10yz-0+0,13\\ [4pt]
&=-4x+10yz-3\ mwisho {align*}\]

Zoezi\(\PageIndex{4}\)

Tumia ufafanuzi wa kikomo wa derivatives ya sehemu ili uhesabu\(∂f/∂x\) kwa kazi

\[f(x,y,z)=2x^2−4x^2y+2y^2+5xz^2−6x+3z−8.\nonumber \]

Kisha kupata\(∂f/∂y\) na\(∂f/∂z\) kwa kuweka vigezo vingine viwili mara kwa mara na kutofautisha ipasavyo.

Kidokezo

Tumia mkakati katika mfano uliotangulia.

Jibu

\(\dfrac{∂f}{∂x}=4x−8xy+5z^2−6,\dfrac{∂f}{∂y}=−4x^2+4y,\dfrac{∂f}{∂z}=10xz+3\)

Mfano\(\PageIndex{5}\): Calculating Partial Derivatives for a Function of Three Variables

Tumia derivatives tatu za sehemu ya kazi zifuatazo.

1. \(f(x,y,z)=x^2y−4xz+y^2x−3yz\)
2. \(g(x,y,z)=\sin(x^2y−z)+\cos(x^2−yz)\)

Suluhisho

Katika kila kesi, kutibu vigezo vyote kama constants isipokuwa moja ambaye sehemu derivative wewe ni kuhesabu.

a.

\ [kuanza {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ kushoto [\ dfrac {x ^ 2y-4xz+y ^ 2} {x-3yz}\ haki]\\ [6pt]
&=\ dfrac {\ dfrac {} {x} (x ^ 2y-4x-4xx z+y ^ 2) (x-3yz) - (x^2y-4xz+y ^ 2)\ dfrac {} {x} (x-3yz)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {(2xy-4z) (x-3yz) - (x^2y—4z) y ^ 2) (1)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {2x^2y-6xy ^ 2z-4xy+12yz^2y+2y+4xz—y ^ 2} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {x ^ 2y-6xy ^ 2z-12yz ^ 2+4xy y ^ 2} {(x—3yz) {(x—3yz) ^2} {(x—3yz) {(x—3yz) ^2+4xy y ^ 2} {(x—3yz) yz) ^2}\ mwisho {align*}\]

\ [kuanza {align*}\ dfrac {f} {y} &=\ dfrac {} {y}\ kushoto [\ dfrac {x^2y-4xz+y ^ 2} {x-3yz}\ haki]\\ [6pt]
&=\ dfrac {\ dfrac {} {y} (x ^ 2y-4x-4xx z+y ^ 2) (x-3yz) - (x^2y-4xz+y ^ 2)\ dfrac {} {y} (x-3yz)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {(x ^ 2+2y) (x-3yz) - (x ^ 2y—4xz+z+y ^ 2) (-3z)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {x ^ 3x^2yz+2xy-6y ^ 2z+3x^2yz—12xz ^ 2+3y ^ 2z} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {x ^ 3+2xy-3y ^ 2z—12xz ^ 2} {(x-3yz) ^2}\ mwisho {align*}\]

\ [kuanza {align*}\ dfrac {f} {z} &=\ dfrac {} {z}\ kushoto [\ dfrac {x^2y-4xz+y ^ 2} {x-3yz}\ haki]\\ [6pt]
&=\ dfrac {\ dfrac {} {z} (x^2y-4x-4xx z+y ^ 2) (x-3yz) - (x^2y-4xz+y ^ 2)\ dfrac {} {z} (x-3yz)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {(-4x) (x-3yz) - (x^2y-4xz+y ^ 2) (-3y)} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {-4x^2+12xyz+3x ^ 2y ^ 2,112xyz+3y ^ 3} {(x-3yz) ^2}\\ [6pt]
&=\ dfrac {-4x^2+3x ^ 2y ^2+3y ^ 3} {(x-3yz) ^2}\ mwisho {urekebisho*}\]

b.

\ [kuanza {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ kushoto [\ dhambi (x ^ 2y-z) +\ cos (x^2,1yz)\ haki]\\ [6pt]
& =(\ cos (x ^ 2y-z))\ dfrac {} {x} (x ^ 2y-z)\ dfrac {} {x} (x ^ 2y-z)\\ 2y-z) - (\ dhambi (x^2,1yz))\ dfrac {} {x} (x^2,1yz)\\ [6pt]
&=2y\ cos (x^2y-z) -2x\ dhambi (x^2,1yz)\ mwisho {align*}\]

\ [kuanza {align*}\ dfrac {f} {y} &=\ dfrac {} {y} [\ dhambi (x^2y-z) +\ cos (x^2y-yz)]\\ [6pt]
& =(\ cos (x ^ 2y-z))\ dfrac {} {y} (x ^ 2y-z)) - (\ dhambi (x^2,1yz))\ dfrac {} {y} (x ^ 2,1yz)\\ [6pt]
&=x ^ 2\ cos (x ^ 2y-z) +z\ dhambi (x^2,1yz)\ mwisho {align*}\]

\ [kuanza {align*}\ dfrac {f} {z} &=\ dfrac {} {z} [\ dhambi (x^2y-z) +\ cos (x^2y-yz)]\\ [6pt]
& =(\ cos (x ^ 2y-z))\ dfrac {} {z} (x ^ 2y-z)) - (\ dhambi (x^2,1yz))\ dfrac {} {z} (x ^ 2,1yz)\\ [6pt]
&=\cos (x ^ 2y-z) +y\ dhambi (x^2,1yz)\ mwisho {align*}\ nonumber\]

Zoezi\(\PageIndex{5}\)

Tumia\(∂f/∂x, ∂f/∂y,\) na\(∂f/∂z\) kwa kazi

\[f(x,y,z)=\sec(x^2y)−\tan(x^3yz^2). \nonumber \]

Kidokezo

Tumia mkakati katika mfano uliotangulia.

Jibu

\(\dfrac{∂f}{∂x}=2xy\sec(x^2y)\tan(x^2y)−3x^2yz^2\sec^2(x^3yz^2)\)

\(\dfrac{∂f}{∂y}=x^2\sec(x^2y)\tan(x^2y)−x^3z^2\sec^2(x^3yz^2)\)

\(\dfrac{∂f}{∂z}=−2x^3yz\sec^2(x^3yz^2)\)

Derivatives sehemu ya juu

Fikiria kazi

\[f(x,y)=2x^3−4xy^2+5y^3−6xy+5x−4y+12. \nonumber \]

Derivatives yake sehemu ni

\[\dfrac{∂f}{∂x}=6x^2−4y^2−6y+5 \nonumber \]

na

\[\dfrac{∂f}{∂y}=−8xy+15y^2−6x−4. \nonumber \]

Kila moja ya derivatives hizi sehemu ni kazi ya vigezo mbili, hivyo tunaweza kuhesabu derivatives sehemu ya kazi hizi. Kama ilivyo na derivatives ya kazi moja-variable, tunaweza kuwaita derivatives hizi za pili, derivatives ya tatu, na kadhalika. Kwa ujumla, hujulikana kama derivatives ya sehemu ya juu. Kuna aina nne za pili za sehemu ya pili kwa kazi yoyote (ikiwa ni pamoja na yote yapo):

\ [kuanza {align*}\ dfrac {^2f} {x ^ 2} &=\ dfrac {} {x}\ kushoto [\ dfrac {f} {x}\ haki]\
\ [4pt]\ dfrac {^2f} {yx} {y}\ kushoto [\ dfrac {f} {x}\ haki]\ [4pt]
\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ kushoto [\ dfrac {f} {y}\ haki]\\ [4pt]
\ dfrac {^2f} {y ^ 2} &=\ dfrac {} {y}\ kushoto [\ dfrac {f} {y}\ haki]. \ mwisho {align*}\]

Notation mbadala kwa kila mmoja ni\(f_{xx},f_{xy},f_{yx},\) na\(f_{yy}\), kwa mtiririko huo. Higur-ili sehemu derivatives mahesabu kwa heshima na vigezo mbalimbali, kama vile\(f_{xy}\) na\(f_{yx}\), ni kawaida huitwa mchanganyiko sehemu derivatives.

Mfano\(\PageIndex{6}\): Calculating Second Partial Derivatives

Tumia derivatives zote nne za sehemu ya pili kwa kazi

\[f(x,y)=xe^{−3y}+\sin(2x−5y).\label{Ex6e1} \]

Suluhisho:

Ili kuhesabu\(\dfrac{∂^2f}{∂x^2}\) na\(\dfrac{∂^2f}{∂y∂x}\), sisi kwanza tunahesabu\(∂f/∂x\):

\[\dfrac{∂f}{∂x}=e^{−3y}+2\cos(2x−5y). \label{Ex6e2} \]

Ili kuhesabu\(\dfrac{∂^2f}{∂x^2}\), kutofautisha\(∂f/∂x\) (Equation\ ref {ex6E2}) kwa heshima na\(x\):

\ [kuanza {align*}\ dfrac {^2f} {x ^ 2} &=\ dfrac {} {x}\ kushoto [\ dfrac {f} {x}\ haki]\\ [6pt]
&=\ dfrac {} {x} [e^ {-3y} +2\ cos (2x-5y)]\\ [6pt]
&=—4\ dhambi (2x-5y). \ mwisho {align*}\ nonumber\]

Ili kuhesabu\(\dfrac{∂^2f}{∂y∂x}\), kutofautisha\(∂f/∂x\) (Equation\ ref {ex6E2}) kwa heshima na\(y\):

\ [kuanza {align*}\ dfrac {^2f} {y\, x} &=\ dfrac {} {y}\ kushoto [\ dfrac {f} {x}\ haki]\\ [6pt]
&=\ dfrac {} {y} [e^ {-3y} +2\ cos (2x-5y)]\\ [6pt]
&=-3e^ {-3y} +10\ dhambi (2x-5y). \ mwisho {align*}\ nonumber\]

Ili kuhesabu\(\dfrac{∂^2f}{∂x∂y}\) na\(\dfrac{∂^2f}{∂y^2}\), kwanza uhesabu\(∂f/∂y\):

\[\dfrac{∂f}{∂y}=−3xe^{−3y}−5\cos(2x−5y). \label{Ex6e5} \]

Ili kuhesabu\(\dfrac{∂^2f}{∂x∂y}\), kutofautisha\(∂f/∂y\) (Equation\ ref {ex6E5}) kwa heshima na\(x\):

\ [kuanza {align*}\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ kushoto [\ dfrac {f} {y}\ haki]\\ [6pt]
&=\ dfrac {} {x} [-3xe^ {-3y} -5\ cos (2x-5y)]\\ [6pt]
&=-3e^ {-3y} +10\ dhambi (2x-5y). \ mwisho {align*}\ nonumber\]

Ili kuhesabu\(\dfrac{∂^2f}{∂y^2}\), kutofautisha\(∂f/∂y\) (Equation\ ref {ex6E5}) kwa heshima na\(y\):

\ [kuanza {align*}\ dfrac {^2f} {y ^2} &=\ dfrac {} {y}\ kushoto [\ dfrac {f} {y}\ haki]\\ [6pt]
&=\ dfrac {y} {y} {-3y} -5\ cos (2x-5y)]\\ [6pt]
&=9xe^ {-3y} -25\ dhambi (2x-5y). \ mwisho {align*}\ nonumber\]

Zoezi\(\PageIndex{6}\)

Tumia derivatives zote nne za sehemu ya pili kwa kazi

\[f(x,y)=\sin(3x−2y)+\cos(x+4y).\nonumber \]

Kidokezo

Fuata hatua sawa na katika mfano uliopita.

Jibu

\(\dfrac{∂^2f}{∂x^2}=−9\sin(3x−2y)−\cos(x+4y)\)

\(\dfrac{∂^2f}{∂y∂x}=6\sin(3x−2y)−4\cos(x+4y)\)

\(\dfrac{∂^2f}{∂x∂y}=6\sin(3x−2y)−4\cos(x+4y)\)

\(\dfrac{∂^2f}{∂y^2}=−4\sin(3x−2y)−16\cos(x+4y)\)

Katika hatua hii tunapaswa kutambua kwamba, katika wote Mfano\(\PageIndex{6}\) na checkpoint, ilikuwa kweli kwamba\(\dfrac{∂^2f}{∂y∂x}=\dfrac{∂^2f}{∂x∂y}\). Chini ya hali fulani, hii ni kweli daima. Kwa kweli, ni matokeo ya moja kwa moja ya theorem ifuatayo.

Usawa wa Derivatives ya sehemu ya mchanganyiko (Theorem ya Clairaut)

Tuseme kwamba\(f(x,y)\) inafafanuliwa kwenye diski\(D\) iliyo wazi ambayo ina uhakika\((a,b)\). Ikiwa kazi\(f_{xy}\) na\(f_{yx}\) zinaendelea\(D\), basi\(f_{xy}=f_{yx}\).

Theorem ya Clairaut inathibitisha kwamba kwa muda mrefu kama mchanganyiko wa derivatives ya pili ya utaratibu unaendelea, utaratibu ambao tunachagua kutofautisha kazi (yaani, ambayo kutofautiana huenda kwanza, kisha pili, na kadhalika) haijalishi. Inaweza kupanuliwa kwa derivatives ya juu-ili pia. Ushahidi wa theorem ya Clairaut inaweza kupatikana katika vitabu vya juu vya calculus.

Mbili nyingine ya pili ili sehemu derivatives inaweza kuwa mahesabu kwa kazi\(f(x,y).\) yoyote. sehemu derivative\(f_{xx}\) ni sawa\(f_x\) na derivative sehemu ya kuhusiana na\(x\), na\(f_{yy}\) ni sawa na derivative sehemu ya kuhusiana\(f_y\) na\(y\).

Mlinganyo wa kutofautiana kwa sehemu

Hapo awali, tulijifunza equations tofauti ambayo kazi haijulikani ilikuwa na tofauti moja ya kujitegemea. Equation ya tofauti ya sehemu ni equation ambayo inahusisha kazi isiyojulikana ya kutofautiana zaidi ya moja ya kujitegemea na moja au zaidi ya derivatives yake ya sehemu. Mifano ya equations tofauti ya sehemu ni

\[\underset{\text{heat equation in two dimensions}}{u_t=c^2(u_{xx}+u_{yy})} \nonumber \]

\[\underset{\text{wave equation in two dimensions}}{u_{tt}=c^2(u_{xx}+u_{yy})} \nonumber \]

\[\underset{\text{Laplace’s equation in two dimensions}} {u_{xx}+u_{yy}=0} \nonumber \]

Katika usawa wa joto na wimbi, kazi isiyojulikana\(u\) ina vigezo vitatu vya kujitegemea:\(t\),\(x\),\(y\) na\(c\) ni mara kwa mara ya kiholela. Vigezo vya kujitegemea\(x\) na\(y\) vinachukuliwa kuwa vigezo vya anga, na variable\(t\) inawakilisha wakati. Katika equation Laplace ya, kazi haijulikani\(u\) ina vigezo mbili huru\(x\) na\(y\).

Mfano\(\PageIndex{7}\): A Solution to the Wave Equation

Thibitisha kwamba

\[u(x,y,t)=5\sin(3πx)\sin(4πy)\cos(10πt) \nonumber \]

ni suluhisho la equation ya wimbi

\[u_{tt}=4(u_{xx}+u_{yy}). \label{Ex7Eq2} \]

Suluhisho

Kwanza, tunahesabu\(u_{tt},u_{xx},\) na\(u_{yy}:\)

\ [kuanza {align*} u_ {tt} (x, y, t) &=\ dfrac {} {t}\ kushoto [\ dfrac {u} {t}\ haki]\\ [6pt]
&=\ dfrac {} {t} [5\ dhambi (3πx)\ dhambi (4πy) (-10π\ dhambi (10π)\ πt)]\\ [6pt]
&=\ dfrac {} {t}\ kushoto [-50π\ dhambi (3πx)\ dhambi (4πy)\ dhambi (10πt)\ haki]\\ [6pt]
&=-500π^2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt)\ mwisho {align*}\]

\ [kuanza {align*} u_ {xx} (x, y, t) &=\ dfrac {} {x}\ kushoto [\ dfrac {u} {x}\ haki]\\ [6pt]
&=\ dfrac {} {x}\ kushoto [15π\ cos (3πx)\ dhambi (4πy)\ cos (10πy)\ t)\ haki]\\ [6pt]
&=-45π^2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt)\ mwisho {align*}\]

\ [kuanza {align*} u_ {yy} (x, y, t) &=\ dfrac {} {y}\ kushoto [\ dfrac {u} {y}\ haki]\\ [6pt]
&=\ dfrac {} {y}\ kushoto [5\ dhambi (3πx) (4π\ cos (4πy)) cos\ (10πt)\ haki]\\ [6pt]
&=\ dfrac {} {y}\ kushoto [20π\ dhambi (3πx)\ cos (4πy)\ cos (10πt)\ haki]\\ [6pt]
&=-80π^2\ dhambi (3πx)\ dhambi (4πy)\ cos ( 10πt). \ mwisho {align*}\ nonumber\]

Kisha, sisi badala ya kila moja ya haya katika upande wa kulia wa Equation\ ref {Ex7Eq2} na kurahisisha:

\ [kuanza {align*} 4 (u_ {xx} +u_ {yy}) &=4 (-45π^2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt) +-80π^2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt))\\ [6pt]
&=4 (-125^ππππ2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt))\\ [6pt]
&=-500π^2\ dhambi (3πx)\ dhambi (4πy)\ cos (10πt)\\ [6pt]
&=u_ {tt}. \ mwisho {align*}\]

Hii inathibitisha ufumbuzi.

Zoezi\(\PageIndex{7}\): A Solution to the Heat Equation

Thibitisha kwamba

\[u(x,y,t)=2\sin \left(\dfrac{x}{3} \right)\sin\left(\dfrac{y}{4} \right)e^{−25t/16} \nonumber \]

ni suluhisho la equation ya joto

\[u_t=9(u_{xx}+u_{yy}). \nonumber \]

Kidokezo

Tumia derivatives ya sehemu na mbadala katika upande wa kulia.

Jibu

TBA

Kwa kuwa suluhisho la usawa wa joto la pande mbili ni kazi ya vigezo vitatu, si rahisi kuunda uwakilishi wa kuona wa suluhisho. Tunaweza kugawa suluhisho kwa maadili yaliyowekwa\(t,\) ambayo yanafanana na picha za mgawanyo wa joto wakati uliowekwa. Picha hizi zinaonyesha jinsi joto linavyosambazwa juu ya uso wa pande mbili kadiri muda unavyoendelea. Grafu ya ufumbuzi uliotangulia wakati\(t=0\) unaonekana kwenye Kielelezo\(\PageIndex{3}\). Kama muda unaendelea, extremes ngazi nje, inakaribia sifuri kama\(t\) mbinu infinity.

Kielelezo\(\PageIndex{3}\)

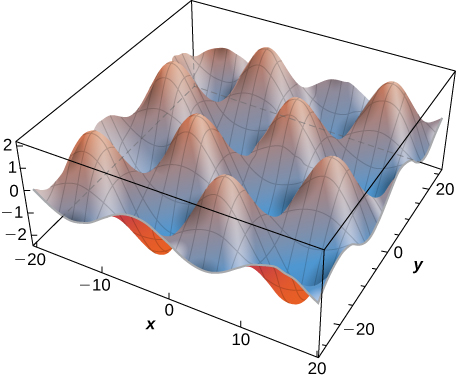
Ikiwa tunazingatia usawa wa joto kwa mwelekeo mmoja, basi inawezekana kufuta suluhisho kwa muda. Equation ya joto katika mwelekeo mmoja inakuwa

\[u_t=c^2u_{xx}, \nonumber \]

ambapo\(c^2\) inawakilisha diffusivity mafuta ya nyenzo katika swali. Suluhisho la equation hii tofauti inaweza kuandikwa kwa fomu

\[u_m(x,t)=e^{−π^2m^2c^2t}\sin(mπx) \nonumber \]

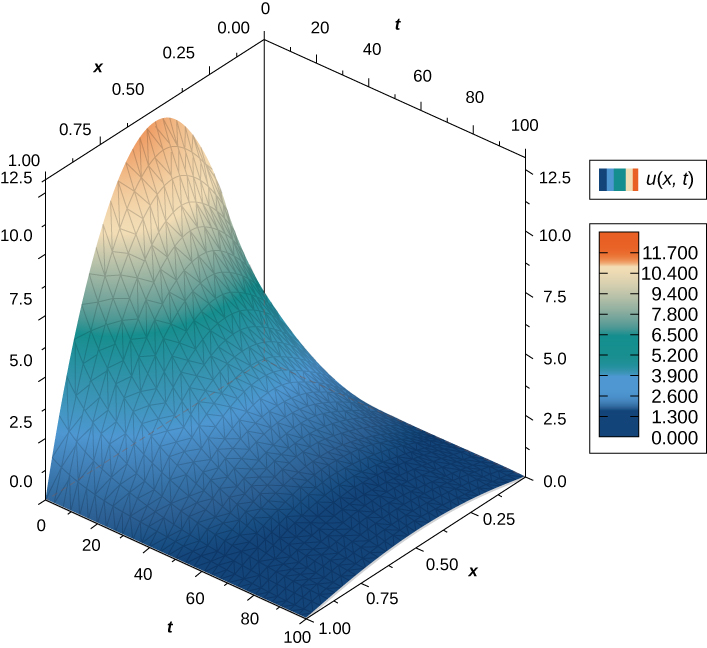
ambapo\(m\) ni integer yoyote chanya. Grafu ya ufumbuzi huu kwa kutumia\(m=1\) inaonekana kwenye Kielelezo\(\PageIndex{4}\), ambapo usambazaji wa joto la awali juu ya waya wa urefu\(1\) hutolewa na\(u(x,0)=\sin πx.\) Taarifa kwamba wakati unavyoendelea, waya huzima. Hii inaonekana kwa sababu, kutoka kushoto kwenda kulia, joto la juu (ambalo hutokea katikati ya waya) hupungua na hubadilisha rangi kutoka nyekundu hadi bluu.

Kielelezo\(\PageIndex{4}\): Grafu ya suluhisho la equation ya joto katika mwelekeo mmoja baada ya muda.

Bwana Kelvin na Umri wa Dunia

Wakati wa miaka ya 1800, wanasayansi wa uwanja mpya wa jiolojia walikuwa wanafikia hitimisho kwamba Dunia lazima iwe “mamilioni na mamilioni” ya umri wa miaka. Wakati huo huo, Charles Darwin alikuwa amechapisha makala yake juu ya mageuzi. Mtazamo wa Darwin ulikuwa kwamba mageuzi yalihitaji mamilioni ya miaka mingi kufanyika, na alifanya madai ya ujasiri kwamba mashamba ya chaki ya Weald, ambapo fossils muhimu zilipatikana, zilikuwa matokeo ya miaka\(300\) milioni ya mmomonyoko wa ardhi.

Kielelezo\(\PageIndex{5}\): (a) William Thomson (Bwana Kelvin), 1824-1907, alikuwa mwanafizikia wa Uingereza na mhandisi wa umeme; (b) Kelvin alitumia usawa wa usambazaji wa joto ili kukadiria umri wa Dunia (mikopo: mabadiliko ya kazi na NASA).

Wakati huo, mwanafizikia maarufu William Thomson (Bwana Kelvin) alitumia equation muhimu ya kutofautisha sehemu, inayojulikana kama equation ya utbredningen wa joto, ili kukadiria umri wa Dunia kwa kuamua muda gani itachukua Dunia kuwa baridi kutoka mwamba kuyeyuka hadi kile tulichokuwa nacho wakati huo. Hitimisho lake lilikuwa miaka mingi ya milioni 20 hadi 400, lakini uwezekano mkubwa kuhusu miaka milioni 50. Kwa miongo mingi, matangazo ya icon hii isiyoweza kukataliwa ya sayansi haikukaa vizuri na wanajiolojia au Darwin.

• Soma karatasi ya Kelvin juu ya kukadiria umri wa Dunia.

Kelvin alifanya mawazo ya busara kulingana na kile kilichojulikana wakati wake, lakini pia alifanya mawazo kadhaa ambayo yaligeuka kuwa mabaya. Dhana moja isiyo sahihi ilikuwa kwamba Dunia ni imara na kwamba baridi hiyo ilikuwa kupitia upitishaji tu, hivyo kuhalalisha matumizi ya equation ya utbredningen. Lakini hitilafu kubwa zaidi ilikuwa moja ya kusamehewa - upungufu wa ukweli kwamba Dunia ina elementi za mionzi ambazo zinaendelea kutoa joto chini ya vazi la Dunia. Ugunduzi wa radioactivity ulifika karibu na mwisho wa maisha ya Kelvin na alikubali kuwa hesabu yake ingebadilishwa.

Kelvin alitumia mfano rahisi wa mwelekeo mmoja uliotumiwa tu kwa shell ya nje ya Dunia, na ilitokana na umri kutoka kwenye grafu na gradient ya joto inayojulikana karibu na uso wa Dunia. Hebu tuangalie toleo sahihi zaidi la usawa wa usambazaji katika kuratibu za radial, ambazo zina fomu

\[\dfrac{∂T}{∂t}=K\left[\dfrac{∂^2T}{∂^2r}+\dfrac{2}{r}\dfrac{∂T}{∂r}\right] \label{kelvin1} \].

Hapa,\(T(r,t)\) ni joto kama kazi ya\(r\) (kupimwa kutoka katikati ya Dunia) na wakati\(t. K\) ni joto conductivity—kwa mwamba kuyeyuka, katika kesi hii. Njia ya kawaida ya kutatua usawa wa kutofautiana kwa sehemu hiyo ni kwa kujitenga kwa vigezo, ambapo tunaelezea suluhisho kama bidhaa za kazi zilizo na kila kutofautiana tofauti. Katika kesi hiyo, tunataka kuandika joto kama

\[T(r,t)=R(r)f(t). \nonumber \]

1. Badilisha fomu hii katika Equation\ ref {kelvin1} na, akibainisha kuwa\(f(t)\) ni mara kwa mara kwa heshima\((r)\) na umbali na\(R(r)\) ni mara kwa mara kwa heshima na wakati\((t)\), onyesha kwamba\[\dfrac{1}{f}\dfrac{∂f}{∂t}=\dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]. \nonumber \]
2. Equation hii inawakilisha mgawanyo wa vigezo tunataka. upande wa kushoto ni tu kazi ya\(t\) na upande wa kulia ni tu kazi ya\(r\), na lazima kuwa sawa kwa maadili yote ya\(r\) na\(t\). Kwa hiyo, wote wawili lazima wawe sawa na mara kwa mara. Hebu tupige simu hiyo mara kwa mara\(−λ^2\). (Urahisi wa uchaguzi huu unaonekana kwenye ubadilishaji.) Hivyo, tuna\[\dfrac{1}{f}\dfrac{∂f}{∂t}=−λ^2 \text{and} \dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]=−λ^2. \nonumber \]
3. Sasa, tunaweza kuthibitisha kwa njia ya kubadilisha moja kwa moja kwa kila equation kwamba ufumbuzi ni\(f(t)=Ae^{−λ^2t}\) na\(R(r)=B\left(\dfrac{\sin αr}{r}\right)+C\left(\dfrac{\cos αr}{r}\right)\), wapi\(α=λ/\sqrt{K}\). Kumbuka kwamba pia\(f(t)=Ae^{+λn^2t}\) ni suluhisho halali, hivyo tunaweza kuwa waliochaguliwa\(+λ^2\) kwa mara kwa mara yetu. Je, unaweza kuona kwa nini itakuwa halali kwa kesi hii kama ongezeko wakati?
4. Hebu sasa tufanye hali ya mipaka.
   1. Joto lazima liwe la mwisho katikati ya Dunia,\(r=0\). Ni ipi kati ya constants mbili\(C\),\(B\) au, lazima kwa hiyo kuwa sifuri kuweka\(R\) finite katika\(r=0\)? (Kumbuka kwamba\(\sin(αr)/r→α=\) kama\(r→0\), lakini\(\cos(αr)/r\) tabia tofauti sana.)
   2. Kelvin alisema kuwa wakati magma inakaribia uso wa Dunia, inakua haraka sana. Mtu anaweza kugusa uso ndani ya wiki za mtiririko. Kwa hiyo, uso ulifikia joto la wastani mapema sana na ulibaki karibu mara kwa mara kwenye joto la uso\(T_s\). Kwa unyenyekevu, hebu\(T=0\)\(r=R_E\) tuweke na tupate α kama kwamba hii ni joto huko kwa wakati wote\(t\). (Kelvin alichukua thamani kuwa\(300K≈80°F\). Tunaweza kuongeza hii\(300K\) mara kwa mara kwenye suluhisho letu baadaye.) Kwa hili kuwa kweli, hoja sine lazima sifuri katika\(r=R_E\). Kumbuka kwamba α ina mfululizo usio na kipimo wa maadili ambayo inatimiza hali hii. Kila thamani ya\(α\) inawakilisha suluhisho halali (kila mmoja na thamani yake mwenyewe kwa\(A\)). Suluhisho la jumla au la jumla ni jumla ya ufumbuzi huu wote.
   3. Katika\(t=0,\) sisi kudhani kwamba dunia yote ilikuwa katika joto la awali moto\(T_0\) (Kelvin alichukua hii kuwa juu\(7000K\).) Matumizi ya hali hii ya mipaka inahusisha matumizi ya juu zaidi ya coefficients ya Fourier. Kama ilivyoelezwa katika sehemu b. kila thamani ya\(α_n\) inawakilisha suluhisho halali, na suluhisho la jumla ni jumla ya ufumbuzi huu wote. Hii matokeo katika ufumbuzi mfululizo:\[T(r,t)=\left(\dfrac{T_0R_E}{π}\right)\sum_n\dfrac{(−1)^{n−1}}{n}e^{−λn^2t}\dfrac{\sin(α_nr)}{r} \nonumber \] mara\(\; α_n=nπ/R_E\).

Kumbuka jinsi maadili ya\(α_n\) kuja kutoka hali ya mipaka kutumika katika sehemu b. mrefu\(\dfrac{−1^{n−1}}{n}\) ni mara\(A_n\) kwa mara kwa kila mrefu katika mfululizo, kuamua kutoka kwa kutumia njia Fourier. Kuruhusu\(β=\dfrac{π}{R_E}\), kuchunguza masharti machache ya kwanza ya ufumbuzi huu umeonyeshwa hapa na kumbuka jinsi\(λ^2\) katika kielelezo husababisha maneno ya juu kupungua haraka kama muda unavyoendelea:

\[T(r,t)=\dfrac{T_0R_E}{πr}\left(e^{−Kβ^2t}(\sinβr)−\dfrac{1}{2}e^{−4Kβ^2t}(\sin2βr)+\dfrac{1}{3}e^{−9Kβ^2t}(\sin3βr)−\dfrac{1}{4}e^{−16Kβ^2t}(\sin4βr)+\dfrac{1}{5}e^{−25Kβ^2t}(\sin5βr)...\right). \nonumber \]

Karibu na masharti\(t=0,\) mengi ya suluhisho yanahitajika kwa usahihi. Kuingiza maadili kwa conductivity\(K\) na\(β=π/R_E\) kwa muda unakaribia tu maelfu ya miaka, tu maneno machache ya kwanza hufanya mchango mkubwa. Kelvin alihitaji tu kuangalia suluhisho karibu na uso wa Dunia (Kielelezo\(\PageIndex{6}\)) na, baada ya muda mrefu, kuamua ni wakati gani uliotoa kiwango cha joto cha wastani kinachojulikana wakati wa zama zake (\(1°F\)ongezeko kwa kila\(50ft\)). Alichagua tu nyakati mbalimbali na gradient karibu na thamani hii. Katika Kielelezo\(\PageIndex{6}\), ufumbuzi hupangwa na kuongezwa, na joto la\(300−K\) uso limeongezwa. Kumbuka kuwa katikati ya Dunia itakuwa baridi. Wakati huo, ilifikiriwa Dunia lazima iwe imara.

Kielelezo\(\PageIndex{6}\): Joto dhidi ya umbali radial kutoka katikati ya Dunia. (a) Matokeo ya Kelvin, yalipanga kupanga. (b) Karibu ya matokeo kwa kina cha\(4.0\) maili chini ya uso wa dunia.

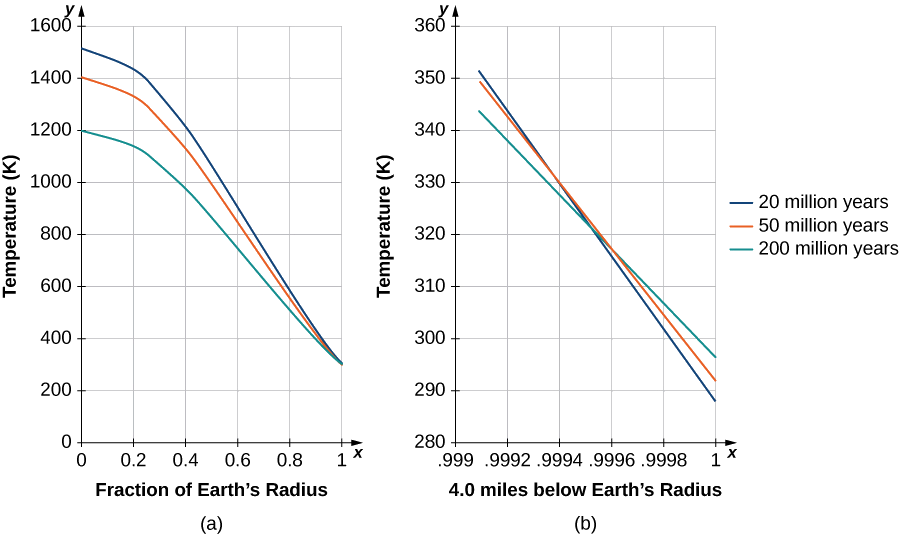
Epilog

Tarehe 20 Mei 1904, mwanafizikia Ernest Rutherford alizungumza katika Taasisi ya Royal kutangaza hesabu iliyorekebishwa iliyojumuisha mchango wa mionzi kama chanzo cha joto la Dunia. Kwa maneno ya Rutherford mwenyewe:

“Mimi alikuja katika chumba, ambayo ilikuwa nusu-giza, na sasa nimemwona Bwana Kelvin katika watazamaji, na kutambua kwamba nilikuwa katika shida katika sehemu ya mwisho ya hotuba yangu kushughulika na umri wa dunia, ambapo maoni yangu yalichangana na yake. Kwa misaada yangu, Kelvin alilala usingizi, lakini nilipofika kwenye hatua muhimu, niliona ndege wa zamani ameketi, kufungua jicho na jogoo mtazamo mzuri kwangu.

Kisha msukumo wa ghafla ulikuja, na nikasema Bwana Kelvin alikuwa mdogo umri wa Dunia, isipokuwa hakuna chanzo kipya [cha joto] kilichogunduliwa. Maneno hayo ya kinabii yalielezea kile tunachokiangalia leo leo, radium! Tazama! Mvulana huyo mzee akanijalia.”

Rutherford alihesabu umri wa Dunia wa miaka milioni 500. Thamani iliyokubaliwa ya leo ya umri wa Dunia ni takriban miaka bilioni 4.6.

Dhana muhimu

• Derivative ya sehemu ni derivative inayohusisha kazi ya kutofautiana zaidi ya moja ya kujitegemea.
• Ili kuhesabu derivative ya sehemu kuhusiana na kutofautiana iliyotolewa, kutibu vigezo vingine vyote kama vipindi na kutumia sheria za kawaida za kutofautisha.
• Derivatives ya sehemu ya juu ya utaratibu inaweza kuhesabiwa kwa njia sawa na derivatives ya juu.

Mlinganyo muhimu

Nusu derivative ya kuhusiana\(f\) na\(x\)\[\dfrac{∂f}{∂x}=\displaystyle{\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h}} \nonumber \]

Nusu derivative ya kuhusiana\(f\) na\(y\)\[\dfrac{∂f}{∂y}=\displaystyle{\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}} \nonumber \]

faharasa

derivatives ya sehemu ya juu

ili pili au sehemu ya juu derivatives, bila kujali kama ni mchanganyiko sehemu derivatives

mchanganyiko sehemu derivatives

derivatives ya pili au ya juu ya sehemu, ambayo angalau mbili ya tofauti ni kuhusiana na vigezo tofauti

derivative sehemu

derivative ya kazi ya variable zaidi ya moja ya kujitegemea ambayo vigezo vyote lakini moja hufanyika mara kwa mara

sehemu tofauti equation

equation ambayo inahusisha kazi isiyojulikana ya kutofautiana zaidi ya moja ya kujitegemea na moja au zaidi ya derivatives yake ya sehemu