14.2E: Mazoezi ya Sehemu ya 14.2

Last updated
Save as PDF

Page ID: 178677

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Matumizi ya sheria kikomo kwa ajili ya kazi ya vigezo mbili kutathmini kila kikomo chini, kutokana$\displaystyle \lim_{(x,y)→(a,b)}f(x,y) = 5$ na kwamba na$\displaystyle \lim_{(x,y)→(a,b)}g(x,y) = 2$.

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right]$

Jibu

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right] = \displaystyle \lim_{(x,y)→(a,b)}f(x,y) + \displaystyle \lim_{(x,y)→(a,b)}g(x,y)= 5 + 2 = 7$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right] =\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right) = 5(2) = 10$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right] = \frac{7\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}g(x,y)}=\frac{7(5)}{2} = 17.5$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right] = \frac{2\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) - 4 \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}f(x,y) - \displaystyle \lim_{(x,y)→(a,b)}g(x,y)}= \frac{2(5) - 4(2)}{5 - 2} = \frac{2}{3}$

Katika mazoezi 2 - 4, pata kikomo cha kazi.

2)$\displaystyle \lim_{(x,y)→(1,2)}x$

3)$\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Jibu: $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2} = 2$

4) Onyesha kwamba kikomo$\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ kipo na ni sawa kwenye njia:$y$ -axis na$x$ -axis, na kando$ y=x$.

Katika mazoezi ya 5 - 19, tathmini mipaka katika maadili yaliyoonyeshwa ya$x$ na$y$. Ikiwa kikomo haipo, sema hili na ueleze kwa nini kikomo haipo.

5)$\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Jibu: $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6} = \frac{2}{3} $

6)$\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

7)$\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x}$

Jibu: $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x} = 1$

8)$\displaystyle \lim_{(x,y)→(0,0)}\sin(\frac{x^8+y^7}{x−y+10})$

9)$\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}$

Jibu: $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}=\frac{1}{2}$

10)$\displaystyle \lim_{(x,y)→(0,π/4)}\frac{\sec x+2}{3x−\tan y}$

11)$\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Jibu: $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y}) = −\frac{1}{2}$

12)$\displaystyle \lim_{(x,y)→(4,4)}x\ln y$

13)$\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Jibu: $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2} = e^{−32}$

14)$\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

15)$\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Jibu: $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y) = 11$

16)$\displaystyle \lim_{(x,y)→(π,π)}x\sin(\frac{x+y}{4})$

17)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Jibu: $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1} = 1$

18)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

19)$\displaystyle \lim_{(x,y)→(0,0)}\ln(x^2+y^2)$

Jibu: Kikomo haipo kwa sababu wakati$x$ na$y$ wote wawili wanakaribia sifuri, kazi inakaribia$ \ln 0$, ambayo haijulikani (inakaribia infinity hasi).

Katika mazoezi 20 - 21, kukamilisha taarifa.

20) Hatua$ (x_0,y_0)$ katika kanda ya ndege$ R$ ni hatua ya ndani ya$R$ kama _________________.

21) Hatua$ (x_0,y_0)$ katika kanda ya ndege$R$ inaitwa hatua ya mipaka ya$R$ kama ___________.

Jibu: Kila disk wazi katikati katika$ (x_0,y_0)$ ina pointi ndani$ R$ na nje$ R$.

Katika mazoezi 22 - 25, tumia mbinu za algebraic kutathmini kikomo.

22)$\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

23)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Jibu: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2} = 0$

24)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

25)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Jibu: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}} = 0$

Katika mazoezi 26 - 27, tathmini mipaka ya kazi za vigezo vitatu.

26)$\displaystyle \lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

27)$\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Jibu: Kikomo haipo.

Katika mazoezi 28 - 31, tathmini kikomo cha kazi kwa kuamua thamani kazi inakaribia kwenye njia zilizoonyeshwa. Ikiwa kikomo haipo, eleza kwa nini sio.

28)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a Pamoja na$x$ -axis$ (y=0)$

b Pamoja na$y$ -axis$ (x=0)$

c. njiani$y=2x$

29) Tathmini$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ kutumia matokeo ya tatizo la awali.

Jibu: Kikomo haipo. Kazi inakaribia maadili mawili tofauti kwa njia tofauti.

30)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a Pamoja na$x$ -axis$ (y=0)$

b Pamoja na$y$ -axis$ (x=0)$

c. njiani$y=x^2$

31) Tathmini$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ kutumia matokeo ya tatizo la awali.

Jibu: Kikomo haipo kwa sababu kazi inakaribia maadili mawili tofauti kwenye njia.

Katika mazoezi 32 - 35, jadili uendelezaji wa kila kazi. Pata eneo kubwa zaidi katika$xy$ -ndege ambayo kila kazi inaendelea.

32)$ f(x,y)=\sin(xy)$

33)$ f(x,y)=\ln(x+y)$

Jibu: Kazi$ f$ inaendelea katika kanda$ y>−x.$

34)$ f(x,y)=e^{3xy}$

35)$ f(x,y)=\dfrac{1}{xy}$

Jibu: Kazi$f$ inaendelea wakati wote katika$xy$ -ndege isipokuwa kwa pointi kwenye$x$ - na$y$ -axes.

Katika mazoezi 36 - 38, tambua kanda ambayo kazi inaendelea. Eleza jibu lako.

36)$ f(x,y)=\dfrac{x^2y}{x^2+y^2}$

37)$ f(x,y)=$$ \begin{cases}\dfrac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

Kidokezo:: Onyesha kwamba kazi inakaribia maadili tofauti pamoja na njia mbili tofauti.

Jibu: kazi ni kuendelea katika$ (0,0)$ tangu kikomo ya kazi katika$ (0,0)$ ni$ 0$, thamani sawa ya$ f(0,0).$

38)$ f(x,y)=\dfrac{\sin(x^2+y^2)}{x^2+y^2}$

39) Kuamua kama$ g(x,y)=\dfrac{x^2−y^2}{x^2+y^2}$ ni kuendelea katika$ (0,0)$.

Jibu: kazi ni$ (0,0).$ discontinuous katika kikomo katika$ (0,0)$ inashindwa kuwepo na$ g(0,0)$ haipo.

40) Unda njama kwa kutumia programu ya graphing ili kuamua ambapo kikomo haipo. Kuamua eneo la ndege ya kuratibu ambayo$ f(x,y)=\dfrac{1}{x^2−y}$ inaendelea.

41) Kuamua eneo la$xy$ ndege ambayo kazi ya composite$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ inaendelea. Tumia teknolojia ili kuunga mkono hitimisho lako.

Jibu: Tangu kazi$ \arctan x$ ni kuendelea juu$ (−∞,∞), g(x,y)=\arctan(\frac{xy^2}{x+y})$ ya kuendelea ambapo$ z=\dfrac{xy^2}{x+y}$ ni kuendelea. kazi ya ndani$ z$ ni kuendelea juu ya pointi zote za$xy$ -ndege isipokuwa pale$ y=−x.$ Hivyo,$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ ni kuendelea juu ya pointi zote za kuratibu ndege ila katika maeneo ambayo$ y=−x.$

42) Kuamua eneo la$xy$ ndege ambalo$ f(x,y)=\ln(x^2+y^2−1)$ linaendelea. Tumia teknolojia ili kuunga mkono hitimisho lako. (Kidokezo: Chagua maadili mbalimbali$ x$ na kwa$ y$ makini!)

43) Ni pointi gani katika nafasi$ g(x,y,z)=x^2+y^2−2z^2$ inayoendelea?

Jibu: All pointi$ P(x,y,z)$ katika nafasi

44) Ni pointi gani katika nafasi$ g(x,y,z)=\dfrac{1}{x^2+z^2−1}$ inayoendelea?

45) Onyesha kwamba$\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ haipo$ (0,0)$ kwa kupanga mipangilio ya kazi.

Jibu

Grafu huongezeka bila kufungwa kama$ x$ na njia$ y$ zote mbili zero.

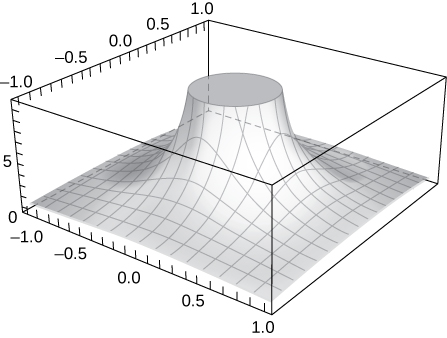
$Grafu ya uso ambapo z-kuratibu huongezeka bila kufungwa kama hatua ya pembejeo (x, y) inakaribia asili.$

46) [T] Tathmini$\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ kwa kupanga njama kazi kwa kutumia CAS. Kuamua analytically kikomo kando ya njia$ x=y^2.$

47) [T]

a Matumizi CAS kuteka contour ramani ya$ z=\sqrt{9−x^2−y^2}$.

b Jina la sura ya kijiometri ya curves ngazi ni nini?

c Kutoa equation ya jumla ya curves ngazi.

d. ni thamani ya juu ya$ z$ nini?

e Ni uwanja gani wa kazi?

f Ni aina gani ya kazi?

Jibu

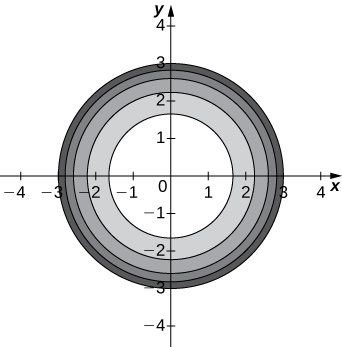
$Ramani ya mpangilio wa kazi z=sqrt {9,1x^2,1y ^2}$

b. curves ngazi ni duru unaozingatia katika$ (0,0)$ na Radius$ 9−c$.
c.$ x^2+y^2=9−c$
d.$ z=3$
e.$ \{(x,y)∈R^2∣x^2+y^2≤9\}$
f.$ \{z|0≤z≤3\}$

48) Kweli au Uongo: Ikiwa$\displaystyle \lim_{(x,y)→(0,0)}f(x)$ tunatathmini njia kadhaa na kila wakati kikomo ni$ 1$, tunaweza kuhitimisha kwamba$\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

49) Tumia kuratibu za polar kupata$\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ Unaweza pia kupata kikomo kwa kutumia utawala wa L'Hôpital.

Jibu: $\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}} = 1$

50) Tumia viwianishi vya polar kupata$\displaystyle \lim_{(x,y)→(0,0)}\cos(x^2+y^2).$

51) Jadili mwendelezo wa$ f(g(x,y))$ wapi$ f(t)=1/t$ na$ g(x,y)=2x−5y.$

Jibu: $ f(g(x,y))$ni kuendelea katika pointi zote$ (x,y)$ ambazo si kwenye mstari$ 2x−5y=0.$

52) Kupewa$ f(x,y)=x^2−4y,$ kupata$\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

53) Kupewa$ f(x,y)=x^2−4y,$ kupata$\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Jibu: $ \displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h} = 2$

Wachangiaji

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created problem 1.