14.2: Mipaka na Mwendelezo

Malengo ya kujifunza

• Tumia kikomo cha kazi ya vigezo viwili.
• Jifunze jinsi kazi ya vigezo viwili inaweza kufikia maadili tofauti katika hatua ya mipaka, kulingana na njia ya mbinu.
• Hali ya masharti ya mwendelezo wa kazi ya vigezo viwili.
• Thibitisha mwendelezo wa kazi ya vigezo viwili katika hatua.
• Tumia kikomo cha kazi ya vigezo vitatu au zaidi na uhakikishe mwendelezo wa kazi kwa hatua.

Sisi sasa kuchunguza kazi ya variable zaidi ya moja na kuona jinsi ya grafu yao. Katika sehemu hii, tunaona jinsi ya kuchukua kikomo cha kazi ya variable zaidi ya moja, na nini maana kwa kazi ya variable zaidi ya moja kuwa kuendelea katika hatua katika uwanja wake. Ni zinageuka dhana hizi kuwa na mambo ambayo si tu kutokea na kazi ya variable moja.

Kikomo cha Kazi ya Vigezo viwili

Kumbuka kutoka Sehemu ya 2.5 kwamba ufafanuzi wa kikomo cha kazi ya variable moja:

Hebu\(f(x)\) kuelezwa kwa wote\(x≠a\) katika kipindi cha wazi kilicho na\(a\). Hebu\(L\) kuwa idadi halisi. Kisha

\[\lim_{x→a}f(x)=L \nonumber \]

kama kwa kila\(ε>0,\) kuna\(δ>0\), kama kwamba kama\(0<|x−a|<δ\) kwa wote\(x\) katika uwanja wa\(f\), basi

\[|f(x)−L|<ε. \nonumber \]

Kabla ya tunaweza kukabiliana ufafanuzi huu kufafanua kikomo cha kazi ya vigezo viwili, sisi kwanza haja ya kuona jinsi ya kupanua wazo la muda wazi katika variable moja kwa muda wazi katika vigezo mbili.

Ufafanuzi:\(\delta\) Disks

Fikiria uhakika\(δ\) Disk\((a,b)∈\mathbb{R}^2.\) iliyozingatia kwa uhakika\((a,b)\) inaelezwa kuwa diski ya wazi ya radius\(δ\) iliyozingatia hatua\((a,b)\) - yaani,

\[\{(x,y)∈\mathbb{R}^2∣(x−a)^2+(y−b)^2<δ^2\} \nonumber \]

kama inavyoonekana katika Kielelezo\(\PageIndex{1}\).

Kielelezo\(\PageIndex{1}\):\(δ\) Disk iliyozingatia karibu na hatua\((2,1)\).

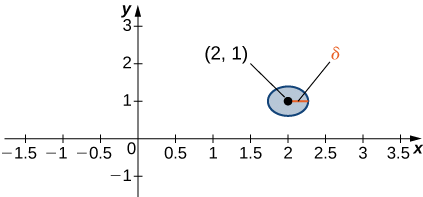
Wazo la\(δ\) disk linaonekana katika ufafanuzi wa kikomo cha kazi ya vigezo viwili. Ikiwa\(δ\) ni ndogo, basi pointi zote\((x,y)\) kwenye\(δ\) diski ziko karibu\((a,b)\). Hii ni sawa kabisa na x kuwa karibu na katika ufafanuzi wa kikomo cha kazi ya variable moja. Kwa mwelekeo mmoja, tunaelezea kizuizi hiki kama

\[a−δ<a+δ.>/span>

Kwa zaidi ya mwelekeo mmoja, tunatumia\(δ\) diski.

Ufafanuzi: kikomo cha kazi ya vigezo viwili

Hebu\(f\) kuwa kazi ya vigezo mbili,\(x\) na\(y\). Kikomo cha\((x,y)\) mbinu\(f(x,y)\) kama\((a,b)\) ni\(L\), imeandikwa

\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]

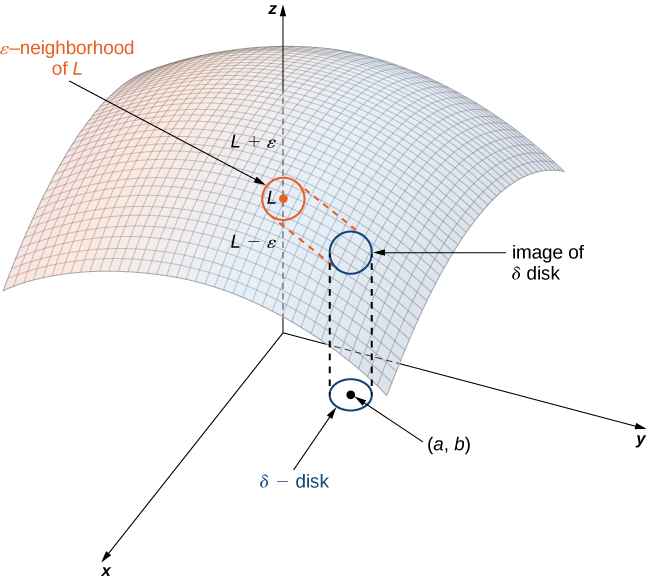
ikiwa kwa kila\(ε>0\) kuna ndogo ndogo ya kutosha\(δ>0\) kwamba kwa pointi\((x,y)\) zote\(δ\) kwenye diski karibu\((a,b)\), isipokuwa labda kwa\((a,b)\) yenyewe, thamani ya\(f(x,y)\) si zaidi ya\(ε\) mbali na\(L\) (Kielelezo\(\PageIndex{2}\)).

Kutumia alama, tunaandika zifuatazo: Kwa chochote\(ε>0\), kuna idadi\(δ>0\) kama hiyo

\[|f(x,y)−L|<ε \nonumber \]

wakati wowote

\[0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]

Kielelezo\(\PageIndex{2}\): kikomo ya kazi kuwashirikisha vigezo mbili inahitaji\(f(x,y)\) kuwa ndani\(ε\) ya\(L\) wakati wowote\((x,y)\) ni ndani\(δ\) ya\((a,b)\). ndogo thamani ya\(ε\), ndogo thamani ya\(δ\).

Kuthibitisha kwamba kikomo ipo kwa kutumia ufafanuzi wa kikomo cha kazi ya vigezo mbili inaweza kuwa changamoto. Badala yake, tunatumia theorem ifuatayo, ambayo inatupa njia za mkato ili kupata mipaka. Fomu katika theorem hii ni ugani wa formula katika theorem ya sheria za kikomo katika Sheria za Limit.

Kupunguza sheria kwa ajili ya kazi ya vigezo viwili

Hebu\(f(x,y)\) na\(g(x,y)\) kuelezwa kwa wote\((x,y)≠(a,b)\) katika kitongoji karibu\((a,b)\), na kudhani kitongoji ni zilizomo kabisa ndani ya uwanja wa\(f\). Kudhani kwamba\(L\) na\(M\) ni idadi halisi kama

\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]

na

\[\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber \]

na basi\(c\) iwe mara kwa mara. Kisha kila moja ya kauli zifuatazo ana:

Sheria ya mara kwa mara:

\[\lim_{(x,y)→(a,b)}c=c \nonumber \]

Sheria ya Identity:

\[\lim_{(x,y)→(a,b)}x=a \nonumber \]

\[\lim_{(x,y)→(a,b)}y=b \nonumber \]

Sheria ya jumla:

\[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber \]

Sheria tofauti:

\[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber \]

Sheria nyingi za mara kwa mara:

\[\lim_{(x,y)→(a,b)}(cf(x,y))=cL \nonumber \]

Sheria ya bidhaa:

\[\lim_{(x,y)→(a,b)}(f(x,y)g(x,y))=LM \nonumber \]

Sheria ya Quotient:

\[\lim_{(x,y)→(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{L}{M} \text{ for } M≠0 \nonumber \]

Sheria ya Nguvu:

\[\lim_{(x,y)→(a,b)}(f(x,y))^n=L^n \nonumber \]

kwa integer yoyote chanya\(n\).

Sheria ya mizizi:

\[\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber \]

kwa ajili ya wote\(L\) kama\(n\) ni isiyo ya kawaida na chanya, na kwa ajili ya\(L≥0\) kama n ni hata na chanya.

Ushahidi wa mali hizi ni sawa na wale kwa mipaka ya kazi za kutofautiana moja. Tunaweza kutumia sheria hizi kutafuta mipaka ya kazi mbalimbali.

Mfano\(\PageIndex{1}\): Finding the Limit of a Function of Two Variables

Pata kila moja ya mipaka ifuatayo:

1. \(\displaystyle \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\)
2. \(\displaystyle \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y}\)

Suluhisho

a. matumizi ya kwanza jumla na tofauti sheria kutenganisha masharti:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\\ = \left(\lim_{(x,y)→(2,−1)}x^2 \right)− \left(\lim_{(x,y)→(2,−1)}2xy \right)+ \left(\lim_{(x,y)→(2,−1)}3y^2 \right)−\left(\lim_{(x,y)→(2,−1)}4x\right) \\ + \left(\lim_{(x,y)→(2,−1)}3y \right)−\left(\lim_{(x,y)→(2,−1)}6\right). \end{align*}\]

Kisha, tumia sheria nyingi mara kwa mara kwenye mipaka ya pili, ya tatu, ya nne, na ya tano:

\[\begin{align*} =(\lim_{(x,y)→(2,−1)}x^2)−2(\lim_{(x,y)→(2,−1)}xy)+3(\lim_{(x,y)→(2,−1)}y^2)−4(\lim_{(x,y)→(2,−1)}x) \\[4pt] +3(\lim_{(x,y)→(2,−1)}y)−\lim_{(x,y)→(2,−1)}6.\end{align*}\]

Sasa, tumia sheria ya nguvu kwenye mipaka ya kwanza na ya tatu, na sheria ya bidhaa kwenye kikomo cha pili:

\[\begin{align*} \left(\lim_{(x,y)→(2,−1)}x\right)^2−2\left(\lim_{(x,y)→(2,−1)}x\right) \left(\lim_{(x,y)→(2,−1)}y\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)^2 \\ −4\left(\lim_{(x,y)→(2,−1)}x\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)−\lim_{(x,y)→(2,−1)}6. \end{align*}\]

Mwisho, tumia sheria za utambulisho kwenye mipaka sita ya kwanza na sheria ya mara kwa mara kwenye kikomo cha mwisho:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6) = (2)^2−2(2)(−1)+3(−1)^2−4(2)+3(−1)−6 \\[4pt] =−6. \end{align*}\]

b Kabla ya kutumia sheria ya quotient, tunahitaji kuthibitisha kuwa kikomo cha denominator ni nonzero. Kwa kutumia sheria tofauti, sheria ya mara kwa mara nyingi, na sheria ya utambulisho,

\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2,−1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}\]

Kwa kuwa kikomo cha denominator ni nonzero, sheria ya quotient inatumika. Sasa tunahesabu kikomo cha nambari kwa kutumia sheria tofauti, sheria nyingi za mara kwa mara, na sheria ya utambulisho:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}\]

Kwa hiyo, kwa mujibu wa sheria quotient tuna

\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2,−1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. \end{align*}\]

Zoezi\(\PageIndex{1}\):

Tathmini kikomo kinachofuata:

\[\lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}. \nonumber \]

Kidokezo

Tumia sheria za kikomo.

Jibu

\[\displaystyle \lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}=\dfrac{3}{2} \nonumber \]

Kwa kuwa tunachukua kikomo cha kazi ya vigezo viwili, hatua\((a,b)\) iko\(\mathbb{R}^2\), na inawezekana kufikia hatua hii kutoka kwa idadi isiyo na kipimo cha maelekezo. Wakati mwingine wakati wa kuhesabu kikomo, jibu linatofautiana kulingana na njia iliyochukuliwa kuelekea\((a,b)\). Ikiwa ndio kesi, basi kikomo kinashindwa kuwepo. Kwa maneno mengine, kikomo lazima iwe cha kipekee, bila kujali njia iliyochukuliwa.

Mfano\(\PageIndex{2}\): Limits That Fail to Exist

Onyesha kwamba hakuna mipaka ifuatayo haipo:

1. \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{2xy}{3x^2+y^2}\)
2. \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4}\)

Suluhisho

a. uwanja wa kazi\(f(x,y)=\dfrac{2xy}{3x^2+y^2}\) lina pointi zote katika\(xy\) -plane isipokuwa kwa uhakika\((0,0)\) (Kielelezo\(\PageIndex{3}\)). Ili kuonyesha kwamba kikomo haipo kama\((x,y)\) mbinu\((0,0)\), tunaona kwamba haiwezekani kukidhi ufafanuzi wa kikomo cha kazi ya vigezo viwili kwa sababu ya ukweli kwamba kazi inachukua maadili tofauti pamoja na mistari tofauti inayopitia hatua\((0,0)\). Kwanza, fikiria mstari\(y=0\) katika\(xy\) -ndege. Kubadilisha\(y=0\) katika\(f(x,y)\) anatoa

\[f(x,0)=\dfrac{2x(0)}{3x^2+0^2}=0 \nonumber \]

kwa thamani yoyote ya\(x\). Kwa hiyo thamani ya\(f\) mabaki ya mara kwa mara kwa hatua yoyote juu ya\(x\) -axis, na kama\(y\) inakaribia sifuri, kazi inabakia fasta kwenye sifuri.

Kisha, fikiria mstari\(y=x\). Kubadilisha\(y=x\) katika\(f(x,y)\) anatoa

\[f(x,x)=\dfrac{2x(x)}{3x^2+x^2}=\dfrac{2x^2}{4x^2}=\tfrac{1}{2}. \nonumber \]

Hii ni kweli kwa hatua yoyote kwenye mstari\(y=x\). Kama sisi basi\(x\) mbinu zero wakati kukaa juu ya mstari huu, thamani ya kazi bado fasta katika\(\tfrac{1}{2}\), bila kujali jinsi ndogo\(x\) ni.

Chagua thamani kwa ε ambayo ni chini ya\(1/2\) -sema,\(1/4\). Kisha, bila kujali\(δ\) disk ndogo tunayozunguka\((0,0)\), maadili ya\(f(x,y)\) pointi ndani ya\(δ\) diski hiyo itajumuisha wote\(0\) na\(\tfrac{1}{2}\). Kwa hiyo, ufafanuzi wa kikomo katika hatua haujawahi kuridhika na kikomo kinashindwa kuwepo.

Kielelezo\(\PageIndex{3}\): Grafu ya kazi\(f(x,y)=\dfrac{2xy}{3x^2+y^2}.\) Pamoja na mstari\(y=0\), kazi ni sawa na sifuri; pamoja na mstari\(y=x\), kazi ni sawa na\(\tfrac{1}{2}\).

b Kwa mtindo sawa na a., tunaweza kufikia asili pamoja na mstari wowote wa moja kwa moja unaopita kupitia asili. Ikiwa tunajaribu\(x\) -axis (yaani,\(y=0\)), basi kazi inabakia fasta kwenye sifuri. Vile vile ni kweli kwa\(y\) -axis. Tuseme tunakaribia asili pamoja na mstari wa moja kwa moja wa mteremko\(k\). Equation ya mstari huu ni\(y=kx\). Kisha kikomo kinakuwa

\[\begin{align*} \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4x(kx)^2}{x^2+3(kx)^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4k^2x^3}{x^2+3k^4x^4} \\ =\lim_{(x,y)→(0,0)}\dfrac{4k^2x}{1+3k^4x^2} \\ = \dfrac{\displaystyle \lim_{(x,y)→(0,0)}(4k^2x)}{\displaystyle \lim_{(x,y)→(0,0)}(1+3k^4x^2)} \\ = 0. \end{align*}\]

bila kujali thamani ya\(k\). Inaonekana kwamba kikomo ni sawa na sifuri. Nini kama sisi alichagua Curve kupita kwa njia ya asili badala? Kwa mfano, tunaweza kufikiria parabola iliyotolewa na equation\(x=y^2\). Kubadilisha\(y^2\) katika nafasi ya\(x\) katika\(f(x,y)\) anatoa

\[\begin{align*}\lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4(y^2)y^2}{(y^2)^2+3y^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4y^4}{y^4+3y^4} \\ = \lim_{(x,y)→(0,0)}1 \\ = 1. \end{align*}\]

Kwa mantiki sawa katika sehemu a, haiwezekani kupata disk δ karibu na asili ambayo inatimiza ufafanuzi wa kikomo kwa thamani yoyote ya\(ε<1.\) Kwa hiyo,

\[\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} \nonumber \]

haipo.

Zoezi\(\PageIndex{2}\):

Onyesha kwamba

\[\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2} \nonumber \]

haipo.

Kidokezo

Chagua mstari na mteremko\(k\) unaopitia hatua\((2,1).\)

Jibu

Kama\(y=k(x−2)+1,\) basi\(\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2}=\dfrac{k}{1+k^2}\). Kwa kuwa jibu linategemea\(k,\) kikomo kinashindwa kuwepo.

Pointi ya Mambo ya Ndani na Pointi

Ili kujifunza mwendelezo na kutofautisha kazi ya vigezo viwili au zaidi, sisi kwanza tunahitaji kujifunza nenosiri jipya.

Ufafanuzi: pointi za ndani na mipaka

Hebu\(S\) kuwa subset ya\(\mathbb{R}^2\) (Kielelezo\(\PageIndex{4}\)).

1. Hatua\(P_0\) inaitwa hatua ya ndani ya\(S\) ikiwa kuna\(δ\) disk iliyozingatia kuzunguka\(P_0\) iliyomo kabisa\(S\).
2. Hatua\(P_0\) inaitwa hatua ya mipaka ya\(S\) ikiwa kila\(δ\) disk inayozingatia karibu\(P_0\) ina pointi zote ndani na nje\(S\).

Kielelezo\(\PageIndex{4}\): Katika seti\(S\) iliyoonyeshwa,\((−1,1)\) ni hatua ya mambo ya ndani na\((2,3)\) ni hatua ya mipaka.

Ufafanuzi: Kufungua na kufungwa seti

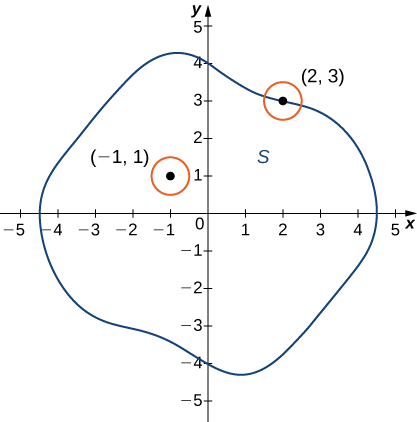
Hebu\(S\) kuwa subset ya\(\mathbb{R}^2\) (Kielelezo\(\PageIndex{4}\)).

1. \(S\)inaitwa kuweka wazi kama kila hatua ya\(S\) ni hatua ya mambo ya ndani.
2. \(S\)inaitwa seti iliyofungwa ikiwa ina pointi zake zote za mipaka.

Mfano wa kuweka wazi ni\(δ\) disk. Ikiwa tunajumuisha mipaka ya diski, basi inakuwa seti iliyofungwa. Seti iliyo na baadhi, lakini sio yote, ya pointi zake za mipaka hazifunguliwe wala kufungwa. Kwa mfano, ikiwa tunajumuisha nusu ya mipaka ya\(δ\) diski lakini sio nusu nyingine, basi kuweka haifunguliwe wala kufungwa.

Ufafanuzi: seti zilizounganishwa na Mikoa

Hebu\(S\) kuwa subset ya\(\mathbb{R}^2\) (Kielelezo\(\PageIndex{4}\)).

1. Seti ya wazi\(S\) ni seti iliyounganishwa ikiwa haiwezi kuwakilishwa kama muungano wa subsets mbili au zaidi, zisizo wazi.
2. Seti\(S\) ni kanda ikiwa ni wazi, imeunganishwa, na sio tupu.

Ufafanuzi wa kikomo cha kazi ya vigezo viwili inahitaji\(δ\) disk kuwa ndani ya uwanja wa kazi. Hata hivyo, ikiwa tunataka kupata kikomo cha kazi kwenye hatua ya mipaka ya kikoa,\(δ\) disk haijawahi ndani ya kikoa. Kwa ufafanuzi, baadhi ya pointi za\(δ\) disk ziko ndani ya kikoa na baadhi ni nje. Kwa hiyo, tunahitaji tu kuzingatia pointi zilizo ndani ya\(δ\) diski zote na uwanja wa kazi. Hii inasababisha ufafanuzi wa kikomo cha kazi katika hatua ya mipaka.

Ufafanuzi

Hebu\(f\) kuwa kazi ya vigezo mbili,\(x\) na\(y\), na tuseme\((a,b)\) ni juu ya mipaka ya uwanja wa\(f\). Kisha, kikomo cha\((x,y)\) mbinu\(f(x,y)\) kama\((a,b)\) ni\(L\), imeandikwa

\[\lim_{(x,y)→(a,b)}f(x,y)=L, \nonumber \]

kama kwa yeyote\(ε>0,\) kuna idadi\(δ>0\) kama kwamba kwa hatua yoyote\((x,y)\) ndani ya uwanja wa\(f\) na ndani ya umbali suitably ndogo chanya\(δ\)\((a,b),\) ya thamani ya\(f(x,y)\) si zaidi ya\(ε\) mbali na\(L\) (Kielelezo\(\PageIndex{2}\)). Kutumia alama, tunaweza kuandika: Kwa chochote\(ε>0\), kuna idadi\(δ>0\) kama hiyo

\[|f(x,y)−L|<ε\, \text{whenever}\, 0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]

Mfano\(\PageIndex{3}\): Limit of a Function at a Boundary Point

Thibitisha

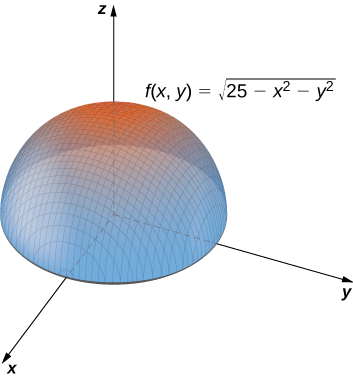
\[\lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2}=0. \nonumber \]

Suluhisho

Kikoa cha kazi\(f(x,y)=\sqrt{25−x^2−y^2}\) ni\(\big\{(x,y)∈\mathbb{R}^2∣x^2+y^2≤25\big\}\), ambayo ni mduara wa radius\(5\) unaozingatia asili, pamoja na mambo yake ya ndani kama inavyoonekana kwenye Mchoro\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\): Domain ya kazi\(f(x,y)=\sqrt{25−x^2−y^2}\).

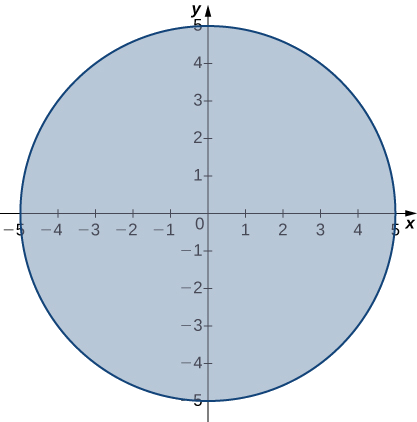
Tunaweza kutumia sheria za kikomo, ambazo zinatumika kwa mipaka katika mipaka ya vikoa pamoja na pointi za mambo ya ndani:

\[\begin{align*} \lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2} =\sqrt{\lim_{(x,y)→(4,3)}(25−x^2−y^2)} \\ = \sqrt{\lim_{(x,y)→(4,3)}25−\lim_{(x,y)→(4,3)}x^2−\lim_{(x,y)→(4,3)}y^2} \\ =\sqrt{25−4^2−3^2} \\ = 0 \end{align*}\]

Angalia grafu ifuatayo.

Kielelezo\(\PageIndex{6}\): Grafu ya kazi\(f(x,y)=\sqrt{25−x^2−y^2}\).

Zoezi\(\PageIndex{3}\)

Tathmini kikomo kinachofuata:

\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2}. \nonumber \]

Kidokezo

Kuamua uwanja wa\(f(x,y)=\sqrt{29−x^2−y^2}\).

Jibu

\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2} \nonumber \]

Kuendelea kwa Kazi za Vigezo viwili

Katika Mwendelezo, tulifafanua mwendelezo wa kazi ya variable moja na tukaona jinsi ilivyotegemea kikomo cha kazi ya variable moja. Hasa, hali tatu ni muhimu\(f(x)\) kwa kuwa kuendelea katika hatua\(x=a\)

1. \(f(a)\)ipo.
2. \(\displaystyle \lim_{x→a}f(x)\)ipo.
3. \(\displaystyle \lim_{x→a}f(x)=f(a).\)

Hali hizi tatu ni muhimu kwa ajili ya mwendelezo wa kazi ya vigezo mbili pia.

Ufafanuzi: Kazi zinazoendelea

Kazi\(f(x,y)\) inaendelea kwa hatua\((a,b)\) katika uwanja wake ikiwa hali zifuatazo zinaridhika:

1. \(f(a,b)\)ipo.
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)ipo.
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)

Mfano\(\PageIndex{4}\): Demonstrating Continuity for a Function of Two Variables

Onyesha kwamba kazi

\[f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber \]

ni kuendelea katika hatua\((5,−3).\)

Suluhisho

Kuna masharti matatu ya kuridhika, kwa ufafanuzi wa mwendelezo. Katika mfano huu,\(a=5\) na\(b=−3.\)

1. \(f(a,b)\)ipo. Hii ni kweli kwa sababu uwanja wa kazi f lina jozi hizo zilizoamriwa ambazo denominator ni nonzero (yaani,\(x+y+1≠0\)). Point\((5,−3)\) inatimiza hali hii. Zaidi ya hayo,

\[f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6}{2+1}=3. \nonumber \]

2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)ipo. Hii pia ni kweli:

\[\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,−3)}\dfrac{3x+2y}{x+y+1} \\ =\dfrac{\displaystyle \lim_{(x,y)→(5,−3)}(3x+2y)}{\displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align*}\]

3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)Hii ni kweli kwa sababu sisi tu umeonyesha kwamba pande zote mbili za equation hii sawa tatu.

Zoezi\(\PageIndex{4}\)

Onyesha kwamba kazi

\[f(x,y)=\sqrt{26−2x^2−y^2}\nonumber \]

ni kuendelea katika hatua\((2,−3)\).

Kidokezo

Tumia ufafanuzi wa sehemu tatu ya kuendelea.

Jibu

1. Domain ya\(f\) ina jozi kuamuru\((2,−3)\) kwa sababu\(f(a,b)=f(2,−3)=\sqrt{16−2(2)^2−(−3)^2}=3\)
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=3\)
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b)=3\)

Kuendelea kwa kazi ya idadi yoyote ya vigezo pia inaweza kuelezwa katika suala la delta na epsilon. kazi ya vigezo mbili ni kuendelea\((x_0,y_0)\) katika hatua katika uwanja wake kama kwa kila\(ε>0\) kuna kuna\(δ>0\) vile kwamba, wakati wowote\(\sqrt{(x−x_0)^2+(y−y_0)^2}<δ\) ni kweli, Ufafanuzi\(|f(x,y)−f(a,b)|<ε.\) huu unaweza kuwa pamoja na ufafanuzi rasmi (yaani, ufafanuzi epsilon-delta) ya mwendelezo ya kazi ya variable moja kuthibitisha theorems zifuatazo:

Jumla ya Kazi za Kuendelea Ni Kuendelea

Kama\(f(x,y)\) ni kuendelea katika\((x_0,y_0)\), na\(g(x,y)\) ni kuendelea katika\((x_0,y_0)\), basi\(f(x,y)+g(x,y)\) ni kuendelea katika\((x_0,y_0)\).

Bidhaa ya Kazi za Kuendelea Inaendelea

Kama\(g(x)\) ni kuendelea katika\(x_0\) na\(h(y)\) ni kuendelea katika\(y_0\), basi\(f(x,y)=g(x)h(y)\) ni kuendelea katika\((x_0,y_0).\)

Muundo wa Kazi za Kuendelea Ni Kuendelea

Hebu\(g\) kuwa kazi ya vigezo mbili kutoka uwanja\(D⊆\mathbb{R}^2\) kwa aina mbalimbali\(R⊆R.\) Tuseme\(g\) ni kuendelea wakati fulani\((x_0,y_0)∈D\) na kufafanua\(z_0=g(x_0,y_0)\). Hebu f kuwa kazi kwamba ramani\(R\) kwa\(R\) vile kwamba\(z_0\) ni katika uwanja wa\(f\). Mwisho, kudhani\(f\) ni kuendelea katika\(z_0\). Kisha\(f∘g\) ni kuendelea katika\((x_0,y_0)\) kama inavyoonekana katika Kielelezo\(\PageIndex{7}\).

Kielelezo\(\PageIndex{7}\): Utungaji wa kazi mbili zinazoendelea ni kuendelea.

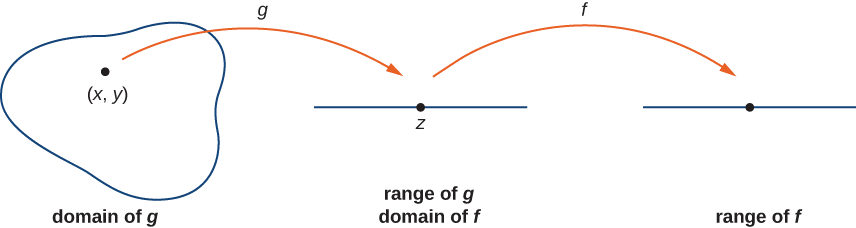
Hebu sasa tutumie theorems zilizopita ili kuonyesha mwendelezo wa kazi katika mifano ifuatayo.

Mfano\(\PageIndex{5}\): More Examples of Continuity of a Function of Two Variables

Onyesha kuwa kazi\(f(x,y)=4x^3y^2\) na\(g(x,y)=\cos(4x^3y^2)\) zinaendelea kila mahali.

Suluhisho

Polynomials\(g(x)=4x^3\) na\(h(y)=y^2\) ni kuendelea katika kila idadi halisi, na kwa hiyo kwa bidhaa ya kazi ya kuendelea theorem,\(f(x,y)=4x^3y^2\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -plane. Kwa kuwa\(f(x,y)=4x^3y^2\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -ndege na\(g(x)=\cos x\) ni kuendelea katika kila idadi halisi\(x\), mwendelezo wa muundo wa kazi inatuambia kwamba\(g(x,y)=\cos(4x^3y^2)\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -plane.

Zoezi\(\PageIndex{5}\)

Onyesha kuwa kazi\(f(x,y)=2x^2y^3+3\) na\(g(x,y)=(2x^2y^3+3)^4\) zinaendelea kila mahali.

Kidokezo

Tumia mwendelezo wa jumla, bidhaa, na muundo wa kazi mbili.

Jibu

Polynomials\(g(x)=2x^2\) na\(h(y)=y^3\) ni kuendelea katika kila idadi halisi; Kwa hiyo, kwa bidhaa ya kazi zinazoendelea theorem,\(f(x,y)=2x^2y^3\) inaendelea kila hatua\((x,y)\) katika\(xy\) -plane. Zaidi ya hayo, kazi yoyote ya mara kwa mara ni kuendelea kila mahali, hivyo\(g(x,y)=3\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -plane. Kwa hiyo,\(f(x,y)=2x^2y^3+3\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -ndege. Mwisho,\(h(x)=x^4\) ni kuendelea katika kila idadi halisi\(x\), hivyo kwa mwendelezo wa kazi Composite theorem\(g(x,y)=(2x^2y^3+3)^4\) ni kuendelea katika kila hatua\((x,y)\) katika\(xy\) -plane.

Kazi ya Vigezo Tatu au Zaidi

Kikomo cha kazi ya vigezo tatu au zaidi hutokea kwa urahisi katika programu. Kwa mfano, tuseme tuna kazi\(f(x,y,z)\) ambayo inatoa joto katika eneo la kimwili\((x,y,z)\) katika vipimo vitatu. Au labda kazi\(g(x,y,z,t)\) inaweza kuonyesha shinikizo la hewa mahali kwa\((x,y,z)\) wakati\(t\). Tunawezaje kuchukua kikomo katika hatua katika\(\mathbb{R}^3\)? Ina maana gani kuendelea kwa hatua katika vipimo vinne?

Majibu ya maswali haya yanategemea kupanua dhana ya\(δ\) diski katika vipimo zaidi ya mbili. Kisha, mawazo ya kikomo ya kazi ya vigezo tatu au zaidi na mwendelezo wa kazi ya vigezo tatu au zaidi ni sawa na ufafanuzi uliotolewa mapema kwa kazi ya vigezo viwili.

Ufafanuzi:\(δ\)-balls

Hebu\((x_0,y_0,z_0)\) kuwa hatua katika\(\mathbb{R}^3\). Kisha,\(δ\) -ball katika vipimo vitatu lina pointi zote katika\(\mathbb{R}^3\) uongo katika umbali wa chini ya\(δ\) kutoka\((x_0,y_0,z_0)\) -yaani,

\[\big\{(x,y,z)∈\mathbb{R}^3∣\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]

Ili kufafanua\(δ\) -mpira katika vipimo vya juu, ongeza masharti ya ziada chini ya radical ili kuendana na kila mwelekeo wa ziada. Kwa mfano, kutokana na hatua\(P=(w_0,x_0,y_0,z_0)\) katika\(\mathbb{R}^4\),\(δ\) mpira kuzunguka\(P\) unaweza kuelezewa na

\[\big\{(w,x,y,z)∈\mathbb{R}^4∣\sqrt{(w−w_0)^2+(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]

Ili kuonyesha kwamba kikomo cha kazi ya vigezo vitatu ipo katika hatua\((x_0,y_0,z_0)\), inatosha kuonyesha kwamba kwa hatua yoyote katika\(δ\) mpira unaozingatia saa\((x_0,y_0,z_0)\), thamani ya kazi katika hatua hiyo ni kiholela karibu na thamani ya kudumu (thamani ya kikomo). Sheria zote kikomo kwa ajili ya kazi ya vigezo mbili kushikilia kwa ajili ya kazi ya vigezo zaidi ya mbili pia.

Mfano\(\PageIndex{6}\): Finding the Limit of a Function of Three Variables

Kupata

\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}. \nonumber \]

Suluhisho

Kabla ya kutumia sheria ya quotient, tunahitaji kuthibitisha kwamba kikomo cha denominator ni nonzero. Kwa kutumia sheria tofauti, sheria ya utambulisho, na sheria ya mara kwa mara,

\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y)−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{align*}\]

Kwa kuwa hii ni nonzero, sisi ijayo kupata kikomo cha nambari. Kutumia sheria ya bidhaa, sheria ya nguvu, sheria tofauti, sheria nyingi za mara kwa mara, na sheria ya utambulisho,

\[\begin{align*} \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z) =(\lim_{(x,y,z)→(4,1,−3)}x)^2(\lim_{(x,y,z)→(4,1,−3)}y)−3\lim_{(x,y,z)→(4,1,−3)}z \\ =(4^2)(1)−3(−3) \\ = 16+9 \\ = 25 \end{align*}\]

Mwisho, kutumia sheria ya quotient:

\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}=\dfrac{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z)}{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(2x+5y−z)}=\dfrac{25}{16} \nonumber \]

Zoezi\(\PageIndex{6}\)

Kupata

\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2} \nonumber \]

Kidokezo

Tumia sheria za kikomo na uendelezaji wa muundo wa kazi.

Jibu

\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2}=2 \nonumber \]

Dhana muhimu

• Ili kujifunza mipaka na kuendelea kwa kazi za vigezo viwili, tunatumia\(δ\) diski inayozingatia karibu na hatua fulani.
• kazi ya vigezo kadhaa ina kikomo kama kwa hatua yoyote katika\(δ\) mpira unaozingatia katika hatua\(P\), thamani ya kazi katika hatua hiyo ni kiholela karibu na thamani fasta (thamani kikomo).
• Sheria za kikomo zilizoanzishwa kwa kazi ya variable moja zina upanuzi wa asili kwa kazi za kutofautiana zaidi ya moja.
• Kazi ya vigezo viwili ni kuendelea katika hatua kama kikomo ipo katika hatua hiyo, kazi ipo katika hatua hiyo, na kikomo na kazi ni sawa katika hatua hiyo.

faharasa

hatua ya mipaka

hatua\(P_0\) ya\(R\) ni hatua ya mipaka ikiwa kila\(δ\) disk inayozunguka\(P_0\) ina pointi ndani na nje\(R\)

kuweka imefungwa

seti\(S\) ambayo ina pointi zake zote za mipaka

kuweka kushikamana

seti ya wazi\(S\) ambayo haiwezi kuwakilishwa kama muungano wa subsets mbili au zaidi, zisizo wazi

\(δ\)diski

disk wazi ya radius\(δ\) iliyozingatia kwa uhakika\((a,b)\)

\(δ\)mpira

pointi zote katika\(\mathbb{R}^3\) uongo katika umbali wa chini ya\(δ\) kutoka\((x_0,y_0,z_0)\)

hatua ya mambo ya ndani

hatua\(P_0\) ya\(\mathbb{R}\) ni hatua ya mipaka ikiwa kuna\(δ\) disk iliyozunguka\(P_0\) iliyo karibu kabisa\(\mathbb{R}\)

kuweka wazi

seti\(S\) ambayo haina sehemu yoyote ya mipaka

mkoa

subset wazi, iliyounganishwa, isiyo na tupu ya\(\mathbb{R}^2\)