14.4E: Mazoezi ya Sehemu ya 14.4

Last updated
Save as PDF

Page ID: 178553

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 2, pata kitengo cha kawaida cha vector kwenye uso kwenye hatua iliyoonyeshwa.

1)$ f(x,y)=x^3,\quad (2,−1,8)$

Jibu: $ (\frac{\sqrt{145}}{145})(12\hat{\mathbf i}−\hat{\mathbf k})$

2)$ \ln\left(\dfrac{x}{y−z}\right)=0$ wakati$ x=y=1$

Katika mazoezi 3 - 7, pata vector ya kawaida na vector tangent kwa uhakika$ P$.

3)$ x^2+xy+y^2=3,\quad P(−1,−1)$

Jibu: Vector ya kawaida:$ \hat{\mathbf i}+\hat{\mathbf j}$, vector tangent:$ \hat{\mathbf i}−\hat{\mathbf j}$

4)$ (x^2+y^2)^2=9(x^2−y^2),\quad P(\sqrt{2},1)$

5)$ xy^2−2x^2+y+5x=6,\quad P(4,2)$

Jibu: Vector ya kawaida:$ 7\hat{\mathbf i}−17\hat{\mathbf j}$, vector tangent:$ 17\hat{\mathbf i}+7\hat{\mathbf j}$

6)$ 2x^3−x^2y^2=3x−y−7,\quad P(1,−2)$

7)$ ze^{x^2−y^2}−3=0, \quad P(2,2,3)$

Jibu: Vector kawaida:$ -12\hat{\mathbf i}+12\hat{\mathbf j}-\hat{\mathbf k}$ au$ 12\hat{\mathbf i}-12\hat{\mathbf j}+\hat{\mathbf k}$,
tangent vector:$ 0\hat{\mathbf i}+1\hat{\mathbf j}+12\hat{\mathbf k}$ au$ 1\hat{\mathbf i}+0\hat{\mathbf j}-12\hat{\mathbf k}$

Katika mazoezi 8 - 19, pata equation kwa ndege ya tangent kwenye uso kwenye hatua iliyoonyeshwa. (Kidokezo: Kama kazi aliyopewa si tayari kutatuliwa kwa$z$, kuanza kwa kutatua kwa$ z$ katika suala la$ x$ na$ y$.)

8)$ −8x−3y−7z=−19,\quad P(1,−1,2)$

9)$ z=−9x^2−3y^2,\quad P(2,1,−39)$

Jibu: $ −36x−6y−z=−39$

10)$ x^2+10xyz+y^2+8z^2=0,\quad P(−1,−1,−1)$

11)$ z=\ln(10x^2+2y^2+1),\quad P(0,0,0)$

Jibu: $ z=0$

12)$ z=e^{7x^2+4y^2}, \quad P(0,0,1)$

13)$ xy+yz+zx=11,\quad P(1,2,3)$

Jibu: $ 5x+4y+3z−22=0$

14)$ x^2+4y^2=z^2,\quad P(3,2,5)$

15)$ x^3+y^3=3xyz,\quad P(1,2,\frac{3}{2})$

Jibu: $ 4x−5y+4z=0$

16)$ z=axy,\quad P(1,\frac{1}{a},1)$

17)$ z=\sin x+\sin y+\sin(x+y),\quad P(0,0,0)$

Jibu: $ 2x+2y−z=0$

18)$ h(x,y)=\ln\sqrt{x^2+y^2},\quad P(3,4)$

19)$ z=x^2−2xy+y^2,\quad P(1,2,1)$

Jibu: $ −2(x−1)+2(y−2)−(z−1)=0$

Katika mazoezi 20 - 25, pata usawa wa parametric kwa mstari wa kawaida kwenye uso kwenye hatua iliyoonyeshwa. (Kumbuka kwamba kupata equation ya mstari katika nafasi, unahitaji uhakika juu ya mstari,$ P_0(x_0,y_0,z_0)$, na vector$ \vecs v=⟨a,b,c⟩$ ambayo ni sambamba na mstari. Kisha equations ya mstari ni:$\quad x=x_0+at,\quad y=y_0+bt, \quad z=z_0+ct.)$

20)$ −3x+9y+4z=−4,\quad P(1,−1,2)$

21)$ z=5x^2−2y^2,\quad P(2,1,18)$

Jibu: $ x=20t+2,y=−4t+1,z=−t+18$

22)$ x^2−8xyz+y^2+6z^2=0,\quad P(1,1,1)$

23)$ z=\ln(3x^2+7y^2+1),\quad P(0,0,0)$

Jibu: $ x=0,y=0,z=t$

24)$ z=e^{4x^2+6y^2},\quad P(0,0,1)$

25)$ z=x^2−2xy+y^2$ katika hatua$ P(1,2,1)$

Jibu: $ x−1=2t;y−2=−2t;z−1=t$

Katika mazoezi 26 - 28, tumia takwimu iliyoonyeshwa hapa.

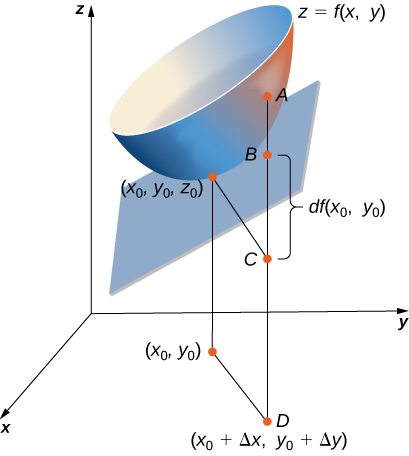
$Mchoro unaonyesha tofauti ya f kwa uhakika (x_0, y_0)$

26) Urefu wa sehemu ya mstari$ AC$ ni sawa na maneno gani ya hisabati?

27) urefu wa sehemu ya mstari$ BC$ ni sawa na maneno gani ya hisabati?

Jibu: Tofauti ya kazi$ z(x,y)=dz=f_xdx+f_ydy$

28) Kutumia takwimu, kuelezea nini urefu wa sehemu ya mstari$ AB$ inawakilisha.

29) Onyesha kwamba$ f(x,y)=e^{xy}x$ ni tofauti katika hatua$ (1,0).$

Jibu: Kutumia ufafanuzi wa kutofautisha, tuna$ e^{xy}x≈x+y$.

30) Onyesha kwamba$ f(x,y)=x^2+3y$ ni tofauti katika kila hatua. Kwa maneno mengine, kuonyesha kwamba$ Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy$, ambapo wote wawili$ ε_1$ na$ ε_2$ mbinu sifuri kama$ (Δx,Δy)$ mbinu$ (0,0).$

Jibu: $ Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0$kwa wadogo$ Δx$ na$ z$ satisfies ufafanuzi wa kutofautisha.

31) Pata tofauti ya jumla ya kila kazi:

$ z=x^3 + y^3 - 5$
$ z=e^{xy}$
$ z=y\cos x+\sin y$
$P = t^2 + 3t + tu^3$
$ w=e^y\cos(x)+z^2$

Majibu:

$ dz = 3x^2\,dx +3y^2\,dy $
$ dz = ye^{xy}\,dx +xe^{xy}\,dy $
$ dz = -y\sin x\,dx +(\cos x + \cos y)\,dy $
$ dP = (2t + 3 + u^3)\, dt + 3t u^2 \,du $
$ dw = -e^y\sin(x)\,dx +e^y\cos(x)\,dy +2z\,dz$

Pata tofauti ya jumla$dz$ ya kazi$ z=\dfrac{xy}{y+x}$ na kisha
b. hali ya thamani yake ambapo$ x$ mabadiliko kutoka$ 10$ kwa$ 10.5$ na$ y$ mabadiliko kutoka$ 15$ kwa$ 13$.

Jibu: a.$ dz = \dfrac{y^2}{(x+y)^2}\, dx + \dfrac{x^2}{(x+y)^2} \,dy $
b.$dx = 0.5$ na$dy = -2$ hivyo

\ (\ kuanza {align*} dz &= f_x (10, 15)\, dx + f_y (10,15)\, dy\\
&=\ Frac {15^2} {25 ^ 2}\, dx +\ frac {10^2} {25^2}\, dy\\
&=\ Frac {225} {625} {625}\, (0.5) +\ frac {100} { 625} (-2)\\
&=\ FRAC {9} {25}\ kushoto (\ Frac {1} {2}\ haki) +\ Frac {4} {25} (-2)\\
&=\ Frac {18} {100} -\ Frac {32} {100} {100}\\
&= .18 - .32 = -0.14\ mwisho {align*}\)

33) Hebu$ z=f(x,y)=xe^y.$ Jimbo tofauti yake ya jumla. Kisha compute$ Δz$ kutoka$ P(1,2)$ kwa$ Q(1.05,2.1)$ na kisha kupata mabadiliko takriban katika$ z$,$dz$, kutoka hatua$ P$ kwa uhakika$ Q$. Kumbuka$ Δz=f(x+Δx,y+Δy)−f(x,y)$,$ dz$ na$ Δz$ lazima iwe takriban sawa, ikiwa$dx$ na wote wawili$dy$ ni ndogo sana.

Jibu: Jumla ya Tofauti:$dz = e^y\,dx + xe^y\, dy $
$ Δz≈1.185422$ na$ dz≈1.108.$ Kumbuka kuwa wao ni karibu sana.

34) Kiasi cha silinda ya mviringo sahihi hutolewa na$ V(r,h)=πr^2h.$ Pata tofauti$ dV$. Tafsiri formula kijiometri.

Jibu: $ dV = 2 \pi r h\, dr + \pi r^2 \,dh $

35) Angalia tatizo lililotangulia. Tumia tofauti ili kukadiria kiasi cha alumini katika alumini iliyofungwa inaweza kwa kipenyo$ 8.0cm$ na urefu$ 12cm$ ikiwa alumini ni$ 0.04$ cm nene.

Jibu: $ 16\,\text{cm}^3$

36) Matumizi tofauti$ dz$ na takriban mabadiliko katika$ z=\sqrt{4−x^2−y^2}$ kama$ (x,y)$ hatua kutoka hatua$ (1,1)$ kwa hatua$ (1.01,0.97).$ Linganisha makadirio haya na mabadiliko halisi katika kazi.

37) Hebu$ z=f(x,y)=x^2+3xy−y^2.$ Tafuta mabadiliko halisi katika kazi na mabadiliko ya takriban katika kazi kama$ x$ mabadiliko kutoka$ 2.00$ kwa$ 2.05$ na$ y$ mabadiliko kutoka$ 3.00$ kwa$ 2.96$.

Jibu: $ Δz=$mabadiliko halisi$ =0.6449$, mabadiliko ya takriban ni$ dz=0.65$. Maadili mawili ni karibu.

38) Kasi ya centripetal ya chembe inayohamia kwenye mduara hutolewa na$ a(r,v)=\frac{v^2}{r},$ wapi$ v$ kasi na$ r$ ni radius ya mduara. Takriban kiwango cha juu cha asilimia kosa katika kupima kasi kutokana na makosa ya$ 3\%$ ndani$ v$ na$ 2\%$ ndani$ r$. (Kumbuka kwamba kosa la asilimia ni uwiano wa kiasi cha kosa juu ya kiasi cha awali. Kwa hiyo, katika kesi hii, kosa la asilimia katika a linatolewa na$ \frac{da}{a}$.)

39) Radius$ r$ na urefu$ h$ wa silinda ya mviringo sahihi hupimwa na makosa iwezekanavyo$ 4\%$ na$ 5\%$, kwa mtiririko huo. Takriban kiwango cha juu cha asilimia kosa katika kupima kiasi (Kumbuka kwamba kosa la asilimia ni uwiano wa kiasi cha kosa juu ya kiasi cha awali. Kwa hiyo, katika kesi hii, kosa la asilimia$ V$ linatolewa na$ \frac{dV}{V}$.)

Jibu: $ 13\%$au$ 0.13$

40) Radius ya msingi na urefu wa koni ya mviringo ya mviringo hupimwa kama$ 10$ ili. na$ 25$ ndani., kwa mtiririko huo, na kosa linalowezekana kwa kipimo cha$ 0.1$ kadri. kila mmoja. Tumia tofauti ili kukadiria kosa la juu katika kiasi kilichohesabiwa cha koni.

41) Upinzani wa umeme$ R$ unaozalishwa na resistors za wiring$ R_1$ na$ R_2$ sambamba unaweza kuhesabiwa kutoka kwa formula$ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$. Ikiwa$ R_1$ na$ R_2$ hupimwa kuwa$ 7Ω$ na$ 6Ω$, kwa mtiririko huo, na kama vipimo hivi ni sahihi ndani$ 0.05Ω$, tathmini kosa la juu linalowezekana katika kompyuta$ R$. (Ishara$ Ω$ inawakilisha ohm, kitengo cha upinzani wa umeme.)

Jibu: $ 0.025$

42) Eneo la ellipse na shaba za urefu$ 2a$ na$ 2b$ hutolewa na formula$ A=πab$. Takriban asilimia mabadiliko katika eneo wakati$ a$ kuongezeka kwa$ 2\%$ na$ b$ kuongezeka kwa$ 1.5\%.$

43) Kipindi$ T$ cha pendulum rahisi na oscillations ndogo ni mahesabu kutoka formula$ T=2π\sqrt{\frac{L}{g}}$, ambapo$ L$ ni urefu wa pendulum na$ g$ ni kuongeza kasi kutokana na mvuto. Tuseme kwamba$ L$ na$ g$ kuwa na makosa ya, kwa zaidi,$ 0.5\%$ na$ 0.1\%$, kwa mtiririko huo. Matumizi differentials takriban upeo asilimia makosa katika thamani mahesabu ya$ T$.

Jibu: $ 0.3\%$

44) Nguvu$ P$ ya umeme hutolewa na$ P=\frac{V^2}{R}$, wapi$ V$ voltage na$ R$ ni upinzani. Takriban kosa la asilimia ya juu katika kuhesabu nguvu ikiwa$ 120 V$ hutumiwa kwa$ 2000−Ω$ kupinga na makosa ya asilimia iwezekanavyo katika kupima$ V$$ 3\%$ na$ R$ ni$ 4\%$, kwa mtiririko huo.

Kwa mazoezi 45 - 49, pata makadirio ya mstari wa kila kazi kwenye hatua iliyoonyeshwa.

45)$ f(x,y)=x\sqrt{y},\quad P(1,4)$

Jibu: $ L(x,y) = 2x+\frac{1}{4}y−1$

46)$ f(x,y)=e^x\cos y;\quad P(0,0)$

47)$ f(x,y)=\arctan(x+2y),\quad P(1,0)$

Jibu: $ L(x,y) = \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}$

48)$ f(x,y)=\sqrt{20−x^2−7y^2},\quad P(2,1)$

49)$ f(x,y,z)=\sqrt{x^2+y^2+z^2},\quad P(3,2,6)$

Jibu: $ L(x,y,z) = \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z$

50) [T] Kupata equation ya ndege tangent kwa uso$ f(x,y)=x^2+y^2$ katika hatua$ (1,2,5),$ na grafu uso na ndege tangent katika hatua.

51) [T] Pata usawa kwa ndege ya tangent kwenye uso kwenye hatua iliyoonyeshwa, na graph uso na ndege ya tangent:$ z=\ln(10x^2+2y^2+1),\quad P(0,0,0).$

Jibu

$ z=0$

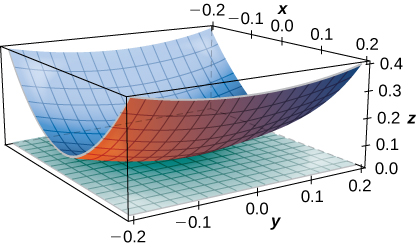
$Uso anayewakilisha kazi z=ln (10x ^ 2+2y ^ 2+1) na ndege yake tangent katika hatua (0, 0)$

52) [T] Kupata equation ya ndege tangent kwa uso$ z=f(x,y)=\sin(x+y^2)$ katika hatua$ \left(\frac{π}{4},0,\frac{\sqrt{2}}{2}\right)$, na grafu uso na ndege tangent.

Wachangiaji

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created all but part e of exercise 31.