14.5: Utawala wa Mlolongo wa Kazi nyingi

Malengo ya kujifunza

• Hali sheria mnyororo kwa vigezo moja au mbili huru.
• Tumia michoro za mti kama msaada wa kuelewa utawala wa mnyororo kwa vigezo kadhaa vya kujitegemea na vya kati.
• Kufanya tofauti thabiti ya kazi ya vigezo mbili au zaidi.

Katika calculus moja ya kutofautiana, tumegundua kuwa moja ya sheria muhimu zaidi za kutofautisha ni utawala wa mnyororo, ambayo inaruhusu sisi kupata derivative ya muundo wa kazi mbili. Kitu kimoja ni kweli kwa calculus multivariable, lakini wakati huu tunapaswa kukabiliana na aina zaidi ya moja ya utawala wa mnyororo. Katika sehemu hii, tunasoma upanuzi wa utawala wa mnyororo na kujifunza jinsi ya kuchukua derivatives ya nyimbo za kazi za kutofautiana zaidi ya moja.

Kanuni za Chain kwa Vigezo vya kujitegemea moja au mbili

Kumbuka kwamba utawala wa mnyororo kwa derivative ya composite ya kazi mbili inaweza kuandikwa kwa fomu

\[\dfrac{d}{dx}\Big(f(g(x))\Big)=f′\big(g(x)\big)g′(x). \nonumber \]

Katika equation hii, wote\(f(x)\) na\(g(x)\) ni kazi ya kutofautiana moja. Sasa tuseme kwamba\(f\) ni kazi ya vigezo mbili na\(g\) ni kazi ya variable moja. Au labda wao ni kazi zote mbili, au hata zaidi. Tunawezaje kuhesabu derivative katika kesi hizi? Theorem ifuatayo inatupa jibu kwa kesi ya kutofautiana moja ya kujitegemea.

Utawala wa Chain kwa Tofauti moja ya kujitegemea

Tuseme kwamba\(x=g(t)\) na\(y=h(t)\) ni differentiable kazi ya\(t\) na\(z=f(x,y)\) ni differentiable kazi ya\(x\) na\(y\). Kisha\(z=f(x(t),y(t))\) ni kazi differentiable ya\(t\) na

\[\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}, \label{chain1} \]

ambapo derivatives kawaida ni tathmini katika\(t\) na derivatives sehemu ni tathmini katika\((x,y)\).

Ushahidi

Ushahidi wa theorem hii inatumia ufafanuzi wa kutofautisha kazi ya vigezo viwili. Tuseme kwamba\(f\) ni differentiable katika hatua\(P(x_0,y_0),\) ambapo\(x_0=g(t_0)\) na\(y_0=h(t_0)\) kwa ajili ya thamani fasta ya\(t_0\). Tunataka kuthibitisha kwamba\(z=f\big(x(t),y(t)\big)\) ni tofauti katika\(t=t_0\) na kwamba Equation\ ref {Chain1} ana katika hatua hiyo pia.

Tangu\(f\) ni differentiable katika\(P\), tunajua kwamba

\[z(t)=f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \nonumber \]

wapi

\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \nonumber \]

Sisi kisha Ondoa\(z_0=f(x_0,y_0)\) kutoka pande zote mbili za equation hii:

\[ \begin{align*} z(t)−z(t_0) &=f(x(t),y(t))−f(x(t_0),y(t_0)) \\[4pt] &=f_x(x_0,y_0)(x(t)−x(t_0))+f_y(x_0,y_0)(y(t)−y(t_0))+E(x(t),y(t)). \end{align*}\]

Kisha, tunagawanya pande zote mbili kwa\(t−t_0\):

\[\frac{z(t)−z(t_0)}{t−t_0}=f_x(x_0,y_0)\frac{x(t)−x(t_0)}{t−t_0}+f_y(x_0,y_0)\frac{y(t)−y(t_0)}{t−t_0}+\frac{E(x(t),y(t))}{t−t_0}. \nonumber \]

Kisha sisi kuchukua kikomo kama\(t\) mbinu\(t_0\):

\[\begin{align*} \lim_{t→t_0}\dfrac{z(t)−z(t_0)}{t−t_0} &= f_x(x_0,y_0)\lim_{t→t_0} \left (\dfrac{x(t)−x(t_0)}{t−t_0} \right) \\[4pt] &+f_y(x_0,y_0)\lim_{t→t_0}\left (\dfrac{y(t)−y(t_0)}{t−t_0}\right)\\[4pt] &+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \end{align*}\]

Upande wa kushoto wa equation hii ni sawa na\(dz/dt\), ambayo inaongoza kwa

\[\dfrac{dz}{dt}=f_x(x_0,y_0)\dfrac{dx}{dt}+f_y(x_0,y_0)\dfrac{dy}{dt}+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \nonumber \]

Muda wa mwisho unaweza kuandikwa upya kama

\[\begin{align*} \lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0} &=\lim_{t→t_0}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}) \\[4pt] &=\lim_{t→t_0}\left(\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\right)\lim_{t→t_0}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \end{align*} \nonumber \]

Kama\(t\) mbinu\(t_0, \big(x(t),y(t)\big)\) mbinu\(\big(x(t_0),y(t_0)\big),\) ili tuweze kuandika upya bidhaa ya mwisho kama

\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\lim_{(x,y)→(x_0,y_0)}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \nonumber \]

Kwa kuwa kikomo cha kwanza ni sawa na sifuri, tunahitaji tu kuonyesha kwamba kikomo cha pili ni cha mwisho:

\[ \begin{align*} \lim_{(x,y)→(x_0,y_0)} \dfrac{\sqrt{ (x−x_0)^2+(y−y_0)^2 }} {t−t+0} =\lim_{(x,y)→(x_0,y_0)} \sqrt{ \dfrac { (x−x_0)^2+(y−y_0)^2 } {(t−t_0)^2} } \\[4pt] =\lim_{(x,y)→(x_0,y_0)}\sqrt{ \left(\dfrac{x−x_0}{t−t_0}\right)^2+\left(\dfrac{y−y_0}{t−t_0}\right)^2} \\[4pt] =\sqrt{ \left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{x−x_0}{t−t_0}\right)\right]^2+\left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{y−y_0}{t−t_0}\right)\right]^2}. \end{align*} \nonumber \]

Tangu\(x(t)\) na wote\(y(t)\) ni kazi differentiable ya\(t\), wote mipaka ndani radical mwisho kuwepo. Kwa hiyo, thamani hii ni ya mwisho. Hii inathibitisha utawala mnyororo katika\(t=t_0\); wengine wa theorem ifuatavyo kutokana na dhana kwamba kazi zote ni tofauti juu ya domains yao yote.

□

Uchunguzi wa karibu wa Equation\ ref {Chain1} unaonyesha muundo unaovutia. Muda wa kwanza katika equation ni\(\dfrac{∂f}{∂x} \cdot \dfrac{dx}{dt}\) na muda wa pili ni\(\dfrac{∂f}{∂y}⋅\dfrac{dy}{dt}\). Kumbuka kwamba wakati wa kuzidisha sehemu ndogo, kufuta kunaweza kutumika. Ikiwa tunachukua derivatives hizi kama sehemu ndogo, basi kila bidhaa “inafungua” kwa kitu kinachofanana\(∂f/dt\). Vigezo\(x\) na\(y\) kwamba kutoweka katika kurahisisha hii mara nyingi huitwa vigezo kati: wao ni vigezo huru kwa ajili ya kazi\(f\), lakini ni tegemezi vigezo kwa variable\(t\). Masharti mawili yanaonekana upande wa kulia wa formula, na\(f\) ni kazi ya vigezo viwili. Mfano huu kazi na kazi ya vigezo zaidi ya mbili kama vile, kama tunavyoona baadaye katika sehemu hii.

Mfano\(\PageIndex{1}\): Using the Chain Rule

Tumia\(dz/dt\) kwa kila kazi zifuatazo:

1. \(z=f(x,y)=4x^2+3y^2,\quad x=x(t)=\sin t,\quad y=y(t)=\cos t\)
2. \(z=f(x,y)=\sqrt{x^2−y^2},\quad x=x(t)=e^{2t},\quad y=y(t)=e^{−t}\)

Suluhisho

Kutumia utawala wa mnyororo, tunahitaji kiasi nne -\(∂z/∂x,\; ∂z/∂y, \; dx/dt\), na\(dy/dt\):

• \(\dfrac{∂z}{∂x}=8x\)
• \(\dfrac{dx}{dt}=\cos t\)
• \(\dfrac{∂z}{∂y}=6y\)
• \(\dfrac{dy}{dt}=−\sin t\)

Sasa, sisi badala ya kila moja ya haya katika Equation\ ref {Chain1}:

\ [kuanza {align*}\ dfrac {dz} {dt} &=\ dfrac {\ sehemu z} {\ sehemu x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ sehemu z} {\ sehemu y}\ cdot\ dfrac {dt}\\ [4pt]
& =( 8x) (\ cos t) + (6y) (-\ sin t)\\ [4pt]
&=8x\ cos t-6y\ sin t.\ mwisho {align*}\]

Jibu hili lina vigezo vitatu ndani yake. Kupunguza kwa variable moja, kutumia ukweli kwamba\(x(t)=\sin t\) na\(y(t)=\cos t.\) Sisi kupata

\ [kuanza {align*}\ dfrac {dz} {dt} &=8x\ cos t-6y\ sin t\\ [4pt]
&=8 (\ sin t)\ cos t-6 (\ cos t)\ sin t\\ [4pt]
&=2\ sin t\ cos t.\ mwisho {align*}\]

Derivative hii pia inaweza kuhesabiwa kwa kubadili kwanza\(x(t)\) na\(y(t)\)\(f(x,y),\) kisha kutofautisha kwa heshima na\(t\):

\ [kuanza {align*} z =f (x, y) &=f\ kubwa (x (t), y (t)\ kubwa)\\ [4pt]
&=4 (x (t)) ^2+3 (y (t)) ^2\\ [4pt]
&=4\ dhambi ^ 2 t+3\ cos ^ 2 t.\ mwisho {align*}\]

Kisha

\ [kuanza {align*}\ dfrac {dz} {dt} &=2 (4\ dhambi t) (\ cos t) +2 (3\ cos t) (-\ sin t)\\ [4pt]
&=8\ sin t\ cos t-6\ dhambi t\\ [4pt]
&=2\ sin t\ cos t,\ mwisho {align*}\]

ambayo ni ufumbuzi huo. Hata hivyo, inaweza kuwa si rahisi sana kutofautisha katika fomu hii.

b Kutumia utawala wa mnyororo, sisi tena tunahitaji kiasi nne -\(∂z/∂x,∂z/dy,dx/dt,\) na\(dy/dt:\)

• \(\dfrac{∂z}{∂x}=\dfrac{x}{\sqrt{x^2−y^2}}\)
• \(\dfrac{dx}{dt}=2e^{2t}\)
• \(\dfrac{∂z}{∂y}=\dfrac{−y}{\sqrt{x^2−y^2}}\)
• \(\dfrac{dx}{dt}=−e^{−t}.\)

Sisi badala ya kila moja ya hizi katika Equation\ ref {Chain1}:

\ [kuanza {align*}\ dfrac {dz} {dt} &=\ dfrac {\ sehemu z} {\ sehemu x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ sehemu z} {\ sehemu y}\ cdot\ dfrac {dt}\\ [4pt] &=\ kushoto (\ dfrac x {} {\ sqrt {x^2—y ^ 2}}\ haki) (2e^ {2t}) +\ kushoto (\ dfrac {-y} {\ sqrt {x^2,1y ^ 2}}\ haki) (-e ^ {18-t})\\ [4pt]
&=\ dfrac {2xe^ {2t}}\ sqrt {x^2,1y ^ 2}}. \ mwisho {align*}\ nonumber\]

Ili kupunguza hii kwa kutofautiana moja, tunatumia ukweli kwamba\(x(t)=e^{2t}\) na\(y(t)=e^{−t}\). Kwa hiyo,

\ [kuanza {align*}\ dfrac {dz} {dt} &=\ dfrac {2xe^2t+ye^ {-t}} {\ sqrt {x^2,1y ^ 2}}\\ [4pt]
&=\ dfrac {2 (e ^ {2t}) e^ {e^ {t}}} {\ sqrt {e^ {4t} -e ^ {-2t}}}\\ [4pt]
&=\ dfrac {2e ^ {4t} +e ^ {-2t}} {\ sqrt {e^ {4t}}}}. \ mwisho {align*}\ nonumber\]

Ili kuondokana na vielelezo hasi, tunazidisha juu\(e^{2t}\) na chini na\(\sqrt{e^{4t}}\):

\ [kuanza {align*}\ dfrac {dz} {dt} &=\ dfrac {2e ^ {4t} +e ^ {-2t}} {\ sqrt {e^ {4t}}} {-2t}}}} {e^ {2t} {e^ {4t}}\\ [4pt]
&=\ dfrac {2e ^ {6t} +1} {\ sqrt {8t} -e ^ {2t}}}\\ [4pt]
&=\ dfrac {2e} {6t} +1} {\ sqrt {e ^ {2t} (e ^ {6t} -1)}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {e ^ t\ sqrt {e^ {6t} -1}}. \ mwisho {align*}\]

Tena, derivative hii pia inaweza kuhesabiwa kwa kubadili kwanza\(x(t)\) na\(y(t)\)\(f(x,y),\) kisha kutofautisha kwa heshima na\(t\):

\[\begin{align*} z &=f(x,y) \\[4pt] &=f(x(t),y(t)) \\[4pt] &=\sqrt{(x(t))^2−(y(t))^2} \\[4pt] &=\sqrt{e^{4t}−e^{−2t}} \\[4pt] &=(e^{4t}−e^{−2t})^{1/2}. \end{align*} \nonumber \]

Kisha

\[ \begin{align*} \dfrac{dz}{dt} &= \dfrac{1}{2} (e^{4t}−e^{−2t})^{−1/2} \left(4e^{4t}+2e^{−2t} \right) \\[4pt] &=\dfrac{2e^{4t}+e^{−2t}}{\sqrt{e^{4t}−e^{−2t}}}. \end{align*}\]

Hii ni suluhisho sawa.

Zoezi\(\PageIndex{1}\)

\(dz/dt \)Tumia kazi zifuatazo. Eleza jibu la mwisho katika suala la\(t\).

\[ \begin{align*} z =f(x,y) &=x^2−3xy+2y^2,\\[4pt] x =x(t) &=3\sin 2t,\\[4pt] y=y(t) &=4\cos 2t \end{align*}\]

Kidokezo

Tumia\(∂z/∂x,∂z/dy,dx/dt,\) na\(dy/dt\), kisha utumie Equation\ ref {Chain1}.

Jibu

\ (kuanza {align*}\ dfrac {dz} {dz} &=\ dfrac {f} {x}\ dfrac {x} {dx} {dt} +\ dfrac {y}\ dfrac {y}\ dfrac {dt}\ [5pt]
& =( 2x-3y) (6\ cos 2t) + (-3x3x+4y) (-8\ dhambi 2t)\\ [5pt]
&=—92\ dhambi 2t\ cos 2t-72 (\ cos ^22-\ dhambi ^ 2 2t)\\ [5pt]
&=-46\ dhambi 4t-72\ cos 4t. \ mwisho {align*}\)

Mara nyingi ni muhimu kuunda uwakilishi wa kuona wa Equation\ ref {Chain1} kwa utawala wa mnyororo. Hii inaitwa mchoro wa mti kwa utawala wa mnyororo kwa kazi za kutofautiana moja na hutoa njia ya kukumbuka formula (Kielelezo\(\PageIndex{1}\)). Mchoro huu unaweza kupanuliwa kwa kazi za kutofautiana zaidi ya moja, kama tutakavyoona muda mfupi sana.

Kielelezo\(\PageIndex{1}\): Mchoro wa mti kwa kesi hiyo\(\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}.\)

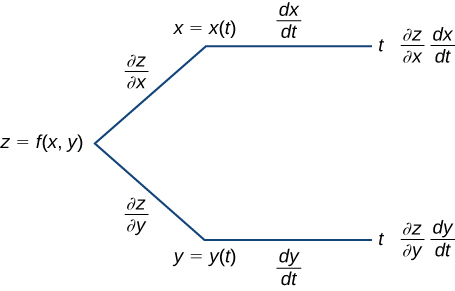
Katika mchoro huu, kona ya kushoto inafanana na\(z=f(x,y)\). Kwa kuwa\(f\) ina vigezo viwili vya kujitegemea, kuna mistari miwili inayotoka kona hii. Tawi la juu linalingana na variable\(x\) na tawi la chini linalingana na variable\(y\). Kwa kuwa kila moja ya vigezo hivi ni tegemezi kwa variable moja\(t\), tawi moja kisha linatokana\(x\) na tawi moja linatokana na\(y\). Mwisho, kila matawi upande wa kulia wa mbali ana lebo inayowakilisha njia iliyosafiri kufikia tawi hilo. Tawi la juu linafikiwa kwa kufuata\(x\) tawi, kisha tawi la t; kwa hiyo, ni lebo Tawi\((∂z/∂x)×(dx/dt).\) la chini ni sawa: kwanza\(y\) tawi, kisha\(t\) tawi. Tawi hili limeandikwa\((∂z/∂y)×(dy/dt)\). Ili kupata formula kwa\(dz/dt,\) kuongeza maneno yote yanayotokea upande wa kulia wa mchoro. Hii inatupa Equation.

Katika Kumbuka,\(z=f(x,y)\) ni kazi ya\(x\) na\(y\), na wote wawili\(x=g(u,v)\) na\(y=h(u,v)\) ni kazi ya vigezo huru\(u\) na\(v\).

Utawala wa Chain kwa vigezo viwili vya kujitegemea

Tuseme\(x=g(u,v)\) na\(y=h(u,v)\) ni differentiable kazi ya\(u\) na\(v\), na\(z=f(x,y)\) ni kazi differentiable ya\(x\) na\(y\). Kisha,\(z=f(g(u,v),h(u,v))\) ni kazi differentiable ya\(u\) na\(v\), na

\[\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂u} \label{chain2a} \]

na

\[\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v}. \label{chain2b} \]

Tunaweza kuteka mchoro wa mti kwa kila moja ya kanuni hizi kama ifuatavyo.

Kielelezo\(\PageIndex{2}\): Mchoro wa mti kwa\(\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}\) na\(\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}\).

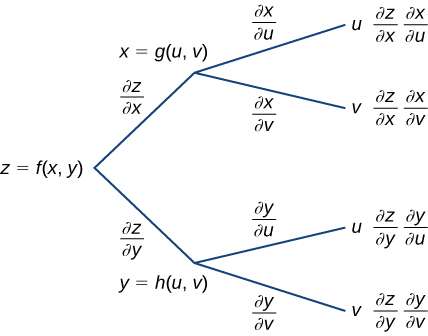
Ili kupata formula kwa\(∂z/∂u\), kuanza kutoka upande wa kushoto wa mchoro, kisha ufuate matawi tu yanayomaliza\(u\) na kuongeza maneno yanayotokea mwishoni mwa matawi hayo. Kwa formula kwa\(∂z/∂v\), kufuata tu matawi kwamba mwisho\(v\) na na kuongeza maneno kwamba kuonekana katika mwisho wa matawi hayo.

Kuna tofauti muhimu kati ya theorems hizi mbili za utawala wa mnyororo. Katika Kumbuka, upande wa kushoto wa formula kwa derivative sio derivative sehemu, lakini katika Kumbuka ni. Sababu ni kwamba, katika Kumbuka, hatimaye\(z\) ni kazi ya\(t\) peke yake, wakati katika Kumbuka,\(z\) ni kazi ya wote\(u\) na\(v\).

Mfano\(\PageIndex{2}\): Using the Chain Rule for Two Variables

Tumia\(∂z/∂u\) na\(∂z/∂v\) kutumia kazi zifuatazo:

\[z=f(x,y)=3x^2−2xy+y^2,\; x=x(u,v)=3u+2v,\; y=y(u,v)=4u−v. \nonumber \]

Suluhisho

Ili kutekeleza utawala wa mnyororo kwa vigezo viwili, tunahitaji derivatives sita sehemu -\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\) na\(∂y/∂v\):

\[\begin{align*} \dfrac{∂z}{∂x} &=6x−2y & & \dfrac{∂z}{∂y}=−2x+2y \\[4pt] \dfrac{∂x}{∂u} &=3 & & \dfrac{∂x}{∂v}=2 \\[4pt] \dfrac{∂y}{∂u} &=4 & & \dfrac{∂y}{∂v}=−1. \end{align*}\]

Ili kupata\(∂z/∂u,\) tunatumia Equation\ ref {Chain2a}:

\ [kuanza {align*}\ dfrac {z} {u} &=\ dfrac {z} {x}}\ dfrac {x} {u} +\ dfrac {y} {y} {y} {y} {u}\ [4pt]
&=3 (6x-2y) +4 (-2y x+2y)\\ [4pt]
&= 10x+2y. \ mwisho {align*}\]

Kisha, sisi badala\(x(u,v)=3u+2v\) na\(y(u,v)=4u−v:\)

\[\begin{align*} \dfrac{∂z}{∂u} &=10x+2y \\[4pt] &=10(3u+2v)+2(4u−v) \\[4pt] &=38u+18v. \end{align*}\]

Ili kupata\(∂z/∂v,\) tunatumia Equation\ ref {Chain2b}:

\[\begin{align*} \dfrac{∂z}{∂v} &=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v} \\[4pt] &=2(6x−2y)+(−1)(−2x+2y) \\[4pt] &=14x−6y. \end{align*}\]

Kisha sisi badala\(x(u,v)=3u+2v\) na\(y(u,v)=4u−v:\)

\[\begin{align*} \dfrac{∂z}{∂v} &=14x−6y \\[4pt] &=14(3u+2v)−6(4u−v) \\[4pt] &=18u+34v \end{align*}\]

Zoezi\(\PageIndex{2}\)

Tumia\(∂z/∂u\) na\(∂z/∂v\) kupewa kazi zifuatazo:

\[ z=f(x,y)=\dfrac{2x−y}{x+3y},\quad x(u,v)=e^{2u}\cos 3v,\quad y(u,v)=e^{2u}\sin 3v. \nonumber \]

Kidokezo

Tumia hesabu\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\) na\(∂y/∂v\), kisha utumie Equation\ ref {Chain2a} na Equation\ ref {Chain2b}.

Jibu

\(\dfrac{∂z}{∂u}=0,\quad \dfrac{∂z}{∂v}=\dfrac{−21}{(3\sin 3v+\cos 3v)^2}\)

Utawala wa Mlolongo

Sasa kwa kuwa tumeona jinsi ya kupanua awali mlolongo utawala kwa kazi ya vigezo mbili, ni kawaida kuuliza: Je, tunaweza kupanua utawala kwa vigezo zaidi ya mbili? Jibu ni ndiyo, kama utawala wa mnyororo wa jumla unasema.

Utawala wa Chain wa jumla

Hebu\(w=f(x_1,x_2,…,x_m)\) kuwa kazi tofauti ya vigezo vya\(m\) kujitegemea, na kwa kila\(i∈{1,…,m},\) basi\(x_i=x_i(t_1,t_2,…,t_n)\) iwe kazi tofauti ya vigezo vya\(n\) kujitegemea. Kisha

\[\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_2}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j} \nonumber \]

kwa yoyote\(j∈{1,2,…,n}.\)

Katika mfano unaofuata sisi mahesabu derivative ya kazi ya vigezo tatu kujitegemea ambayo kila moja ya vigezo tatu ni tegemezi kwa vigezo vingine viwili.

Mfano\(\PageIndex{3}\): Using the Generalized Chain Rule

Tumia\(∂w/∂u\) na\(∂w/∂v\) kutumia kazi zifuatazo:

\[\begin{align*} w &=f(x,y,z)=3x^2−2xy+4z^2 \\[4pt] x &=x(u,v)=e^u\sin v \\[4pt] y &=y(u,v)=e^u\cos v \\[4pt] z &=z(u,v)=e^u. \end{align*}\]

Suluhisho

Fomu kwa\(∂w/∂u\) na\(∂w/∂v\) ni

\[\begin{align*} \dfrac{∂w}{∂u} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v}. \end{align*}\]

Kwa hiyo, kuna derivatives tisa tofauti ambazo zinahitaji kuhesabiwa na kubadilishwa. Tunahitaji kuhesabu kila mmoja wao:

\[\begin{align*} \dfrac{∂w}{∂x}&=6x−2y \dfrac{∂w}{∂y}=−2x \dfrac{∂w}{∂z}=8z \\[4pt] \dfrac{∂x}{∂u}&=e^u\sin v \dfrac{∂y}{∂u}=e^u\cos v \dfrac{∂z}{∂u}=e^u \\[4pt] \dfrac{∂x}{∂v}&=e^u\cos v \dfrac{∂y}{∂v}=−e^u\sin v \dfrac{∂z}{∂v}=0. \end{align*}\]

Sasa, sisi badala ya kila mmoja wao katika formula ya kwanza ya kuhesabu\( ∂w/∂u\):

\ [kuanza {align*}\ dfrac {w} {u} &=\ dfrac {w} {x}}\ dfrac {x} {u} +\ dfrac {w} {y} {y} {y} {y} {u} {z}\ dfrac {z} {z}\ dfrac {z} {z} {z}} {u}\\ [4pt]
& =( 6x-2y) e ^ u\ dhambi v-2xe^u\ cos v+8ze ^ u,\ mwisho {align*}\]

kisha mbadala\(x(u,v)=e^u \sin v, \, y(u,v)=e^u\cos v,\) na\(z(u,v)=e^u\) katika equation hii:

\[\begin{align*} \dfrac{∂w}{∂u} &=(6x−2y)e^u\sin v−2xe^u\cos v+8ze^u \\[4pt] &=(6e^u\sin v−2eu\cos v)e^u\sin v−2(e^u\sin v)e^u\cos v+8e^{2u} \\[4pt] &=6e^{2u}\sin^2 v−4e^{2u}\sin v\cos v+8e^{2u} \\[4pt] &=2e^{2u}(3\sin^2 v−2\sin v\cos v+4). \end{align*}\]

Kisha, tunahesabu\(∂w/∂v\):

\[\begin{align*} \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v} \\[4pt] &=(6x−2y)e^u\cos v−2x(−e^u\sin v)+8z(0), \end{align*}\]

basi sisi badala\(x(u,v)=e^u\sin v,\, y(u,v)=e^u\cos v,\) na\(z(u,v)=e^u\) katika equation hii:

\[\begin{align*} \dfrac{∂w}{∂v} &=(6x−2y)e^u\cos v−2x(−e^u\sin v) \\[4pt] &=(6e^u \sin v−2e^u\cos v)e^u\cos v+2(e^u\sin v)(e^u\sin v) \\[4pt] &=2e^{2u}\sin^2 v+6e^{2u}\sin v\cos v−2e^{2u}\cos^2 v \\[4pt] &=2e^{2u}(\sin^2 v+\sin v\cos v−\cos^2 v). \end{align*}\]

Zoezi\(\PageIndex{3}\)

Tumia\(∂w/∂u\) na\(∂w/∂v\) kupewa kazi zifuatazo:

\[\begin{align*} w &=f(x,y,z)=\dfrac{x+2y−4z}{2x−y+3z} \\[4pt] x &=x(u,v)=e^{2u}\cos3v \\[4pt] y &=y(u,v)=e^{2u}\sin 3v \\[4pt] z &=z(u,v)=e^{2u}. \end{align*}\]

Kidokezo

Tumia derivatives ya sehemu tisa, kisha utumie fomu sawa kutoka kwa Mfano\(\PageIndex{3}\).

Jibu

\(\dfrac{∂w}{∂u}=0\)

\(\dfrac{∂w}{∂v}=\dfrac{15−33\sin 3v+6\cos 3v}{(3+2\cos 3v−\sin 3v)^2}\)

Mfano\(\PageIndex{4}\): Drawing a Tree Diagram

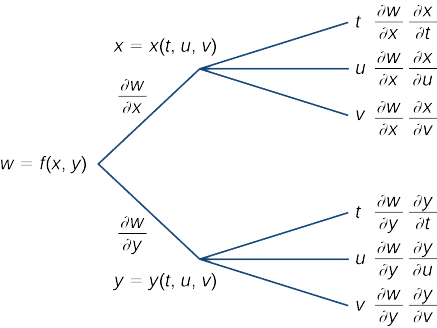
Unda mchoro wa mti kwa kesi wakati

\[ w=f(x,y,z),\quad x=x(t,u,v),\quad y=y(t,u,v),\quad z=z(t,u,v) \nonumber \]

na kuandika formula kwa ajili ya derivatives tatu sehemu ya\(w\).

Suluhisho

Kuanzia upande wa kushoto, kazi\(f\) ina vigezo vitatu vya kujitegemea:\(x,\, y\), na\(z\). Kwa hiyo, matawi matatu yanapaswa kuwa kutoka kwa node ya kwanza. Kila moja ya matawi haya matatu pia ina matawi matatu, kwa kila moja ya vigezo\(t,\, u,\) na\(v\).

Kielelezo\(\PageIndex{3}\): Mti mchoro kwa ajili ya kazi ya vigezo tatu, ambayo kila ni kazi ya vigezo tatu huru.

Fomula tatu ni

\[\begin{align*} \dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂v}. \end{align*}\]

Zoezi\(\PageIndex{4}\)

Unda mchoro wa mti kwa kesi wakati

\[w=f(x,y),\quad x=x(t,u,v),\quad y=y(t,u,v) \nonumber \]

na kuandika formula kwa ajili ya derivatives tatu sehemu ya\(w.\)

Kidokezo

Kuamua idadi ya matawi yanayotokana na kila node katika mti.

Jibu

\[\begin{align*}\dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v} \end{align*}\]

Tofauti thabiti

Kumbuka kutoka upambanuzi thabiti hutoa njia kwa ajili ya kutafuta\(dy/dx\) wakati\(y\) hufafanuliwa kimsingi kama kazi ya\(x\). Njia hii inahusisha kutofautisha pande zote mbili za equation inayofafanua kazi kwa heshima na\(x\), kisha kutatua kwa derivatives ya\(dy/dx.\) sehemu hutoa mbadala kwa njia hii.

Fikiria duaradufu inavyoelezwa na equation\(x^2+3y^2+4y−4=0\) kama ifuatavyo.

Kielelezo\(\PageIndex{4}\): Grafu ya duaradufu inavyoelezwa na\(x^2+3y^2+4y−4=0\).

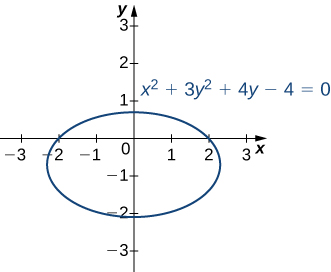
Equation hii inamweka amefafanua\(y\) kama kazi ya\(x\). Kwa hivyo, tunaweza kupata derivative\(dy/dx\) kwa kutumia njia ya kutofautisha thabiti:

\[\begin{align*} \dfrac{d}{dx}(x^2+3y^2+4y−4) &=\dfrac{d}{dx}(0) \\[4pt] 2x+6y\dfrac{dy}{dx}+4\dfrac{dy}{dx} &=0 \\[4pt] (6y+4)\dfrac{dy}{dx} &=−2x\\[4pt] \dfrac{dy}{dx} &=−\dfrac{x}{3y+2}\end{align*}\]

Tunaweza pia kufafanua kazi\(z=f(x,y)\) kwa kutumia upande wa kushoto wa equation kufafanua duaradufu. Kisha\(f(x,y)=x^2+3y^2+4y−4.\) duaradufu\(x^2+3y^2+4y−4=0\) inaweza kisha kuelezewa na equation\(f(x,y)=0\). Kutumia kazi hii na theorem ifuatayo inatupa njia mbadala ya kuhesabu\(dy/dx.\)

Theorem: Tofauti thabiti ya Kazi ya Vigezo Mbili au Zaidi

Tuseme kazi\(z=f(x,y)\)\(y\) amefafanua inamaanisha kama kazi\(y=g(x)\) ya\(x\) kupitia equation\(f(x,y)=0.\) Kisha

\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y} \label{implicitdiff1} \]

zinazotolewa\(f_y(x,y)≠0.\)

Kama equation\(f(x,y,z)=0\)\(z\) amefafanua inamweka kama kazi differentiable ya\(x\) na\(y\), basi

\[\dfrac{dz}{dx}=−\dfrac{∂f/∂x}{∂f/∂z} \qquad\text{and}\qquad \dfrac{dz}{dy}=−\dfrac{∂f/∂y}{∂f/∂z}\label{implicitdiff2} \]

kwa muda mrefu kama\(f_z(x,y,z)≠0.\)

Equation\ ref {implicitdiff1} ni matokeo ya moja kwa moja ya Equation\ ref {Chain2a}. Hasa, kama sisi kudhani kwamba\(y\) ni defined inamaanisha kama kazi ya\(x\) kupitia equation\(f(x,y)=0\), tunaweza kutumia utawala mnyororo kupata\(dy/dx:\)

\[\begin{align*} \dfrac{d}{dx}f(x,y) &=\dfrac{d}{dx}(0) \\[4pt] \dfrac{∂f}{∂x}⋅\dfrac{dx}{dx}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0 \\[4pt]\dfrac{∂f}{∂x}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0. \end{align*}\]

Kutatua equation hii kwa\(dy/dx\) anatoa Equation\ ref {implicitdiff1}. Equation\ ref {implicitdiff1} inaweza inayotokana kwa mtindo sawa.

Hebu sasa kurudi tatizo ambalo tulianza kabla ya theorem ya awali. Kutumia Kumbuka na kazi\(f(x,y)=x^2+3y^2+4y−4,\) tunayopata

\[\begin{align*} \dfrac{∂f}{∂x} &=2x\\[4pt] \dfrac{∂f}{∂y} &=6y+4. \end{align*}\]

Kisha Equation\ ref {implicitdiff1} anatoa

\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=−\dfrac{2x}{6y+4}=−\dfrac{x}{3y+2}, \nonumber \]

ambayo ni matokeo sawa kupatikana kwa matumizi ya awali ya upambanuzi thabiti.

Mfano\(\PageIndex{5}\): Implicit Differentiation by Partial Derivatives

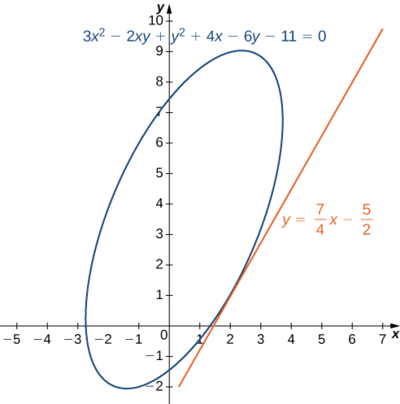
1. Mahesabu\(dy/dx\) kama\(y\) hufafanuliwa inamaanisha kama kazi ya\(x\) kupitia equation\(3x^2−2xy+y^2+4x−6y−11=0\). Nini equation ya mstari tangent kwa grafu ya Curve hii katika hatua\((2,1)\)?
2. Tumia\(∂z/∂x\) na\(∂z/∂y,\) kupewa\(x^2e^y−yze^x=0.\)

Suluhisho

a Weka\(f(x,y)=3x^2−2xy+y^2+4x−6y−11=0,\) kisha uhesabu\(f_x\) na\(f_y: f_x(x,y)=6x−2y+4\) na\(f_y(x,y)=−2x+2y−6.\)

Derivative hutolewa na

\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=\dfrac{6x−2y+4}{−2x+2y−6}=\dfrac{3x−y+2}{x−y+3}. \nonumber \]

Mteremko wa mstari wa tangent katika hatua\((2,1)\) hutolewa na

\[\dfrac{dy}{dx}\Bigg|_{(x,y)=(2,1)}=\dfrac{3(2)−1+2}{2−1+3}=\dfrac{7}{4} \nonumber \]

Ili kupata usawa wa mstari wa tangent, tunatumia fomu ya mteremko wa uhakika (Kielelezo\(\PageIndex{5}\)):

\[\begin{align*} y−y_0 &=m(x−x_0)\\[4pt]y−1 &=\dfrac{7}{4}(x−2) \\[4pt] y &=\dfrac{7}{4}x−\dfrac{7}{2}+1\\[4pt] y &=\dfrac{7}{4}x−\dfrac{5}{2}.\end{align*}\]

Kielelezo\(\PageIndex{5}\): Grafu ya duaradufu kuzungushwa inavyoelezwa na\(3x^2−2xy+y^2+4x−6y−11=0\).

b Tuna\(f(x,y,z)=x^2e^y−yze^x.\) Kwa hiyo,

\[\begin{align*} \dfrac{∂f}{∂x} &=2xe^y−yze^x \\[4pt] \dfrac{∂f}{∂y} &=x^2e^y−ze^x \\[4pt] \dfrac{∂f}{∂z} &=−ye^x\end{align*}\]

Kutumia Equation\ ref {implicitdiff2},

\[\begin{align*} \dfrac{∂z}{∂x} &=−\dfrac{∂f/∂x}{∂f/∂y} & &\text{and} & \dfrac{∂z}{∂y} =−\dfrac{∂f/∂y}{∂f/∂z} \\[4pt] &=−\dfrac{2xe^y−yze^x}{−ye^x} & & &=−\dfrac{x^2e^y−ze^x}{−ye^x} \\[4pt] &=\dfrac{2xe^y−yze^x}{ye^x} & & & =\dfrac{x^2e^y−ze^x}{ye^x} \end{align*}\]

Zoezi\(\PageIndex{5}\)

Kupata\(dy/dx\) kama\(y\) hufafanuliwa inamaanisha kama kazi ya\(x\) kwa equation\(x^2+xy−y^2+7x−3y−26=0\). Nini equation ya mstari tangent kwa grafu ya Curve hii katika hatua\((3,−2)\)?

Kidokezo

Tumia\(∂f/dx\) na\(∂f/dy\), kisha utumie Equation\ ref {implicitdiff1}.

Suluhisho

\[\dfrac { d y } { d x } = \left. \frac { 2 x + y + 7 } { 2 y - x + 3 } \right| _ { ( 3 , - 2 ) } = \dfrac { 2 ( 3 ) + ( - 2 ) + 7 } { 2 ( - 2 ) - ( 3 ) + 3 } = - \dfrac { 11 } { 4 } \nonumber \]

Ulinganisho wa mstari wa tangent:\(y=−\dfrac{11}{4}x+\dfrac{25}{4}\)

Dhana muhimu

• Utawala wa mnyororo wa kazi za kutofautiana zaidi ya moja unahusisha derivatives ya sehemu kwa heshima na vigezo vyote vya kujitegemea.
• Miti michoro ni muhimu kwa ajili ya kupata formula kwa utawala mnyororo kwa ajili ya kazi ya variable zaidi ya moja, ambapo kila variable kujitegemea pia inategemea vigezo vingine.

Mlinganyo muhimu

• Chain utawala, moja ya kujitegemea variable

\(\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}\)

• Utawala wa mlolongo, vigezo viwili vya kujitegemea

\(\dfrac{dz}{du}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}\dfrac{dz}{dv}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}\)

• Utawala wa mzunguko wa jumla

\(\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_1}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j}\)

faharasa

utawala wa mnyororo wa jumla

utawala wa mnyororo uliongezwa kwa kazi za variable zaidi ya moja ya kujitegemea, ambayo kila variable huru inaweza kutegemea vigezo vingine au zaidi

variable kati

kutokana na muundo wa kazi (kwa mfano\(f(x(t),y(t)))\), vigezo kati ni vigezo ambavyo ni huru katika kazi ya nje lakini hutegemea vigezo vingine pia; katika kazi\(f(x(t),y(t)),\) vigezo\(x\) na\(y\) ni mifano ya vigezo vya kati

mchoro wa mti

inaonyesha na hupata fomu kwa utawala wa mnyororo wa jumla, ambapo kila kutofautiana kwa kujitegemea huhesabiwa