Skip to main content
Global

13.3E: Mazoezi ya Sehemu ya 13.3

  1. Last updated
  2. Save as PDF
  • Page ID
    178292

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Kuamua Urefu wa Arc

    Katika maswali 1 - 5, tafuta urefu wa arc wa safu kwenye muda uliopewa.

    1)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+(2t^2+1)\,\hat{\mathbf{j}}, \quad 1≤t≤3\)

    Jibu
    \(8\sqrt{5}\)vitengo

    2)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+14t \,\hat{\mathbf{j}},\quad 0≤t≤7\). Sehemu hii ya grafu imeonyeshwa hapa:

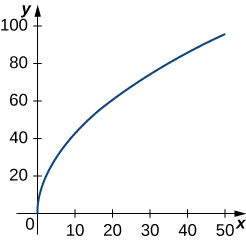
    3)\(\vecs r(t)=⟨t^2+1,4t^3+3⟩, \quad −1≤t≤0\)

    Jibu
    \(\frac{1}{54}(37^{3/2}−1)\)vitengo

    4)\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩,\quad 0≤t≤π\). Sehemu hii ya grafu imeonyeshwa hapa:

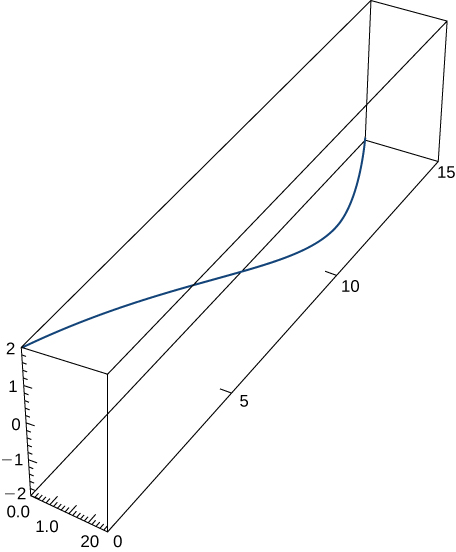
    5)\(\vecs r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩\) zaidi ya muda\([0,\frac{π}{2}]\). Hapa ni sehemu ya grafu kwenye muda ulioonyeshwa:

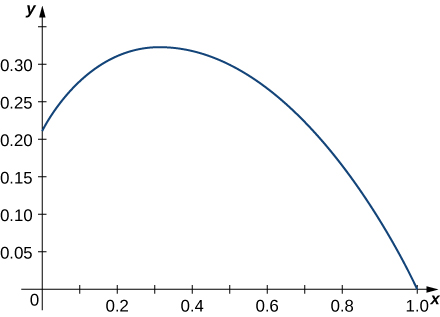
    6) Weka muhimu ili kuwakilisha urefu wa arc kutoka\(t = 0\) kwa\(t = 2\) kando ya pembe iliyofuatiliwa na\(\vecs r(t) = \langle t, \, t^4\rangle.\) Kisha utumie teknolojia ili kufikia urefu huu kwa karibu elfu ya kitengo.

    7) Pata urefu wa upande mmoja wa helix iliyotolewa na\(\vecs r(t)= \frac{1}{2} \cos t \,\hat{\mathbf{i}}+\frac{1}{2} \sin t \,\hat{\mathbf{j}}+\frac{\sqrt{3}}{2}\,t \,\hat{\mathbf{k}}\).

    Jibu
    Urefu\(=2π\) vitengo

    8) Pata urefu wa arc wa kazi yenye thamani ya vector\(\vecs r(t)=−t \,\hat{\mathbf{i}}+4t \,\hat{\mathbf{j}}+3t \,\hat{\mathbf{k}}\) juu\([0,1]\).

    9) chembe husafiri katika mduara na equation ya mwendo\(\vecs r(t)=3 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}} +0 \,\hat{\mathbf{k}}\). Pata umbali uliosafiri kuzunguka mduara na chembe.

    Jibu
    \(6π\)vitengo

    10) Weka muhimu ili kupata mzunguko wa ellipse na equation\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\).

    11) Pata urefu wa curve\(\vecs r(t)=⟨\sqrt{2}t,\, e^t, \, e^{−t}⟩\) juu ya muda\(0≤t≤1\). Grafu inavyoonyeshwa hapa:

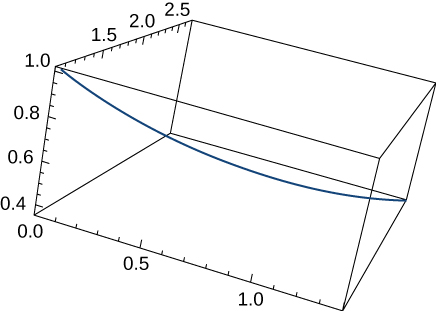
    Jibu
    \(\left(e−\frac{1}{e}\right)\)vitengo

    12) Kupata urefu wa Curve\(\vecs r(t)=⟨2 \sin t, \, 5t, \, 2 \cos t⟩\) kwa\(t∈[−10,10]\).

    Kitengo cha Tangent Vectors na Vectors Kitengo cha kawaida

    13) Kazi ya msimamo kwa chembe ni\(\vecs r(t)=a \cos( ωt) \,\hat{\mathbf{i}}+b \sin (ωt) \,\hat{\mathbf{j}}\). Kupata kitengo tangent vector na kitengo vector kawaida katika\(t=0\).

    Suluhisho:
    \ (\ kuanza {align*}\ vecs r' (t) &= -aΩ\ dhambi (ωt)\,\ kofia {\ mathbf {i}} +bΩ\ cos (ωt)\,\ kofia {\ mathbf {j}}\\ [5pt]
    \ |\ vecs r' (t)\ | &=\ sqrt {a^2 ω^2\ dhambi ^ 2 (ωt) +b ^ 2ω^2\ cos^2 (ωt)}\\ [5pt]
    \ vecs T (t) &=\ dfrac {\ vecs r' (t)} {\ |\ vecs r' (t)\ |} =\ dfrac {-aΩ\ dhambi (ωt)\,\ kofia {\ mathbf {i}} +bΩ\ cos (ωt)\,\ kofia {\ mathbf {j}}} {\ sqrt {a^2 ω^2\ sin^2 (ωt) +b ^ 2ω^2\ cos^2 (ωt)}}\\ [5pt]
    \ vecs T (0) &=\ dfrac {bΩ\,\ kofia {\ mathbf {j}}} {\ sqrt {(bΩ) ^2}} =\ dfrac {bω\,\ kofia {\ mathbf {j}}} {|bω|}\ mwisho {align*}\)

    Kama\(bω > 0, \; \vecs T(0) = \hat{\mathbf{j}},\) na kama\( bω < 0, \; T(0)= -\hat{\mathbf{j}}\)
    Jibu
    Kama\(bω > 0, \; \vecs T(0)= \hat{\mathbf{j}},\) na kama\( bω < 0, \; \vecs T(0)= -\hat{\mathbf{j}}\)

    kama\(a > 0, \; \vecs N(0)= -\hat{\mathbf{i}},\) na kama\( a < 0, \; \vecs N(0)= \hat{\mathbf{i}}\)

    14) Kutokana\(\vecs r(t)=a \cos (ωt) \,\hat{\mathbf{i}} +b \sin (ωt) \,\hat{\mathbf{j}}\), kupata vector binormal\(\vecs B(0)\).

    15) Kutokana\(\vecs r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩\), kuamua kitengo tangent vector\(\vecs T(t)\).

    Jibu
    \ (\ kuanza {align*}\ vecs T (t) &=\ kushoto\ langle\ frac {2} {\ sqrt {6}},\ frac {\ cos t-|sin t} {\ sqrt {6}},\,\ frac {\ cos t+\ sin t} {\ sqrt {6}}\ haki\ rangle\\ [4pt]
    &=\ kushoto\ angle\ frac {\ sqrt {6}} {3},\,\ frac {\ sqrt {6}} {6} (\ cos t-\ sin t),\,\ frac {\ sqrt {6}} {6} (\ cos t+\ dhambi t)\ haki\ rangle\ mwisho { align*}\)

    16) Kutokana\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), kupata kitengo tangent vector\(\vecs T(t)\) tathmini katika\(t=0\),\(\vecs T(0)\).

    17) Kutokana\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), kuamua kitengo vector kawaida\(\vecs N(t)\).

    Jibu
    \(\vecs N(t)=⟨0,\, -\frac{\sqrt{2}}{2} (\sin t + \cos t), \, \frac{\sqrt{2}}{2} (\cos t- \sin t)⟩\)

    18) kutokana\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), kupata kitengo vector kawaida\(\vecs N(t)\) tathmini katika\(t=0\),\(\vecs N(0)\).

    Jibu
    \(\vecs N(0)=⟨0, \;-\frac{\sqrt{2}}{2},\;\frac{\sqrt{2}}{2}⟩\)

    19) Kutokana\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), kupata kitengo tangent vector\(\vecs T(t)\). Grafu inavyoonyeshwa hapa:

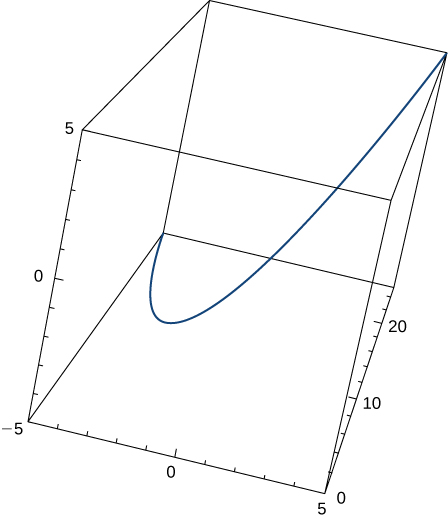
    Jibu
    \(\vecs T(t)=\dfrac{1}{\sqrt{4t^2+2}}<1,2t,1>\)

    20) Kupata kitengo tangent vector\(\vecs T(t)\) na kitengo kawaida vector\(\vecs N(t)\) saa\(t=0\) kwa Curve ndege\(\vecs r(t)=⟨t^3−4t,5t^2−2⟩\). Grafu inavyoonyeshwa hapa:

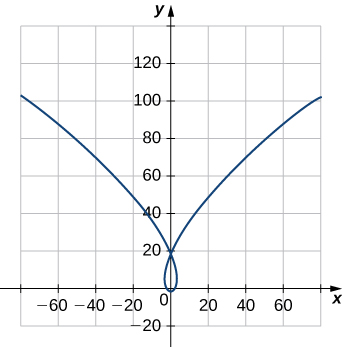
    21) Kupata kitengo tangent vector\(\vecs T(t)\) kwa\(\vecs r(t)=3t \,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}+2t \,\hat{\mathbf{k}}\).

    Jibu
    \(\vecs T(t)=\dfrac{1}{\sqrt{100t^2+13}}(3 \,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}})\)

    22) Kupata kuu ya kawaida vector kwa Curve\(\vecs r(t)=⟨6 \cos t,6 \sin t⟩\) katika hatua kuamua na\(t=\frac{π}{3}\).

    23) Kupata\(\vecs T(t)\) kwa Curve\(\vecs r(t)=(t^3−4t) \,\hat{\mathbf{i}}+(5t^2−2) \,\hat{\mathbf{j}}\).

    Jibu
    \(\vecs T(t)=\dfrac{1}{\sqrt{9t^4+76t^2+16}}\big((3t^2−4)\,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}\big)\)

    24) Kupata\(\vecs N(t)\) kwa Curve\(\vecs r(t)=(t^3−4t)\,\hat{\mathbf{i}}+(5t^2−2)\,\hat{\mathbf{j}}\).

    25) Kupata kitengo tangent vector\(\vecs T(t)\) kwa\(\vecs r(t)=⟨2 \sin t,\, 5t,\, 2 \cos t⟩\).

    Jibu
    \(\vecs T(t)=⟨\frac{2\sqrt{29}}{29}\cos t,\, \frac{5\sqrt{29}}{29},\,−\frac{2\sqrt{29}}{29}\sin t⟩\)

    26) Kupata kitengo vector kawaida\(\vecs N(t)\) kwa\(\vecs r(t)=⟨2\sin t,\,5t,\,2\cos t⟩\).

    Jibu
    \(\vecs N(t)=⟨−\sin t,\, 0,\, −\cos t⟩\)

    Parameterizations ya urefu wa Arc

    27) Pata kazi ya urefu wa arc\(\vecs s(t)\) kwa sehemu ya mstari iliyotolewa na\(\vecs r(t)=⟨3−3t,\, 4t⟩\). Kisha kuandika parameterization ya urefu wa arc ya\(r\) na\(s\) kama parameter.

    Jibu
    ARC-urefu kazi:\(s(t)=5t\); Arc-urefu parameterization ya\(\vecs r(t)\):\(\vecs r(s)=\left(3−\dfrac{3s}{5}\right)\,\hat{\mathbf{i}}+\dfrac{4s}{5}\,\hat{\mathbf{j}}\)

    28) Parameterize helix\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+ \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) kwa kutumia parameter ya urefu wa arc\(s\), kutoka\(t=0\).

    29) Parameterize curve kwa kutumia parameter ya urefu wa arc\(s\), wakati ambapo\(t=0\)\(\vecs r(t)=e^t \sin t \,\hat{\mathbf{i}} + e^t \cos t \,\hat{\mathbf{j}}\)

    Jibu
    \(\vecs r(s)=\left(1+\dfrac{s}{\sqrt{2}}\right) \sin \left( \ln \left(1+ \dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{i}} +\left(1+ \dfrac{s}{\sqrt{2}}\right) \cos \left( \ln \left(1+\dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{j}}\)

    Curvature na Mzunguko wa Osculating

    30) Kupata curvature ya Curve\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) katika\(t=π/3\). (Kumbuka: Grafu ni duaradufu.)

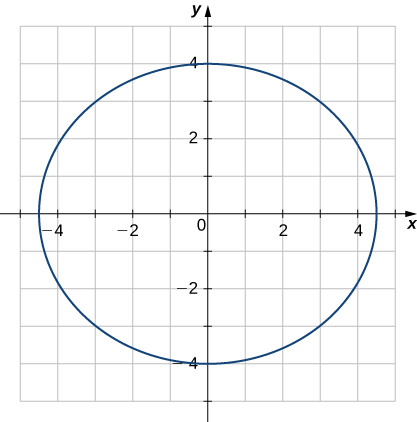
    31) Pata\(x\) -kuratibu ambayo curvature ya curve\(y=1/x\) ni thamani ya juu.

    Jibu
    Thamani ya juu ya curvature hutokea\(x=1\).

    32) Pata curvature ya curve\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+5 \sin t \,\hat{\mathbf{j}}\). Je, curvature inategemea parameter\(t\)?

    33) Kupata curvature\(κ\) kwa Curve\(y=x−\frac{1}{4}x^2\) katika hatua\(x=2\).

    Jibu
    \(\frac{1}{2}\)

    34) Pata curvature\(κ\) kwa curve\(y=\frac{1}{3}x^3\) katika hatua\(x=1\).

    35) Pata curvature\(κ\) ya curve\(\vecs r(t)=t \,\hat{\mathbf{i}}+6t^2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}\). Grafu inavyoonyeshwa hapa:

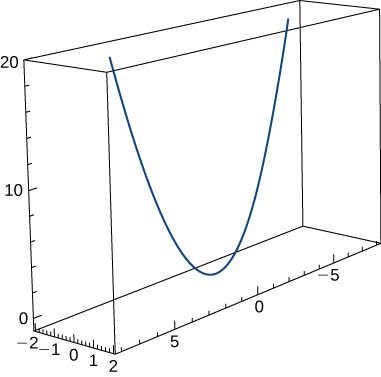
    Jibu
    \(κ≈\dfrac{49.477}{(17+144t^2)^{3/2}}\)

    36) Kupata curvature ya\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩\).

    37) Kupata curvature ya\(\vecs r(t)=\sqrt{2}t \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+e^{−t} \,\hat{\mathbf{k}}\) katika hatua\(P(0,1,1)\).

    Jibu
    \(\frac{1}{2\sqrt{2}}\)

    38) Je! Curve\(y=e^x\) ina kiwango gani cha juu cha curvature?

    39) Ni nini kinachotokea kwa curvature kama\(x→∞\) kwa curve\(y=e^x\)?

    Jibu
    Curvature inakaribia sifuri.

    40) Kupata uhakika wa curvature upeo juu ya Curve\(y=\ln x\).

    41) Kupata equations ya ndege ya kawaida na ndege osculating ya Curve\(\vecs r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩\) katika hatua\((0,π,−2)\).

    Jibu
    \(y=6x+π\)na\(x+6y=6π\)

    42) Pata usawa wa miduara ya osculating ya ellipse\(4y^2+9x^2=36\) kwenye pointi\((2,0)\) na\((0,3)\).

    43) Kupata equation kwa ndege osculating katika hatua\(t=π/4\) juu ya Curve\(\vecs r(t)=\cos (2t) \,\hat{\mathbf{i}}+ \sin (2t) \,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\).

    Jibu
    \(x+2z=\frac{π}{2}\)

    44) Pata radius ya curvature ya\(6y=x^3\) wakati\((2,\frac{4}{3}).\)

    45) Pata curvature kila hatua\((x,y)\) kwenye hyperbola\(\vecs r(t)=⟨a \cosh( t),b \sinh (t)⟩\).

    Jibu
    \(\dfrac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}\)

    46) Tumia hesabu ya helix ya mviringo\(\vecs r(t)=r \sin (t) \,\hat{\mathbf{i}}+r \cos (t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\).

    47) Pata radius ya curvature ya\(y= \ln (x+1)\) saa\((2,\ln 3)\).

    Jibu
    \(\frac{10\sqrt{10}}{3}\)

    48) Pata radius ya curvature ya hyperbola\(xy=1\) kwa uhakika\((1,1)\).

    chembe hatua pamoja Curve ndege\(C\) ilivyoelezwa na\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}\). Tumia parameterization hii kujibu maswali 49 - 51.

    49) Pata urefu wa curve juu ya muda\([0,2]\).

    Jibu
    \(\frac{1}{4}\big[ 4\sqrt{17} + \ln\left(4+\sqrt{17}\right)\big]\text{ units }\approx 4.64678 \text{ units}\)

    50) Kupata curvature ya Curve ndege katika\(t=0,1,2\).

    51) Eleza curvature kama t inavyoongezeka kutoka\(t=0\) juu\(t=2\).

    Jibu
    Curvature inapungua kwa kipindi hiki.

    Upeo wa kikombe kikubwa hutengenezwa kwa kuzunguka grafu ya kazi\(y=0.25x^{1.6}\) kutoka\(x=0\) kwa\(x=5\) karibu\(y\) -axis (kipimo kwa sentimita).

    52) [T] Tumia teknolojia ya kuchora uso.

    53) Kupata curvature\(κ\) ya Curve kuzalisha kama kazi ya\(x\).

    Jibu
    \(κ=\dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\)

    Kumbuka kwamba awali jibu lako linaweza kuwa:
    \(\dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}}\)

    Tunaweza kurahisisha kama ifuatavyo:
    \ (\ kuanza {align*}\ dfrac {6} {25x^ {2/5}\ kushoto (1+\ Frac {4} {25} x^ {6/5}\ haki) ^ {3/2}} &=\ dfrac {6} {25x^ {2/ 5}\ kubwa [\ frac {1} {25}\ kushoto (25+4x^ {6/5}\ haki)\ kubwa] ^ {3/2}}\ [4pt]
    &=\ dfrac {6} {25x^ {2/5}\ kushoto (\ frac {1} {25}\ haki) ^ {3/2}\ kubwa [25+4x^ {6/5}\ kubwa] ^ {3/2}}\\ [4pt]
    &=\ dfrac {6} {\ Frac {25} {125} x^ {2/5}\ kubwa [25+4x^ {6/5}\ kubwa] ^ {3/2}}\ [4pt]
    &=\ dfrac {30} {x^ {2/ 5}\ kushoto (25+4x^ {6/5}\ kulia) ^ {3/2}}\ mwisho {align*}\)

    54) [T] Tumia teknolojia ya kuchora kazi ya curvature.

    Wachangiaji: