13.3: Urefu wa Arc na Curvature

Last updated
Save as PDF

Page ID: 178277

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua urefu wa njia ya chembe katika nafasi kwa kutumia kazi ya urefu wa arc.
Eleza maana ya curvature ya curve katika nafasi na hali formula yake.
Eleza maana ya vectors ya kawaida na ya kawaida ya pembe katika nafasi.

Katika sehemu hii, sisi kujifunza formula kuhusiana na curves katika vipimo mbili na tatu, na kuona jinsi wao ni kuhusiana na mali mbalimbali ya Curve sawa. Kwa mfano, tuseme kazi yenye thamani ya vector inaelezea mwendo wa chembe katika nafasi. Tungependa kuamua jinsi mbali chembe imesafiri juu ya muda uliopewa, ambayo inaweza kuelezewa na urefu wa arc wa njia ifuatayo. Au, tuseme kwamba kazi yenye thamani ya vector inaelezea barabara tunayojenga na tunataka kuamua jinsi kasi ya barabara inavyopatikana. Hii inaelezwa na ukingo wa kazi wakati huo. Sisi kuchunguza kila moja ya dhana hizi katika sehemu hii.

Urefu wa Arc kwa Kazi za Vector

Tumeona jinsi kazi yenye thamani ya vector inaelezea Curve katika vipimo viwili au vitatu. Kumbuka kwamba formula ya urefu wa arc ya curve iliyofafanuliwa na kazi za parametric$x=x(t),y=y(t),t_1≤t≤t_2$ inatolewa na

\[s=\int^{t_2}_{t_1} \sqrt{(x′(t))^2+(y′(t))^2}dt. \nonumber \]

Kwa mtindo sawa, ikiwa tunafafanua curve laini kwa kutumia kazi yenye thamani ya vector$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}$, ambapo$a≤t≤b$, urefu wa arc hutolewa na formula

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2}dt. \nonumber \]

Katika vipimo vitatu, ikiwa kazi ya thamani ya vector inaelezwa na$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$ zaidi ya muda huo huo$a≤t≤b$, urefu wa arc hutolewa na

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2+(h′(t))^2}dt. \nonumber \]

Theorem: Arc-Length Formula kwa ndege na nafasi curves

Ndege Curve: Kutokana Curve laini$C$ inavyoelezwa na kazi$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \, \hat{\mathbf{j}}$, ambapo$t$ uongo ndani ya muda$[a,b]$, safu urefu wa$C$ zaidi ya muda ni

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc2D}\end{align} \]

Nafasi Curve: Kutokana Curve laini$C$ inavyoelezwa na kazi$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$, ambapo$t$ uongo ndani ya muda$[a,b]$, urefu safu ya$C$ zaidi ya muda ni

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align} \]

Njia mbili ni sawa sana; zinatofautiana tu kwa ukweli kwamba pembe ya nafasi ina kazi tatu za sehemu badala ya mbili. Kumbuka kwamba formula hufafanuliwa kwa curves laini: curves ambapo kazi yenye thamani ya vector$\vecs r(t)$ inatofautiana na derivative isiyo ya sifuri. Hali ya urembo inathibitisha kwamba Curve haina cusps (au pembe) ambayo inaweza kufanya formula tatizo.

Mfano$\PageIndex{1}$: Finding the Arc Length

Tumia urefu wa arc kwa kila kazi zifuatazo za thamani ya vector:

$\vecs r(t)=(3t−2) \,\hat{\mathbf{i}}+(4t+5) \,\hat{\mathbf{j}},\quad 1≤t≤5$
$\vecs r(t)=⟨t\cos t,t\sin t,2t⟩,0≤t≤2 \pi $

Suluhisho

Kutumia Equation\ ref {Arc2D}$\vecs r′(t)=3 \,\hat{\mathbf{i}}+4 \,\hat{\mathbf{j}}$, hivyo
\[\begin{align*} s &=\int^{b}_{a} \|\vecs r′(t)\|dt \\[4pt] &=\int^{5}_{1} \sqrt{3^2 + 4^2} dt \\[4pt] &=\int^{5}_{1} 5 dt = 5t\big|^{5}_{1} = 20. \end{align*}\]
Kutumia Equation\ ref {Arc3D}$\vecs r′(t)=⟨ \cos t−t \sin t, \sin t+t \cos t,2⟩ $, hivyo
\[\begin{align*} s &=\int^{b}_{a} ∥\vecs r′(t)∥dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{(\cos t−t \sin t)^2+( \sin t+t \cos t)^2+2^2} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{( \cos ^2 t−2t \sin t \cos t+t^2 \sin ^2 t)+( \sin^2 t+2t \sin t \cos t+t^2 \cos ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{\cos ^2 t+ \sin^2 t+t^2( \cos ^2 t+ \sin ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{t^2+5} dt\end{align*}\]

Hapa tunaweza kutumia formula ya ushirikiano wa meza

\[\int \sqrt{u^2+a^2}du = \dfrac{u}{2}\sqrt{u^2+a^2} + \dfrac{a^2}{2} \ln \,\left|\, u + \sqrt{u^2+a^2} \,\right| + C, \nonumber \]

hivyo tunapata

\[\begin{align*} \int^{2 \pi}_{0} \sqrt{t^2+5} dt \; &= \frac{1}{2} \bigg( t \sqrt{t^2+5}+5 \ln \,\left|t+\sqrt{t^2+5}\right| \bigg) _0^{2π} \\[4pt] &= \frac{1}{2} \bigg( 2π \sqrt{4π^2+5}+5 \ln \bigg( 2π+ \sqrt{4π^2+5} \bigg) \bigg)−\frac{5}{2} \ln \sqrt{5} \\[4pt] &≈25.343 \,\text{units}. \end{align*}\]

Zoezi$\PageIndex{1}$

Tumia urefu wa arc wa safu ya parameterized

\[\vecs r(t)=⟨2t^2+1,2t^2−1,t^3⟩,\quad 0≤t≤3. \nonumber \]

Kidokezo: Tumia Equation\ ref {Arc3D}.
Jibu: $\vecs r′(t)=⟨4t,4t,3t^2⟩,$hivyo$s= \frac{1}{27}(113^{3/2}−32^{3/2})≈37.785$ vitengo

Sasa tunarudi kwenye helix iliyoletwa mapema katika sura hii. Kazi yenye thamani ya vector inayoelezea helix inaweza kuandikwa kwa fomu

\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}} +R \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t≤h, \nonumber \]

ambapo$R$ inawakilisha radius ya helix,$h$ inawakilisha urefu (umbali kati ya zamu mbili mfululizo), na helix inakamilisha$N$ zamu. Hebu hupata formula kwa urefu wa safu ya helix hii kwa kutumia Equation\ ref {Arc3D}. Awali ya yote,

\[\vecs r′(t)=−\dfrac{2πNR}{h} \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}}+ \dfrac{2πNR}{h} \cos \left(\dfrac{2πNt}{h} \right) \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}. \nonumber \]

Kwa hiyo,

\[\begin{align*} s & =\int_a^b ‖\vecs r′(t)‖dt \\[4pt] &=\int_0^h\sqrt{ \bigg(−\dfrac{2πNR}{h} \sin \bigg(\dfrac{2πNt}{h} \bigg) \bigg)^2+ \bigg( \dfrac{2πNR}{h} \cos \bigg( \dfrac{2πNt}{h} \bigg) \bigg)^2+1^2}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} \bigg( \sin ^2 \bigg(\dfrac{2πNt}{h} \bigg) + \cos ^2 \bigg( \dfrac{2πNt}{h} \bigg) \bigg)+1}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}dt \\[4pt] &=\bigg[ t\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}\bigg]^h_0 \\[4pt] &=h \sqrt{ \dfrac{4π^2N^2R^2 + h^2}{h^2}} \\[4pt] &=\sqrt{ 4π^2N^2R^2 + h^2}.\end{align*}\]

Hii inatoa formula kwa urefu wa waya inahitajika kuunda helix na$N$ zamu ambayo ina radius$R$ na urefu$h$.

Parameterization ya Arc-Length

Sasa tuna formula kwa urefu wa arc ya Curve inavyoelezwa na kazi yenye thamani ya vector. Hebu tuchukue hatua hii moja zaidi na tuchunguze ni kazi gani ya urefu wa arc.

Ikiwa kazi yenye thamani ya vector inawakilisha nafasi ya chembe katika nafasi kama kazi ya muda, basi kazi ya urefu wa arc inapima umbali gani chembe hiyo inasafiri kama kazi ya wakati. Fomu ya kazi ya urefu wa arc ifuatavyo moja kwa moja kutoka kwa formula ya urefu wa arc:

\[s=\int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du. \label{arclength2} \]

Ikiwa curve iko katika vipimo viwili, basi maneno mawili tu yanaonekana chini ya mizizi ya mraba ndani ya muhimu. Sababu ya kutumia variable huru u ni kutofautisha kati ya muda na variable ya ushirikiano. Tangu$s(t)$ hatua umbali alisafiri kama kazi ya muda,$s′(t)$ hatua kasi ya chembe wakati wowote. Kwa kuwa tuna formula$s(t)$ kwa equation\ ref {arclength2}, tunaweza kutofautisha pande zote mbili za equation:

\[ \begin{align*} s′(t) &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du \bigg] \\[4pt] &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.\end{align*}\]

Ikiwa tunadhani kwamba$\vecs r(t)$ inafafanua safu ya laini, basi urefu wa arc unaongezeka daima, hivyo$s′(t)>0$$t>a$. Mwisho, ikiwa$\vecs r(t)$ ni Curve ambayo$\|\vecs r′(t)\|=1 $ kwa wote$t$, basi

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du=\int^{t}_{a} 1\,du=t−a, \nonumber \]

ambayo ina maana kwamba$t$ inawakilisha urefu safu kwa muda mrefu kama$a=0$.

Theorem: Kazi ya Urefu wa Arc

Hebu$\vecs r(t)$ kuelezea Curve laini kwa$t≥a$. Kisha kazi ya urefu wa arc hutolewa na

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du \nonumber \]

Zaidi ya hayo,

\[\dfrac{ds}{dt}=‖\vecs r′(t)‖>0. \nonumber \]

Ikiwa$‖\vecs r′(t)‖=1$ kwa wote$t≥a$, basi parameter$t$ inawakilisha urefu wa arc kutoka mwanzo$t=a$.

Matumizi muhimu ya theorem hii ni kupata parameterization mbadala ya curve iliyotolewa, inayoitwa parameterization ya urefu wa arc. Kumbuka kwamba kazi yoyote ya thamani ya vector inaweza reparameterized kupitia mabadiliko ya vigezo. Kwa mfano, ikiwa tuna kazi$\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π$ ambayo inaweka mduara wa radius 3, tunaweza kubadilisha parameter kutoka$t$ kwa$4t$, kupata parameterization mpya$\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩$. Parameterization mpya bado inafafanua mduara wa radius 3, lakini sasa tunahitaji tu kutumia maadili ya$0≤t≤π/2$ kupitisha mduara mara moja.

Tuseme kwamba sisi kupata kazi Arc-urefu$s(t)$ na ni uwezo wa kutatua kazi hii kwa ajili ya$t$ kama kazi ya$s$. Tunaweza kisha reparameterize kazi ya awali$\vecs r(t)$ na badala ya kujieleza kwa$t$ nyuma katika$\vecs r(t)$. Kazi ya thamani ya vector sasa imeandikwa kwa suala la parameter$s$. Kwa kuwa kutofautiana$s$ inawakilisha urefu wa arc, tunaita hii parameterization ya urefu wa arc ya kazi ya awali$\vecs r(t)$. Faida moja ya kutafuta parameterization ya urefu wa arc ni kwamba umbali uliosafiri kando ya pembe kuanzia sasa$s=0$ ni sawa na parameter$s$. Parameterization ya urefu wa arc pia inaonekana katika mazingira ya curvature (ambayo sisi kuchunguza baadaye katika sehemu hii) na mstari integrals.

Mfano$\PageIndex{2}$: Finding an Arc-Length Parameterization

Pata parameterization ya urefu wa arc kwa kila moja ya curves zifuatazo:

$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0$
$\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3$

Suluhisho

Kwanza tunapata kazi ya urefu wa arc kwa kutumia Equation\ ref {arclength2}:
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u,4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*}\]
ambayo inatoa uhusiano kati ya urefu wa arc$s$ na parameter$t$ kama$s=4t;$ hivyo,$t=s/4$. Kisha sisi kuchukua nafasi ya kutofautiana$t$ katika kazi ya awali$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}$ na$s/4$ kujieleza kupata
\[\vecs r(s)=4 \cos \left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin \left( \frac{s}{4}\right) \,\hat{\mathbf{j}}. \nonumber \]
Hii ni parameterization ya urefu wa arc ya$\vecs r(t)$. Tangu kizuizi awali juu ya$t$ ilitolewa na$t≥0$, kizuizi juu ya s inakuwa$s/4≥0$, au$s≥0$.
Kazi ya urefu wa arc inatolewa na Equation\ ref {arclength2}:
\[\begin{align*} s(t) & = \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_3^t ‖⟨1,2,2⟩‖ \,du \\[4pt] &= \int_3^t \sqrt{1^2+2^2+2^2} \,du \\[4pt] &= \int_3^t 3 \,du \\[4pt] &= 3t - 9. \end{align*}\]
Kwa hiyo, uhusiano kati ya urefu wa arc$s$ na parameter$t$ ni$s=3t−9$, hivyo$t= \frac{s}{3}+3$. Kubadilisha hii katika$\vecs r(t)=⟨t+3,2t−4,2t⟩ $ mazao ya awali ya kazi
\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)−4,\,2\left(\frac{s}{3}+3\right)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s}{3}+6⟩.\nonumber \]
Hii ni parameterization ya urefu wa arc ya$\vecs r(t)$. Kizuizi cha awali kwenye parameter$t$ kilikuwa$t≥3$, hivyo kizuizi$s$ ni$(s/3)+3≥3$, au$s≥0$.

Zoezi$\PageIndex{2}$

Pata kazi ya urefu wa arc kwa helix

\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad t≥0. \nonumber \]

Kisha, tumia uhusiano kati ya urefu wa arc na parameter$t$ ili kupata parameterization ya urefu wa arc ya$\vecs r(t)$.

Kidokezo

Anza kwa kutafuta kazi ya urefu wa arc.

Jibu

$s=5t$, au$t=s/5$. Kubadilisha hii katika$\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩$ anatoa

\[\vecs r(s)=⟨3 \cos \left(\frac{s}{5}\right),3 \sin \left(\frac{s}{5}\right),\frac{4s}{5}⟩,\quad s≥0 \nonumber \]

Uvunjaji

Mada muhimu kuhusiana na urefu wa arc ni curvature. Dhana ya curvature hutoa njia ya kupima jinsi kasi ya laini inavyogeuka. Mduara una curvature ya mara kwa mara. Kidogo cha radius ya mduara, zaidi ya curvature.

Fikiria kuendesha gari barabarani. Tuseme barabara iko kwenye arc ya mduara mkubwa. Katika kesi hiyo ungependa kugeuka gurudumu ili uendelee barabara. Sasa tuseme radius ni ndogo. Katika kesi hii unahitaji kurejea kwa kasi zaidi ili uendelee barabara. Katika kesi ya Curve zaidi ya mduara, mara nyingi ni muhimu kwanza kuandika mduara kwa Curve katika hatua fulani ili ni tangent kwa Curve katika hatua hiyo na “hukumbatia” Curve kwa karibu iwezekanavyo katika kitongoji cha uhakika (Kielelezo$\PageIndex{1}$). Upepo wa grafu katika hatua hiyo hufafanuliwa kuwa sawa na ukingo wa mduara ulioandikwa.

Takwimu hii ni grafu ya pembe. Curve inaongezeka na huanguka katika quadrant ya kwanza. Pamoja na curve, ambapo Curve inabadilika kutoka kupungua hadi kuongezeka kuna mduara. Chini ya mviringo hupiga sawa na grafu ya curve. Pia kuna mduara wa pili mdogo ambapo Curve huenda kutoka kuongezeka hadi kupungua. Sehemu ya mduara huanguka kwenye pembe. Wote duru na r Radius kuwakilishwa. — Kielelezo$\PageIndex{1}$: Grafu inawakilisha curvature$y=f(x).$ ya kazi Kali ya kugeuka kwenye grafu, zaidi ya curvature, na ndogo radius ya mduara ulioandikwa.

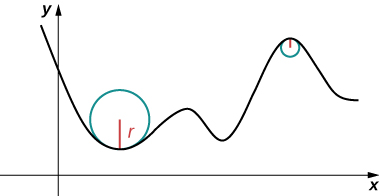
Ufafanuzi: curvature

Hebu$C$ kuwa curve laini katika ndege au katika nafasi iliyotolewa na$\vecs r(s)$, wapi$s$ parameter arc-urefu. Curvature$κ$ katika$s$ ni

\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T′(s)‖. \nonumber \]

Tembelea video hii kwa maelezo zaidi kuhusu ukingo wa pembe ya nafasi.

Fomu katika ufafanuzi wa curvature sio muhimu sana kwa suala la hesabu. Hasa, kukumbuka kwamba$\vecs T(t)$ inawakilisha kitengo tangent vector kwa kupewa kazi vector-thamani$\vecs r(t)$, na formula kwa$\vecs T(t)$ ni

\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}. \nonumber \]

Ili kutumia formula ya curvature, ni muhimu kwanza kuelezea$\vecs r(t)$ kwa mujibu wa parameter ya urefu wa arc$s$, kisha kupata kitengo cha tangent vector$\vecs T(s)$ kwa kazi$\vecs r(s)$, kisha kuchukua derivative ya kwa heshima$\vecs T(s)$ na$s$. Huu ni mchakato wa kuchochea. Kwa bahati nzuri, kuna kanuni sawa za curvature.

Theorem: Njia Mbadala za Curvature

Ikiwa$C$ ni curve laini iliyotolewa na$\vecs r(t)$, basi curvature$κ$ ya$C$ at$t$ inapewa na

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}. \label{EqK2} \]

Ikiwa$C$ ni curve tatu-dimensional, basi curvature inaweza kutolewa kwa formula

\[κ =\dfrac{‖\vecs r′(t)×\vecs r′′(t)‖}{‖\vecs r′(t)‖^3}.\label{EqK3} \]

Ikiwa$C$ ni grafu ya kazi$y=f(x)$ na zote mbili$y′$ na$y''$ zipo, basi curvature$κ$ katika hatua$(x,y)$ hutolewa na

\[κ =\dfrac{|y''|}{[1+(y′)^2]^{3/2}}.\label{EqK4} \]

Ushahidi

Fomu ya kwanza ifuatavyo moja kwa moja kutoka kwa utawala wa mnyororo:

\[\dfrac{d\vecs{T}}{dt} = \dfrac{d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber \]

$s$wapi urefu wa arc kando ya pembe$C$. Kugawanya pande zote mbili kwa$ds/dt$, na kuchukua ukubwa wa pande zote mbili inatoa

\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T′(t)}{\dfrac{ds}{dt}}\right\rVert.\nonumber \]

Kwa kuwa$ds/dt=‖\vecs r′(t)‖$, hii inatoa formula kwa curvature$κ$ ya curve$C$ kwa suala la parameterization yoyote ya$C$:

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}.\nonumber \]

Katika kesi ya curve tatu-dimensional, tunaanza na formula$\vecs T(t)=(\vecs r′(t))/‖\vecs r′(t)‖$ na$ds/dt=‖\vecs r′(t)‖$. Kwa hiyo,$\vecs r′(t)=(ds/dt)\vecs T(t)$. Tunaweza kuchukua derivative ya kazi hii kwa kutumia formula ya bidhaa ya scalar:

\[\vecs r″(t)=\dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t).\nonumber \]

Kutumia equations hizi mbili za mwisho tunapata

\[\begin{align*} \vecs r′(t)×\vecs r″(t) &=\dfrac{ds}{dt}\vecs T(t)× \bigg( \dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t) \bigg) \\[4pt] &=\dfrac{ds}{dt} \dfrac{d^2s}{dt^2}\vecs T(t)×\vecs T(t)+(\dfrac{ds}{dt})^2\vecs T(t)×\vecs T′(t). \end{align*}\]

Tangu$\vecs T(t)×\vecs T(t)=0$, hii inapunguza

\[\vecs r′(t)×\vecs r′′(t)=\left(\dfrac{ds}{dt}\right)^2\vecs T(t)×\vecs T′(t).\nonumber \]

Kwa kuwa$\vecs T′$ ni sambamba na$\vecs N$, na$\vecs T$ ni orthogonal kwa$\vecs N$, inafuata kwamba$\vecs T$ na$\vecs T′$ ni orthogonal. Hii ina maana kwamba$‖\vecs T×\vecs T′‖=‖\vecs T‖‖\vecs T′‖ \sin (π/2)=‖\vecs T′‖$, hivyo

\[\|\vecs r′(t)×\vecs r″(t)\|=\left(\dfrac{ds}{dt}\right)^2‖\vecs T′(t)‖.\nonumber \]

Sasa sisi kutatua equation hii kwa$‖\vecs T′(t)‖$ na kutumia ukweli kwamba$ds/dt=‖\vecs r′(t)‖$:

\[‖\vecs T′(t)‖=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^2}.\nonumber \]

Kisha, tunagawanya pande zote mbili$‖\vecs r′(t)‖$. Hii inatoa

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}.\nonumber \]

Hii inathibitisha$\ref{EqK3}$. Ili kuthibitisha$\ref{EqK4}$, tunaanza na dhana kwamba Curve$C$ inafafanuliwa na kazi$y=f(x)$. Kisha, tunaweza kufafanua$\vecs r(t)=x \,\hat{\mathbf{i}}+f(x) \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Kutumia formula ya awali ya curvature:

\[\begin{align*} \vecs r′(t) &=\,\hat{\mathbf{i}}+f′(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r″(t) &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f′(x) & 0 \\ 0 & f″(x) & 0 \end{vmatrix} =f″(x)\,\hat{\mathbf{k}}. \end{align*}\]

Kwa hiyo,

\[κ= \dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}=\dfrac{|f″(x)|}{(1+[f′(x)]^2)^{3/2}} \nonumber \]

Mfano$\PageIndex{3}$: Finding Curvature

Kupata curvature kwa kila moja ya curves zifuatazo katika hatua fulani:

$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}+4 \sin t\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}},\quad t=\dfrac{4π}{3}$
$\mathrm{f(x)= \sqrt{4x−x^2},x=2}$

Suluhisho

Kazi hii inaelezea helix.

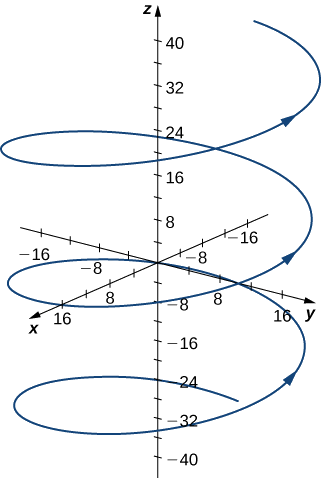
$Takwimu hii ni grafu ya pembe katika vipimo 3. Curve ni helix inayozunguka mhimili wa z. Inaanza chini ya ndege ya xy na inazunguka na mwelekeo.$

Curvature ya helix katika$t=(4π)/3$ inaweza kupatikana kwa kutumia$\ref{EqK2}$. Kwanza, hesabu$\vecs T(t)$:

\[\begin{align*} \vecs T(t) &=\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖} \\[4pt] &=\dfrac{⟨−4 \sin t,4 \cos t,3⟩}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+3^2}}\\[4pt] &=⟨−\dfrac{4}{5} \sin t,\dfrac{4}{5} \cos t, \dfrac{3}{5}⟩. \end{align*}\]

Ifuatayo, hesabu$\vecs T′(t):$

\[\vecs T′(t)=⟨−\dfrac{4}{5} \cos t,− \dfrac{4}{5} \sin t,0⟩. \nonumber \]

Mwisho, tumia$\ref{EqK2}$:

\[ \begin{align*} κ &=\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} = \dfrac{‖⟨−\dfrac{4}{5} \cos t,−\dfrac{4}{5} \sin t,0⟩‖}{‖⟨−4 \sin t,4 \cos t,3⟩‖} \\[4pt] &=\dfrac{\sqrt{(−\dfrac{4}{5} \cos t)^2+(−\dfrac{4}{5} \sin t)^2+0^2}}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+ 3^2}} \\[4pt] &=\dfrac{4/5}{5}=\dfrac{4}{25}. \end{align*}\]

Curvature ya helix hii ni mara kwa mara katika pointi zote juu ya helix.

Kazi hii inaelezea semicircle.

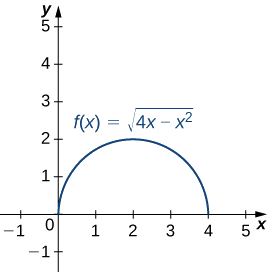
$Takwimu hii ni grafu ya semicircle. Ni katika quadrant ya kwanza. Semicircle huanza katika asili na inacha saa 4 kwenye x-axis. Semicircle inawakilisha kazi f (x) = mizizi ya mraba ya (4x-x ^ 2).$

Ili kupata curvature ya grafu hii, tunapaswa kutumia$\ref{EqK4}$. Kwanza, tunahesabu$y′$ na$y″:$

\[\begin{align*}y &=\sqrt{4x−x^2}=(4x−x^2)^{1/2} \\[4pt] y′ &=\dfrac{1}{2}(4x−x^2)^{−1/2}(4−2x)=(2−x)(4x−x^2)^{−1/2} \\[4pt] y″ &=−(4x−x^2)^{−1/2}+(2−x)(−\dfrac{1}{2})(4x−x^2)^{−3/2}(4−2x) \\[4pt] & =−\dfrac{4x−x^2}{(4x−x^2)^{3/2}}− \dfrac{(2−x)^2}{(4x−x^2)^{3/2}} \\[4pt] &=\dfrac{x^2−4x−(4−4x+x^2)}{(4x−x^2)^{3/2}} \\[4pt] &=−\dfrac{4}{(4x−x^2)^{3/2}}. \end{align*} \nonumber \]

Kisha, tunatumia$\ref{EqK4}$:

\[ \begin{align*} κ &=\dfrac{|y''|}{[1+(y′)^2]^{3/2}} \\[4pt] &= \dfrac{\bigg| −\dfrac{4}{(4x−x^2)^{3/2}}\bigg|}{\bigg[1+((2−x)(4x−x^2)^{−1/2})^2 \bigg]^{3/2}} = \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{\bigg[ 1+\dfrac{(2−x)^2}{4x−x^2} \bigg]^ {3/2}} \\[4pt] &= \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{ \bigg[ \dfrac{4x−x^2+x^2−4x+4}{4x−x^2} \bigg]^{3/2}}=\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg| ⋅\dfrac{(4x−x^2)^{3/2}}{8} \\[4pt] &=\dfrac{1}{2}. \end{align*}\]

Upepo wa mduara huu ni sawa na usawa wa radius yake. Kuna suala madogo na thamani kamili katika$\ref{EqK4}$; hata hivyo, kuangalia kwa karibu hesabu inaonyesha kwamba denominator ni chanya kwa thamani yoyote ya$x$.

Zoezi$\PageIndex{3}$

Kupata curvature ya Curve defined na kazi

\[y=3x^2−2x+4 \nonumber \]

katika hatua$x=2$.

Kidokezo: Tumia$\ref{EqK4}$.
Jibu: $κ \; =\frac{6}{101^{3/2}}≈0.0059$

Vectors Kawaida na Binormal

Tumeona kwamba derivative$\vecs r′(t)$ ya kazi ya thamani ya vector ni vector tangent kwa Curve inavyoelezwa na$\vecs r(t)$, na kitengo tangent vector$\vecs T(t)$ inaweza kuhesabiwa kwa kugawa$\vecs r′(t)$ kwa ukubwa wake. Wakati wa kusoma mwendo katika vipimo vitatu, wadudu wengine wawili ni muhimu katika kuelezea mwendo wa chembe kando ya njia katika nafasi: kitengo kuu vector kawaida na vector binormal.

Ufafanuzi: Vectors Binormal

Hebu$C$ kuwa curve tatu-dimensional laini kuwakilishwa na$\vecs r$ zaidi ya muda wazi$I$. Kama$\vecs T′(t)≠\vecs 0$, basi kitengo kuu vector kawaida katika$t$ ni defined kuwa

\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \label{EqNormal} \]

Vector binormal katika$t$ inaelezwa kama

\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal} \]

$\vecs T(t)$wapi kitengo cha tangent vector.

Kumbuka kwamba, kwa ufafanuzi, vector binormal ni orthogonal kwa vector kitengo tangent na vector kawaida. Zaidi ya hayo,$\vecs B(t)$ daima kitengo vector. Hii inaweza kuonyeshwa kwa kutumia formula kwa ukubwa wa bidhaa ya msalaba.

\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta, \nonumber \]

$\theta$wapi pembe kati$\vecs T(t)$ na$\vecs N(t)$. Kwa kuwa$\vecs N(t)$ ni derivative ya vector kitengo, mali (vii) ya derivative ya kazi yenye thamani ya vector inatuambia kwamba$\vecs T(t)$ na$\vecs N(t)$ ni orthogonal kwa kila mmoja, hivyo$\theta=π/2$. Zaidi ya hayo, wote ni wadudu kitengo, hivyo ukubwa wao ni 1. Kwa hiyo,$‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/2)=1$ na$\vecs B(t)$ ni kitengo vector.

Kitengo kuu vector kawaida inaweza kuwa changamoto kwa mahesabu kwa sababu kitengo tangent vector inahusisha quotient, na quotient hii mara nyingi ina mizizi mraba katika denominator. Katika kesi tatu-dimensional, kutafuta bidhaa msalaba wa kitengo tangent vector na kitengo kawaida vector inaweza kuwa mbaya zaidi. Kwa bahati nzuri, tuna formula mbadala kwa ajili ya kutafuta wadudu hawa wawili, na wao ni iliyotolewa katika Motion in Space.

Mfano$\PageIndex{4}$: Finding the Principal Unit Normal Vector and Binormal Vector

Kwa kila moja ya kazi zifuatazo za thamani ya vector, pata kitengo kuu cha vector ya kawaida. Kisha, ikiwa inawezekana, pata vector ya binormal.

$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}− 4 \sin t\,\hat{\mathbf{j}}$
$\vecs r(t)=(6t+2)\,\hat{\mathbf{i}}+5t^2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf{k}}$

Suluhisho

Kazi hii inaelezea mduara.

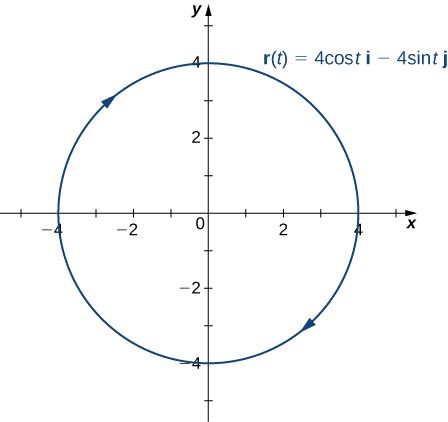
$Takwimu hii ni grafu ya mduara unaozingatia asili na radius ya 2. Mwelekeo wa mduara ni saa ya saa. Inawakilisha vector-thamani kazi r (t) = 4costi - 4 sintj.$

Ili kupata kitengo kuu vector kawaida, sisi kwanza lazima kupata kitengo tangent vector$\vecs T(t):$

\ [kuanza {align*}\ vecs T (t) &=\ dfrac {\ vecs r′ (t)} {合\\ vecs r′ (t)}\\ [4pt]
&=\ dfrac {-4\ sin t\,\ kofia {\ mathbf {i}}} {\ sqrt {(-4\ sin t) ^2+ (-4\ cos t) ^2}}\\ [4pt]
&=\ dfrac {-4\ sin t\,\ kofia {\ mathbf {i}}} -4\ cos t\,\ kofia {\ hesabu {j}} {\ sqrt {16\ dhambi ^2 t+16\ cos ^2 t}}\\ [4pt]
&=\ dfrac {-4\ sin t\,\ kofia {\ mathbf {i}} -4\ cos t\,\ kofia {\ mathbf {j}}} {\ sqrt {16 (\ dhambi ^2 t+\ cos ^2 t)}}\\ [4pt]
&=\ dfrac {16-4\ sin t\,\ kofia {\ mathbf {i}} -4\ cos t\,\ kofia {\ mathbf {j}}} {4}\\[4pt] &=− \sin t\,\hat{\mathbf{i}}− \cos t\,\hat{\mathbf{j}}.\end{align*}\]

Kisha, tunatumia$\ref{EqNormal}$:

\ [kuanza {align*}\ vecs N (t) &=\ dfrac {\ vecs T( t)} {合\ vecs T( t)}\\ [4pt] &=\ dfrac {}\ cos t\,\ kofia {\ mathbf {i}}}\ sqrt {-\ cos t) ^2+ (\ sin t) ^2}}\\ [4pt]
&=\ dfrac {合\ cos t\,\ kofia {\ hisabati {i}} +\ dhambi t\,\ kofia {\ hesabu {j}} {\ sqrt {\ sqrt {\ cos ^2 t+\ dhambi ^2 t}}\\ [4pt]
&=\\ cos t\,\ kofia {\ mathbf {i}} +\ sin t\,\ kofia {\ mathbf {j}}. \ mwisho {align*}\]

Kumbuka kwamba kitengo tangent vector na kuu kitengo kawaida vector ni orthogonal kwa kila mmoja kwa maadili yote ya$t$:

\[\begin{align*} \vecs T(t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt] &= \sin t \cos t−\cos t \sin t \\[4pt] &=0. \end{align*}\]

Zaidi ya hayo, kuu kitengo kawaida vector pointi kuelekea katikati ya mduara kutoka kila hatua kwenye mduara. Tangu$\vecs r(t)$ inafafanua Curve katika vipimo viwili, hatuwezi kuhesabu vector binormal.

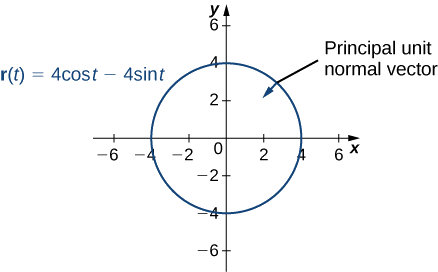
$Takwimu hii ni grafu ya mduara unaozingatia asili na radius ya 2. Mwelekeo wa mduara ni saa ya saa. Inawakilisha vector-thamani kazi r (t) = 4costi - 4 sintj. Kwenye mduara katika quadrant ya kwanza ni vector inayoelezea ndani. Ni kinachoitwa “kuu kitengo kawaida vector”.$

Kazi hii inaonekana kama hii:

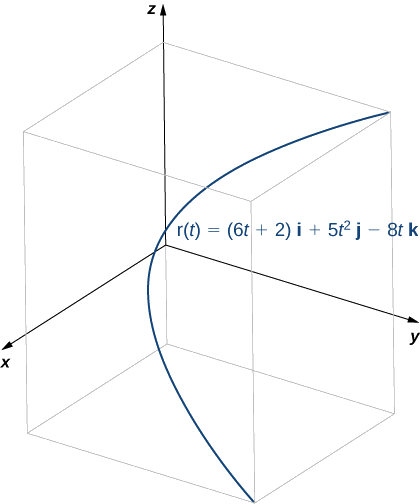
$Takwimu hii ni safu katika vipimo 3. Ni ndani ya sanduku. Sanduku linawakilisha octant ya kwanza. Curve huanza chini ya kulia ya sanduku na curves kupitia sanduku katika Curve parabolic hadi juu.$

Ili kupata kitengo kuu vector kawaida, sisi kwanza kupata kitengo tangent vector$\vecs T(t):$

\ [kuanza {align*}\ vecs T (t) &=\ dfrac {\ vecs r′ (t)} {\ vecs\ vecs r′ (t)}\\ [4pt]
&=\ dfrac {6\,\ kofia {\ mathbf {i}} +10t\,\ kofia {\ mathbf {j}} -8\,\ kofia {\ mathbf {i}\ mathbf {k}}} {\ sqrt {6^2+ (10t) ^2+ (-8) ^2}}\\ [4pt]
&=\ dfrac {6\,\ kofia {\ mathbf {i}} +10t\,\ kofia {\ mathbf {j}} -8\,\ kofia {\ mathbf {k}}} {\ sqrt {36+100t ^ 2+64 }}\\ [4pt]
&=\ dfrac {6\,\ kofia {\ mathbf {i}} +10t\,\ kofia {\ mathbf {j}} -8\,\ kofia {\ mathbf {k}} {\ sqrt {100 (t ^ 2+1)}}\\ [4pt]
&=\ dfrac {3\,\ kofia {\ mathbf {i}} -5t\,\ kofia {\ mathbf {j}} -4\,\ kofia {\ mathbf {k}} {5\ sqrt {t ^ 2+1}}\\ [4pt]
&=\ dfrac {3} {5} (t ^ 2+1) ^ {-1/2}\,\ kofia {\ math {3} {5} (t ^ 2+1) ^ {-1/2}\,\ kofia {\ math {3} {3} {5} (t ^ 2+1)\\ bf {i}} -t (t ^ 2 +1) ^ {-1/2}\,\ kofia {\ mathbf {j}}} -\ dfrac {4} {5} (t ^ 2+1) ^ {-1/2}\,\ kofia {\ mathbf {k}}}. \ mwisho {align*}\]

Kisha, tunahesabu$\vecs T′(t)$ na$‖\vecs T′(t)‖$:

\ [kuanza {align*}\ vecs T( t) &=\ dfrac {3} {5} (合\ dfrac {1} {2}) (t ^ 2+1) ^ {-3/2} (2t)\,\ kofia {\ mathbf {i}} (t ^ 2+1) ^ {-1/2} -t (\ dfrac {1} {2}) (t ^ 2+1) ^ {-3/2} (2t))\,\ kofia {\ mathbf {j}}} -\ dfrac {4} {5} (∙\ dfrac {1} {2}) (t ^ 2+1) ^ {-3/2} (2t)\\ kofia {k} {k}\\ [4pt]
&=\\ dfrac {3t} {5 (t ^ 2+1) ^ {3/2}}\,\ kofia {\ mathbf {i}}}}\ dfrac { 1} {(t ^ 2+1) ^ {3/2}}\,\ kofia {j}} +\ dfrac {4t} {5 (t ^ 2+1) ^ {3/2}}\,\ kofia {\ hisabati {k}}\\ [4pt]}\\ vecs T( t)} &=\ sqrt {\ kubwa (drac {3t} {5 (t ^ 2+1) ^ {3/2}}\ kubwa) ^2+\ kubwa (合\ drac {1} {(t ^ 2+1) ^ {3/2}}\ kubwa) ^2+\ kubwa (\ drac {4t} {5 (t ^ 2+1) ^ {3/2}\ kubwa) ^2}\ [4pt]
&=\ sqrt {\ dfrac {9t ^ 2} {25 (t ^ 2+1) ^3} +\ dfrac {1} {(t ^ 2+1) ^3} +\ dfrac {16t ^ 2} {25 (t ^ 2+1) ^3}}\\ [4pt]
&=\ sqrt {\ dfrac {25t ^ 2+25} {25 (t ^ 2+1) ^3}}\\ [4pt]
&=\ sqrt {1} {(t ^ 2+1) ^2}}\\ [4pt]
&=\ dfrac {1} {t ^ 2+1}. \ mwisho {align*}\]

Kwa hiyo, kulingana na$\ref{EqNormal}$:

\ [kuanza {align*}\ vecs N (t) &=\ dfrac {\ vecs T (t)} {合\ vecs T( t)}\\ [4pt]
&=\ kubwa (-\ drac {3t} {5 (t ^ 2+1) ^ {3/2}}\,\ kofia {\ mathbf {i}} dfrac {1} {(t ^ 2+1) ^ {3/2}}\,\ kofia {\ mathbf {j}} +\ dfrac {4t} {5 (t ^ 2+1) ^ {3/2}}\,\ kofia {\ hisabati {k}}\ kubwa) (t ^ 2+1)\ [4pt]
&=\ dfrac {3t} {5 (t ^ 2+1) ^ {1/2}}\,\ kofia {\ mathbf {i}}} -\ dfrac {5} {5 (t ^ 2+1) ^ {1/2}}\,\ kofia {\ mathbf {j}} +\ dfrac {4t} {5 (t ^ 2+1) ^ {1/2}}\,\ kofia {\ mathbf {k}}\\ [4pt]
&=// c {3t\,\ kofia {\ mathbf {i}} +5\,\ kofia {\ mathbf {j}} -4t\,\ kofia {\ mathbf {k}} {5\ sqrt {t^2+1}}}. \ mwisho {align*}\]

Mara nyingine tena, kitengo tangent vector na kitengo kuu kawaida vector ni orthogonal kwa kila mmoja kwa maadili yote ya$t$:

\ [kuanza {align*}\ vecs T (t) ·\ vecs N (t) &=\ kubwa (\ dfrac {3\,\ kofia {\ mathbf {i}} -5t\,\ kofia {j}} -4\,\ kofia {\ mathbf {k}}} {5\ sqrt {t ^ 2+1}}}\ kubwa) ·\ kubwa (-\ drac {3t\,\ kofia {\ mathbf {i}} +5\,\ kofia {\ mathbf {j}} -4t\,\ kofia {k}} {k}} {5\ sqrt {t ^ 2+1}}\ kubwa)\\ [4pt]
&=\ drac 3 (-3t) -5t (-5) -4 (4t)} {25 (t ^ 2+1)} \\ [4pt]
&=\ dfrac {-9t+25t-16t} {25 (t ^ 2+1)}\\ [4pt]
&=0. \ mwisho {align*}\ nonumber\]

Mwisho, tangu$\vecs r(t)$ inawakilisha curve tatu-dimensional, tunaweza kuhesabu vector binormal kutumia$\ref{EqBinormal}$:

\\ kuanza {align*}\ vecs B (t) &=\;\ vecs T (t) ×\ vecs N (t)\\ [4pt]
&=\ kuanza {vmatrix}\ kofia {i}} &\ kofia {\ hisabati {j}} &\ kofia {\ mathbf {k}}\\ dfrac {3} {5\ sqrt {t ^ 2+1}} & ∙\ dfrac {5t} {5\ sqrt {t ^ 2+1}} & Δ\ dfrac {4} {5\ sqrt {t ^ 2+1}}\ \-\ dfrac {5\ sqrt {t ^ 2+1}} & ∙\ dfrac {5} {5\ sqrt {t ^ 2+1}} &\ drac {4t} {5\ sqrt {t ^ 2+1}}\ mwisho {Matrix}\ [4pt]
& =\ kubwa (\\ kubwa (-\ drac {5t} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kubwa (\ drac {4t)} {5\ sqrt {t ^ 2+1}}\ kubwa) -\ kubwa (-\ drac {4} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kubwa (-\ drac {5} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kubwa)\\ kofia {\ hisabati {i}\
& - kubwa (\ kubwa (\ drac {3} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kubwa (\ drac {4t} {5\ sqrt {t ^ 2+1}}\ kubwa (-\ drac {4} {5\ sqrt {t ^ 2+1}\ kubwa)\ kubwa (-\ drac {3} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kofia {\ hisabati {j}}\\
& +\ kubwa (\ drac {3} {5\ sqrt {t^2+1}}\ kubwa (-\ drac {5} {5\ sqrt {5} rt {t ^ 2+1}}\ kubwa) -\ kubwa (-\ drac {5t} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kubwa (-\ drac {3t} {5\ sqrt {t ^ 2+1}}\ kubwa)\ kofia {k} {k}}\ [4pt]
&=\ kubwa (\ d frac {-20t^2,120} {25 (t ^ 2+1)}\ kubwa)\,\ kofia {i}} +\ kubwa (\ drac {15-15t^2} {25 (t ^ 2+1)}\ kubwa)\,\ kofia {\ hisabati {k}}\\ [4pt]
&= -20\ kubwa (\ dfrac {t ^ 2+1} {25 (t ^ 2+1)}\ kubwa)\,\ kofia {\ hisabati {i}} -15\ kubwa (\ drac {t ^ 2+1} {25 (t ^ 2+1)}\ kubwa)\,\ kofia {k}}\\ [4pt]
&=\\ drac {4} {5}\,\ kofia {\ mathbf {i}} -\ dfrac {3} {5}\,\ kofia {\ mathbf {k}}. \ mwisho {align*}\ nonumber\]

Zoezi$\PageIndex{4}$

Pata kitengo cha kawaida cha vector kwa kazi yenye thamani ya vector$\vecs r(t)=(t^2−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}$ na uitathmini$t=2$.

Kidokezo: Kwanza, tafuta$\vecs T(t)$, kisha utumie$\ref{EqNormal}$.
Jibu: $\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})$

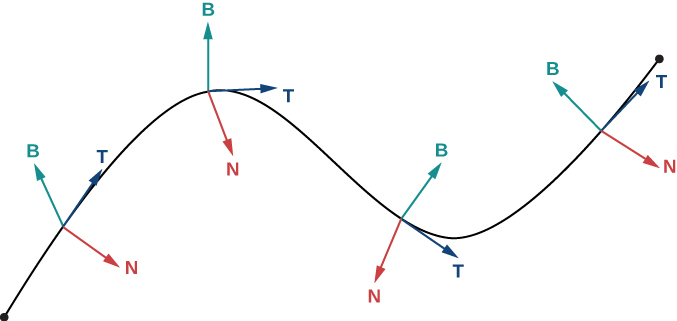
Kwa Curve yoyote laini katika vipimo vitatu kwamba ni defined na kazi vector-thamani, sasa tuna formula kwa kitengo tangent vector$\vecs T$, kitengo kawaida vector$\vecs N$, na vector binormal$\vecs B$. Kitengo cha vector kawaida na vector binormal huunda ndege ambayo ni perpendicular kwa Curve wakati wowote juu ya Curve, inayoitwa ndege ya kawaida. Aidha, wadudu hawa watatu huunda sura ya kumbukumbu katika nafasi tatu-dimensional inayoitwa frame Frenet ya kumbukumbu (pia huitwa sura ya TNB) (Kielelezo$\PageIndex{2}$). Mwisho, ndege kuamua na wadudu$\vecs T$ na$\vecs N$ hufanya ndege osculating ya$C$ wakati wowote$P$ juu ya Curve.

Takwimu hii ni grafu ya kuongezeka kwa kasi na kupungua. Pamoja na pembe katika pointi 4 tofauti ni vectors 3 kila hatua. Vector kwanza inaitwa “T” na ni tangent kwa curve katika hatua. Vector ya pili inaitwa “N” na ni ya kawaida kwa curve katika hatua. Vector ya tatu inaitwa “B” na ni orthogonal kwa T na N. — Kielelezo$\PageIndex{2}$: Takwimu hii inaonyesha sura ya Frenet ya kumbukumbu. Katika kila hatua *$P$juu ya curve tatu-dimensional, kitengo tangent, kitengo kawaida, na vectors binormal kuunda sura tatu-dimensional ya kumbukumbu.*

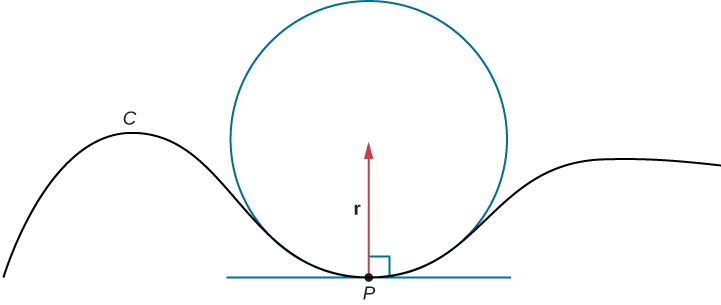
Tuseme sisi fomu mduara katika ndege osculating ya$C$ katika hatua$P$ juu ya Curve. Kudhani kwamba mduara ina curvature sawa na Curve gani katika hatua$P$ na basi mduara na Radius$r$. Kisha, curvature ya mduara hutolewa na$\frac{1}{r}$. Tunaita radius$r$ ya curvature ya curve, na ni sawa na usawa wa curvature. Kama mduara huu uongo upande concave ya Curve na ni tangent kwa Curve katika hatua$P$, basi mduara huu inaitwa osculating mduara wa$C$ saa$P$, kama inavyoonekana katika Kielelezo$\PageIndex{3}$.

Takwimu hii ni grafu ya curve na mduara katikati. Chini ya mduara ni sawa na sehemu ya pembe. Ndani ya mduara ni vector iliyoitwa “r”. Inaanza kwa hatua “P” kwenye mduara na inaelezea kuelekea radius. Pia kuna sehemu ya mstari perpendicular kwa radius na tangent kwa uhakika P. — Kielelezo$\PageIndex{3}$: Katika mduara huu wa osculating, mduara ni tangent kwa curve$C$ katika hatua$P$ *na kushiriki curvature sawa.*

Kwa habari zaidi juu ya mzunguko wa osculating, angalia maandamano haya juu ya curvature na msokoto, makala hii juu ya miduara ya osculating, na mjadala huu wa formula za Serret.

Ili kupata equation ya mzunguko wa osculating katika vipimo viwili, tunahitaji kupata tu kituo na radius ya mduara.

Mfano$\PageIndex{5}$: Finding the Equation of an Osculating Circle

Kupata equation ya mzunguko osculating ya Curve inavyoelezwa na kazi$y=x^3−3x+1$ katika$x=1$.

Suluhisho

Kielelezo$\PageIndex{4}$ inaonyesha grafu ya$y=x^3−3x+1$.

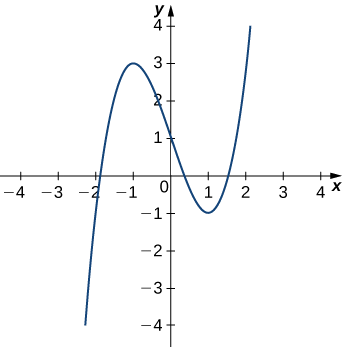
Takwimu hii ni grafu ya kazi ya ujazo y = x ^ 3-3x+1. Curve huongezeka, hufikia kiwango cha juu katika x=-1, hupungua kupitia y axis saa 1, kisha kufikia kiwango cha chini saa x =1 kabla ya kuongezeka tena. — Kielelezo$\PageIndex{4}$: Tunataka kupata mzunguko wa osculating wa grafu hii wakati ambapo$x=1$.

Kwanza, hebu tuhesabu curvature katika$x=1$:

\[κ =\dfrac{|f″(x)|}{\bigg( 1+[f′(x)]^2 \bigg) ^{3/2}} = \dfrac{|6x|}{(1+[3x^2−3]^2)^{3/2}}. \nonumber \]

Hii inatoa$κ=6$. Kwa hiyo, radius ya mzunguko wa osculating hutolewa na$R=\frac{1}{κ}=\dfrac{1}{6}$. Kisha, tunahesabu kuratibu katikati ya mduara. Wakati$x=1$, mteremko wa mstari wa tangent ni sifuri. Kwa hiyo, katikati ya mzunguko wa osculating ni moja kwa moja juu ya hatua kwenye grafu na kuratibu$(1,−1)$. Kituo cha iko katika$(1,−\frac{5}{6})$. Fomu ya mduara na radius$r$ na kituo$(h,k)$ hutolewa na$(x−h)^2+(y−k)^2=r^2$. Kwa hiyo, equation ya mzunguko wa osculating ni$(x−1)^2+(y+\frac{5}{6})^2=\frac{1}{36}$. Grafu na mduara wake wa osculating inaonekana kwenye grafu ifuatayo.

Zoezi$\PageIndex{5}$

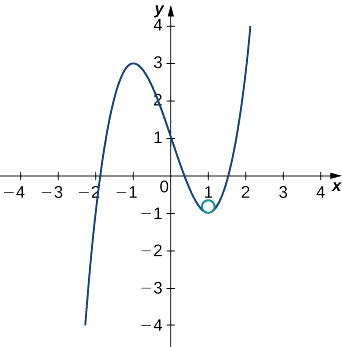
Kupata equation ya mzunguko osculating ya Curve inavyoelezwa na kazi vector-thamani$y=2x^2−4x+5$ katika$x=1$.

Kidokezo: Tumia$\ref{EqK4}$ ili kupata safu ya grafu, kisha futa grafu ya kazi karibu$x=1$ ili kusaidia kutazama mduara kuhusiana na grafu.

Jibu

$κ =\frac{4}{[1+(4x−4)^2]^{3/2}}$

Kwa hatua$x=1$, curvature ni sawa na$4$. Kwa hiyo, radius ya mzunguko wa osculating ni$\frac{1}{4}$.

Grafu ya kazi hii inaonekana ijayo:

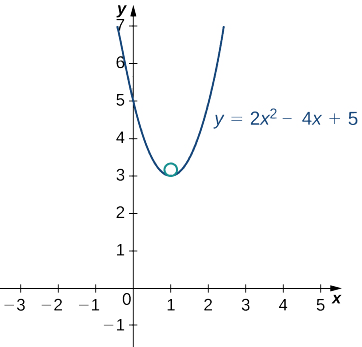
$Takwimu hii ni grafu ya kazi y = 2x ^ 2-4x+5. Curve ni parabola kufungua na vertex katika (1, 3).$

Vertex ya parabola hii iko kwenye hatua$(1,3)$. Zaidi ya hayo, katikati ya mzunguko wa osculating ni moja kwa moja juu ya vertex. Kwa hiyo, kuratibu za kituo ni$(1,\frac{13}{4})$. Equation ya mzunguko wa osculating ni

$(x−1)^2+(y−\frac{13}{4})^2=\frac{1}{16}$.

Dhana muhimu

Kazi ya urefu wa arc kwa kazi yenye thamani ya vector imehesabiwa kwa kutumia formula muhimu$\displaystyle s(t)=\int_a^b ‖\vecs r′(t)‖\,dt $. Fomu hii halali katika vipimo viwili na vitatu.
Curvature ya curve kwa hatua katika vipimo viwili au vitatu hufafanuliwa kuwa curvature ya mduara ulioandikwa wakati huo. Parameterization ya urefu wa arc hutumiwa katika ufafanuzi wa curvature.
Kuna aina mbalimbali za curvature. Upepo wa mduara ni sawa na usawa wa radius yake.
Kitengo kuu vector kawaida katika$t$ hufafanuliwa kuwa
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \nonumber \]
Vector binormal katika$t$ hufafanuliwa kama$\vecs B(t)=\vecs T(t)×\vecs N(t)$,$\vecs T(t)$ wapi kitengo tangent vector.
Frenet sura ya kumbukumbu ni sumu na kitengo tangent vector, kuu kitengo kawaida vector, na binormal vector.
Mduara wa osculating ni tangent kwa curve katika hatua na ina curvature sawa na curve tangent katika hatua hiyo.

Mlinganyo muhimu

Urefu wa safu ya safu ya nafasi
$s= {\displaystyle \int _a^b} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2} \,dt= {\displaystyle \int _a^b} ‖\vecs r′(t)‖\,dt$
Kazi ya urefu wa ARC
$s(t)={\displaystyle \int _a^t} \sqrt{f′(u))^2+(g′(u))^2+(h′(u))^2} \,du \; or \; s(t)={\displaystyle \int _a^t}‖\vecs r′(u)‖\,du$
$κ=\frac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} \; or \; κ=\frac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3} \; or \; κ=\frac{|y″|}{[1+(y′)^2]^{3/2}}$
Kitengo kuu vector kawaida
$\vecs N(t)=\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$
Vector ya kawaida
$\vecs B(t)=\vecs T(t)×\vecs N(t)$

faharasa

kazi ya urefu wa arc: kazi$s(t)$ ambayo inaelezea safu urefu wa Curve$C$ kama kazi ya$t$

parameterization ya urefu wa arc: reparameterization ya kazi yenye thamani ya vector ambayo parameter ni sawa na urefu wa arc

vector ya kawaida: kitengo vector orthogonal kwa kitengo tangent vector na kitengo vector kawaida

mpindo: derivative ya vector kitengo tangent kwa heshima na parameter arc-urefu

Frenet sura ya kumbukumbu: (TNB frame) sura ya kumbukumbu katika nafasi tatu-dimensional sumu na kitengo tangent vector, kitengo vector kawaida, na vector binormal

ndege ya kawaida: ndege ambayo ni perpendicular kwa Curve wakati wowote juu ya Curve

mzunguko wa osculating: mduara kwamba ni tangent kwa Curve$C$ katika hatua$P$ na kwamba hisa curvature huo

osculating ndege: ndege kuamua na tangent kitengo na kitengo vector kawaida

kuu kitengo vector kawaida: orthogonal vector kwa vector kitengo tangent, iliyotolewa na formula$\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$

radius ya curvature: usawa wa curvature

nyororo: curves ambapo kazi vector-thamani$\vecs r(t)$ ni differentiable na derivative yasiyo ya sifuri

Theorem: Arc-Length Formula kwa ndege na nafasi curves

Mfano\(\PageIndex{1}\): Finding the Arc Length

Zoezi\(\PageIndex{1}\)

Theorem: Kazi ya Urefu wa Arc

Mfano\(\PageIndex{2}\): Finding an Arc-Length Parameterization

Zoezi\(\PageIndex{2}\)

Theorem: Njia Mbadala za Curvature

Ushahidi

Mfano\(\PageIndex{3}\): Finding Curvature

Zoezi\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\): Finding the Principal Unit Normal Vector and Binormal Vector

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\): Finding the Equation of an Osculating Circle

Zoezi\(\PageIndex{5}\)