13.2E: Mazoezi ya Sehemu ya 13.2

Last updated
Save as PDF

Page ID: 178330

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Kuchukua derivatives ya Kazi za Vector-Thamani

Katika maswali ya 1 - 10, compute derivative ya kila kazi yenye thamani ya vector.

1)$\vecs r(t)=t^3 \,\hat{\mathbf{i}}+3t^2 \,\hat{\mathbf{j}}+\dfrac{t^3}{6}\,\hat{\mathbf{k}}$

Jibu: $\vecs r'(t)= 3t^2 \,\hat{\mathbf{i}}+6t\,\hat{\mathbf{j}}+\frac{1}{2}t^2\,\hat{\mathbf{k}}$

2)$\vecs r(t)=\sin(t) \,\hat{\mathbf{i}}+\cos(t) \,\hat{\mathbf{j}}+e^t \,\hat{\mathbf{k}}$

3)$\vecs r(t)=e^{−t} \,\hat{\mathbf{i}}+\sin(3t) \,\hat{\mathbf{j}}+10 \sqrt{t} \,\hat{\mathbf{k}}$. Mchoro wa grafu umeonyeshwa hapa. Angalia hali tofauti ya mara kwa mara ya grafu.

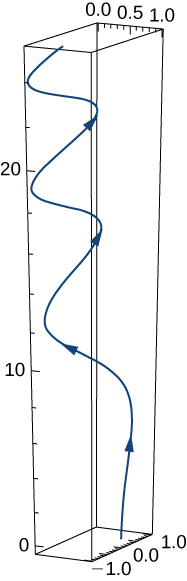
$Grafu ya njia ya mkuta wa 3D ya r (t) =e^ (-t) i + dhambi (3t) j+10 sqrt (t) k.$

Jibu: $\vecs r'(t) = −e^{−t}\,\hat{\mathbf{i}}+3\cos (3t)\,\hat{\mathbf{j}}+\dfrac{5}{\sqrt{t}}\,\hat{\mathbf{k}}$

4)$\vecs r(t)=e^t \,\hat{\mathbf{i}}+2e^t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

5)$\vecs r(t)=\,\hat{\mathbf{i}}+\,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

Jibu: $\vecs r'(t) = ⟨0,0,0⟩ = \vecs 0$

6)$\vecs r(t)=te^t \,\hat{\mathbf{i}}+t \ln(t) \,\hat{\mathbf{j}}+\sin(3t)\,\hat{\mathbf{k}}$

7)$\vecs r(t)=\left\langle\dfrac{1}{t+1},\,\arctan(t), \,\ln t^3 \right\rangle$

Jibu: $\vecs r'(t) = ⟨\dfrac{−1}{(t+1)^2},\dfrac{1}{1+t^2},\dfrac{3}{t}⟩$

8)$\vecs r(t)= \langle\tan 2t, \,\sec 2t, \,\sin ^2 t\rangle$

9)$\vecs r(t)=\langle 3,\, 4 \sin (3t),\, t \cos(t)\rangle$

Jibu: $\vecs r'(t) = ⟨0,12 \cos(3t), \cos t−t \sin t⟩$

10)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+te^{−2t} \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

Eleza na mchoro Curve iliyowakilishwa na kazi yenye thamani ya vector$\vecs r(t)=⟨6t,6t−t^2⟩$.

pata uhakika juu ya Curve$\vecs r(t)=⟨6t,6t−t^2⟩$ na kutoa thamani ya kazi katika hatua hii.

Jibu: b.$\vecs r(t)=⟨18,9⟩$ katika$ t=3$

12) Pata equations parametric ya mstari tangent kwa Curve$\vecs r(t)=⟨t, t^2,t⟩$ saa$t=2$.

13) Pata equations parametric ya mstari tangent kwa Curve$\vecs r(t)=⟨e^t,e^{−t},0⟩$ saa$t=0$.

Jibu: $x=1+t,\quad y=1−t,\quad z=0$

14) Compute kwanza, pili, na derivatives ya tatu ya$\vecs r(t)=3t \,\hat{\mathbf{i}}+6\ln(t) \,\hat{\mathbf{j}}+5e^{−3t}\,\hat{\mathbf{k}}$.

Kuelezea Mwendo na Kazi za Vector-Thamani

Katika maswali 15 - 17, pata kasi na kuongeza kasi kwa nyakati zilizopewa, njama grafu ya kazi ya msimamo, na kuteka katika vectors kasi na kasi katika maeneo yanayofanana kwenye safu.

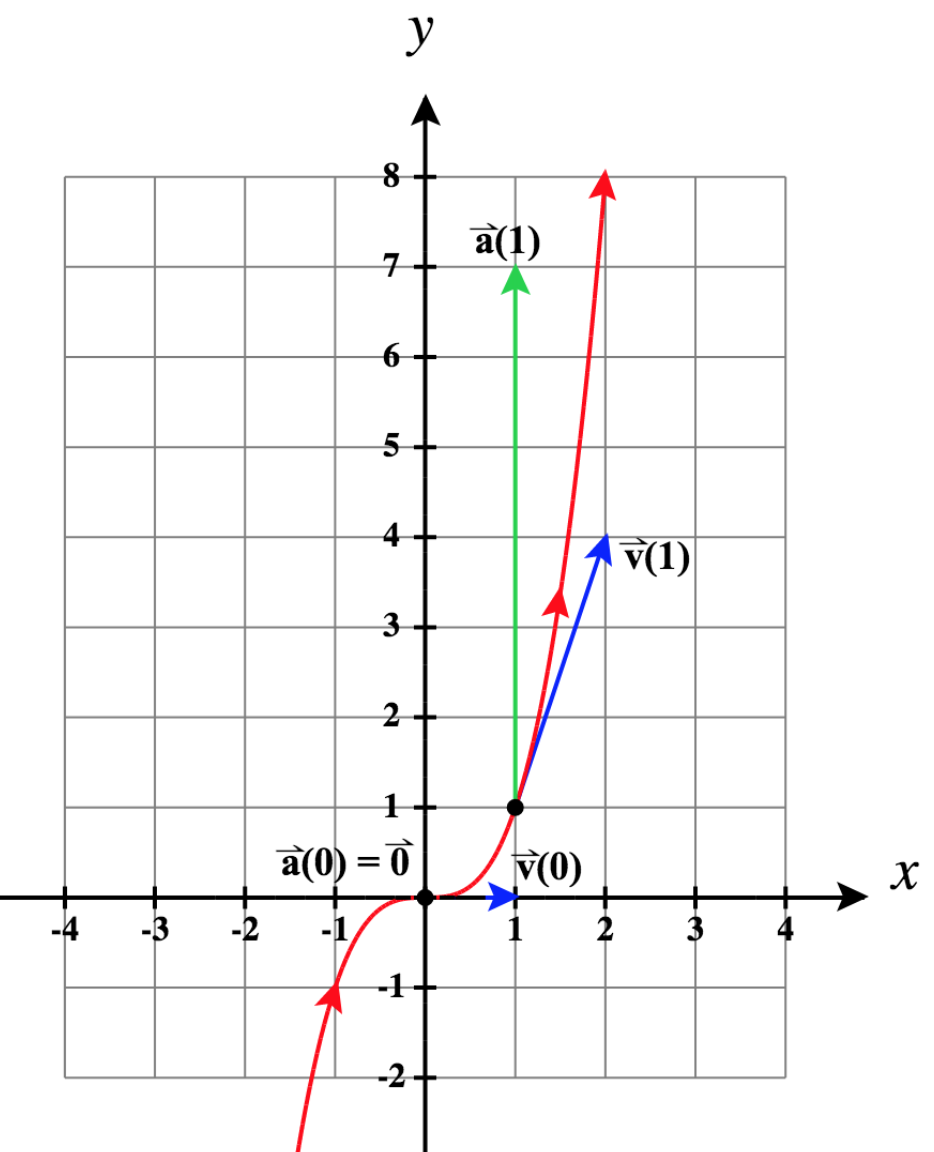
15)$\vecs r(t)= t \,\hat{\mathbf{i}}+t^3\,\hat{\mathbf{j}}$, saa$t = 0$ na$t = 1$

Jibu: \ (\ kuanza {safu} {lll}\, & t = 0: & t = 1:\
\ vecs r (t) = t\,\ mathbf {\ kofia i} + t ^ 3\,\ mathbf {\ kofia j}, &\ vecs r (0) =\ vecs 0, &\ vecs r (1) =\ mathbf {\ kofia i} +\ mathbf {\ kofia j}\
\ vecs v (t) =\ mathbf {\ kofia i} + 3t ^ 2\,\ mathbf {\ kofia j}, &\ vecs v (0) =\ mathbf {\ kofia i}, &\ vecs v (1) =\ mathbf {\ kofia i} + 3\,\ mathbf {\ kofia j}\
\ vecs (t) = 6t\,\ mathbf {\ kofia j}, &\ vecs (0) =\ vecs 0, &\ vecs a (1) = 6\,\ mathbf {\ kofia j}\ mwisho {safu}\)
$Njia pamoja na graph ya y = x ^ 3 kutoka kushoto-kulia. Pia kuonyesha kasi na kuongeza kasi wadudu katika t = 0 na t = 1.$

16)$\vecs r(t)= \cos t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}}$, katika$t = 0$, katika$t = \frac{\pi}{4}$, na$t = \frac{\pi}{2}$

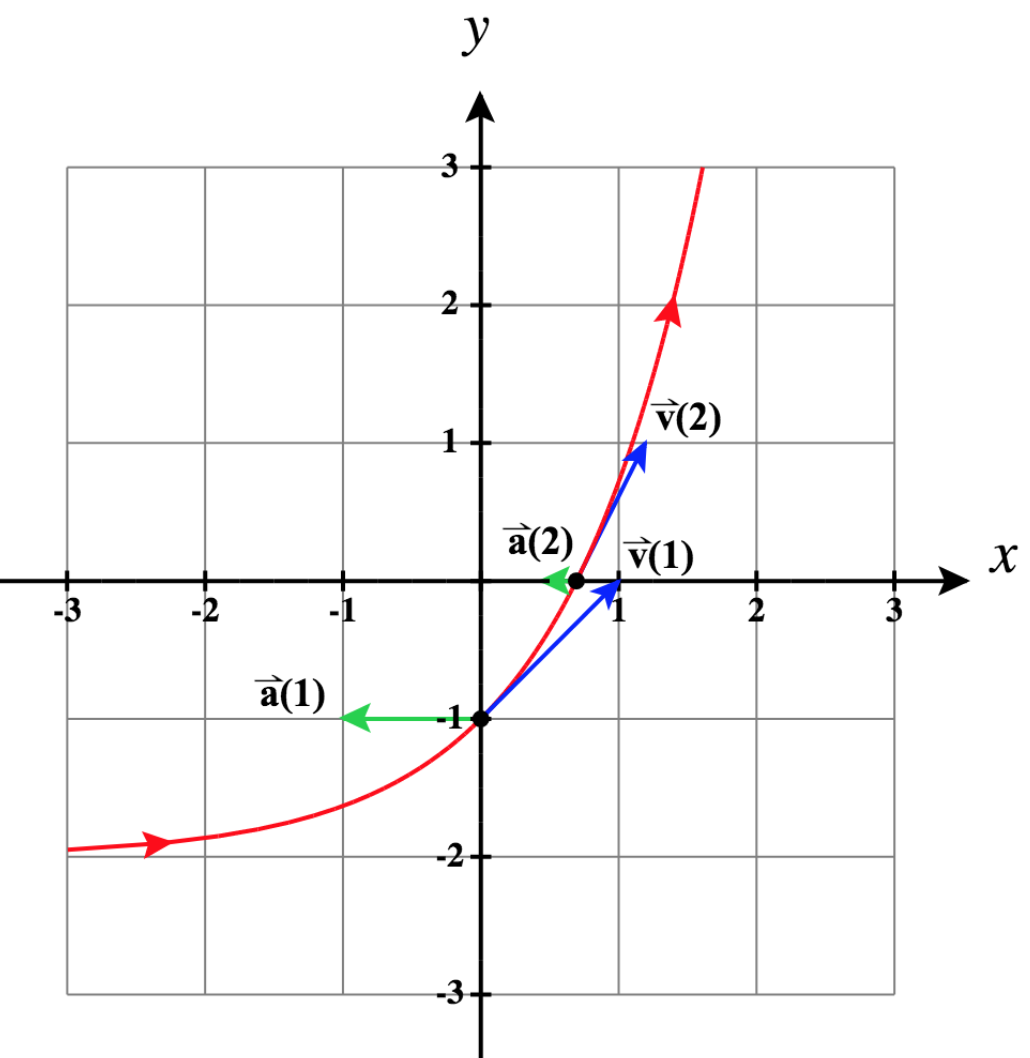
17)$\vecs r(t)= \ln t \,\hat{\mathbf{i}}+(t-2)\,\hat{\mathbf{j}}$, saa$t = 1$ na$t = 2$

Jibu: \ (\ kuanza {safu} {lll}\, & t = 1: & t =2:\
\ vecs r (t) = (\ ln t)\,\ mathbf {\ kofia i} + (t - 2)\,\ mathbf {\ kofia j}, &\ vecs r (1) = -\ mathbf {\ kofia j}, &\ vecs r (2) = (\ ln 2)\,\ mathbf {\ kofia i}\
\ vecs v (t) =\ dfrac {1} {t}\,\ mathbf {\ kofia i} +\ mathbf {\ kofia j}, &\ vecs v (1) =\ mathbf {\ kofia i} +\ mathbf {\ kofia j}, &\ vecs v (2) =\ frac {1} {2}\ mathbf {\ kofia i} +\ hatbf {\ kofia j}\
\ vecs a (t) = -\ dfrac {1}} {t ^ 2}\\ mathbf {\ kofia i}, &\ vecs a (1) = -\ mathbf {\ kofia i}, &\ vecs a (2) = -\ frac {1} {4}\,\ mathbf {\ kofia i}\ mwisho {safu}\)
$Njia pamoja na grafu ya r (t) = ln (t) i + (t - 2) j Pia kuonyesha kasi na kuongeza kasi wadudu katika t = 1 na t = 2.$

Katika maswali 18 - 24, pata kasi, kasi, na kasi ya chembe na kazi iliyopewa nafasi. Kumbuka kwamba kasi ni ukubwa wa kasi iliyowakilishwa na$‖\vecs v(t)‖$ au$‖\vecs r′(t)‖$.

18)$\vecs r(t)=e^{2t} \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$

19)$\vecs r(t)=\cos t^3 \,\hat{\mathbf{i}}+\sin t^3 \,\hat{\mathbf{j}}$

Jibu: $\vecs v(t)=-3t^2\sin t^3 \,\hat{\mathbf{i}}+3t^2\cos t^3 \,\hat{\mathbf{j}}, \quad \text{speed}(t)=‖\vecs v(t)‖=3t^2, \quad \vecs a(t) = \left( -6t\sin t^3 - 9t^4\cos t^3 \right) \,\hat{\mathbf{i}}+\left( 6t\cos t^3 - 9t^4\sin t^3 \right) \,\hat{\mathbf{j}}$

20)$\vecs r(t)=⟨e^t,e^{−t},0⟩$

21)$\vecs r(t)=⟨t+ \cos t,t− \sin t⟩$

Jibu: $\vecs v(t)=⟨1− \sin t,1−\cos t⟩, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{3−2( \sin t+\cos t)}, \quad \vecs a(t) = ⟨- \cos t, \sin t⟩$

22)$\vecs r(t)=\dfrac{2t−1}{2t+1} \,\hat{\mathbf{i}}+\ln(1−4t^2) \,\hat{\mathbf{j}}$

23)$\vecs r(t)=\cos 3t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}} + 0.5t \,\hat{\mathbf{k}} $

Jibu: $\vecs v(t)=-3\sin 3t \,\hat{\mathbf{i}}+3\cos 3t \,\hat{\mathbf{j}} +0.5 \,\mathbf{\hat k}, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{9.25}\text{ units/sec}, \quad \vecs a(t) = -9\cos 3t \,\hat{\mathbf{i}}-9\sin 3t \,\hat{\mathbf{j}}$

24)$\vecs r(t)=e^{-t} \,\hat{\mathbf{i}}+(\ln t) \,\hat{\mathbf{j}}+(\sin 7t)\,\hat{\mathbf{k}}$

25) Fikiria vector msimamo kwa chembe kuwa$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$. Grafu inavyoonyeshwa hapa:

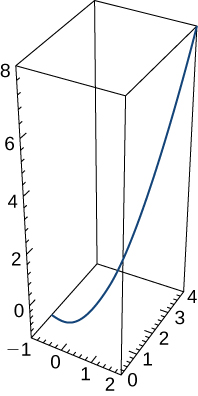
Kupata vector kasi wakati wowote.

pata kasi ya chembe wakati wa$t=2$ sec.

c Kupata kasi kwa wakati$t=2$ sec.

Jibu: a.$\vecs v(t)=\hat{\mathbf{i}}+2t\,\hat{\mathbf{j}}+3t^2 \,\hat{\mathbf{k}}$
b.$\sqrt{161}$ vitengo/sec
Kumbuka kuwa$\text{speed}(t) = \|\vecs v(t)\| = \sqrt{1^2 + (2t)^2 + (3t^2)^2} = \sqrt{1 + 4t^2 + 9t^4}.$
Hivyo,$\text{speed}(2) = \sqrt{1 + 16 + 9(16)} = \sqrt{161}$ vitengo/sec.
c Tangu$\vecs a(t)=2\,\hat{\mathbf{j}}+6t \,\hat{\mathbf{k}},$$\vecs a(2) = 2\,\hat{\mathbf{j}}+12 \,\hat{\mathbf{k}}$

26) Chembe husafiri kando ya njia ya duaradufu na equation$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Pata zifuatazo:

a. kasi ya chembe

Jibu: $\vecs v(t)=⟨−\sin t,2 \cos t,0⟩$

b Kasi ya chembe$t=\frac{π}{4}$

c. kuongeza kasi ya chembe$t=\frac{π}{4}$

Jibu: $\vecs a(t)=⟨−\frac{\sqrt{2}}{2},−\sqrt{2},0⟩$

27) Onyesha kwamba ikiwa kasi ya chembe inayosafiri kando ya pembe iliyowakilishwa na kazi yenye thamani ya vector ni mara kwa mara, basi kazi ya kasi ni daima perpendicular kwa kazi ya kuongeza kasi.

Jibu: $\begin{align*} ‖\vecs v(t)‖ \; & = k \\ \vecs v(t)·\vecs v(t) \; & = k^2 \\ \frac{d}{dt}\Big(\vecs v(t)·\vecs v(t)\Big) \; & =\frac{d}{dt}\Big(k^2\Big)=0 \\ \vecs v(t)·\vecs v′(t)+\vecs v′(t)·\vecs v(t) \; & = 0 \\ 2\vecs v(t)·\vecs v′(t) \; & =0 \\ \vecs v(t)·\vecs v′(t) \; & = 0\end{align*}$

Taarifa ya mwisho ina maana kwamba kasi na kasi ni perpendicular au orthogonal.

28) Kutokana na kazi yenye thamani ya vector$\vecs r(t)=⟨\tan t,\sec t,0⟩$ (grafu inavyoonyeshwa hapa), tafuta zifuatazo:

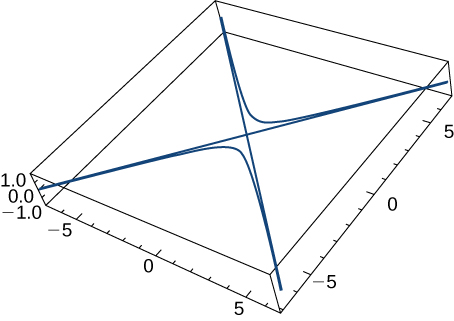
a. kasi

Jibu: $\vecs v(t)=\langle \sec ^2 t,\,\sec t \tan t\rangle$

b Kasi

Jibu: $‖\vecs v(t)‖=\sqrt{\sec ^4 t+\sec ^2 t \tan ^2 t}=\sqrt{(\sec ^2 t)(\sec ^2 t+\tan ^2 t)}$

c Kuharakisha

Jibu: $\vecs a(t)=\langle 2\sec ^2 t\tan t,\,\sec t \tan^2 t+\sec^3 t\rangle$

29) Kupata kasi ya chini ya chembe kusafiri pamoja Curve$\vecs r(t)=⟨t+\cos t,t−\sin t⟩$, ambapo$t∈[0,2π)$. Kisha pia kupata kasi yake ya juu wakati huu.

Jibu: Min. kasi ni$\sqrt{3-2\sqrt{2}}\approx 0.41421$ wakati$t=\tfrac{\pi}{4}$.
Max. kasi ni$\sqrt{3+2\sqrt{2}}\approx 2.41421$ wakati$t=\tfrac{5\pi}{4}$.

Kwa maswali 30 - 31, fikiria chembe inayoendelea kwenye njia ya mviringo ya radius$b$ kulingana na kazi$\vecs r(t)=b \cos(\omega t) \,\hat{\mathbf{i}}+b\sin(\omega t) \,\hat{\mathbf{j}}$,$\omega$ wapi kasi ya angular,$\dfrac{d \theta}{dt}$.

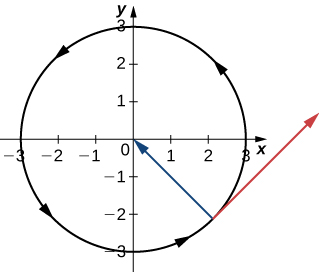
30) Onyesha kwamba kasi ya chembe ni sawa na kasi ya angular.

31) Kupata kasi kazi na kuonyesha kwamba$\vecs v(t)$ daima orthogonal kwa$\vecs r(t)$.

Jibu: $\vecs r'(t)=−b \omega \sin( \omega t)\,\hat{\mathbf{i}}+b \omega \cos(\omega t)\,\hat{\mathbf{j}}$. Ili kuonyesha orthogonality, kumbuka kuwa$\vecs r'(t)⋅\vecs r(t)=0$.

Urahisi wa Kazi za Vector-Thamani

Kwa maswali 32 - 40,

a Kuamua maadili yoyote ambayo$\vecs r$ si laini.$t$

b Kuamua vipindi vya wazi ambavyo$\vecs r$ ni laini.

c Graph kazi ya thamani ya vector na kuelezea tabia yake katika maeneo ambayo si laini.

32)$\vecs r(t) = \langle 3t, 5t^2 - 1\rangle$

33)$\vecs r(t)= t^3\,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}$

Jibu: a.$\vecs r$ si laini katika$t = 0$, tangu$\vecs r'(0) = \vecs 0$.
b.$\vecs r$ ni laini juu ya vipindi wazi$(-\infty, 0)$ na$(0, \infty)$.
c. kuna cusp wakati$t = 0$.

34)$\vecs r(t)=\langle 5,\, 2 \sin (t),\, \cos(t)\rangle$

35)$\vecs r(t) = \langle t^3 - 3t^2, 7\rangle$

Jibu: a.$\vecs r$ si laini katika$t = 0$ na$t = 2$, tangu$\vecs r'(0) = \vecs 0$ na$\vecs r'(2) = \vecs 0$.
b.$\vecs r$ ni laini juu ya vipindi wazi$(-\infty, 0)$,$(0, 2)$, na$(2, \infty)$.
c. mwendo juu ya Curve reverses katika njia moja katika wote$t = 0$ na$t = 2$.

36)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+t^3 \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

37)$\vecs r(t)=\left\langle \ln(t^2+4t+5), \,\dfrac{t^3}{3} - 4t,\, 5\right\rangle$

Jibu: a.$\vecs r$ si laini katika$t = -2$, tangu$\vecs r'(-2) = \vecs 0$.
Tangu uwanja wa$\vecs r$ sisi$(-\infty, \infty)$, hii ni yote tunapaswa kuondoa.
b.$\vecs r$ ni laini juu ya vipindi wazi$(-\infty, -2)$ na$(-2, \infty)$.
c. kuna cusp wakati$t = -2$.

38)$\vecs r(t) = \left( 5\cos t - \cos 5t\right) \,\hat{\mathbf{i}} + \left( 5\sin t - \sin 5t \right) \,\hat{\mathbf{j}}$, kwa$0 \le t \le 2\pi$

39)$\vecs r(t)=\sqrt{t^3 + 9t^2} \,\hat{\mathbf{i}}+\left(t^2 +12t\right) \,\hat{\mathbf{j}}+7\,\hat{\mathbf{k}}$

Jibu: a. uwanja wa$\vecs r$ ni$[-9, \infty)$.
Na$\vecs r$ si laini katika$t = -6$, tangu$\vecs r'(-6) = \vecs 0$.
uwanja wa sisi$\vecs r'$$(-9, \infty)$, tangu$\vecs r'$ haijulikani katika$t = -9$.
b.$\vecs r$ ni laini juu ya vipindi wazi$(-9, -6)$ na$(-6, \infty)$.
c. kuna cusp wakati$t = -6$.

40)$\vecs r(t)= \cos^3 t\,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$, kwa$0 \le t \le 2\pi$

Jibu: a. uwanja wa$\vecs r$ ni$(-\infty, \infty)$.
$\vecs r'(t) = -3(\cos^2 t)(\sin t)\,\hat{\mathbf{i}}+\cos t \,\hat{\mathbf{j}}$. Ni uwanja pia$(-\infty, \infty)$.
Lakini kumbuka kuwa vipengele vyote vina sababu ya$\cos t$, hivyo vipengele vyote viwili vitakuwa$0$ wakati$\cos t = 0$.
Kwa hiyo,$\vecs r$ si laini katika$t = \frac{\pi}{2}$ na wakati$t = \frac{3\pi}{2}$, tangu$\vecs r'\left( \frac{\pi}{2}\right) = \vecs 0$ na$\vecs r'\left( \frac{3\pi}{2}\right) = \vecs 0$. Kumbuka basi kwamba$\vecs r$ si laini kwa nyingi yoyote isiyo ya kawaida ya$\frac{\pi}{2}$, yaani$t = \frac{(2n + 1)\pi}{2}$, kwa thamani yoyote integer$n$.
b.$\vecs r$ ni laini juu ya vipindi wazi$\left(\dfrac{(2n - 1)\pi}{2}, \dfrac{(2n + 1)\pi}{2}\right)$, kwa thamani yoyote integer$n$.
c. kuna cusp wakati$t = \dfrac{(2n + 1)\pi}{2}$, kwa thamani yoyote integer$n$.

Mali ya derivative

Kwa maswali, 41-43, tathmini kila kujieleza kutokana$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}−t^4 \,\hat{\mathbf{k}} $ na kwamba na$\vecs s(t)=\sin(t) \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+ \cos(t) \,\hat{\mathbf{k}} $

41)$\dfrac{d}{dt}\big[\vecs r(t^2)\big]$

Jibu: $\dfrac{d}{dt}\big[\vecs r(t^2)\big] = ⟨2t,4t^3,−8t^7⟩$

42)$\dfrac{d}{dt}\big[t^2⋅\vecs s(t)\big]$

43)$\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]$

Jibu: $\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]=\sin t+2te^t−4t^3 \cos t+t\cos t+t^2e^t+t^4\sin t$

44) Kupata$\vecs r'(t)⋅\vecs r''(t) \; for \; \vecs r(t)=−3t^5 \,\hat{\mathbf{i}}+5t \,\hat{\mathbf{j}}+2t^2 \,\hat{\mathbf{k}}$.

Jibu: $\vecs r'(t)⋅\vecs r''(t) = 900t^7+16t$

45) Kutokana$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$ na$\vecs u(t)=4t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$, kupata$\frac{d}{dt}(\vecs r(t) \times \vecs u(t))$.

46) Tathmini$\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big]$ iliyotolewa$\vecs u(t)=t^2 \,\hat{\mathbf{i}}−2t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

Jibu: $\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big] = 0 \,\hat{\mathbf{i}} +2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}$

47) Kutokana$\vecs r(t)=t \,\hat{\mathbf{i}}+2\sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$ na$\vecs u(t)=\dfrac{1}{t} \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$, kupata zifuatazo:

a.$\vecs r(t) \times \vecs u(t)$

Jibu: $\vecs r(t) \times \vecs u(t) = \left\langle 0, \;2(\cos t)\left(\frac{1}{t}-t\right),\; 2 (\sin t)\left(t- \frac{1}{t}\right)\right\rangle$

b.$\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big)$

Jibu: $\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big) = \left\langle 0, \;2(\sin t)\left(t− \frac{1}{t}\right)−2 (\cos t)\left(1+ \frac{1}{t^2}\right),\;2 \left(\sin t\right)\left(1+ \frac{1}{t^2}\right)+2 \left(\cos t\right)\left(t−\frac{1}{t}\right)\right\rangle$

c Sasa, tumia utawala wa bidhaa kwa derivative ya bidhaa ya msalaba wa wadudu wawili na kuonyesha matokeo haya ni sawa na jibu la tatizo lililotangulia.

kitengo Tangent wadudu

Kwa maswali 48 - 51, tafuta kitengo cha tangent vector kwa thamani iliyoonyeshwa ya$t$.

48)$\vecs r(t)=3t^3 \,\hat{\mathbf{i}}+2t^2 \,\hat{\mathbf{j}}+\dfrac{1}{t} \,\hat{\mathbf{k}}; \quad t=1$

49)$\vecs r(t)=t \,\hat{\mathbf{i}}+\sin(2t) \,\hat{\mathbf{j}}+\cos(3t) \,\hat{\mathbf{k}}; \quad t=\frac{π}{3}$

Jibu: $\vecs r'\left(\frac{π}{3}\right) = \langle 1, \,-1,0\rangle$ni vector tangent, hivyo kitengo tangent vector itakuwa:
$\frac{1}{\sqrt{2}}⟨1,−1,0⟩ \quad = \quad \langle \frac{\sqrt{2}}{2}, \,-\frac{\sqrt{2}}{2},\, 0\rangle$

50)$\vecs r(t)=\cos(2t) \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}};\quad t=\frac{π}{2}$

51)$\vecs r(t)=3e^t \,\hat{\mathbf{i}}+2e^{−3t} \,\hat{\mathbf{j}}+4e^{2t} \,\hat{\mathbf{k}}; \quad t= \ln(2)$

Jibu: $\vecs r'(\ln(2))= ⟨6,−\frac{3}{4},32⟩$ni vector tangent, hivyo kitengo tangent vector itakuwa:
$\dfrac{1}{\sqrt{1060.5625}}\left\langle 6,−\frac{3}{4},32\right\rangle \quad = \quad \left\langle \dfrac{24\sqrt{16969}}{16969}, -\dfrac{12\sqrt{16969}}{67876}, \frac{128\sqrt{16969}}{16969}\right\rangle$

Kwa maswali 52 - 58, tafuta kitengo cha tangent vector$\vecs T(t)$ kwa curves zifuatazo parameterized.

52)$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$

53)$\vecs r(t)=6 \,\hat{\mathbf{i}}+\cos(3t) \,\hat{\mathbf{j}}+3\sin(4t) \,\hat{\mathbf{k}}, \quad 0≤t<2π$

Jibu: $\vecs T(t)=\dfrac{1}{\sqrt{9\sin ^2 (3t)+144\cos ^2 (4t)}}⟨0,−3\sin(3t),12\cos(4t)⟩$

54)$\vecs r(t)=⟨t \cos t,t \sin t⟩$

55)$\vecs r(t)=⟨t+1,2t+1,2t+2⟩$

Jibu: $\vecs T(t)=\frac{1}{3} ⟨1,2,2⟩$

56)$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+\sin t \,\hat{\mathbf{k}}, \quad 0≤t<2π$. Maoni mawili ya pembe hii yanawasilishwa hapa:

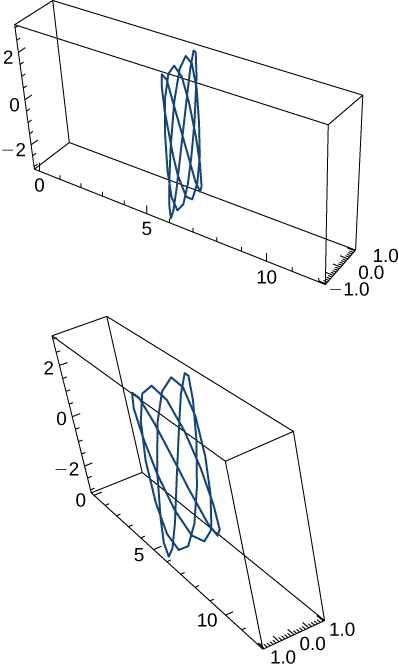
57)$\vecs r(t)=\left\langle t,\dfrac{1}{t}\right\rangle$. Grafu inavyoonyeshwa hapa:

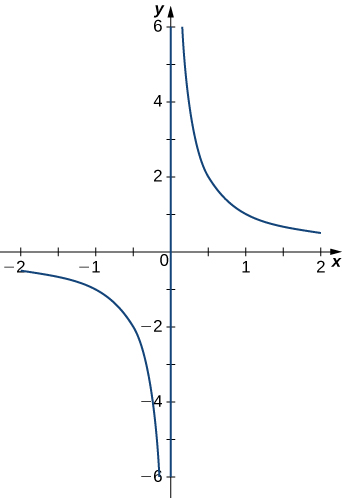
Jibu: $\vecs T(t)=\left\langle\dfrac{t^2}{\sqrt{t^4+1}},\frac{-1}{\sqrt{t^4+1}}\right\rangle$

58)$\vecs r(t)=3 \cos(4t) \,\hat{\mathbf{i}}+3 \sin(4t) \,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}},\quad 1 \le t \le 2$

Jibu: $\vecs T(t)=−\frac{12}{13} \sin(4t) \,\hat{\mathbf{i}}+ \frac{12}{13}\cos (4t) \,\hat{\mathbf{j}}+\frac{5}{13} \,\hat{\mathbf{k}}$

59) Chembe husafiri kando ya njia ya helix na equation$\vecs r(t)= \cos(t) \,\hat{\mathbf{i}}+\sin(t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}$. Angalia grafu iliyotolewa hapa:

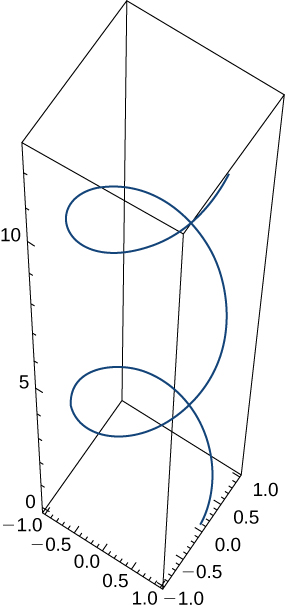
Pata zifuatazo:

a. kasi ya chembe wakati wowote

Jibu: $\vecs v(t)=⟨−\sin t,\cos t,1⟩$

b Kasi ya chembe wakati wowote

c. kuongeza kasi ya chembe wakati wowote

Jibu: $\vecs a(t)=−\cos t \,\hat{\mathbf{i}}− \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$

d. kupata kitengo tangent vector kwa helix.

Ushirikiano wa Kazi za Vector-Thamani

Tathmini integrals zifuatazo:

60)$\displaystyle \int \left(e^t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+ \frac{1}{2t−1} \,\hat{\mathbf{k}}\right)\, dt$

61)$\displaystyle \int_0^1 \vecs r(t)\,dt$, wapi$\vecs r(t)=\left\langle\sqrt[3]{t},\dfrac{1}{t+1},e^{−t}\right\rangle$

Jibu: $\frac{3}{4}\,\hat{\mathbf{i}}+\ln(2) \,\hat{\mathbf{j}}+(1−\frac{1}{e}) \,\hat{\mathbf{k}}$

62) Tathmini$\displaystyle \int_0^3‖t\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}‖dt$.

Jibu: $\frac{1}{3}(10^{\frac{3}{2}}−1)$

63) Kazi ya kuongeza kasi, kasi ya awali, na nafasi ya awali ya chembe ni

\[\begin{align*} \vecs a(t)&=−5 \cos t \,\hat{\mathbf{i}}−5\sin t \,\hat{\mathbf{j}}, \\ \vecs v(0)&=9 \,\hat{\mathbf{i}}+2 \,\hat{\mathbf{j}}, \quad \text{and} \\ \vecs r(0)&=5 \,\hat{\mathbf{i}} \end{align*}\]

Kupata$\vecs v(t)$ na$\vecs r(t)$.

Jibu: $\vecs v(t) = \left(9 - 5\sin t\right)\,\hat{\mathbf{i}} + \left(-3 + 5\cos t\right)\,\hat{\mathbf{j}}$
$\vecs r(t) = \left(9t + 5\cos t\right)\,\hat{\mathbf{i}} + \left(-3t + 5\sin t\right)\,\hat{\mathbf{j}}$

64) Kupata antiderivative ya$\vecs r'(t)=\cos(2t) \,\hat{\mathbf{i}}−2\sin t \,\hat{\mathbf{j}}+\dfrac{1}{1+t^2} \,\hat{\mathbf{k}}$ kwamba satisfies hali ya awali$\vecs r(0)=3 \,\hat{\mathbf{i}}−2 \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

65) kitu huanza kutoka mapumziko katika hatua$P(1,2,0)$ na hatua na kuongeza kasi ya$\vecs a(t)=\,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}}$, ambapo$‖\vecs a(t)‖$ ni kipimo kwa miguu kwa pili kwa sekunde. Pata eneo la kitu baada ya$t=2$ sec.

Wachangiaji:

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created questions 11 - 19.