13.4: Mwendo katika nafasi

Malengo ya kujifunza

• Eleza vectors kasi na kuongeza kasi ya chembe kusonga katika nafasi.
• Eleza vipengele vya tangential na vya kawaida vya kuongeza kasi.
• Sheria za hali ya Kepler ya mwendo wa sayari.

Sasa tumeona jinsi ya kuelezea curves katika ndege na katika nafasi, na jinsi ya kuamua mali zao, kama urefu wa arc na curvature. Yote hii inasababisha lengo kuu la sura hii, ambayo ni maelezo ya mwendo pamoja na curves za ndege na curves za nafasi. Sasa tuna zana zote tunazohitaji; katika sehemu hii, tunaweka mawazo haya pamoja na kuangalia jinsi ya kuitumia.

Vectors Motion katika Ndege na katika nafasi

Hatua yetu ya mwanzo ni kutumia kazi za thamani ya vector ili kuwakilisha nafasi ya kitu kama kazi ya wakati. Nyenzo zote zifuatazo zinaweza kutumika ama kwa curves katika ndege au kwa curves nafasi. Kwa mfano, tunapoangalia obiti ya sayari, curves zinazofafanua njia hizi zote ziko katika ndege kwa sababu ni elliptical. Hata hivyo, chembe inayosafiri kando ya helix inakwenda kwenye pembe katika vipimo vitatu.

Ufafanuzi: Kasi, kasi, na Kuharakisha

Hebu\(\vecs r(t)\) iwe kazi ya vector yenye thamani ya mara mbili ya parameter\(t\) ambayo inawakilisha nafasi ya kitu kama kazi ya wakati.

Vector kasi\(\vecs v(t)\) ya kitu hutolewa na

\[\text{Velocity}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]

Vector kuongeza kasi\(\vecs a(t)\) hufafanuliwa kuwa

\[\text{Acceleration}\,=\vecs a(t)=\vecs v′(t)=\vecs r″(t). \label{Eq2} \]

Kasi hufafanuliwa kuwa

\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]

Kwa kuwa\(\vecs{r}(t)\) inaweza kuwa katika vipimo viwili au vitatu, kazi hizi za thamani ya vector zinaweza kuwa na vipengele viwili au vitatu. Katika vipimo viwili, tunafafanua\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) na katika vipimo vitatu\(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Kisha kasi, kasi, na kasi inaweza kuandikwa kama inavyoonekana katika meza ifuatayo.

Jedwali\(\PageIndex{1}\): Fomu za Msimamo, Kasi, Kuharakisha, na Kasi

Wingi	Vipimo viwili	Vipimo vitatu
Nafasi	\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\)	\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\)
Kasi	\(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}\)	\(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}+z′(t) \hat{\mathbf k}\)
Kuharakisha	\(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}\)	\(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}+z″(t) \hat{\mathbf k}\)
Kasi	\(\|\vecs{v}(t)\|= \sqrt{(x′(t))^2+(y′(t))^2}\)	\(\|\vecs{v}(t)\|=\sqrt{(x′(t))^2+(y′(t))^2+(z′(t))^2}\)

Mfano\(\PageIndex{1}\): Studying Motion Along a Parabola

chembe hatua katika njia parabolic inavyoelezwa na kazi vector-thamani\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), ambapo\(t\) hatua muda katika sekunde.

1. Kupata kasi, kuongeza kasi, na kasi kama kazi ya muda.
2. Mchoro Curve pamoja na vector kasi kwa wakati\(t=1\).

Suluhisho

1. Tunatumia Ulinganyo\ ref {Eq1},\ ref {Eq2}, na\ ref {Eq3}:

   \[ \begin{align*} \vecs{v}(t) &= \vecs{r}′(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}′(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}′(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]

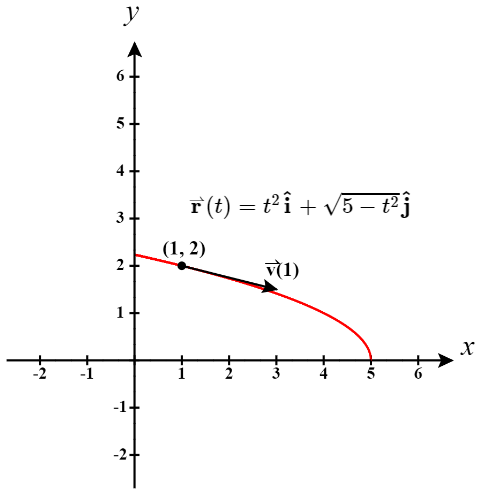
2. Grafu ya\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) ni sehemu ya parabola (Kielelezo\(\PageIndex{1}\)).
   
   Wakati\(t=1\),\(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
   
   Hivyo chembe itakuwa iko katika hatua\((1, 2)\) wakati\(t =1\).
   
   Vector kasi katika\(t=1\) ni

   \[ \begin{align*} \vecs{v}(1) &=\vecs{r}′(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]

   na vector kuongeza kasi katika\(t=1\) ni

   \[\vecs{a}(1)=\vecs{v}′(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]

   Angalia kwamba vector kasi ni tangent kwa njia, kama ilivyo kawaida.

Kielelezo\(\PageIndex{1}\): Grafu hii inaonyesha vector kasi\(t=1\) kwa wakati kwa chembe kusonga katika njia parabolic.

Zoezi\(\PageIndex{1}\)

Chembe huenda katika njia inayofafanuliwa na kazi yenye thamani ya vector\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), ambapo\(t\) hupima muda kwa sekunde na ambapo umbali hupimwa kwa miguu. Kupata kasi, kuongeza kasi, na kasi kama kazi ya muda.

Kidokezo

Tumia Ulinganyo\ ref {Eq1},\ ref {Eq2}, na\ ref {Eq3}.

Jibu

\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\]

\[ ||\vecs{r}′(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]

Vitengo vya kasi na kasi ni miguu kwa pili, na vitengo vya kuongeza kasi ni miguu kwa mraba wa pili.

Ili kupata ufahamu bora wa vectors kasi na kasi, fikiria unaendesha gari kando ya barabara. Ikiwa hugeuka usukani, ungeendelea kwenye mstari wa moja kwa moja na kukimbia barabara. kasi ambayo wewe ni kusafiri wakati kukimbia mbali ya barabara, pamoja na mwelekeo, anatoa vector anayewakilisha kasi yako, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\): Katika kila hatua kando ya barabara iliyosafiri na gari, vector kasi ya gari ni tangent kwa njia iliyosafiri na gari.

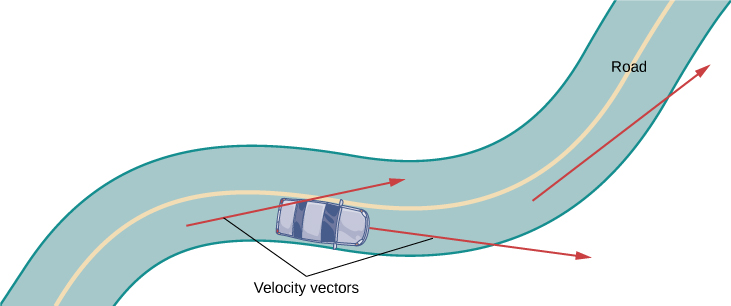
Hata hivyo, ukweli kwamba lazima ugeuke usukani ili uendelee barabara inaonyesha kwamba kasi yako inabadilika (hata kama kasi yako sio) kwa sababu mwelekeo wako unabadilika daima kukuweka barabara. Unapogeuka upande wa kulia, vector yako ya kuongeza kasi pia inaonyesha haki. Unapogeuka upande wa kushoto, vector yako ya kuongeza kasi inaelezea upande wa kushoto. Hii inaonyesha kwamba kasi yako na kuongeza kasi vectors ni kubadilika, bila kujali kama kasi yako halisi inatofautiana (Kielelezo\(\PageIndex{3}\)).

Kielelezo\(\PageIndex{3}\): Mstari uliopigwa unawakilisha trajectory ya kitu (gari, kwa mfano). Vector kasi inaonyesha kuelekea ndani ya upande wakati wote.

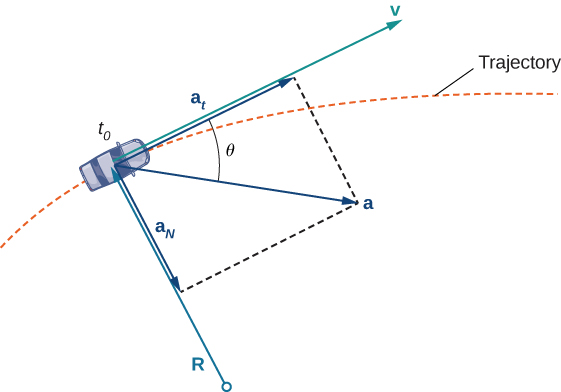
Vipengele vya Vector ya Kuharakisha

Tunaweza kuchanganya baadhi ya dhana kujadiliwa katika Arc Urefu na Curvature na kuongeza kasi vector kupata uelewa zaidi wa jinsi vector hii inahusiana na mwendo katika ndege na katika nafasi. Kumbuka kwamba kitengo tangent vector\(\vecs T\) na kitengo kawaida vector\(\vecs N\) fomu ndege osculating wakati wowote\(P\) juu ya Curve inavyoelezwa na kazi vector-thamani\(\vecs{r}(t)\). Theorem ifuatayo inaonyesha kwamba vector kuongeza kasi\(\vecs{a}(t)\) iko katika ndege osculating na inaweza kuandikwa kama mchanganyiko linear ya kitengo tangent na kitengo vectors kawaida.

Theorem\(\PageIndex{1}\): The Plane of the Acceleration Vector

kuongeza kasi vector\(\vecs{a}(t)\) ya kitu kusonga pamoja Curve kufuatiliwa na kazi mara mbili-differentiable\(\vecs{r}(t)\) liko katika ndege sumu na kitengo tangent vector\(\vecs T(t)\) na kuu kitengo kawaida vector\(\vecs N(t)\) kwa\(C\). Zaidi ya hayo,

\[\vecs{a}(t) = v'(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]

Hapa,\(v(t) = \|\vecs v(t)\|\) ni kasi ya kitu na\(\kappa\) ni curvature ya\(C\) kufuatiliwa nje na\(\vecs{r}(t)\).

Ushahidi

Kwa sababu\(\vecs{v}(t)=\vecs{r}′(t)\) na\(\vecs{T}(t)=\dfrac{\vecs{r}′(t)}{||\vecs{r}′(t)||}\), tuna\(\vecs v(t)=||\vecs{r}′(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).

Sasa tunafafanua usawa huu:

\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \]

Tangu\(\vecs{N}(t)=\dfrac{\vecs{T}′(t)}{||\vecs{T}′(t)||}\), tunajua\(\vecs{T}′(t)=||\vecs{T}′(t)||\vecs{N}(t)\), hivyo

\[\vecs{a}(t)=v′(t)\vecs{T}(t)+v(t)||\vecs{T}′(t)||\vecs{N}(t). \nonumber \]

Fomu ya curvature ni\(\kappa=\dfrac{||\vecs{T}'(t)||}{||\vecs{r}'(t)||}\), hivyo\(\vecs{T}'(t) = \kappa ||\vecs{r}'(t) || = \kappa v(t) \).

Hii inakupa\(\vecs{a}(t)=v′(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)

\(\square\)

Coefficients ya\(\vecs{T}(t)\) na\(\vecs{N}(t)\) hujulikana kama sehemu ya tangential ya kuongeza kasi na sehemu ya kawaida ya kuongeza kasi, kwa mtiririko huo. Tunaandika\(a_\vecs{T}\) ili kuashiria sehemu ya tangential na\(a_\vecs{N}\) kutaja sehemu ya kawaida.

Theorem\(\PageIndex{2}\): Tangential and Normal Components of Acceleration

Hebu\(\vecs{r}(t)\) kuwa kazi yenye thamani ya vector ambayo inaashiria nafasi ya kitu kama kazi ya wakati. Kisha\(\vecs{a}(t)=\vecs{r}′′(t)\) ni vector ya kuongeza kasi. Vipengele vya tangential na vya kawaida vya kuongeza kasi\(a_\vecs{T}\) na\(a_\vecs{N}\) hutolewa na formula

\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]

na

\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]

Vipengele hivi vinahusiana na formula

\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]

Hapa\(\vecs{T}(t)\) ni kitengo tangent vector kwa Curve inavyoelezwa na\(\vecs{r}(t)\), na\(\vecs{N}(t)\) ni kitengo kawaida vector Curve inavyoelezwa na\(\vecs{r}(t)\).

Sehemu ya kawaida ya kuongeza kasi pia inaitwa sehemu ya centripetal ya kuongeza kasi au wakati mwingine sehemu ya radial ya kuongeza kasi. Ili kuelewa kasi ya centripetal, tuseme unasafiri kwenye gari kwenye kufuatilia mviringo kwa kasi ya mara kwa mara. Kisha, kama tulivyoona mapema, vector ya kuongeza kasi inaelekea katikati ya kufuatilia wakati wote. Kama mpanda farasi katika gari, kujisikia kuvuta kuelekea nje ya kufuatilia kwa sababu wewe ni daima kugeuka. Hisia hii hufanya kinyume chake cha kuongeza kasi ya centripetal. Hiyo inashikilia kweli kwa njia zisizo za mviringo. Sababu ni kwamba mwili wako huelekea kusafiri katika mstari wa moja kwa moja na kupinga nguvu kutokana na kuongeza kasi kwamba kushinikiza kuelekea upande. Kumbuka kuwa\(B\) katika hatua katika Kielelezo\(\PageIndex{4}\) vector kuongeza kasi ni akizungumzia nyuma. Hii ni kwa sababu gari ni decelerating kama inakwenda katika Curve.

Kielelezo\(\PageIndex{4}\): Vipengele vya tangential na vya kawaida vya kuongeza kasi vinaweza kutumika kuelezea vector ya kuongeza kasi.

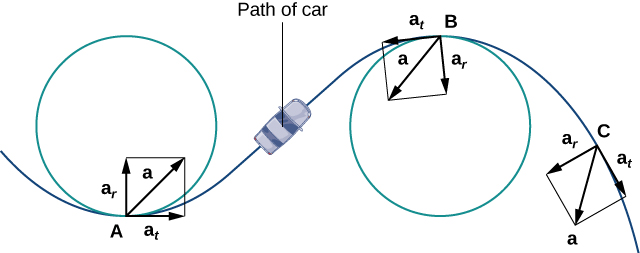
Vectors tangential na ya kawaida kitengo katika hatua yoyote juu ya Curve kutoa sura ya kumbukumbu katika hatua hiyo. Vipengele vya kawaida na vya kawaida vya kuongeza kasi ni makadirio ya vector ya kuongeza kasi kwenye\(\vecs T\) na\(\vecs N\), kwa mtiririko huo.

Mfano\(\PageIndex{2}\): Finding Components of Acceleration

Chembe huenda katika njia inayofafanuliwa na kazi yenye thamani ya vector\(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), ambapo\(t\) hatua wakati katika sekunde na umbali hupimwa kwa miguu.

1. Kupata\(a_\vecs{T}\) na\(a_\vecs{N}\) kama kazi ya\(t\).
2. Pata\(a_\vecs{T}\) na\(a_\vecs{N}\) wakati\(t=2\).

Suluhisho

1. Hebu tuanze kupata kasi na kazi za kuongeza kasi:

   \[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}'(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Sasa tunatumia Equation\ ref {Eq1B}:\[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] Sasa tunaweza kutumia Equation\ ref {Eq2B}:

   \[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]

2. Lazima tathmini kila moja ya majibu kutoka sehemu a katika\(t=2\):

   \[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]

   Vitengo vya kuongeza kasi ni miguu kwa mraba wa pili, kama vile vitengo vya vipengele vya kawaida na vya tangential vya kuongeza kasi.

Zoezi\(\PageIndex{2}\)

kitu hatua katika njia inavyoelezwa na kazi vector-thamani\(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), ambapo\(t\) hatua wakati katika sekunde.

1. Kupata\(a_\vecs{T}\) na\(a_\vecs{N}\) kama kazi ya\(t\).
2. Pata\(a_\vecs{T}\) na\(a_\vecs{N}\) wakati\(t=−3\).

Kidokezo

Tumia equations\ ref {Eq1B} na\ ref {Eq2B}

Jibu

a.\[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r'(t) \cdot \vecs r''(t) }{||\vecs r'(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]

b.\[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]

Projectile Motion

Sasa hebu tuangalie matumizi ya kazi za vector. Hasa, hebu tuchunguze athari za mvuto juu ya mwendo wa kitu wakati unasafiri kupitia hewa, na jinsi inavyoamua trajectory inayosababisha kitu hicho. Katika zifuatazo, tunapuuza athari za upinzani wa hewa. Hali hii, ikiwa na kitu kinachohamia kwa kasi ya awali lakini bila vikosi vinavyofanya hivyo isipokuwa mvuto, hujulikana kama mwendo wa projectile. Inaelezea mwendo wa vitu kutoka mipira ya golf kwa baseballs, na kutoka mishale ya cannonballs.

Kwanza tunahitaji kuchagua mfumo wa kuratibu. Ikiwa tunasimama kwenye asili ya mfumo huu wa kuratibu, basi tunachagua chanya\(y\) -axis kuwa juu, mhimili hasi\(y\) kuwa chini, na mhimili mzuri\(x\) wa kuwa mbele (yaani, mbali na mchezaji wa kitu). Athari ya mvuto iko katika mwelekeo wa kushuka, hivyo sheria ya pili ya Newton inatuambia kwamba nguvu juu ya kitu kinachotokana na mvuto ni sawa na masi ya kitu mara kasi inayotokana na mvuto, au\(\vecs F_g=m\vecs a\), ambapo\(\vecs F_g\) inawakilisha nguvu kutoka mvuto na\(\vecs a = -g\,\hat{\mathbf j}\) inawakilisha kuongeza kasi kutokana na mvuto katika uso wa dunia. Thamani ya mfumo wa\(g\) kipimo cha Kiingereza ni takriban 32 ft/sec ² na ni takriban 9.8 m/sec ² katika mfumo wa metri. Hii ndiyo nguvu pekee inayofanya kitu. Kwa kuwa mvuto vitendo katika mwelekeo chini, tunaweza kuandika nguvu kutokana na mvuto katika fomu\(\vecs F_g=−mg\,\hat{\mathbf j}\), kama inavyoonekana katika Kielelezo\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\): Kitu kinaanguka chini ya ushawishi wa mvuto.

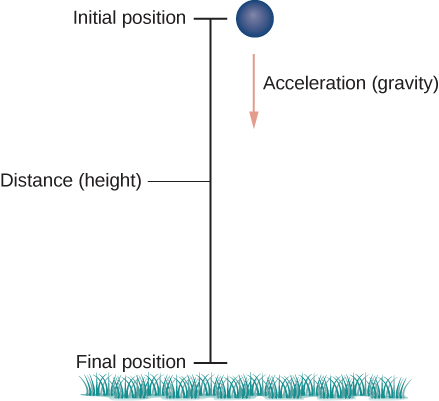
Sheria ya pili ya Newton pia inatuambia kwamba\(F=m\vecs{a}\), ambapo\(\vecs a\) inawakilisha vector kuongeza kasi ya kitu. Nguvu hii lazima iwe sawa na nguvu ya mvuto wakati wote, kwa hiyo tunajua kwamba

\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]

Sasa tunatumia ukweli kwamba vector ya kuongeza kasi ni derivative ya kwanza ya vector kasi. Kwa hiyo, tunaweza kuandika upya equation ya mwisho katika fomu

\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]

Kwa kuchukua antiderivative ya kila upande wa equation hii tunapata

\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]

kwa vector baadhi ya mara kwa mara\(\vecs C_1\). Kuamua thamani ya vector hii, tunaweza kutumia kasi ya kitu kwa wakati uliowekwa, sema wakati\(t=0\). Tunaita kasi hii kasi ya awali:\(\vecs v(0)=\vecs v_0\). Kwa hiyo,\(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) na\(\vecs C_1= \vecs v_0\). Hii inakupa kasi vector kama\(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).

Halafu tunatumia ukweli kwamba kasi\(\vecs{v}(t)\) ni derivative ya nafasi\(\vecs{s}(t)\). Hii inatoa equation

\[\vecs s'(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]

Kuchukua antiderivative ya pande zote mbili za equation hii inaongoza kwa

\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]

na mwingine haijulikani vector mara kwa mara\(\vecs{C}_2\). Kuamua thamani ya\(\vecs{C}_2\), tunaweza kutumia nafasi ya kitu kwa wakati fulani, kusema wakati\(t=0\). Tunaita nafasi hii nafasi ya kwanza:\(\vecs{s}(0)=\vecs{s}_0\). Kwa hiyo,\(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). Hii inatoa nafasi ya kitu wakati wowote kama

\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]

Hebu tuangalie kwa karibu kasi ya awali na nafasi ya awali. Hasa, tuseme kitu kinatupwa juu kutoka kwa asili\(\theta\) kwa pembe kwa usawa, na kasi ya awali\(\vecs{v}_0\). Tunawezaje kurekebisha matokeo ya awali ili kutafakari hali hii? Kwanza, tunaweza kudhani ni kutupwa kutoka asili. Ikiwa sio, basi tunaweza kuhamisha asili hadi mahali ambapo inatupwa. Kwa hiyo\(\vecs{s}_0=\vecs{0}\), kama inavyoonekana katika Kielelezo\(\PageIndex{6}\).

Kielelezo\(\PageIndex{6}\): Projectile mwendo wakati kitu ni kutupwa zaidi kwa angle ρ. Mwendo usio na usawa ni kasi ya mara kwa mara na mwendo wa wima una kasi ya mara kwa mara.

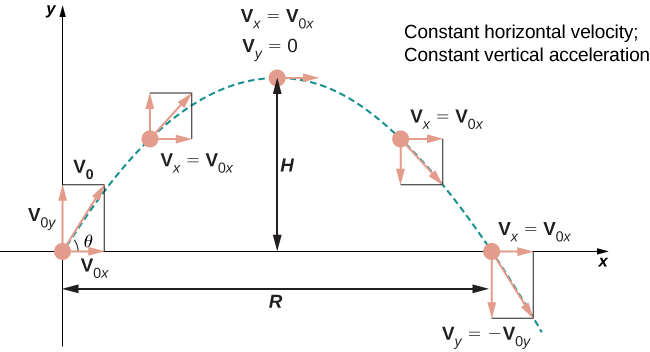
Tunaweza kuandika upya vector ya awali ya kasi katika fomu\(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Kisha equation kwa ajili ya kazi nafasi\(\vecs{s}(t)\) inakuwa

\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]

Mgawo wa\(\hat{\mathbf i}\) inawakilisha sehemu ya usawa\(\vecs{s}(t)\) na ni umbali usio na usawa wa kitu kutoka kwa asili kwa wakati\(t\). Thamani ya juu ya umbali wa usawa (kipimo kwa urefu sawa wa awali na wa mwisho) inaitwa upeo\(R\). Mgawo wa\(\hat{\mathbf j}\) inawakilisha sehemu ya wima ya\(\vecs{s}(t)\) na ni urefu wa kitu kwa wakati\(t\). Thamani ya juu ya umbali wa wima ni urefu\(H\).

Mfano\(\PageIndex{3}\): Motion of a Cannonball

Wakati wa sherehe ya Siku ya Uhuru, cannonball inafukuzwa kutoka kwenye kanuni kwenye mwamba kuelekea maji. Cannon ina lengo la angle ya 30° juu ya usawa na kasi ya awali ya cannonball ni 600 ft/sec. Mwamba ni 100 ft juu ya maji (Kielelezo\(\PageIndex{7}\)).

1. Pata urefu wa juu wa cannonball.
2. Itachukua muda gani kwa cannonball kupasuka ndani ya bahari?
3. Jinsi mbali nje ya bahari cannonball hit maji?

Kielelezo\(\PageIndex{7}\): Ndege ya cannonball (kupuuza upinzani wa hewa) ni mwendo wa projectile.

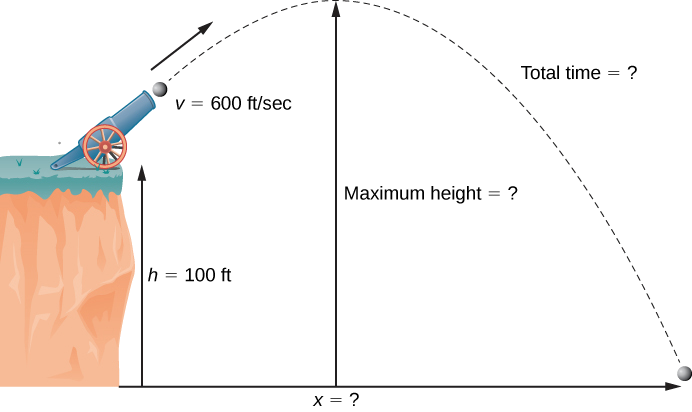
Suluhisho

Tunatumia equation

\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]

kwa\(\theta=30^\circ \),\(g=32 \dfrac{\text{ft}}{\text{sec}^2}\), na\(v_0=600 \dfrac{\text{ft}}{\text{sec}^2}\). Kisha equation nafasi inakuwa

\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]

1. Cannonball hufikia urefu wake wa juu wakati sehemu ya wima ya kasi yake ni sifuri, kwa sababu cannonball haitoi wala kuanguka wakati huo. Vector kasi ni

   \[\begin{align*} \vecs{v}(t) &=\vecs s'(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]

   Kwa hiyo, sehemu ya wima ya kasi hutolewa na maneno\(300−32t\). Kuweka maneno haya sawa na sifuri na kutatua kwa t inatoa\(t=9.375\) sec. Urefu wa cannonball kwa wakati huu hutolewa na sehemu ya wima ya vector ya nafasi, iliyopimwa saa\(t=9.375\).

   \[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]

   Kwa hiyo, urefu wa juu wa cannonball ni 1406.39 ft juu ya kanuni, au 1506.39 ft juu ya usawa wa bahari.
2. Wakati cannonball ardhi katika maji, ni 100 ft chini ya kanuni. Kwa hiyo, sehemu ya wima ya vector nafasi ni sawa na -100. Kuweka sehemu ya wima ya\(\vecs s(t)\) sawa na -100 na kutatua, tunapata

   \[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]

   Thamani nzuri ya\(t\) kwamba hutatua equation hii ni takriban 19.08. Kwa hiyo, cannonball hupiga maji baada ya takriban 19.08 sec.
3. Ili kupata umbali wa baharini, sisi tu badala ya jibu kutoka sehemu (b) katika\(\vecs{s}(t)\):

   \[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]

   Kwa hiyo, mpira hupiga maji kuhusu 9914.26 ft mbali na msingi wa mwamba. Angalia kwamba sehemu ya wima ya vector ya msimamo ni karibu sana na -100, ambayo inatuambia kwamba mpira hupiga maji tu. Kumbuka kuwa 9914.26 miguu si mbalimbali ya kweli ya kanuni tangu nchi Cannonball katika bahari katika eneo chini ya kanuni. Mbalimbali ya kanuni itakuwa kuamua kwa kutafuta jinsi mbali nje cannonball ni wakati urefu wake ni 100 ft juu ya maji (sawa na urefu wa cannon).

Zoezi\(\PageIndex{3}\)

Mpiga upinde anapiga mshale kwenye pembe ya 40° juu ya usawa na kasi ya awali ya 98 m/sec. Urefu wa upinde ni cm 171.5. Find umbali usawa arrow husafiri kabla ya hits ya ardhi.

Kidokezo

Equation kwa vector nafasi inahitaji akaunti kwa urefu wa upinde katika mita.

Jibu

967.15 m

Swali moja la mwisho linabakia: Kwa ujumla, umbali wa juu wa projectile unaweza kusafiri, kutokana na kasi yake ya awali? Kuamua umbali huu, tunadhani projectile inafukuzwa kutoka ngazi ya chini na tunataka kurudi ngazi ya chini. Kwa maneno mengine, tunataka kuamua equation kwa aina mbalimbali. Katika kesi hiyo, equation ya mwendo projectile ni

\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]

Kuweka sehemu ya pili sawa na sifuri na kutatua kwa\(t\) mavuno

\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]

Kwa hiyo, ama\(t=0\) au\(t=\dfrac{2v_0\sin\theta}{g}\). Sisi ni nia ya thamani ya pili ya\(t\), hivyo sisi badala hii katika\(\vecs{s}(t)\), ambayo inatoa

\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]

Hivyo, kujieleza kwa aina mbalimbali ya projectile fired kwa pembeni\(\theta\) ni

\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]

Variable tu katika maneno haya ni\( \theta\). Ili kuongeza umbali uliosafiri, chukua derivative ya mgawo wa i kwa heshima\(\theta\) na kuiweka sawa na sifuri:

\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]

Thamani hii ya\(\theta)\) ni ndogo chanya thamani ambayo inafanya derivative sawa na sifuri. Kwa hiyo, kwa kutokuwepo kwa upinzani wa hewa, angle bora ya moto projectile (ili kuongeza upeo) iko kwenye angle ya 45°. Umbali unaotembea unatolewa na

\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]

Kwa hiyo, upeo wa angle ya 45° ni\(\frac{v_0^2}{g}\) vitengo.

Sheria za Kepler

Wakati wa miaka ya 1600 mapema, Johannes Kepler aliweza kutumia data sahihi ya kushangaza kutoka kwa mshauri wake Tycho Brahe kuunda sheria zake tatu za mwendo wa sayari, ambazo sasa zinajulikana kama sheria za Kepler za mwendo wa sayari. Sheria hizi zinatumika pia kwa vitu vingine katika mfumo wa jua katika obiti kuzunguka Jua, kama vile comets (k.m. comet Halley) na asteroidi. Tofauti ya sheria hizi zinatumika kwa satelaiti katika obiti kote duniani.

Theorem\(\PageIndex{2}\): Kepler's Laws of Planetary Motion

1. Njia ya sayari yoyote kuhusu Jua ni sura ya elliptical, na katikati ya Jua iko kwenye lengo moja la duaradufu (sheria ya ellipses).
2. Mstari unaotokana na katikati ya Jua hadi katikati ya sayari hutoa maeneo sawa kwa vipindi sawa (sheria ya maeneo sawa) (Kielelezo\(\PageIndex{8}\)).
3. Uwiano wa mraba wa vipindi vya sayari yoyote mbili ni sawa na uwiano wa cubes ya urefu wa axes zao za semimajor orbital (Sheria ya Harmonies).

Kielelezo\(\PageIndex{8}\): Sheria ya kwanza na ya pili ya Kepler ni picha hapa. Jua liko kwenye lengo la obiti ya elliptical ya sayari yoyote. Zaidi ya hayo, maeneo yenye kivuli ni sawa, kudhani kwamba kiasi cha muda kinachopimwa kama sayari inakwenda ni sawa kwa kila mkoa.

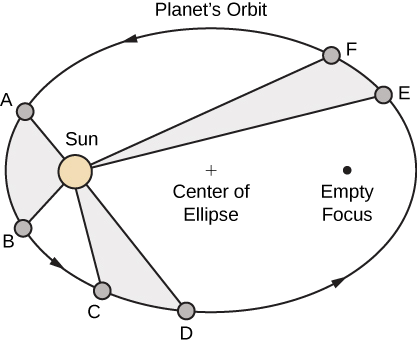
Sheria ya tatu ya Kepler ni muhimu hasa wakati wa kutumia vitengo vinavyofaa. Hasa kitengo cha astronomia 1 kinafafanuliwa kuwa umbali wa wastani kutoka Dunia hadi Jua, na sasa kinatambuliwa kuwa m 149,597,870,700 au, takriban mi 93,000,000. Kwa hiyo tunaandika 1 A.U. = 93,000,000 mi. Tangu muda unaotumika kwa Dunia kuizunguka Jua ni mwaka 1, tunatumia miaka ya Dunia kwa vitengo vya wakati. Kisha, kubadilisha mwaka 1 kwa kipindi cha Dunia na 1 A.U. kwa umbali wa wastani wa Jua, sheria ya tatu ya Kepler inaweza kuandikwa kama

\[ T_p^2=D_p^3 \nonumber \]

kwa sayari yoyote katika mfumo wa jua, ambapo\(T_P\) ni kipindi cha sayari hiyo kinachopimwa katika miaka ya dunia na\(D_P\) ni umbali wa wastani kutoka sayari hiyo hadi Jua unaopimwa kwa vitengo vya astronomia. Kwa hiyo, ikiwa tunajua umbali wa wastani kutoka sayari hadi Jua (katika vitengo vya astronomical), tunaweza kuhesabu urefu wa mwaka wake (katika miaka ya Dunia), na kinyume chake.

Sheria za Kepler ziliandaliwa kulingana na uchunguzi kutoka kwa Brahe; hata hivyo, hazikuthibitishwa rasmi mpaka Sir Isaac Newton alipoweza kutumia hesabu. Zaidi ya hayo, Newton aliweza kuzalisha sheria ya tatu ya Kepler kwa mifumo mingine ya orbital, kama vile mwezi unaozunguka sayari. Sheria ya tatu ya awali ya Kepler inatumika tu kwa vitu vinavyozunguka Jua.

Ushahidi

Hebu sasa tuhakikishe sheria ya kwanza ya Kepler kwa kutumia hesabu ya kazi za thamani ya vector. Kwanza tunahitaji mfumo wa kuratibu. Hebu tuweke jua kwa asili ya mfumo wa kuratibu na basi kazi yenye thamani ya vector\(\vecs{r}(t)\) inawakilisha eneo la sayari kama kazi ya wakati. Newton alithibitisha sheria ya Kepler akitumia sheria yake ya pili ya mwendo na sheria yake ya gravitation zima. Sheria ya pili ya Newton ya mwendo inaweza kuandikwa kama\(\vecs{F}=m\vecs{a}\), ambapo\(\vecs{F}\) inawakilisha nguvu wavu kaimu katika dunia. Sheria yake ya uvunjaji wa ulimwengu wote inaweza kuandikwa kwa fomu\(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), ambayo inaonyesha kwamba nguvu inayotokana na mvuto wa mvuto wa Jua inarudi kuelekea jua, na ina ukubwa\(\dfrac{GmM}{||\vecs{r}||^2} \) (Kielelezo\(\PageIndex{9}\)).

Kielelezo\(\PageIndex{9}\): Nguvu ya mvuto kati ya Dunia na Jua ni sawa na wingi wa dunia mara kuongeza kasi yake.

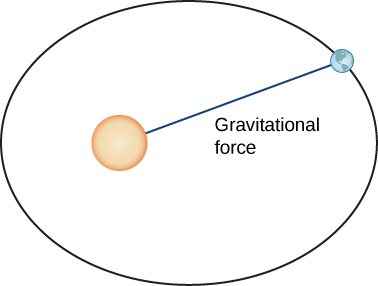
Kuweka vikosi hivi viwili sawa na kila mmoja, na kwa kutumia ukweli kwamba\(\vecs a(t)=\vecs v′(t)\), tunapata

\[ m\vecs v′(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]

ambayo inaweza kuandikwa upya kama

\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]

Equation hii inaonyesha kwamba wadudu\(d\vecs{v}/dt\) na\(\vecs r\) ni sambamba na kila mmoja, hivyo\(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). Kisha, hebu tufanye tofauti\(\vecs{r} \times \vecs{v}\) kwa heshima na wakati:

\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]

Hii inathibitisha kwamba\(\vecs{r}\times\vecs{v}\) ni vector mara kwa mara, ambayo tunaita\(\vecs C\). Tangu\(\vecs r\) na wote\(\vecs v\) ni perpendicular\(\vecs C\) kwa maadili yote ya\(t\), lazima uongo katika ndege perpendicular kwa\(\vecs C\). Kwa hiyo, mwendo wa sayari upo katika ndege.

Halafu tunahesabu maneno\(d\vecs{v}/dt\times \vecs C\):

\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]

Usawa wa mwisho katika Equation\ ref {Eq10} unatoka kwa formula ya bidhaa ya msalaba mara tatu (Utangulizi wa Vectors katika Nafasi). Tunahitaji kujieleza kwa\(\vecs{r}\cdot \vecs{v}\). Ili kuhesabu hili, tunafautisha\(\vecs{r}\cdot \vecs{r}\) kwa heshima na wakati:

\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]

Tangu\(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), sisi pia

\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]

Kuchanganya Equation\ ref {Eq12} na Equation\ ref {Eq13}, tunapata

\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]

Kubadilisha hii katika Equation\ ref {Eq11} inatupa

\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]

Hata hivyo,

\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]

Kwa hiyo, Equation\ ref {Eq15} inakuwa

\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]

Kwa kuwa\(\vecs{C}\) ni vector mara kwa mara, tunaweza kuunganisha pande zote mbili na kupata

\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]

ambapo\(\vecs D\) ni vector mara kwa mara. Lengo letu ni kutatua\(|| \vecs{r} ||\). Hebu tuanze kwa kuhesabu\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\):

\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]

Hata hivyo\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), hivyo

\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]

Tangu\(\vecs{r}\times \vecs{v}=\vecs{C}\), tuna

\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]

Kumbuka kwamba\( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \),\(\theta\) wapi pembe kati\(\vecs{r}\) na\(\vecs{D}\). Kwa hiyo,

\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]

Kutatua kwa\(||\vecs{r}||\),

\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]

wapi\(e=||\vecs{D}||/GM\). Hii ni equation polar ya conic na lengo katika asili, ambayo sisi kuanzisha kuwa Sun. Ni hyperbola kama\(e>1\), parabola kama\(e=1\), au duaradufu kama\(e<1\). Kwa kuwa sayari zimefungwa njia, uwezekano pekee ni duaradufu. Hata hivyo, katika hatua hii inapaswa kutajwa kuwa comets hyperbolic zipo. Hizi ni vitu ambavyo vinapita tu katika mfumo wa jua kwa kasi kubwa mno ili kuingizwa katika obiti kuzunguka Jua. Wakati wanapopita karibu na Jua, uwanja wa mvuto wa Jua hupunguza trajectory ya kutosha hivyo njia inakuwa hyperbolic.

\(\square\)

Sheria ya tatu ya Kepler ya mwendo wa sayari inaweza kubadilishwa kuwa kesi ya kitu kimoja katika obiti kuzunguka kitu kingine isipokuwa Jua, kama vile Mwezi unaozunguka Dunia. Katika kesi hiyo, sheria ya tatu ya Kepler inakuwa

\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]

ambapo m ni masi ya Mwezi na M ni masi ya Dunia, a inawakilisha urefu wa mhimili mkuu wa obiti ya elliptical, na P inawakilisha kipindi.

Mfano\(\PageIndex{4}\): Using Kepler’s Third Law for Nonheliocentric Orbits

Kutokana na kwamba wingi wa Mwezi ni\(7.35\times 10^{22}\) kilo, masi ya Dunia ni\(5.97\times 10^{24}\) kilo,\(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\), na kipindi cha mwezi ni siku 27.3, hebu tupate urefu wa mhimili mkubwa wa obiti ya Mwezi karibu na Dunia.

Suluhisho

Ni muhimu kuwa sawa na vitengo. Kwa kuwa mara kwa mara ya mvuto wote ina sekunde katika vitengo, tunahitaji kutumia sekunde kwa kipindi cha Mwezi pia:

\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]

Badilisha data zote katika Equation\ ref {Eq30} na kutatua kwa\(a\):

\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]

Uchambuzi

Kulingana na solarsystem.nasa.gov, umbali halisi wa wastani kutoka Mwezi hadi Dunia ni kilomita 384,400. Hii ni mahesabu kwa kutumia reflectors kushoto juu ya Mwezi na Apollo wanaanga nyuma katika miaka ya 1960.

Zoezi\(\PageIndex{4}\)

Titan ni mwezi mkubwa wa Saturn. Uzito wa Titan ni takriban\(1.35 \times 10^{23} kg\). Uzito wa Saturn ni takriban\( 5.68 \times 10^{26}\) kilo. Titan inachukua takriban siku 16 kwa obiti Saturn. Tumia habari hii, pamoja na mara kwa mara ya gravitation ya jumla\(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) ili kukadiria umbali kutoka Titan hadi Saturn.

Kidokezo

Hakikisha vitengo vyako vinakubaliana, kisha utumie Equation\ ref {Eq30}.

Jibu

\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]

Mfano\(\PageIndex{5}\): Halley’s Comet

Sasa tunarudi kwenye kopo ya sura, ambayo inazungumzia mwendo wa kimondo cha Halley karibu na Jua. Sheria ya kwanza ya Kepler inasema kuwa kimondo cha Halley kinafuata njia ya duaradufu inayozunguka Jua, huku Jua kama lengo moja la duaradufu. Kipindi cha kimondo cha Halley ni takriban miaka 76.1, kulingana na jinsi unavyopita karibu na Jupiter na Saturn inapita kupitia mfumo wa jua wa nje. Hebu tumia\(T=76.1\) miaka. Umbali wa wastani wa comet Halley kutoka Jua ni nini?

Suluhisho

Kutumia equation\(T^2=D^3\) na\(T=76.1\), sisi kupata\(D^3=5791.21\), hivyo\(D\approx 17.96\) A.U Hii inakuja nje ya takriban\(1.67\times 10^9\) mi.

Swali la asili la kuuliza ni: Je, ni kiwango cha juu (aphelion) na kiwango cha chini (perihelion) umbali kutoka Comet Halley hadi Jua? Uwezo wa obiti ya Comet ya Halley ni 0.967 (Chanzo: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Kumbuka kwamba formula ya eccentricity ya duaradufu ni\(e=c/a\), ambapo ni urefu wa mhimili wa semimajor na c ni umbali kutoka katikati hadi kuzingatia. Kwa hiyo,\(0.967=c/17.96\) na\(c\approx 17.37\) A.U. kutoa hii kutoka anatoa perihelion umbali\(p=a−c=17.96−17.37=0.59\) A.U. kulingana na Kituo cha Taifa cha Sayansi ya Nafasi (chanzo: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), umbali perihelion kwa Comet Halley ni 0.587 A.U Ili kuhesabu umbali wa aphelion, tunaongeza

\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]

Hii ni takriban\(3.3\times 10^9\) mi. Umbali wa wastani kutoka Pluto hadi Jua ni 39.5 A.U. (Chanzo: http://www.oarval.org/furthest.htm), hivyo ingeonekana kwamba Comet ya Halley inakaa tu ndani ya obiti ya Pluto.

PUNDE KUGEUKA BENKI

Je! Haraka ya racecar inaweza kusafiri kwa njia ya kugeuka kwa mviringo bila skidding na kupiga ukuta? Jibu linaweza kutegemea mambo kadhaa:

• Uzito wa gari;
• Msuguano kati ya matairi na barabara;
• Radi ya mduara;
• “Mwinuko” wa upande.

Katika mradi huu sisi kuchunguza swali hili kwa NASCAR racecars katika Bristol Motor Speedway katika Tennessee. Kabla ya kuzingatia wimbo huu hasa, tunatumia kazi za vector kuendeleza hisabati na fizikia muhimu kwa kujibu maswali kama haya.

Gari la molekuli\(m\) huenda kwa kasi ya angular mara kwa mara\(\omega\) karibu na pembe ya mviringo ya radius\(R\) (Kielelezo\(\PageIndex{9}\)). Curve ni banked kwa pembe\(\theta\). Ikiwa urefu wa gari mbali ya ardhi ni\(h\), basi nafasi ya gari wakati\(t\) hutolewa na kazi\(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

Kielelezo\(\PageIndex{9}\): Maoni ya gari la mbio linalozunguka kufuatilia.

1. Pata kazi\(\vecs{v}(t)\) ya kasi ya gari. Onyesha kwamba\(\vecs{v}\) ni tangent kwa Curve mviringo. Hii inamaanisha kwamba, bila nguvu ya kuweka gari kwenye pembe, gari litaondoa.
2. Onyesha kwamba kasi ya gari ni\(\omega R\). Tumia hii ili kuonyesha kwamba\((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
3. Kupata kuongeza kasi\(\vecs{a}\). Onyesha kwamba vector hii inaonyesha kuelekea katikati ya mduara na kwamba\(\|\vecs{a}\|=R\omega ^2\).
4. Nguvu inayotakiwa kuzalisha mwendo huu wa mviringo inaitwa nguvu ya centripetal, na inaashiria\( \vecs{F}_{cent} \). Nguvu hii inaelezea kuelekea katikati ya mduara (sio chini). Onyesha hilo\(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\).

Kama gari inakwenda karibu na pembe, majeshi matatu hufanya juu yake: mvuto, nguvu inayotumiwa na barabara (nguvu hii ni perpendicular kwa ardhi), na nguvu ya msuguano (Kielelezo\(\PageIndex{10}\)). Kwa sababu kuelezea nguvu msuguano yanayotokana na matairi na barabara ni ngumu, tunatumia makadirio ya kiwango kwa nguvu msuguano. Kudhani kwamba\(\vecs{f}=\mu \vecs{N}\) kwa baadhi ya mara kwa mara chanya\(\mu \). Mara kwa mara\(\mu\) huitwa mgawo wa msuguano.

Kielelezo\(\PageIndex{10}\): Gari ina vikosi vitatu vinavyofanya juu yake: mvuto (uliotajwa na\(m\vecs g\))\(\vecs f\), nguvu ya msuguano, na nguvu inayotumiwa na barabara\(\vecs N\).

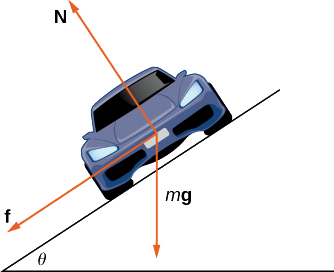
Hebu\(v_{max}\) kuashiria kasi ya juu ya gari inaweza kufikia kupitia Curve bila skidding. Kwa maneno mengine,\(v_{max}\) ni kasi ya kasi ambayo gari inaweza navigate upande. Wakati gari linasafiri kwa kasi hii, ukubwa wa nguvu ya centripetal ni

\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]

Maswali matatu yafuatayo yanashughulikia kuendeleza formula inayohusiana na kasi\(v_{max}\) kwa angle ya benki\(\theta\).

5. Onyesha hilo\(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Kuhitimisha kwamba\(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
6. Nguvu ya centripetal ni jumla ya majeshi katika mwelekeo usio na usawa, kwani nguvu ya centripetal inaelezea kuelekea katikati ya mviringo wa mviringo. Onyesha kwamba

   \[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]

   Kuhitimisha kwamba

   \[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]

7. Onyesha hilo\((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\). Kuhitimisha kuwa kasi ya juu haina kweli hutegemea wingi wa gari.
   Sasa kwa kuwa tuna formula inayohusiana na kasi ya juu ya gari na angle ya benki, tuko katika nafasi ya kujibu maswali kama yale yaliyotokana mwanzoni mwa mradi huo.
   Bristol Motor Speedway ni wimbo mfupi wa NASCAR huko Bristol, Tennessee. kufuatilia ina sura takriban inavyoonekana katika Kielelezo\(\PageIndex{11}\). Kila mwisho wa wimbo ni takriban semicircular, hivyo wakati magari kufanya zamu wao ni kusafiri pamoja Curve takriban mviringo. Ikiwa gari litachukua wimbo wa ndani na kasi chini ya zamu ya 1, gari linasafiri kwenye nusu-duara ya radius takriban futi 211 ikiwa na angle ya benki ya 24°. Ikiwa gari linapoamua kuchukua wimbo wa nje na kasi juu ya upande wa 1, basi gari linasafiri kando ya semicircle yenye angle ya benki ya 28°. (Wimbo ina variable angle benki.)

Kielelezo\(\PageIndex{11}\): Katika Bristol Motor Speedway, Bristol, Tennessee (a), zamu zina radius ya ndani ya futi 211 na upana wa futi 40 (b). (mikopo: sehemu (a) picha na Raniel Diaz, Flickr)

Mgawo wa msuguano kwa tairi ya kawaida katika hali kavu ni takriban 0.7. Kwa hiyo, tunadhani mgawo wa tairi ya NASCAR katika hali kavu ni takriban 0.98.

Kabla ya kujibu maswali yafuatayo, kumbuka kuwa ni rahisi kufanya hesabu kwa suala la miguu na sekunde, na kisha kubadilisha majibu kwa maili kwa saa kama hatua ya mwisho.

8. Katika hali kavu, gari linaweza kusafiri kwa kasi kwa njia ya chini ya upande bila skidding?
9. Katika hali kavu, gari linaweza kusafiri kwa kasi kwa njia ya juu ya upande bila skidding?
10. Katika hali ya mvua, mgawo wa msuguano unaweza kuwa chini kama 0.1. Ikiwa ndio kesi, gari linaweza kusafiri kwa kasi kwa njia ya chini ya upande bila skidding?
11. Tuseme kasi ya kipimo cha gari kinachoenda kando ya nje ya upande ni 105 mph. Tathmini mgawo wa msuguano kwa matairi ya gari.

Dhana muhimu

• Ikiwa\(\vecs{r}(t)\) inawakilisha nafasi ya kitu kwa wakati t, basi\(\vecs{r}'(t)\) inawakilisha kasi na\(\vecs{r}′′(t)\) inawakilisha kuongeza kasi ya kitu kwa wakati t. ukubwa wa vector kasi ni kasi.
• vector kuongeza kasi daima anasema upande concave ya Curve inavyoelezwa na\(\vecs{r}(t)\). Vipengele vya kawaida na vya kawaida vya kuongeza kasi\(a_\vecs{T}\) na\(a_\vecs{N}\) ni makadirio ya vector ya kuongeza kasi kwenye kitengo cha tangent na kitengo cha vectors kawaida kwa pembe.
• Sheria tatu za Kepler za mwendo wa sayari zinaelezea mwendo wa vitu katika obiti kuzunguka Jua. Sheria yake ya tatu inaweza kubadilishwa kuelezea mwendo wa vitu katika obiti kuzunguka vitu vingine vya mbinguni pia.
• Newton aliweza kutumia sheria yake ya gravitation zima kwa kushirikiana na sheria yake ya pili ya mwendo na hesabu ili kuthibitisha sheria tatu za Kepler.

Mlinganyo muhimu

• Velocity\[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
• Kuharakisha\[\vecs{a}(t)=\vecs{v}′(t)=\vecs{r}′′(t) \nonumber \]
• Kasi\[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
• Sehemu ya tangential ya kuongeza kasi\[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
• Sehemu ya kawaida ya kuongeza kasi\[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]

faharasa

kuongeza kasi vector

derivative ya pili ya vector nafasi

Sheria za Kepler za mwendo wa sayari

sheria tatu zinazosimamia mwendo wa sayari, asteroids, na comets katika obiti kuzunguka Sun

sehemu ya kawaida ya kuongeza kasi

mgawo wa kitengo vector kawaida\(\vecs N\) wakati vector kuongeza kasi imeandikwa kama mchanganyiko linear ya\(\vecs T\) na\(\vecs N\)

mwendo wa kusokotoa

mwendo wa kitu kilicho na kasi ya awali lakini hakuna nguvu inayofanya juu yake isipokuwa mvuto

sehemu ya tangential ya kuongeza kasi

mgawo wa kitengo cha vector tangent\(\vecs T\) wakati vector ya kuongeza kasi imeandikwa kama mchanganyiko wa mstari wa\(\vecs T\) na\(\vecs N\)

vector kasi

derivative ya vector nafasi

Wachangiaji na Majina

• Template:ContribOpenStaxCalc
• Edited by Paul Seeburger
  Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
  He also created Figure \(\PageIndex{1}\).