9.2: Mfululizo usio

Malengo ya kujifunza

• Eleza maana ya jumla ya mfululizo usio.
• Tumia jumla ya mfululizo wa kijiometri.
• Tathmini mfululizo wa darubini.

Tumeona kwamba mlolongo ni seti ya amri ya masharti. Ikiwa unaongeza maneno haya pamoja, unapata mfululizo. Katika sehemu hii sisi kufafanua mfululizo usio na kuonyesha jinsi mfululizo ni kuhusiana na Utaratibu. Pia tunafafanua maana gani kwa mfululizo wa kuungana au kuachana. Tunaanzisha moja ya aina muhimu zaidi za mfululizo: mfululizo wa kijiometri. Tutatumia mfululizo wa kijiometri katika sura inayofuata kuandika kazi fulani kama polynomials na idadi isiyo na kipimo cha maneno. Utaratibu huu ni muhimu kwa sababu unatuwezesha kutathmini, kutofautisha, na kuunganisha kazi ngumu kwa kutumia polynomials ambazo ni rahisi kushughulikia. Sisi pia kujadili mfululizo harmonic, arguably kuvutia zaidi tofauti mfululizo kwa sababu tu inashindwa kuungana.

Mfululizo na Mfululizo

Mfululizo usio na kipimo ni jumla ya maneno mengi sana na imeandikwa kwa fomu

\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯.\)

Lakini hii ina maana gani? Hatuwezi kuongeza idadi isiyo na kipimo ya maneno kwa njia ile ile tunaweza kuongeza idadi ya mwisho ya maneno. Badala yake, thamani ya mfululizo usio na kipimo hufafanuliwa kwa suala la kikomo cha kiasi cha sehemu. Jumla ya sehemu ya mfululizo usio na mwisho ni jumla ya fomu

\(\displaystyle \sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k.\)

Ili kuona jinsi tunavyotumia kiasi cha sehemu ili kutathmini mfululizo usio, fikiria mfano unaofuata. Tuseme mafuta yanaingia ndani ya ziwa kiasi kwamba\( 1000\) galoni huingia ziwa wiki ya kwanza. Wakati wa wiki ya pili,\( 500\) galoni za ziada za mafuta huingia ziwa. Wiki ya tatu, galoni\( 250\) zaidi huingia ziwa. Kudhani muundo huu unaendelea kama kwamba kila wiki nusu mafuta mengi huingia ziwa kama walivyofanya wiki iliyopita. Ikiwa hii inaendelea milele, tunaweza kusema nini kuhusu kiasi cha mafuta katika ziwa? Je! Kiasi cha mafuta kinaendelea kupata kiholela kikubwa, au inawezekana kwamba inakaribia kiasi cha mwisho? Ili kujibu swali hili, tunaangalia kiasi cha mafuta katika ziwa baada ya\( k\) wiki. Kuruhusu\( S_k\) kutaja kiasi cha mafuta katika ziwa (kipimo katika maelfu ya galoni) baada ya\( k\) wiki, tunaona kwamba

\( S_1=1\)

\( S_2=1+0.5=1+\frac{1}{2}\)

\( S_3=1+0.5+0.25=1+\frac{1}{2}+\frac{1}{4}\)

\( S_4=1+0.5+0.25+0.125=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\)

\( S_5=1+0.5+0.25+0.125+0.0625=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}.\)

Kuangalia mfano huu, tunaona kwamba kiasi cha mafuta katika ziwa (katika maelfu ya galoni) baada ya\( k\) wiki ni

\[ S_k=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯+\frac{1}{2^{k−1}}=\sum_{n=1}^k\left(\frac{1}{2}\right)^{n−1}. \nonumber \]

Sisi ni nia ya nini kinatokea kama\( k→∞.\) Symbolically, kiasi cha mafuta katika ziwa kama\( k→∞\) ni iliyotolewa na mfululizo usio

\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯. \nonumber \]

Wakati huo huo, kama\( k→∞\), kiasi cha mafuta katika ziwa kinaweza kuhesabiwa kwa kutathmini\(\displaystyle \lim_{k→∞}S_k\). Kwa hiyo, tabia ya mfululizo usio na kipimo inaweza kuamua kwa kuangalia tabia ya mlolongo wa kiasi cha sehemu\( {S_k}\). Ikiwa mlolongo wa kiasi cha sehemu\( {S_k}\) hujiunga, tunasema kwamba mfululizo usio na mwisho hujiunga, na jumla yake hutolewa na\(\displaystyle \lim_{k→∞}S_k\). Ikiwa mlolongo\( {S_k}\) unapungua, tunasema mfululizo usio na kipimo hupungua. Sasa tunageuka mawazo yetu kwa kuamua kikomo cha mlolongo huu\( {S_k}\).

Kwanza, kurahisisha baadhi ya kiasi hiki sehemu, tunaona kwamba

\( S_1=1\)

\( S_2=1+\frac{1}{2}=\frac{3}{2}\)

\( S_3=1+\frac{1}{2}+\frac{1}{4}=\frac{7}{4}\)

\( S_4=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{15}{8}\)

\( S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.\)

Kupanga baadhi ya maadili haya katika Kielelezo, inaonekana kwamba mlolongo\( {S_k}\) inaweza kuwa inakaribia 2.

Kielelezo\(\PageIndex{1}\): Grafu inaonyesha mlolongo wa kiasi cha sehemu\({S_k}\). Inaonekana kwamba mlolongo unakaribia thamani\(2\).

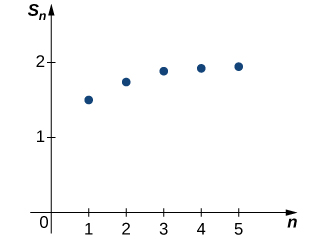
Hebu tuangalie ushahidi zaidi wa kushawishi. Katika meza ifuatayo, sisi orodha maadili ya\(S_k\) kwa maadili kadhaa ya\(k\).

\( k\)	5	10	15	20
\( S_k\)	1.9375	1.998	1.999939	1.999998

Hizi data ugavi ushahidi zaidi na kupendekeza kwamba mlolongo\({S_k}\) hujiunga na\(2\). Baadaye tutatoa hoja ya uchambuzi ambayo inaweza kutumika kuthibitisha hilo\(\displaystyle \lim_{k→∞}S_k=2\). Kwa sasa, tunategemea data ya namba na graphical ili kuwashawishi wenyewe kwamba mlolongo wa kiasi cha sehemu gani kweli hujiunga na\(2\). Kwa kuwa mlolongo huu wa kiasi sehemu hujiunga na\(2\), tunasema mfululizo usio hujiunga\(2\) na kuandika

\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber \]

Kurudi kwenye swali kuhusu mafuta katika ziwa, kwa kuwa mfululizo huu usio na mwisho unajiunga\(2\), tunahitimisha kuwa kiasi cha mafuta katika ziwa kitapata kiholela karibu na\(2000\) galoni kama kiasi cha muda kinapata kutosha.

Mfululizo huu ni mfano wa mfululizo wa kijiometri. Tunajadili mfululizo wa kijiometri kwa undani zaidi baadaye katika sehemu hii. Kwanza, sisi muhtasari maana yake kwa mfululizo usio na mwisho wa kuungana.

Ufafanuzi

Mfululizo usio na mwisho ni usemi wa fomu

\[\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber \]

Kwa kila integer chanya\(k\), jumla

\[S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber \]

inaitwa jumla ya\(k^{\text{th}}\) sehemu ya mfululizo usio. Kiasi cha sehemu huunda mlolongo\({S_k}\). Ikiwa mlolongo wa kiasi cha sehemu hujiunga na idadi halisi\(S\), mfululizo usio na mwisho hujiunga. Kama tunaweza kuelezea muunganiko wa mfululizo kwa\(S\), tunaita jumla\(S\) ya mfululizo, na tunaandika

\[\sum_{n=1}^∞a_n=S. \nonumber \]

Ikiwa mlolongo wa kiasi cha sehemu hupungua, tuna tofauti ya mfululizo.

Kumbuka kuwa index kwa mfululizo haja ya kuanza na\(n=1\) lakini inaweza kuanza na thamani yoyote. Kwa mfano, mfululizo

\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber \]

pia inaweza kuandikwa kama

\[\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber \]

Mara nyingi ni rahisi kwa index kuanza saa\(1\), hivyo kama kwa sababu fulani huanza kwa thamani tofauti, tunaweza re-index kwa kufanya mabadiliko ya vigezo. Kwa mfano, fikiria mfululizo

\[ \sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Kwa kuanzisha variable\(m=n−1\), ili\(n=m+1,\) tuweze kuandika upya mfululizo kama

\[ \sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber \]

Mfano\(\PageIndex{1}\): Evaluating Limits of Sequences of Partial Sums

Kwa kila moja ya mfululizo wafuatayo, tumia mlolongo wa kiasi cha sehemu ili ueleze kama mfululizo unajiunga au hupungua.

1. \(\displaystyle \sum_{n=1}^∞\frac{n}{n+1}\)
2. \(\displaystyle \sum_{n=1}^∞(−1)^n\)
3. \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}\)

Suluhisho

a. mlolongo wa kiasi sehemu\({S_k}\) satisfies

\(S_1=\dfrac{1}{2}\)

\(S_2=\dfrac{1}{2}+\dfrac{2}{3}\)

\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}\)

\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}\).

Kumbuka kwamba kila neno aliongeza ni kubwa kuliko\(1/2\). Matokeo yake, tunaona kwamba

\(S_1=\dfrac{1}{2}\)

\(S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)\)

\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)\)

\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).\)

Kutokana na muundo huu tunaweza kuona kwamba\(S_k>k\left(\frac{1}{2}\right)\) kwa kila integer\(k\). Kwa hiyo,\({S_k}\) ni unbounded na hivyo, diverges. Kwa hiyo, mfululizo usio na kipimo\(\displaystyle \sum^∞_{n=1}\frac{n}{n+1}\) hutofautiana.

b. mlolongo wa kiasi sehemu\({S_k}\) satisfies

\(S_1=−1\)

\(S_2=−1+1=0\)

\(S_3=−1+1−1=−1\)

\(S_4=−1+1−1+1=0.\)

Kutokana na muundo huu tunaweza kuona mlolongo wa kiasi cha sehemu ni

\[{S_k}={−1,0,−1,0,…}. \nonumber \]

Kwa kuwa mlolongo huu unatofautiana, mfululizo usio na kipimo\(\displaystyle \sum^∞_{n=1}(−1)^n\) hupungua.

c. mlolongo wa kiasi sehemu\( {S_k}\) satisfies

\( S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}\)

\( S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\)

\( S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}\)

\( S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}\)

\( S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.\)

Kutoka kwa mfano huu, tunaweza kuona kwamba jumla ya\( k^{\text{th}}\) sehemu hutolewa na formula wazi

\[ S_k=\frac{k}{k+1} \nonumber \].

Kwa kuwa\( k/(k+1)→1,\) tunahitimisha kwamba mlolongo wa kiasi cha sehemu hujiunga, na kwa hiyo mfululizo usio hujiunga na\( 1\). Tuna

\[ \sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber \]

Zoezi\(\PageIndex{1}\)

Kuamua kama mfululizo\(\displaystyle \sum^∞_{n=1}\frac{n+1}{n}\) hujiunga au hupungua.

Kidokezo

Angalia mlolongo wa kiasi cha sehemu.

Jibu

Mfululizo hutofautiana kwa sababu jumla ya\( k^{\text{th}}\) sehemu\( S_k>k\).

mfululizo harmonic

Mfululizo muhimu kujua kuhusu ni mfululizo wa harmonic. Mfululizo wa harmonic hufafanuliwa kama

\[\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber \]

Mfululizo huu ni wa kuvutia kwa sababu unatofautiana, lakini hupungua polepole sana. Kwa hili tuna maana kwamba maneno katika mlolongo wa kiasi sehemu\( {S_k}\) mbinu infinity, lakini kufanya hivyo polepole sana. Tutaonyesha kwamba mfululizo hupungua, lakini kwanza tunaonyesha ukuaji wa polepole wa maneno katika mlolongo\( {S_k}\) katika meza ifuatayo.

\( k\)	10	100	1000	10,00	100,000	1,000,000
\( S_k\)	2.92897	5.18738	7.48547	9.78761	12.09015	14.39273

Hata baada ya\( 1,000,000\) maneno, jumla ya sehemu bado ni ndogo. Kutoka meza hii, haijulikani kuwa mfululizo huu hupungua. Hata hivyo, tunaweza kuonyesha kwa uchambuzi kwamba mlolongo wa kiasi cha sehemu hupungua, na kwa hiyo mfululizo hupungua.

Ili kuonyesha kwamba mlolongo wa kiasi cha sehemu hutofautiana, tunaonyesha kwamba mlolongo wa kiasi cha sehemu ni unbounded. Tunaanza kwa kuandika kiasi cha kwanza cha sehemu kadhaa:

\( S_1=1\)

\( S_2=1+\dfrac{1}{2}\)

\( S_3=1+\dfrac{1}{2}+\dfrac{1}{3}\)

\( S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\).

Kumbuka kwamba kwa masharti mawili ya mwisho katika\( S_4\),

\[ \frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber \]

Kwa hiyo, tunahitimisha kuwa

\[ S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber \]

Kutumia wazo moja kwa\( S_8\), tunaona kwamba

\(\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right)\).

Kutoka kwa mfano huu, tunaona hiyo\( S_1=1, S_2=1+1/2, S_4>1+2(1/2),\) na\( S_8>1+3(1/2)\). Kwa ujumla, inaweza kuonyeshwa kuwa\( S_{2^j}>1+j(1/2)\) kwa wote\( j>1\). Tangu\( 1+j(1/2)→∞,\) sisi kuhitimisha kwamba mlolongo\( {S_k}\) ni unbounded na hivyo hutofautiana. Katika sehemu iliyotangulia, tulisema kuwa utaratibu unaobadilika umepakana. Kwa hiyo, tangu\( {S_k}\) haijulikani, inatofautiana. Hivyo, mfululizo wa harmonic unatofautiana.

Mali ya Algebraic ya Mfululizo wa Convergent

Kwa kuwa jumla ya mfululizo convergent usio hufafanuliwa kama kikomo cha mlolongo, mali algebraic kwa mfululizo hapa chini kufuata moja kwa moja kutoka mali algebraic kwa Utaratibu.

Kumbuka\(\PageIndex{1}\): Algebraic Properties of Convergent Series

Hebu\(\displaystyle \sum_{n=1}^∞ a_n\) na\(\displaystyle \sum_{n=1}^∞ b_n\) kuwa mfululizo convergent. Kisha mali zifuatazo za algebraic zinashikilia.

i. mfululizo\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) hujiunga, na\(\displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n.\) (Sum Utawala)

ii. Mfululizo\(\displaystyle \sum_{n=1}^∞(a_n−b_n)\) hujiunga, na\(\displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n.\) (Utawala wa Tofauti)

iii. Kwa idadi yoyote halisi\( c\), mfululizo\(\displaystyle \sum_{n=1}^∞ca_n\) hujiunga, na\(\displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n\). (Utawala wa Mara nyingi)

Mfano\( \PageIndex{2}\): Using Algebraic Properties of Convergent Series

Tathmini\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].\)

Suluhisho

Sisi ilionyesha mapema kwamba

\[ \sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber \]

na

\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber \]

Kwa kuwa wote wa mfululizo huo hujiunga, tunaweza kutumia mali ya Kumbuka\(\PageIndex{1}\) kutathmini

\[\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber \]

Kutumia utawala wa jumla, andika

\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.\)

Kisha, kwa kutumia utawala wa mara kwa mara na kiasi hapo juu, tunaweza kuhitimisha kwamba

\(\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.\)

Zoezi\(\PageIndex{2}\)

Tathmini\(\displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}\).

Kidokezo

Andika upya kama\(\displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}\).

Jibu

10

Kijiometri Series

Mfululizo wa kijiometri ni mfululizo wowote ambao tunaweza kuandika kwa fomu

\[ a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber \]

Kwa sababu uwiano wa kila neno katika mfululizo huu kwa muda uliopita ni r, idadi r inaitwa uwiano. Sisi rejea kama mrefu ya awali kwa sababu ni mrefu ya kwanza katika mfululizo. Kwa mfano, mfululizo

\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber \]

ni mfululizo wa kijiometri na muda wa awali\( a=1\) na uwiano\( r=1/2\).

Kwa ujumla, mfululizo wa kijiometri hujiunga lini? Fikiria mfululizo wa kijiometri

\[\sum_{n=1}^∞ar^{n−1} \nonumber \]

lini\( a>0\). Mlolongo wake wa kiasi cha sehemu\( {S_k}\) hutolewa na

\[S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber \]

Fikiria kesi wakati\( r=1.\) Katika kesi hiyo,

\[S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber \]

tangu\( a>0\), tunajua\( ak→∞\) kama\( k→∞\). Kwa hiyo, mlolongo wa kiasi cha sehemu ni unbounded na hivyo hutofautiana. Kwa hiyo, mfululizo usio na kipimo unatofautiana\( r=1\). Kwa\( r≠1\), kupata kikomo cha\( {S_k}\), kuzidisha Equation na\( 1−r\). Kufanya hivyo, tunaona kwamba

\[ (1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber \]

Masharti mengine yote kufuta nje.

Kwa hiyo,

\( S_k=\dfrac{a(1−r^k)}{1−r}\)kwa\( r≠1\).

Kutoka majadiliano yetu katika sehemu ya awali, tunajua kwamba mlolongo kijiometri\( r^k→0\) kama\( |r|<1\) na kwamba\( r^k\) diverges kama\( |r|>1\) au\( r=±1\). Kwa hiyo, kwa\( |r|<1, S_k→\dfrac{a}{1−r}\) na tuna

\[ \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber \]

Kama\( |r|≥1, S_k\) diverges, na kwa hiyo

\[ \sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber \]

Ufafanuzi: Mfululizo wa Kugeuka na Kubadilisha

Mfululizo wa kijiometri ni mfululizo wa fomu

\[\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \nonumber \]

Ikiwa\( |r|<1\), mfululizo hujiunga, na

\[\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber \]

Ikiwa\( |r|≥1\), mfululizo hupungua.

Mfululizo wa kijiometri wakati mwingine huonekana kwa aina tofauti kidogo. Kwa mfano, wakati mwingine index huanza katika thamani zaidi ya\( n=1\) au exponent inahusisha kujieleza linear kwa\( n\) zaidi ya\( n−1\). Muda mrefu kama tunaweza kuandika upya mfululizo katika fomu iliyotolewa na Equation, ni mfululizo wa kijiometri. Kwa mfano, fikiria mfululizo

\[\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber \]

Ili kuona kwamba hii ni mfululizo wa kijiometri, tunaandika maneno kadhaa ya kwanza:

\(\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.\)

Tunaona kwamba muda wa awali ni\( a=4/9\) na uwiano ni\( r=2/3.\) Kwa hiyo, mfululizo unaweza kuandikwa kama

\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.\)

Tangu\( r=2/3<1\), mfululizo huu unajiunga, na jumla yake hutolewa na

\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.\)

Mfano\( \PageIndex{3}\): Determining Convergence or Divergence of a Geometric Series

Kuamua kama kila mfululizo wa kijiometri zifuatazo hujiunga au hupungua, na ikiwa hujiunga, pata jumla yake.

1. \(\displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}\)
2. \(\displaystyle \sum^∞_{n=1}e^{2n}\)

Suluhisho

a Kuandika maneno kadhaa ya kwanza katika mfululizo, tuna

\[\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}\]

Muda wa awali\( a=−3\) na uwiano\( r=−3/4\). Tangu\( |r|=3/4<1\), mfululizo hujiunga

\[ \frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber \]

b Kuandika mfululizo huu kama

\[ e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber \]

tunaweza kuona kwamba hii ni mfululizo kijiometri ambapo\( r=e^2>1.\) Kwa hiyo, mfululizo diverges.

Zoezi\(\PageIndex{3}\)

Kuamua kama mfululizo\(\displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1}\) hujiunga au hupungua. Ikiwa inageuka, pata jumla yake.

Kidokezo

\( r=−2/5\)

Jibu

\( 5/7\)

Sasa tunageuka mawazo yetu kwa matumizi mazuri ya mfululizo wa kijiometri. Tunaonyesha jinsi zinaweza kutumiwa kuandika decimals kurudia kama sehemu ndogo za integers.

Mfano\( \PageIndex{4}\): Writing Repeating Decimals as Fractions of Integers

Tumia mfululizo wa kijiometri kuandika\( 3.\bar{26}\) kama sehemu ya integers.

Suluhisho

Tangu\( 3.\bar{26}—=3.262626…,\) kwanza tunaandika

\[\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{1000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}\]

Kupuuza neno 3, mapumziko ya maneno haya ni mfululizo wa kijiometri na muda wa awali\( a=26/10^2\) na uwiano\( r=1/10^2.\) Kwa hiyo, jumla ya mfululizo huu ni

\[ \frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber \]

Hivyo,

\( 3.262626…=3+\frac{26}{99}=\frac{323}{99}\).

Zoezi\(\PageIndex{4}\)

Andika\( 5.2\bar{7}\) kama sehemu ya integers.

Kidokezo

Kwa kuelezea nambari hii kama mfululizo, pata mfululizo wa kijiometri na muda wa awali\( a=7/100\) na uwiano\( r=1/10\).

Jibu

\( 475/90\)

Mfano\( \PageIndex{5}\): Finding the Area of the Koch Snowflake

Kufafanua mlolongo wa takwimu\( \{F_n\}\) recursively kama ifuatavyo (Kielelezo\(\PageIndex{2}\)). Hebu\( F_0\) kuwa pembetatu ya equilateral na pande za urefu\( 1\). Kwa\( n≥1\), basi\( F_n\) kuwa Curve kuundwa kwa kuondoa tatu katikati ya kila upande wa\( F_{n−1}\) na kuchukua nafasi yake kwa pembetatu equilateral akizungumzia nje. Takwimu ya kikwazo kama\( n→∞\) inajulikana kama theluji ya Koch.

Kielelezo\(\PageIndex{2}\): Takwimu nne za kwanza\( F_3\),, na, katika ujenzi wa theluji ya Koch.\( F_0,F_1,F_2\)

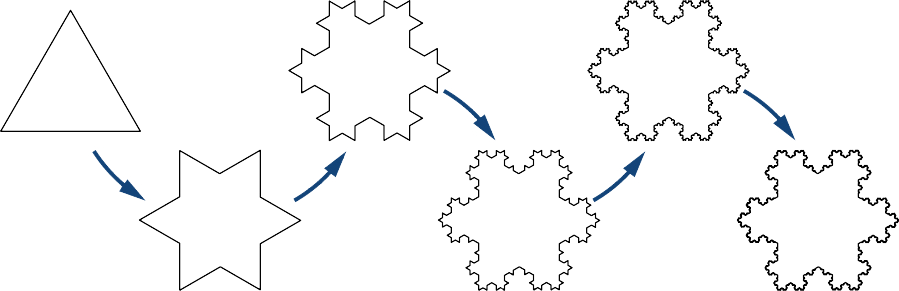
1. Kupata urefu\( L_n\) wa mzunguko wa\( F_n\). Tathmini\(\displaystyle \lim_{n→∞}L_n\) ili kupata urefu wa mzunguko wa theluji ya Koch.
2. Pata eneo\( A_n\) la takwimu\( F_n\). Tathmini\(\displaystyle \lim_{n→∞}A_n\) ili kupata eneo la theluji la Koch.

Suluhisho

Hebu\( N_n\) kuashiria idadi ya pande za takwimu\( F_n\). Tangu\( F_0\) ni pembetatu,\( N_0=3\). Hebu juu ya kuashiria urefu wa kila upande wa\( F_n\). Kwa kuwa\( F_0\) ni pembetatu ya equilateral na pande za urefu\( l_0=1\), sasa tunahitaji kuamua\( N_1\) na\( l_1\). Tangu\( F_1\) ni kuundwa kwa kuondoa tatu katikati ya kila upande na kuchukua nafasi ya kwamba sehemu line na makundi mawili line, kwa kila upande wa\( F_0\), sisi kupata pande nne katika\( F_1\). Kwa hiyo, idadi ya pande kwa\( F_1\) ni

\( N_1=4⋅3\).

Kwa kuwa urefu wa kila moja ya makundi haya\( 1/3\) mapya ya mstari ni urefu wa makundi ya mstari ndani\( F_0\), urefu wa makundi ya mstari\( F_1\) hutolewa na

\( l_1=\frac{1}{3}⋅1=\frac{1}{3}\).

Vile vile\( F_2\), kwa, tangu katikati ya tatu ya kila upande wa\( F_1\) ni kuondolewa na kubadilishwa na makundi mawili ya mstari, idadi ya pande\( F_2\) hutolewa na

\( N_2=4N_1=4(4⋅3)=4^2⋅3.\)

Kwa kuwa urefu wa kila pande hizi ni urefu\( 1/3\) wa pande za\( F_1\), urefu wa kila upande wa takwimu\( F_2\) hutolewa na

\( l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2\).

Zaidi kwa ujumla, tangu\( F_n\) ni kuundwa kwa kuondoa tatu katikati ya kila upande wa\( F_{n−1}\) na kuchukua nafasi ya kwamba sehemu line na makundi mawili ya mstari wa urefu\( \frac{1}{3}l_{n−1}\) katika sura ya pembetatu equilateral, tunajua kwamba\( N_n=4N_{n−1}\) na\( l_n=\dfrac{l_{n−1}}{3}\). Kwa hiyo, idadi ya pande za takwimu\( F_n\) ni

\( N_n=4^n⋅3\)

na urefu wa kila upande ni

\[ l_n=\left(\frac{1}{3}\right)^n. \nonumber \]

Kwa hiyo, kuhesabu mzunguko wa\( F_n\), tunazidisha idadi ya pande\( N_n\) na urefu wa kila upande\( l_n\). Tunahitimisha kuwa mzunguko wa\( F_n\) hutolewa na

\[ L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber \]

Kwa hiyo, urefu wa mzunguko wa theluji ya Koch ni

\[ L=\lim_{n→∞}L_n=∞. \nonumber \]

b Hebu\( T_n\) kutaja eneo la kila pembetatu mpya iliyoundwa wakati wa kutengeneza\( F_n\). Kwa maana\( n=0, T_0\) ni eneo la pembetatu ya awali ya equilateral. Kwa hiyo,\( T_0=A_0=\sqrt{3}/4\). Kwa\( n≥1\), tangu urefu wa pande ya pembetatu mpya ni urefu\( 1/3\) wa pande za\( F_{n−1}\), tuna

\[ T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber \]

Kwa hiyo,\( T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}\). Tangu pembetatu mpya ni sumu kila upande wa\( F_{n−1}\),

\[ A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber \]

Kuandika maneno machache ya kwanza\( A_0,A_1,A_2,\) tunaona kwamba

\( A_0=\frac{\sqrt{3}}{4}\)

\(A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]\)

\( A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2]\).

Kwa ujumla zaidi,

\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right]\).

Factoring\( 4/9\) nje ya kila neno ndani ya mabano ya ndani, sisi rewrite kujieleza yetu kama

\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right]\).

Maneno\( 1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\) ni jumla ya kijiometri. Kama inavyoonekana hapo awali, jumla hii satisfies

\( 1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.\)

Kubadilisha maneno haya katika maneno hapo juu na kurahisisha, tunahitimisha kuwa

\[ A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber \]

Kwa hiyo, eneo la theluji la Koch ni

\(\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.\)

Uchambuzi

Snowflake ya Koch inavutia kwa sababu ina eneo la mwisho, lakini mzunguko usio na kipimo. Ingawa kwa mara ya kwanza hii inaweza kuonekana haiwezekani, kumbuka kwamba umeona mifano sawa mapema katika maandiko. Kwa mfano, fikiria kanda iliyopakana na Curve\( y=1/x^2\) na\( x\) -axis juu ya muda\( [1,∞).\) Tangu muhimu yasiyofaa

\[ ∫^∞_1\frac{1}{x^2}\,dx \nonumber \]

hujiunga, eneo la mkoa huu ni wa mwisho, ingawa mzunguko hauwezi.

Telescoping mfululizo

Fikiria mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\) Tulijadili mfululizo huu katika Mfano, kuonyesha kwamba mfululizo hujiunga kwa kuandika kiasi cha kwanza cha sehemu kadhaa\( S_1,S_2,…,S_6\) na kutambua kwamba wote ni fomu\( S_k=\dfrac{k}{k+1}\). Hapa tunatumia mbinu tofauti kuonyesha kwamba mfululizo huu hujiunga. Kwa kutumia sehemu ndogo, tunaweza kuandika

\[ \frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber \]

Kwa hiyo, mfululizo unaweza kuandikwa kama

\(\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1+\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.\)

Kuandika nje ya kwanza maneno kadhaa katika mlolongo wa kiasi cha sehemu\( {S_k},\) tunaona kwamba

\( S_1=1−\frac{1}{2}\)

\( S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}\)

\( S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}\).

Kwa ujumla,

\( S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}\).

Tunaona kwamba maneno ya kati yanaghairi nje, na kuacha tu masharti ya kwanza na ya mwisho. Kwa maana, mfululizo huanguka kama spyglass yenye mirija ambayo hupotea ndani ya kila mmoja ili kufupisha darubini. Kwa sababu hii, tunaita mfululizo ambao una mali hii mfululizo wa darubini. Kwa mfululizo huu, tangu\( S_k=1−1/(k+1)\) na\( 1/(k+1)→0\) kama\( k→∞\), mlolongo wa kiasi cha sehemu hujiunga na\( 1\), na kwa hiyo mfululizo hujiunga na\( 1\).

Ufafanuzi

Mfululizo wa darubini ni mfululizo ambao maneno mengi yanaghairi katika kila moja ya jumla ya sehemu, na kuacha baadhi tu ya masharti ya kwanza na baadhi ya masharti ya mwisho.

Kwa mfano, mfululizo wowote wa fomu

\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯\)

ni mfululizo wa darubini. Tunaweza kuona hili kwa kuandika baadhi ya kiasi cha sehemu. Hasa, tunaona kwamba

\( S_1=b_1−b_2\)

\( S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3\)

\( S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.\)

Kwa ujumla, jumla ya sehemu ya mfululizo huu ni

\( S_k=b_1−b_{k+1}\).

Kwa kuwa jumla ya sehemu ya kth inaweza kuwa rahisi kwa tofauti ya maneno haya mawili, mlolongo wa kiasi cha sehemu\( {S_k}\) utaungana ikiwa na tu ikiwa mlolongo\( {b_{k+1}}\) unajiunga. Zaidi ya hayo, ikiwa mlolongo\( b_{k+1}\) unajiunga na idadi fulani ya mwisho B, basi mlolongo wa kiasi cha sehemu hujiunga na\( b_1−B\), na kwa hiyo

\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.\)

Katika mfano unaofuata, tunaonyesha jinsi ya kutumia mawazo haya kuchambua mfululizo wa darubini wa fomu hii.

Mfano\( \PageIndex{6}\): Evaluating a Telescoping Series

Kuamua kama mfululizo telescoping

\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]\)

hujiunga au hupungua. Ikiwa inageuka, pata jumla yake.

Suluhisho

Kwa kuandika maneno katika mlolongo wa kiasi cha sehemu, tunaweza kuona kwamba

\( S_1=\cos(1)−\cos(\frac{1}{2})\)

\( S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})\)

\( S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))\)

\( =\cos(1)−\cos(\frac{1}{4})\).

Kwa ujumla,

\( S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right)\).

Tangu\( 1/(k+1)→0\) kama\( k→∞\) na\( \cos x\) ni kazi ya kuendelea,\( \cos(1/(k+1))→\cos(0)=1\). Kwa hiyo, tunahitimisha hilo\( S_k→\cos(1)−1\). Mfululizo wa darubini hujiunga na jumla hutolewa na

\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.\)

Zoezi\(\PageIndex{5}\)

Kuamua kama\(\displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}]\) converges au diverges. Ikiwa inageuka, pata jumla yake.

Kidokezo

Andika mlolongo wa kiasi cha sehemu ili uone ni maneno gani ya kufuta.

Jibu

\( e−1\)

Mara kwa mara ya Euler

Tumeonyesha kuwa mfululizo harmonic\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverges. Hapa sisi kuchunguza tabia ya kiasi sehemu\( S_k\) kama\( k→∞.\) Hasa, sisi kuonyesha kwamba wao kuishi kama asili logarithm kazi kwa kuonyesha kwamba kuna mara kwa mara\( γ\) kama kwamba

\(\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ\)kama\( k→∞.\)

Mara kwa mara hii\( γ\) inajulikana kama mara kwa mara ya Euler.

1. Hebu\(\displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right).\) Tathmini\( T_k\) kwa maadili mbalimbali ya\( k\).

2. Kwa\( T_k\) kama inavyoelezwa katika sehemu 1. kuonyesha kwamba mlolongo\( {T_k}\) hujiunga kwa kutumia hatua zifuatazo.

Onyesha kwamba mlolongo\( {T_k}\) ni monotone kupungua. (Kidokezo: Onyesha hilo\( \ln(1+1/k>1/(k+1))\)

Onyesha kwamba mlolongo\( {T_k}\) umepakana chini na sifuri. (Kidokezo: Express\( \ln k\) kama muhimu ya uhakika.)

c Tumia Theorem ya Muungano wa Monotone ili kuhitimisha kuwa mlolongo\( {T_k}\) hujiunga. Kikomo\( γ\) ni mara kwa mara ya Euler.

3. Sasa makisio jinsi mbali\( T_k\) ni kutoka\( γ\) kwa integer fulani\( k\). Thibitisha kwamba\( k≥1, 0<T_k−γ≤1/k\) kwa kutumia hatua zifuatazo.

Onyesha kwamba\( \ln(k+1)−\ln k<1/k.\)

b Tumia matokeo kutoka kwa sehemu a. ili kuonyesha kwamba kwa integer yoyote\( k\),

\[ T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber \]

c Kwa integers yoyote\( k\) na\( j\) vile kwamba\( j>k\), kueleza\( T_k−T_j\) kama jumla ya darubini kwa kuandika

\[ T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber \]

Tumia matokeo kutoka kwa sehemu ya b. pamoja na jumla hii ya darubini ili kuhitimisha kwamba

\[ T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber \]

a. kutumia kikomo kwa pande zote mbili za kukosekana kwa usawa katika sehemu c. kuhitimisha kwamba

\[ T_k−γ≤\frac{1}{k}. \nonumber \]

e Makadirio\( γ\) ya usahihi wa ndani ya 0.001.

---

Dhana muhimu

• Kutokana na mfululizo usio

\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯\)

na mlolongo sambamba ya kiasi sehemu\( {S_k}\) ambapo

\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\),

mfululizo hujiunga ikiwa na tu ikiwa mlolongo\( {S_k}\) unajiunga.

• Mfululizo wa kijiometri\(\displaystyle \sum^∞_{n=1}ar^{n−1}\) hujiunga ikiwa\( |r|<1\) na hutofautiana ikiwa\( |r|≥1.\) Kwa\( |r|<1,\)

\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\).

• mfululizo harmonic

\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)

hutengana.

• Mfululizo wa fomu\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯\) ni mfululizo wa darubini. Jumla ya\( k^{\text{th}}\) sehemu ya mfululizo huu hutolewa na\( S_k=b_1−b_{k+1}\). Mfululizo utaungana ikiwa na tu ikiwa\(\displaystyle \lim_{k→∞} b_{k+1}\) ipo. Katika kesi hiyo,

\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1})\).

Mlinganyo muhimu

• Harmonic mfululizo

\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)

• Jumla ya mfululizo wa kijiometri

\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\)kwa\( |r|<1\)

---

faharasa

muunganiko wa mfululizo

mfululizo hujiunga ikiwa mlolongo wa kiasi cha sehemu ya mfululizo huo hujiunga

tofauti ya mfululizo

mfululizo diverges kama mlolongo wa kiasi sehemu ya kwamba mfululizo diverges

mfululizo wa kijiometri

mfululizo wa kijiometri ni mfululizo ambao unaweza kuandikwa kwa fomu

\(\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯\)

mfululizo harmonic

mfululizo wa harmonic unachukua fomu

\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)

mfululizo usio na mwisho

mfululizo usio na mwisho ni usemi wa fomu

\(\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n\)

jumla ya sehemu

jumla ya\( kth\) sehemu ya mfululizo usio na mwisho\(\displaystyle \sum^∞_{n=1}a_n\) ni jumla ya mwisho

\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\)

telescoping mfululizo

mfululizo wa telescoping ni moja ambayo wengi wa maneno kufuta katika kila moja ya kiasi cha sehemu