9.1E: Mazoezi ya Sehemu ya 9.1

Last updated
Save as PDF

Page ID: 178899

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 4, pata masharti sita ya kwanza ya kila mlolongo, kuanzia na$ n=1$.

1)$a_n=1+(−1)^n$ kwa$ n≥1$

Jibu: $ a_n=0$ikiwa$ n$ ni isiyo ya kawaida na$ a_n=2$ ikiwa$ n$ ni hata

2)$ a_n=n^2−1$ kwa$ n≥1$

3)$ a_1=1$ na$ a_n=a_{n−1}+n$ kwa$ n≥2$

Jibu: $ {a_n}={1,3,6,10,15,21,…}$

4)$ a_1=1, a_2=1$ na$ a_n+2=a_n+a_{n+1}$ kwa$ n≥1$

5) Pata formula wazi kwa$ a_n$ wapi$ a_1=1$ na$ a_n=a_{n−1}+n$ kwa$ n≥2$.

Jibu: $ a_n=\dfrac{n(n+1)}{2}$

6) Pata fomu$ a_n$ kwa$n^{\text{th}}$ muda wa mlolongo wa hesabu ambao muda wake wa kwanza ni$ a_1=1$ kama huo$ a_{n−1}−a_n=17$$ n≥1$.

7) Pata fomu$ a_n$ kwa$n^{\text{th}}$ muda wa mlolongo wa hesabu ambao muda wake wa kwanza ni$ a_1=−3$ kama huo$ a_{n−1}−a_n=4$$ n≥1$.

Jibu: $ a_n=4n−7$

8) Pata fomu$ a_n$ kwa$n^{\text{th}}$ muda wa mlolongo wa kijiometri ambao muda wake wa kwanza ni$ a_1=1$ kama huo$ n≥1$.$ \dfrac{a_{n+1}}{a_n}=10$

9) Pata fomu$ a_n$ kwa$n^{\text{th}}$ muda wa mlolongo wa kijiometri ambao muda wake wa kwanza ni$ a_1=3$ kama huo$ n≥1$.$ \dfrac{a_{n+1}}{a_n}=1/10$

Jibu: $ a_n=3.10^{1−n}=30.10^{−n}$

10) Kupata formula wazi kwa$n^{\text{th}}$ muda wa mlolongo ambao kwanza maneno kadhaa ni$ {0,3,8,15,24,35,48,63,80,99,…}.$ (kidokezo: Kwanza kuongeza moja kwa kila neno.)

11) Kupata formula wazi kwa$n^{\text{th}}$ muda wa mlolongo kuridhisha$ a_1=0$ na$ a_n=2a_{n−1}+1$ kwa$ n≥2$.

Jibu: $ a_n=2^n−1$

Katika mazoezi 12 na 13, tafuta formula kwa muda wa jumla$ a_n$ wa kila moja ya utaratibu wafuatayo.

12)$ {1,0,−1,0,1,0,−1,0,…}$ (dokezo: Kupata ambapo$\sin x$ inachukua maadili haya)

13)$ {1,−1/3,1/5,−1/7,…}$

Jibu: $ a_n=\dfrac{(−1)^{n−1}}{2n−1}$

Katika mazoezi 14-18, kupata kazi$ f(n)$ ambayo kubainisha$n^{\text{th}}$ mrefu$ a_n$ ya yafuatayo Utaratibu recursively defined, kama$ a_n=f(n)$.

14)$ a_1=1$ na$ a_{n+1}=−a_n$ kwa$ n≥1$

15)$ a_1=2$ na$ a_{n+1}=2a_n$ kwa$ n≥1$

Jibu: $ f(n)=2^n$

16)$ a_1=1$ na$ a_{n+1}=(n+1)a_n$ kwa$ n≥1$

17)$ a_1=2$ na$ a_{n+1}=(n+1)a_n/2$ kwa$ n≥1$

Jibu: $f(n)=\dfrac{n!}{2^{n-2}}$

18)$ a_1=1$ na$ a_{n+1}=a_n/2^n$ kwa$ n≥1$

Katika mazoezi 19 - 22, njama$ N$ masharti ya kwanza ya mlolongo uliopewa. Hali kama ushahidi wa graphical unaonyesha kwamba mlolongo hujiunga au hupungua.

19) [T]$ a_1=1, a_2=2$, na kwa$ n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2})$;$ N=30$

Jibu

Masharti oscillate juu$ 5/3$ na chini na kuonekana kuungana na$ 5/3$.

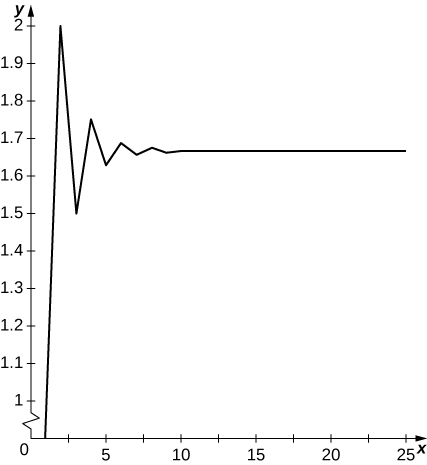
20) [T]$ a_1=1, a_2=2, a_3=3$ na kwa$ n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30$

21) [T]$ a_1=1, a_2=2$, na kwa$ n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30$

Jibu

Masharti oscillate juu$ y≈1.57..$ na chini na kuonekana kugeuka na kikomo.

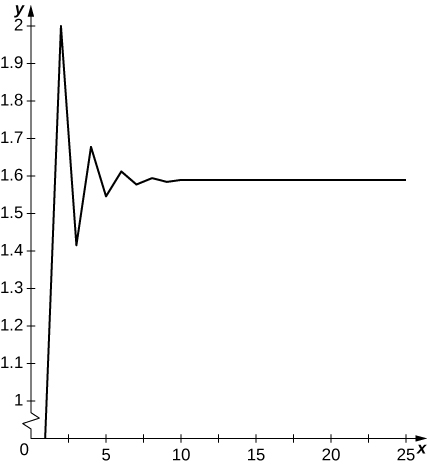
22) [T]$ a_1=1, a_2=2, a_3=3$, na kwa$ n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30$

Katika mazoezi 23 - 16, tuseme kwamba$\displaystyle \lim_{n→∞}a_n=1, $$\displaystyle \lim_{n→∞}b_n=−1$, na$ 0<−b_n<a_n$ kwa wote$ n$.

Kutumia habari hii, tathmini kila moja ya mipaka ifuatayo, sema kuwa kikomo haipo, au sema kuwa hakuna habari za kutosha ili kuamua kama kikomo kipo.

23)$\displaystyle \lim_{n→∞}3a_n−4b_n$

Jibu: $\displaystyle \lim_{n→∞}3a_n−4b_n \quad = \quad 7$

24)$\displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n$

25)$\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}$

Jibu: $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n} \quad = \quad 0$

26)$\displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}$

Katika mazoezi 27 - 30, pata kikomo cha kila moja ya utaratibu wafuatayo, ukitumia utawala wa L'Hôpital wakati unaofaa.

27)$ \dfrac{n^2}{2^n}$

Jibu: $\displaystyle \lim_{n→∞} \dfrac{n^2}{2^n} \quad = \quad 0$

28)$ \dfrac{(n−1)^2}{(n+1)^2}$

29)$ \dfrac{\sqrt{n}}{\sqrt{n+1}}$

Jibu: $\displaystyle \lim_{n→∞} \dfrac{\sqrt{n}}{\sqrt{n+1}} \quad = \quad 1 $

30)$ n^{1/n}$ (Kidokezo:$ n^{1/n}=e^{\frac{1}{n}\ln n})$

Katika mazoezi 31 - 37, sema kama kila mlolongo umepakana na ikiwa hatimaye ni monotone, kuongezeka, au kupungua.

31)$ n/2^n, n≥2$

Jibu: imepakana, kupungua kwa$ n≥1$

32)$ \ln\left(1+\dfrac{1}{n}\right)$

33)$ \sin n$

Jibu: imefungwa, si monotone

34)$ \cos(n^2)$

35)$ n^{1/n}, \quad n≥3$

Jibu: imepakana, kupungua

36)$ n^{−1/n}, \quad n≥3$

37)$ \tan n$

Jibu: si monotone, si imepakana

Katika mazoezi 38 - 39, onyesha kama mlolongo uliopewa una kikomo. Ikiwa inafanya, pata kikomo.

38)$ a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}}$ nk.

39)$ a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….$

Jibu: $ a_n$ni kupungua na imepakana chini na$2$. kikomo a lazima kukidhi$ a=\sqrt{2a}$ hivyo$ a=2$, huru ya thamani ya awali.

Tumia Theorem itapunguza ili kupata kikomo cha kila mlolongo katika mazoezi 40 - 43.

40)$ n\sin(1/n)$

41)$ \dfrac{\cos(1/n)−1}{1/n}$

Jibu: $0$

42)$ a_n=\dfrac{n!}{n^n}$

43)$ a_n=\sin n \sin(1/n)$

Jibu: $ 0$tangu$|\sin x|≤|x|$ na$ |\sin x|≤1$ hivyo$ −\dfrac{1}{n}≤a_n≤\dfrac{1}{n})$.

Kwa utaratibu katika mazoezi 44 na 45, njama$ 25$ masharti ya kwanza ya mlolongo na ueleze kama ushahidi wa kielelezo unaonyesha kwamba mlolongo hujiunga au hutofautiana.

44) [T]$ a_n=\sin n$

45) [T]$ a_n=\cos n$

Jibu

Grafu oscillates na unaonyesha hakuna kikomo.

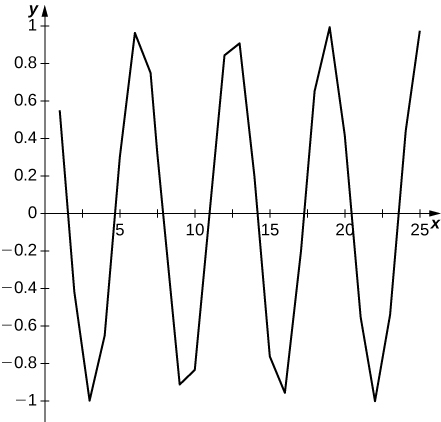
Katika mazoezi 46 - 52, tambua kikomo cha mlolongo au uonyeshe kwamba mlolongo unatofautiana. Ikiwa inageuka, pata kikomo chake.

46)$ a_n=\tan^{−1}(n^2)$

47)$ a_n=(2n)^{1/n}−n^{1/n}$

Jibu: $ n^{1/n}→1$na$ 2^{1/n}→1,$ hivyo$ a_n→0$

48)$ a_n=\dfrac{\ln(n^2)}{\ln(2n)}$

49)$ a_n=\left(1−\frac{2}{n}\right)^n$

Jibu: Tangu$ (1+1/n)^n→e$, moja ina$ (1−2/n)^n≈(1+k)^{−2k}→e^{−2}$ kama$ k→∞.$

50)$ a_n=\ln\left(\dfrac{n+2}{n^2−3}\right)$

51)$ a_n=\dfrac{2^n+3^n}{4^n}$

Jibu: $ 2^n+3^n≤2⋅3^n$na$ 3^n/4^n→0$ kama$ n→∞$,$ a_n→0$ ili$ n→∞.$

52)$ a_n=\dfrac{(1000)^n}{n!}$

53)$ a_n=\dfrac{(n!)^2}{(2n)!}$

Jibu: $ \dfrac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\dfrac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n$. Hasa$ a_{n+1}/a_n≤1/2$, hivyo$ a_n→0$ kama$ n→∞$.

Mbinu Newton inataka takriban ufumbuzi$ f(x)=0$ unaoanza na makadirio ya awali$ x_0$ na mfululizo amefafanua mlolongo$ x_{n+1}=x_n−\dfrac{f(x_n)}{f′(x_n)}$. Kwa uchaguzi uliotolewa$ f$ na$ x_0$, andika formula kwa$ x_{n+1}$. Ikiwa mlolongo unaonekana kugeuka, fanya fomu halisi ya suluhisho$ x$, kisha utambue kikomo$ x$ sahihi kwa maeneo manne ya decimal na ndogo zaidi ambayo$ n$$ x_n$ inakubaliana na$ x$ sehemu nne za decimal.

54) [T]$ f(x)=x^2−2,\quad x_0=1$

55) [T]$ f(x)=(x−1)^2−2,\quad x_0=2$

Jibu: \ (x_ {n+1} =x_n- (x_n-1) ^2,12) /2 (x_n-1);\;
x=1+\ sqrt {2},\; x≈ 2.4142,\; n = 5\)

56) [T]$ f(x)=e^x−2, \quad x_0=1$

57) [T]$ f(x)=\ln x−1,\quad x_0=2$

Jibu: \ (x_ {n+1} =x_n-x_n (\ ln (x_n) -1);\;
x=e,\; x≈ 2.7183,\; n = 5\)

58) [T] Tuseme kuanza na lita moja ya siki na uondoe mara kwa mara$0.1$ L, badala ya maji, kuchanganya, na kurudia.

Pata fomu ya mkusanyiko baada ya$ n$ hatua.

b Baada ya hatua ngapi mchanganyiko una chini ya$ 10\%$ siki?

59) [T] Ziwa mwanzoni lina$ 2000$ samaki. Tuseme kwamba kwa kutokuwepo kwa wadudu au sababu nyingine za kuondolewa, idadi ya samaki huongezeka kwa$ 6\%$ kila mwezi. Hata hivyo, kuzingatia sababu zote,$ 150$ samaki hupotea kila mwezi.

Eleza kwa nini idadi ya samaki baada ya$ n$ miezi inatokana$ P_n=1.06P_{n−1}−150$ na kwa$ P_0=2000$.

b Ni samaki wangapi watakuwa katika bwawa baada ya mwaka mmoja?

Jibu: bila hasara, idadi ya watu bila kutii$ P_n=1.06P_{n−1}$. Kuondoa$ 150$ akaunti kwa hasara za samaki.
b Baada ya$ 12$ miezi, tuna$ P_{12}≈1494.$

60) [T] Akaunti ya benki chuma$ 5\%$ riba imezungukwa kila mwezi. Tuseme$ $1000$ kwamba awali zilizoingia katika akaunti, lakini hiyo$ $10$ ni kuondolewa kila mwezi.

Onyesha kwamba kiasi katika akaunti baada ya$ n$ miezi ni$ A_n=(1+.05/12)A_{n−1}−10; \; A_0=1000.$

b Ni kiasi gani cha fedha kitakuwa katika akaunti baada ya$ 1$ mwaka?

c Je! Kiasi kinaongezeka au kupungua?

tuseme kwamba badala ya$ $10$, fasta kiasi$ d$ dola ni kuondolewa kila mwezi. Pata thamani ya kiasi$ d$ hicho katika akaunti baada ya kila mwezi kinabakia$ $1000$.

e Ni nini kinachotokea ikiwa$ d$ ni kubwa kuliko kiasi hiki?

61) [T] Mwanafunzi huchukua mkopo wa$ $10,000$ chuo cha kwa kiwango cha asilimia ya kila mwaka ya$ 6\%,$ imezungukwa kila mwezi.

a Kama mwanafunzi anafanya malipo ya$ $100$ mwezi, ni kiasi gani mwanafunzi anadaiwa baada ya$ 12$ miezi?

b Baada ya miezi ngapi mkopo kulipwa mbali?

Jibu: a. mwanafunzi amepata$ $9383$ baada ya$ 12$ miezi.
b. mkopo italipwa katika kamili baada ya$ 139$ miezi au miaka kumi na moja na nusu.

62) [T] Fikiria mfululizo unaochanganya ukuaji wa kijiometri na kupungua kwa hesabu. Hebu$ a_1=1$. Kurekebisha$ a>1$ na$ 0<b<a$. Kuweka$ a_{n+1}=a.a_n−b.$ Kupata formula kwa$ a_{n+1}$ katika suala la$ a_n, a$,$ b$ na na uhusiano kati$ a$ na$ b$ vile kwamba$ a_n$ hujiunga.

63) [T] uwakilishi binary$ x=0.b_1b_2b_3...$ ya idadi$ x$ kati$ 0$ na$ 1$ inaweza kuelezwa kama ifuatavyo. Hebu$ b_1=0$ kama$ x<1/2$ na$ b_1=1$ kama$ 1/2≤x<1.$ Hebu$ x_1=2x−b_1$. Hebu$ b_2=0$ kama$ x_1<1/2$ na$ b_2=1$ kama$ 1/2≤x<1$. Hebu$ x_2=2x_1−b_2$ na kwa ujumla,$ x_n=2x_{n−1}−b_n$ na$ b_{n−}1=0$ kama$ x_n<1/2$ na$ b_{n−1}=1$ kama$ 1/2≤x_n<1$. Kupata upanuzi binary ya$ 1/3$.

Jibu: $ b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3,$hivyo mfano unarudia, na$ 1/3=0.010101….$

64) [T] Ili kupata makadirio ya$ π$, kuweka$ a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}$, na, kwa ujumla,$ a_{n+1}=\sqrt{2+a_n}$. Hatimaye, kuweka$ p_n=3.2^n\sqrt{2−a_n}$. Kupata kwanza maneno kumi ya$ p_n$ na kulinganisha maadili kwa$ π$.

Kwa mazoezi mawili yafuatayo, kudhani kuwa una upatikanaji wa programu ya kompyuta au chanzo cha mtandao ambacho kinaweza kuzalisha orodha ya zero na wale wa urefu wowote uliotaka. Jenereta za nambari za Pseudo-random (PRNGs) zina jukumu muhimu katika kuiga kelele za random katika mifumo ya kimwili kwa kuunda utaratibu wa zero na zile zinazoonekana kama matokeo ya kupiga sarafu mara kwa mara. Moja ya aina rahisi ya PRNGs recursively amefafanua random-kuangalia mlolongo wa$ N$ integers$ a_1,a_2,…,a_N$ kwa fixing integers mbili maalum$ (K$$ M$ na kuruhusu$ a_{n+1}$ kuwa salio baada ya kugawa$ K.a_n$ katika$ M$, kisha inajenga mlolongo kidogo ya zero na wale ambao $n^{\text{th}}$mrefu$ b_n$ ni sawa na moja kama$ a_n$ ni isiyo ya kawaida na sawa na sifuri kama$ a_n$ ni hata. Ikiwa bits$ b_n$ ni pseudo-random, basi tabia ya wastani wao$ (b_1+b_2+⋯+b_N)/N$ inapaswa kuwa sawa na tabia ya wastani wa bits kweli nasibu yanayotokana.

65) [T] Kuanzia$ K=16,807$ na$ M=2,147,483,647$, kwa kutumia kumi tofauti kuanzia maadili ya$ a_1$, compute Utaratibu wa bits$ b_n$ hadi$ n=1000,$ na kulinganisha wastani wao kwa kumi Utaratibu huo yanayotokana na jenereta random kidogo.

Jibu: Kwa maadili ya kuanzia, wastani$ a_1=1, a_2=2,…, a_1=10,$ wa bit sambamba mahesabu kwa njia iliyoonyeshwa ni$ 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040,$ na$ 0.4840$. Hapa ni mfano wa wastani kumi sambamba ya masharti ya$ 1000$ bits yanayotokana na jenereta random idadi:$ 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980.$ Hakuna mfano halisi katika aina yoyote ya wastani. Wastani wa nambari ya random yanayotokana$ 0.4860$ na random kati na$ 0.5490$$ 0.0630$, aina mbalimbali, wakati wastani wa PRNG bit mahesabu kati$ 0.4680$ na$ 0.5220$, aina mbalimbali$ 0.0540.$

66) [T] Tafuta$ 1000$ tarakimu za kwanza za$ π$ kutumia programu ya kompyuta au rasilimali ya mtandao. Kujenga mlolongo kidogo$ b_n$ kwa kuruhusu$ b_n=1$ kama$n^{\text{th}}$ tarakimu ya$ π$ ni isiyo ya kawaida na$ b_n=0$ kama$n^{\text{th}}$ tarakimu ya$ π$ ni hata. Compute thamani ya wastani wa$ b_n$ na thamani ya wastani ya$ d_n=|b_{n+1}−b_n|, n=1,...,999.$ Je, mlolongo$ b_n$ kuonekana random? Je, tofauti kati ya mambo mfululizo wa$ b_n$ kuonekana random?