9.1: Utaratibu
- Page ID
- 178895
- Pata formula kwa muda wa jumla wa mlolongo.
- Tumia kikomo cha mlolongo ikiwa ipo.
- Kuamua muunganiko au tofauti ya mlolongo uliopewa.
Katika sehemu hii, tunaanzisha Utaratibu na kufafanua maana gani kwa mlolongo wa kugeuza au kupatanisha. Tunaonyesha jinsi ya kupata mipaka ya utaratibu ambao hujiunga, mara nyingi kwa kutumia mali ya mipaka ya kazi zilizojadiliwa mapema. Tunakaribia sehemu hii na Theorem ya Monotone Convergence, chombo ambacho tunaweza kutumia ili kuthibitisha kwamba aina fulani za Utaratibu hujiunga.
Istilahi ya Utaratibu
Kufanya kazi na mada hii mpya, tunahitaji maneno na ufafanuzi mpya. Kwanza, mlolongo usio na kipimo ni orodha iliyoamriwa ya idadi ya fomu
\[a_1,a_2,a_3,…,a_n,….\nonumber \]
Kila moja ya idadi katika mlolongo inaitwa neno. Ishara\(n\) inaitwa tofauti ya index kwa mlolongo. Tunatumia nukuu
\[\{a_n\}^∞_{n=1},\nonumber \]
au tu\(\{a_n\}\), kuashiria mlolongo huu. Nukuu sawa hutumiwa kwa seti, lakini mlolongo ni orodha iliyoamriwa, wakati seti haijaamriwa. Kwa sababu idadi fulani\(a_n\) ipo kwa kila integer chanya\(n\), tunaweza pia kufafanua mlolongo kama kazi ambao uwanja ni seti ya integers chanya.
Hebu fikiria usio na mwisho, orodha iliyoamriwa
\[2,4,8,16,32,….\nonumber \]
Hii ni mlolongo ambao kwanza, pili, na maneno ya tatu ni kutolewa na\(a_1=2, a_2=4,\) na\(a_3=8.\) Unaweza pengine kuona kwamba maneno katika mlolongo huu na muundo zifuatazo:
\[a_1=2^1,\,a_2=2^2,\,a_3=2^3,\,a_4=2^4 \text{ and } a_5=2^5.\nonumber \]
Kutokana muundo huu inaendelea, tunaweza kuandika\(n^{\text{th}}\) neno katika mlolongo kwa formula wazi\(a_n=2^n.\) Kutumia nukuu hii, tunaweza kuandika mlolongo huu kama
\[\{2^n\}^∞_{n=1}\nonumber \]
au
\[\{2^n\}.\nonumber \]
Vinginevyo, tunaweza kuelezea mlolongo huu kwa njia tofauti. Kwa kuwa kila neno ni mara mbili ya muda uliopita, mlolongo huu unaweza kuelezwa recursively kwa kueleza\(n^{\text{th}}\) neno\(a_n\) katika suala la muda uliopita\(a_{n−1}\). Hasa, tunaweza kufafanua mlolongo huu kama mlolongo\(\{a_n\}\) ambapo\(a_1=2\) na kwa ajili ya wote\(n≥2\), kila neno an hufafanuliwa na uhusiano upprepning
\[a_n=2a_{n−1}. \nonumber \]
Mlolongo usio na kipimo\(\{a_n\}\) ni orodha iliyoamriwa ya idadi ya fomu
\(a_1,\,a_2,\,…,\,a_n,\,….\)
Subscript\(n\) inaitwa tofauti ya index ya mlolongo. Kila idadi\(a_n\) ni muda wa mlolongo. Wakati mwingine Utaratibu hufafanuliwa na formula wazi, katika kesi ambayo\(a_n=f(n)\) kwa baadhi ya kazi\(f(n)\) defined juu integers chanya. Katika hali nyingine, utaratibu hufafanuliwa kwa kutumia uhusiano wa kurudia. Katika uhusiano wa kurudia, neno moja (au zaidi) la mlolongo hutolewa wazi, na maneno yafuatayo yanafafanuliwa kwa suala la maneno ya awali katika mlolongo.
Kumbuka kuwa index haina kuanza saa\(n=1\) lakini inaweza kuanza na integers nyingine. Kwa mfano, mlolongo uliotolewa na formula wazi\(a_n=f(n)\) inaweza kuanza saa\(n=0\), katika hali ambayo mlolongo itakuwa
\[a_0,\,a_1,\,a_2,….\nonumber \]
Vile vile, kwa mlolongo unaofafanuliwa na uhusiano wa kurudia, neno\(a_0\) linaweza kutolewa wazi, na maneno ya\(n≥1\) yanaweza kuelezwa\(a_n\) kwa suala la\(a_{n−1}\). Kwa kuwa mlolongo\(\{a_n\}\) una thamani moja kwa kila integer chanya\(n\), inaweza kuelezewa kama kazi ambayo uwanja wake ni seti ya integers chanya. Matokeo yake, ni busara kujadili grafu ya mlolongo. Grafu ya mlolongo\(\{a_n\}\) lina pointi zote\((n,a_n)\) kwa integers wote chanya n. takwimu inaonyesha graph ya\({2^n}\).
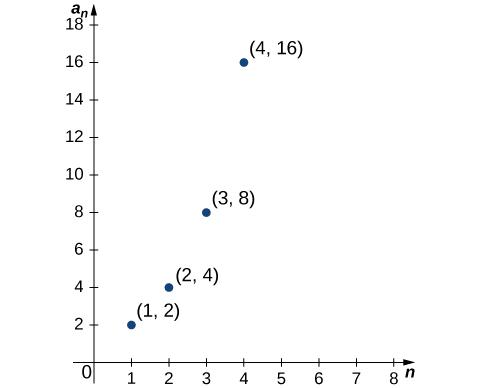
Aina mbili za utaratibu hutokea mara nyingi na hupewa majina maalum: utaratibu wa hesabu na utaratibu wa kijiometri. Katika mlolongo wa hesabu, tofauti kati ya kila jozi ya maneno mfululizo ni sawa. Kwa mfano, fikiria mlolongo
\[3,\,7,\,11,\,15,1\,9, \,\ldots\nonumber \]
Unaweza kuona kwamba tofauti kati ya kila jozi mfululizo wa maneno ni\(4\). Kutokana kwamba muundo huu unaendelea, mlolongo huu ni mlolongo hesabu. Inaweza kuelezewa kwa kutumia uhusiano wa kurudia
\[\begin{cases}a_1=3\\a_n=a_{n−1}+4, \text{ for }\ n≥2\end{cases}.\nonumber \]
Kumbuka kwamba
\[a_2=3+4\nonumber \]
\[a_3=3+4+4=3+2⋅4\nonumber \]
\[a_4=3+4+4+4=3+3⋅4.\nonumber \]
Hivyo, mlolongo unaweza pia kuelezewa kwa kutumia formula wazi.
\[a_n=3+4(n−1)=4n−1.\nonumber \]
Kwa ujumla, mlolongo wa hesabu ni mlolongo wowote wa fomu\(a_n=cn+b.\)
Katika mlolongo wa kijiometri, uwiano wa kila jozi ya maneno mfululizo ni sawa. Kwa mfano, fikiria mlolongo
\[2,\,−\dfrac{2}{3},\,\dfrac{2}{9},\,−\dfrac{2}{27},\,\dfrac{2}{81},….\nonumber \]
Tunaona kwamba uwiano wa muda wowote kwa muda uliopita ni\(−\dfrac{1}{3}\). Kutokana na muundo huu unaendelea, mlolongo huu ni mlolongo wa kijiometri. Inaweza kuelezwa recursively kama
\[ a_1=2\nonumber \]
\[a_n=−\dfrac{1}{3}⋅a_{n−1}, \text{ for }\ n≥2.\nonumber \]
Vinginevyo, tangu
\[ \begin{align*} a_2 &=−\dfrac{1}{3}⋅2 \\[4pt] a_3 &=\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^2⋅2 \\[4pt] a_4 &= \left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^3⋅2,\end{align*} \nonumber \]
tunaona kwamba mlolongo unaweza kuelezewa kwa kutumia formula wazi
\[a_n=2 \left(−\dfrac{1}{3}\right)^{n−1}.\nonumber \]
Mlolongo\(\{2^n\}\) ambao tulijadiliwa mapema ni mlolongo wa kijiometri, ambapo uwiano wa muda wowote kwa muda uliopita ni\(2\). Kwa ujumla, mlolongo wa kijiometri ni mlolongo wowote wa fomu\(a_n=cr^n\).
Kwa kila moja ya Utaratibu zifuatazo, kupata formula wazi kwa\(n^{\text{th}}\) muda wa mlolongo.
- \(−\dfrac{1}{2},\dfrac{2}{3},−\dfrac{3}{4},\dfrac{4}{5},−\dfrac{5}{6},…\)
- \(\dfrac{3}{4},\dfrac{9}{7},\dfrac{27}{10},\dfrac{81}{13},\dfrac{243}{16},…\).
Suluhisho
Kwanza, kumbuka kuwa mlolongo unabadilisha kutoka hasi hadi chanya. Maneno yasiyo ya kawaida katika mlolongo ni hasi, na hata maneno ni chanya. Kwa hiyo,\(n^{\text{th}}\) neno linajumuisha sababu ya\((−1)^n\). Kisha, fikiria mlolongo wa nambari\({1,2,3,…}\) na mlolongo wa denominators\({2,3,4,…}\). Tunaweza kuona kwamba wote wa utaratibu huu ni utaratibu hesabu. \(n^{\text{th}}\)Neno katika mlolongo wa nambari ni\(n\), na\(n^{\text{th}}\) neno katika mlolongo wa denominators ni\(n+1\). Kwa hiyo, mlolongo unaweza kuelezewa na formula wazi
\[a_n=\dfrac{(−1)^nn}{n+1}. \nonumber \]
b Mlolongo wa nambari\(3,9,27,81,243,…\) ni mlolongo wa kijiometri. Nambari ya\(n^{\text{th}}\) neno ni Mlolongo\(3^n\) wa denominators\(4,7,10,13,16,…\) ni mlolongo wa hesabu. denominator ya\(n^{\text{th}}\) neno ni\(4+3(n−1)=3n+1.\) Kwa hiyo, tunaweza kuelezea mlolongo kwa formula wazi\(a_n=\dfrac{3^n}{3n+1.}\)
Pata formula wazi kwa\(n^{\text{th}}\) muda wa mlolongo\(\left\{\dfrac{1}{5},−\dfrac{1}{7},\dfrac{1}{9},−\dfrac{1}{11},…\right\}.\)
- Kidokezo
-
Denominators huunda mlolongo wa hesabu.
- Jibu
-
\(a_n=\dfrac{(−1)^{n+1}}{3+2n}\)
Kwa kila moja ya yafuatayo Utaratibu recursively defined, kupata formula wazi kwa mlolongo.
- \(a_1=2, a_n=−3a_{n−1}\)kwa\(n≥2\)
- \(a_1=\left(\dfrac{1}{2}\right), a_n=a_{n−1}+\left(\dfrac{1}{2}\right)^n\)kwa\(n≥2\)
Suluhisho
a Kuandika maneno machache ya kwanza, tuna
\[ \begin{align*} a_1 &=2 \\[4pt] a_2 &=−3a_1=−3(2)\\[4pt] a_3 &=−3a_2=(−3)^22\\[4pt] a_4 &=−3a_3=(−3)^32.\end{align*}\]
Kwa ujumla,
\(a_n=2(−3)^{n−1}.\)
b Andika maneno machache ya kwanza:
\(a_1=\dfrac{1}{2}\)
\(a_2=a_1+\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}\)
\(a_3=a_2+\left(\dfrac{1}{2}\right)^3=\dfrac{3}{4}+\dfrac{1}{8}=\dfrac{7}{8}\)
\(a_4=a_3+\left(\dfrac{1}{2}\right)^4=\dfrac{7}{8}+\dfrac{1}{16}=\dfrac{15}{16}\).
Kutoka kwa mfano huu, tunapata formula wazi
\(a_n=\dfrac{2^n−1}{2^n}=1−\dfrac{1}{2^n}\).
Kupata formula wazi kwa mlolongo defined recursively vile kwamba\(a_1=−4\) na\(a_n=a_{n−1}+6\).
- Kidokezo
-
Hii ni mlolongo wa hesabu.
- Jibu
-
\(a_n=6n−10\)
Kikomo cha Mlolongo
Swali la msingi linalojitokeza kuhusu Utaratibu usio ni tabia ya maneno kama\(n\) anapata kubwa. Kwa kuwa mlolongo ni kazi defined juu ya integers chanya, ni mantiki ya kujadili kikomo ya maneno kama\(n→∞\). Kwa mfano, fikiria zifuatazo Utaratibu nne na tabia zao tofauti kama\(n→∞\) (Kielelezo\(\PageIndex{2}\)):
- \(\{1+3n\}=\{4,7,10,13,…\}.\)maneno\(1+3n\) kuwa kiholela kubwa kama\(n→∞\). Katika kesi hiyo, tunasema kwamba\(1+3n→∞\) kama\(n→∞.\)
- \(\left\{1− \left(\dfrac{1}{2}\right) ^n\right\}=\left\{ \dfrac{1}{2} ,\dfrac{3}{4},\dfrac{7}{8},\dfrac{15}{16}\,…\right\}.\)Masharti\(1−\left(\dfrac{1}{2}\right)^n→1\) kama\(n→∞.\)
- \(\{(−1)^n\}=\{−1,1,−1,1,…\}.\)maneno mbadala lakini si mbinu moja thamani kama\(n→∞.\)
- \(\left\{\dfrac{(−1)^n}{n}\right\}=\left\{−1,\dfrac{1}{2},−\dfrac{1}{3},\dfrac{1}{4},…\right\}.\)maneno mbadala kwa mlolongo huu pia, lakini\(\dfrac{(−1)^n}{n}→0\) kama\(n→∞.\)
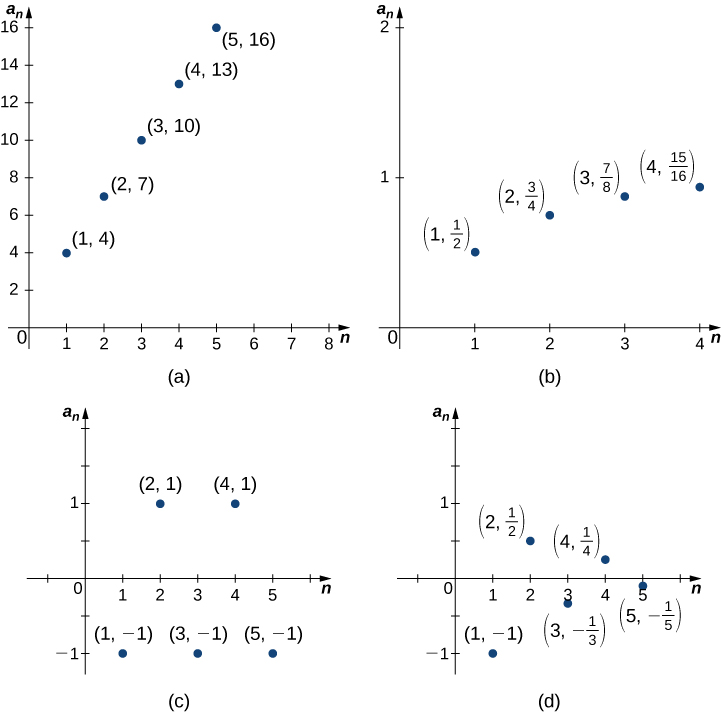
Kutokana na mifano hii, tunaona uwezekano kadhaa kwa ajili ya tabia ya suala la mlolongo kama\(n→∞\). Katika mbili za utaratibu, maneno yanakaribia idadi ya mwisho kama\(n→∞.\) Katika utaratibu mwingine wawili, maneno hayana. Kama suala la mlolongo mbinu idadi ya mwisho\(L\) kama\(n→∞\), tunasema kwamba mlolongo ni convergent mlolongo na idadi halisi L ni kikomo cha mlolongo. Tunaweza kutoa ufafanuzi rasmi hapa.
Kutokana na mlolongo\({a_n},\) kama maneno inaweza kuwa kiholela karibu na idadi ya mwisho\(L\) kama n inakuwa kutosha kubwa, tunasema\(\{a_n\}\) ni mlolongo convergent na\(L\) ni kikomo cha mlolongo. Katika kesi hii, tunaandika
\[\lim_{n→∞}a_n=L. \nonumber \]
Kama mlolongo\(\{a_n\}\) si convergent, tunasema ni mlolongo tofauti.
Kutoka Kielelezo, tunaona kwamba maneno katika mlolongo\(\left\{1− \left(\dfrac{1}{2}\right)^n\right\}\) ni kuwa kiholela karibu na\(1\) kama\(n\) inakuwa kubwa sana. Tunahitimisha kwamba\(\left\{1−\left(\dfrac{1}{2}\right)^n\right\}\) ni mlolongo convergent na kikomo yake ni\(1\). Kwa upande mwingine, kutoka Kielelezo, tunaona kwamba maneno katika mlolongo\(1+3n\) si inakaribia idadi ya mwisho kama\(n\) inakuwa kubwa. Tunasema kwamba\(\{1+3n\}\) ni mlolongo tofauti.
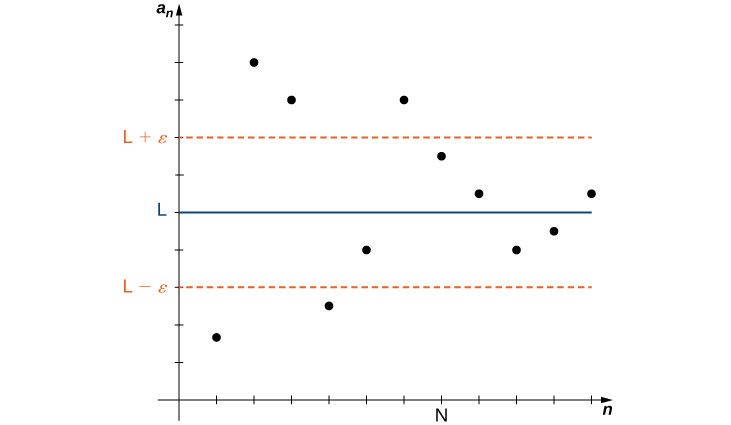
Katika ufafanuzi usio rasmi kwa kikomo cha mlolongo, tulitumia maneno “karibu karibu” na “kutosha kwa kiasi kikubwa.” Ingawa maneno haya husaidia kuonyesha maana ya mlolongo unaobadilika, wao ni kiasi fulani haijulikani. Kuwa sahihi zaidi, sisi sasa sasa ufafanuzi rasmi zaidi ya kikomo kwa mlolongo na kuonyesha mawazo haya graphically katika Kielelezo.
Mlolongo\(\{a_n\}\) hujiunga na idadi halisi\(L\) ikiwa kwa wote\(ε>0\), kuna integer\(N\) kama hiyo kwa wote\(n ≥ N\)\(|a_n−L| < ε\). Nambari\(L\) ni kikomo cha mlolongo na tunaandika
\[\lim_{n→∞}a_n = L \text{ or } a_n→L. \nonumber \]
Katika kesi hii, tunasema mlolongo\(\{a_n\}\) ni mlolongo unaobadilika. Kama mlolongo haina hukutana, ni mlolongo tofauti, na tunasema kikomo haipo.
Sisi remark kwamba muunganiko au tofauti ya mlolongo\(\{a_n\}\) inategemea tu kile kinachotokea kwa maneno\(a_n\) kama\(n→∞\). Kwa hiyo, kama idadi ya mwisho ya maneno\(b_1,b_2,…,b_N\) huwekwa kabla ya\(a_1\) kuunda mlolongo mpya
\[b_1,\,b_2,\,…,\,b_N,\,a_1,\,a_2,\,…,\nonumber \]
mlolongo huu mpya\(\{a_n\}\) zitajiunga kama hujiunga na kupatanisha kama\(\{a_n\}\) diverges. Zaidi ya hayo, kama mlolongo\(\{a_n\}\) hujiunga na\(L\), mlolongo huu mpya pia hujiunga na\(L\).
Kama ilivyoelezwa hapo juu, kama mlolongo haujiunga, inasemekana kuwa mlolongo tofauti. Kwa mfano, Utaratibu\(\{1+3n\}\) na\(\left\{(−1)^n\right\}\) inavyoonekana katika Kielelezo hutofautiana. Hata hivyo, utaratibu tofauti unaweza kutofautiana kwa njia tofauti. mlolongo\(\left\{(−1)^n\right\}\) diverges kwa sababu maneno mbadala kati\(1\) na\(−1\), lakini si mbinu thamani moja kama\(n→∞\). Kwa upande mwingine, mlolongo\(\{1+3n\}\) diverges kwa sababu maneno\(1+3n→∞\) kama\(n→∞\). Tunasema mlolongo\(\{1+3n\}\) hupungua kwa infinity na kuandika\(\displaystyle \lim_{n→∞}(1+3n)=∞\). Ni muhimu kutambua kwamba notation hii haimaanishi kikomo cha mlolongo\(\{1+3n\}\) upo. Mlolongo ni, kwa kweli, tofauti. Kuandika kwamba kikomo ni infinity ni lengo tu kutoa taarifa zaidi kuhusu kwa nini mlolongo ni tofauti. Mlolongo unaweza pia kutofautiana na infinity hasi. Kwa mfano, mlolongo\(\{−5n+2\}\) diverges infinity hasi kwa sababu\(−5n+2→−∞\) kama\(n→−∞\). Tunaandika hii kama\(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Kwa sababu mlolongo ni kazi ambao uwanja ni seti ya integers chanya, tunaweza kutumia mali ya mipaka ya kazi ili kuamua kama mlolongo hujiunga. Kwa mfano, kufikiria mlolongo\(\{a_n\}\) na kazi kuhusiana\(f\) defined juu ya namba zote chanya halisi kama kwamba\(f(n)=a_n\) kwa integers wote\(n≥1\). Kwa kuwa uwanja wa mlolongo ni subset ya uwanja wa\(f\), ikiwa\(\displaystyle \lim_{x→∞}f(x)\) ipo, basi mlolongo hujiunga na ina kikomo sawa. Kwa mfano, fikiria mlolongo\(\left\{\dfrac{1}{n}\right\}\) na kazi inayohusiana\(f(x)=\dfrac{1}{x}\). Kwa kuwa kazi\(f\) defined juu ya namba zote halisi\(x>0\) satisfies\(f(x)=\dfrac{1}{x}→0\) kama\(x→∞\), mlolongo\(\left\{\dfrac{1}{n}\right\}\) lazima kukidhi\(\dfrac{1}{n}→0\) kama\(n→∞.\)
Fikiria mlolongo\(\{a_n\}\) kama huo\(a_n=f(n)\) kwa wote\(n≥1\). Kama kuna idadi halisi\(L\) kama hiyo
\[\lim_{x→∞}f(x)=L, \nonumber \]
kisha\(\{a_n\}\) hujiunga na
\[\lim_{n→∞}a_n=L. \nonumber \]
Tunaweza kutumia theorem hii kutathmini\(\displaystyle \lim_{n→∞}r^n\) kwa\(0≤r≤1\). Kwa mfano, fikiria mlolongo\(\left\{(1/2)^n\right\}\) na kazi inayohusiana na ufafanuzi\(f(x)=(1/2)^x\). Tangu\(\displaystyle \lim_{x→∞}(1/2)^x=0\), tunahitimisha kwamba mlolongo\(\left\{(1/2)^n\right\}\) hujiunga na kikomo chake ni\(0\). Vile vile, kwa idadi yoyote halisi\(r\) kama hiyo\(0≤r<1\)\(\displaystyle \lim_{x→∞}r^x=0\), na kwa hiyo mlolongo\(\left\{r^n\right\}\) hujiunga. Kwa upande mwingine, ikiwa, basi\(r=1\)\(\displaystyle \lim_{x→∞}r^x=1\), na hivyo kikomo cha mlolongo\(\left\{1^n\right\}\) ni\(1\). Kama\(r>1\),\(\displaystyle \lim_{x→∞}r^x=∞\), na kwa hiyo hatuwezi kutumia theorem hii. Hata hivyo, katika kesi hii, kama kazi\(r^x\) kukua bila amefungwa kama\(n→∞\), maneno\(r^n\) katika mlolongo kuwa kiholela kubwa kama\(n→∞\), na sisi kuhitimisha kwamba mlolongo\(\left\{r^n\right\}\) diverges kwa infinity kama\(r>1\).
Sisi muhtasari matokeo haya kuhusu mlolongo wa kijiometri\({r^n}\):
\(r^n→0\)kama\(0<r<1\)
\(r^n→1\)kama\(r=1\)
\(r^n→∞\)kama\(r>1\).
Baadaye katika sehemu hii tunazingatia kesi wakati\(r<0\).
Sasa tunazingatia utaratibu wa ngumu zaidi. Kwa mfano, fikiria mlolongo\(\left\{(2/3)^n+(1/4)^n\right\}.\) maneno katika mlolongo huu ni ngumu zaidi kuliko Utaratibu nyingine tumejadiliwa, lakini kwa bahati kikomo cha mlolongo huu imedhamiria kwa mipaka ya Utaratibu mbili\(\left\{(2/3)^n\right\}\) na\(\left\{(1/4)^n\right\}\). Kama sisi kuelezea katika sheria zifuatazo algebraic kikomo, tangu\(\left\{(2/3)^n\right\}\) na\(\left\{1/4)^n\right\}\) wote wanajiunga na\(0\), mlolongo\(\left\{(2/3)^n+(1/4)^n\right\}\) hujiunga na\(0+0=0\). Kama sisi walikuwa na uwezo wa kutathmini kikomo kuwashirikisha mchanganyiko algebraic ya kazi\(f\) na\(g\) kwa kuangalia mipaka ya\(f\) na\(g\) (angalia Utangulizi wa Mipaka), tuna uwezo wa kutathmini kikomo cha mlolongo ambao maneno ni mchanganyiko algebraic ya\(a_n\) na \(b_n\)kwa kutathmini mipaka ya\(\{a_n\}\) na\(\{b_n\}\).
Kutokana\(\{a_n\}\) na utaratibu\(\{b_n\}\) na nambari yoyote halisi\(c\), ikiwa kuna vipindi\(A\) vilivyopo na\(B\) vile vile\(\displaystyle \lim_{n→∞}b_n=B\), basi\(\displaystyle \lim_{n→∞}a_n=A\)
- \(\displaystyle \lim_{n→∞}c=c\)
- \(\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA\)
- \(\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B\)
- \(\displaystyle \lim_{n→∞}(a_n⋅b_n)=\big(\lim_{n→∞}a_n\big)⋅\big(\lim_{n→∞}b_n\big)=A⋅B\)
- \(\displaystyle \lim_{n→∞}\left(\dfrac{a_n}{b_n}\right)=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}=\dfrac{A}{B}\), zinazotolewa\(B≠0\) na kila\(b_n≠0.\)
Sisi kuthibitisha sehemu iii.
Hebu\(ϵ>0\). Tangu\(\displaystyle \lim_{n→∞}a_n=A\), kuna integer chanya ya mara kwa mara\(N_1\) kama hiyo kwa wote\(n≥N_1\). Tangu\(\displaystyle \lim_{n→∞}b_n=B\), kuna mara kwa mara\(N_2\) kama hiyo\(|b_n−B|<ε/2\) kwa wote\(n≥N_2\). Hebu\(N\) kuwa kubwa zaidi\(N_1\) na\(N_2\). Kwa hiyo, kwa wote\(n≥N\),\(|(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{2}+\dfrac{ε}{2}=ε\).
□
Sheria za kikomo za algebraic zinatuwezesha kutathmini mipaka kwa utaratibu wengi. Kwa mfano, fikiria mlolongo\(a_n={\dfrac{1}{n^2}}\). Kama inavyoonekana hapo awali,\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Vile vile, kwa integer yoyote chanya\(k\), tunaweza kuhitimisha kwamba
\[\lim_{n→∞}\dfrac{1}{n^k}=0. \nonumber \]
Katika mfano unaofuata, tunatumia ukweli huu pamoja na sheria za kikomo ili kutathmini mipaka kwa utaratibu mwingine.
Kwa kila moja ya Utaratibu zifuatazo, kuamua kama au mlolongo converges. Ikiwa inabadilika, pata kikomo chake.
- \(\left\{5−\dfrac{3}{n^2}\right\}\)
- \(\left\{\dfrac{3n^4−7n^2+5}{6−4n^4}\right\}\)
- \(\left\{\dfrac{2^n}{n^2}\right\}\)
- \(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\)
Suluhisho
a. tunajua kwamba\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Kutumia ukweli huu, tunahitimisha kuwa
\(\displaystyle \lim_{n→∞}\dfrac{1}{n^2}=\lim_{n→∞}\dfrac{1}{n}.\lim_{n→∞}\dfrac{1}{n}=0.\)
Kwa hiyo,
\(\displaystyle \lim_{n→∞}\left(5−\dfrac{3}{n^2}\right)=\lim_{n→∞}5−3\lim_{n→∞}\dfrac{1}{n^2}=5−3.0=5.\)
Mlolongo hujiunga na kikomo chake ni 5.
b Kwa factoring\(n^4\) nje ya nambari na denominator na kutumia sheria kikomo hapo juu, tuna
\ [kuanza {align*}\ lim_ {n → Δ}\ dfrac {3n ^ 4—7n ^ 2+5} {6—4n ^ 4} &=\ lim_ {n → Δ}\ dfrac {3}\ dfrac {7} {n ^ 2} +\ dfrac {5} {n ^ 4}} {\ dfrac {6} {n ^ 4} -4}\\ [5pt]
&=\ dfrac {\ lim_ {n → Δ} (3-\ dfrac {7} {n ^ 2} +\ dfrac {5} {n ^ 4})} {\ lim_ {n → Δ} (\ dfrac {6} {n ^ 4}}}\\ [5pt]
&=\ dfrac {\ lim_ {n→ Δ} (3) -\ lim_ {n → Δ}\ dfrac {7} {n ^ 2} +\ lim_ {n → Δ}\ dfrac {5} {n ^ 4}} {\ lim_ {n → Δ}\ dfrac {6} {n ^ 4} -\ lim_ {n → Δ} (4)}\\ [5pt]
&=\ dfrac {\ lim_ {n→ lim_ {n → Δ}\ dfrac {n → 1} {n ^ 2} +5\ lim_ {n → Δ}\ dfrac {1} {n ^ 4}} {6}\ lim_ {n → Δ}\ dfrac {1} {n ^ 4}}} {n ^ 4} {n → Δ} (4)}\\ [5pt]
&=\ dfrac {3,170+50} {600} {600} {600} {600} {600} {600} {600} {600} {6-4} =\ dfrac {3} {4}. \ mwisho {align*}\]
Mlolongo hujiunga na kikomo chake ni\(−3/4\).
c. fikiria kazi kuhusiana\(f(x)=2^x/x^2\) defined juu ya idadi yote halisi\(x>0\). Tangu\(2^x→∞\) na\(x^2→∞\) kama\(x→∞\), tumia utawala wa L'Hôpital na uandike
\ [kuanza {align*}\ lim_ {x→ Δ}\ dfrac {2^x} {x ^ 2} &=\ lim_ {x→ Δ}\ dfrac {2^x\ ln2} {2x} &\ maandishi {Chukua derivatives ya nambari na denominator.}\\ [5pt]
&=\ lim_ {x→ Δ}\ dfrac {2^x (\ ln2) ^2} {2} & &\ maandishi {Chukua derivatives tena.}\\ [5pt]
&=Δ. \ mwisho {align*}\]
Tunahitimisha kwamba mlolongo hupungua.
fikiria kazi\(f(x)=\left(1+\dfrac{4}{x}\right)^x\) defined juu ya idadi yote halisi\(x>0\). Kazi hii ina fomu indeterminate\(1^∞\) kama\(x→∞.\) Hebu
\(\displaystyle y=\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\).
Sasa kuchukua logarithm asili ya pande zote mbili za equation, sisi kupata
\(\displaystyle \ln(y)=\ln\left[\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\right]\).
Kwa kuwa kazi\(f(x)=\ln(x)\) inaendelea kwenye uwanja wake, tunaweza kubadilishana kikomo na logarithm ya asili. Kwa hiyo,
\(\displaystyle \ln(y)=\lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]\).
Kutumia mali ya logarithms, tunaandika
\(\displaystyle \lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)\).
Kwa kuwa upande wa kulia wa equation hii ina fomu indeterminate\(∞⋅0\), kuandika upya kama sehemu ya kutumia utawala wa L'Hôpital. Andika
\(\displaystyle \lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)=\lim_{x→∞}\dfrac{\ln\left(1+4/x\right)}{1/x}\).
Kwa kuwa upande wa kulia ni sasa katika fomu indeterminate 0/0, tunaweza kutumia utawala wa L'Hôpital. Sisi kuhitimisha kwamba
\(\displaystyle \lim_{x→∞}\dfrac{\ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+4/x}=4.\)
Kwa hiyo,\(\ln(y)=4\) na\(y=e^4\). Kwa hiyo, tangu\(\displaystyle \lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x=e^4\), tunaweza kuhitimisha kwamba mlolongo\(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\) hujiunga na\(e^4\).
Fikiria mlolongo\(\left\{(5n^2+1)/e^n\right\}.\) Kuamua kama au mlolongo hujiunga. Ikiwa inabadilika, pata kikomo chake.
- Kidokezo
-
Tumia utawala wa L'Hôpital.
- Jibu
-
Mlolongo hujiunga, na kikomo chake ni\(0\)
Kumbuka kwamba ikiwa\(f\) ni kazi inayoendelea kwa thamani\(L\), basi\(f(x)→f(L)\) kama\(x→L\). Wazo hili linatumika kwa Utaratibu pia. Tuseme mlolongo\(a_n→L\), na kazi\(f\) ni kuendelea katika\(L\). Kisha\(f(a_n)→f(L)\). Mali hii mara nyingi inatuwezesha kupata mipaka kwa utaratibu ngumu. Kwa mfano, fikiria mlolongo\(\sqrt{5−\dfrac{3}{n^2}}\). Kutoka Mfano a. tunajua mlolongo\(5−\dfrac{3}{n^2}→5\). Tangu\(\sqrt{x}\) ni kazi ya kuendelea katika\(x=5\),
\[\lim_{n→∞}\sqrt{5−\dfrac{3}{n^2}}=\sqrt{\lim_{n→∞}(5−\dfrac{3}{n^2})}=\sqrt{5}.\nonumber \]
Fikiria mlolongo\(\{a_n\}\) na tuseme kuna idadi halisi\(L\) kama kwamba mlolongo\(\{a_n\}\) hujiunga na\(L\). Tuseme\(f\) ni kazi ya kuendelea katika\(L\). Kisha kuna integer\(N\) kama kwamba\(f\) ni defined katika maadili yote kwa\(n≥N\), na mlolongo\(\{f(a_n)\}\) hujiunga na\(f(L)\) (Kielelezo\(\PageIndex{4}\)).
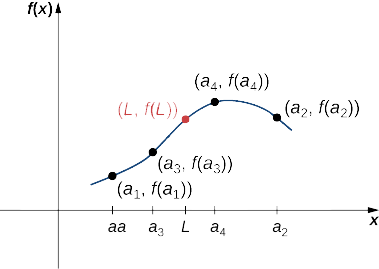
Hebu\(ϵ>0.\) Tangu\(f\) ni kuendelea katika\(L\), kuna\(δ>0\) vile kwamba\(|f(x)−f(L)|<ε\) kama\(|x−L|<δ\). Tangu mlolongo\(\{a_n\}\) hujiunga na\(L\), kuna\(N\) vile kwamba\(|a_n−L|<δ\) kwa ajili ya wote\(n≥N\). Kwa hiyo, kwa wote\(n≥N\)\(|a_n−L|<δ\), ambayo ina maana\(|f(a_n)−f(L)|<ε\). Tunahitimisha kwamba mlolongo\(\{f(a_n)\}\) hujiunga na\(f(L)\).
□
Kuamua kama mlolongo\(\left\{\cos(3/n^2)\right\}\) hujiunga. Ikiwa inabadilika, pata kikomo chake.
Suluhisho:
Kwa kuwa mlolongo\(\left\{3/n^2\right\}\) hujiunga\(0\) na\(\cos x\) kuendelea katika\(x=0\), tunaweza kuhitimisha kwamba mlolongo\(\left\{\cos(3/n^2)\right\}\) hujiunga na
\(\displaystyle \lim_{n→∞}\cos\left(\dfrac{3}{n^2}\right)=\cos 0=1.\)
Kuamua kama mlolongo\(\left\{\sqrt{\dfrac{2n+1}{3n+5}}\right\}\) hujiunga. Ikiwa inabadilika, pata kikomo chake.
- Kidokezo
-
Fikiria mlolongo\(\left\{\dfrac{2n+1}{3n+5}\right\}.\)
- Jibu
-
Mlolongo hujiunga, na kikomo chake ni\(\sqrt{2/3}\).
Theorem nyingine kuwashirikisha mipaka ya Utaratibu ni ugani wa Fanya Theorem kwa mipaka kujadiliwa katika Utangulizi wa Mipaka.
Fikiria Utaratibu\(\{a_n\}, \, \{b_n\},\) na\(\{c_n\}\). Tuseme kuna integer\(N\) kama vile
\(a_n≤b_n≤c_n\)kwa ajili ya wote\(n≥N.\)
Kama kuna idadi halisi\(L\) kama hiyo
\[\lim_{n→∞}a_n=L=\lim_{n→∞}c_n, \nonumber \]
kisha\(\{b_n\}\) hujiunga na\(\displaystyle \lim_{n→∞}b_n=L\) (Kielelezo\(\PageIndex{5}\)).
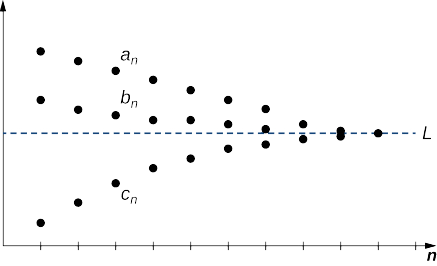
Hebu\(ε>0.\) Tangu mlolongo\(\{a_n\}\) hujiunga na\(L\), kuna integer\(N_1\) vile kwamba\(|a_n−L|<ε\) kwa ajili ya wote\(n≥N_1\). Vile vile, tangu\(\{c_n\}\) hujiunga na\(L\), kuna integer\(N_2\) kama hiyo\(|c_n−L|<ε\) kwa wote\(n≥N_2\). Kwa dhana, kuna integer\(N\) kama hiyo\(a_n≤b_n≤c_n\) kwa wote\(n≥N\). Hebu\(M\) kuwa kubwa zaidi ya\(N_1,\, N_2\), na\(N\). Lazima tuonyeshe kwamba\(|b_n−L|<ε\) kwa wote\(n≥M\). Kwa wote\(n≥M\),
\[−ε<−|a_n−L|≤a_n−L≤b_n−L≤c_n−L≤|c_n−L|<ε\nonumber \]
Kwa hiyo,\(−ε<b_n−L<ε,\) na sisi kuhitimisha kwamba\(|b_n−L|<ε\) kwa wote\(n≥M\), na sisi kuhitimisha kwamba mlolongo\({b_n}\) hujiunga na\(L\).
□
Tumia Theorem itapunguza kupata kikomo cha kila moja ya Utaratibu wafuatayo.
- \(\left\{\dfrac{\cos\, n}{n^2}\right\}\)
- \(\left\{\left(−\dfrac{1}{2}\right)^n\right\}\)
Suluhisho
a Tangu\(−1≤\cos n≤1\) kwa integers wote\(n\), tuna
\(−\dfrac{1}{n^2} ≤ \dfrac{\cos n}{n^2}≤\dfrac{1}{n^2}.\)
Tangu\(−1/n^2→0\) na\(1/n^2→0\), tunahitimisha kuwa\(\cos n/n^2→0\) pia.
b Tangu
\(−\dfrac{1}{2^n} ≤ \left(−\dfrac{1}{2}\right)^n ≤ \dfrac{1}{2^n}\)
kwa integers wote chanya\(n, \, −1/2^n→0\) na\(1/2^n→0,\) tunaweza kuhitimisha kwamba\((−1/2)^n→0.\)
Kupata\(\displaystyle \lim_{n→∞}\dfrac{2n−\sin\, n}{n}.\)
- Kidokezo
-
Tumia ukweli kwamba\(−1≤\sin n≤1.\)
- Jibu
-
\(2\)
Kwa kutumia wazo kutoka Mfano\(\PageIndex{5}\) b tunahitimisha kwamba\(r^n→0\) kwa idadi yoyote halisi r\(−1<r<0.\) kama kwamba\(r<−1\), mlolongo\({r^n}\) diverges kwa sababu maneno oscillate na kuwa kiholela kubwa katika ukubwa. Ikiwa\(r=−1\), mlolongo\({r^n}={(−1)^n}\) hupungua, kama ilivyojadiliwa hapo awali. Hapa ni muhtasari wa mali kwa utaratibu wa kijiometri.
\(r^n→0 \text{ if } |r|<1\)
\(r^n→1\text{ if } r=1\)
\(r^n→∞\text{ if } r>1\)
\(\left\{r^n\right\} \text{ diverges if } r≤−1\)
Utaratibu umepakana
Sasa tunageuka mawazo yetu kwa moja ya theorems muhimu zaidi zinazohusisha utaratibu: Theorem ya Monotone Convergence. Kabla ya kusema theorem, tunahitaji kuanzisha nenosiri na motisha. Tunaanza kwa kufafanua maana gani kwa mlolongo kuwa imepakana.
\(\{a_n\}\)Mlolongo umepakana hapo juu ikiwa kuna idadi halisi\(M\) kama hiyo
\(a_n≤M\)
kwa integers wote chanya\(n\).
\(\{a_n\}\)Mlolongo umepakana chini ikiwa kuna idadi halisi\(m\) kama hiyo
\(m≤a_n\)
kwa integers wote chanya\(n\).
mlolongo\(\{a_n\}\) ni mlolongo imepakana kama imepakana juu na imepakana chini.
Kama mlolongo si imepakana, ni mlolongo unbounded.
Kwa mfano, mlolongo\(\{1/n\}\) umepakana hapo juu kwa sababu\(1/n≤1\) kwa integers zote nzuri\(n\). Pia imepakana chini kwa sababu\(1/n≥0\) kwa integers zote chanya\(n\). Kwa hiyo,\(\{1/n\}\) ni mlolongo imepakana. Kwa upande mwingine, fikiria mlolongo\(\left\{2^n\right\}\). Kwa sababu\(2^n≥2\) kwa wote\(n≥1\), mlolongo umefungwa chini. Hata hivyo, mlolongo haujafungwa hapo juu. Kwa hiyo,\(\left\{2^n\right\}\) ni mlolongo unbounded.
Sasa tunazungumzia uhusiano kati ya mipaka na ushirikiano. Tuseme mlolongo\(\{a_n\}\) ni unbounded. Kisha si imepakana juu, au si imepakana chini, au wote wawili. Katika hali yoyote, kuna maneno ambayo ni kiholela kubwa katika ukubwa kama\(n\) anapata kubwa. Matokeo yake, mlolongo\(\{a_n\}\) hauwezi kugeuka. Kwa hiyo, kuwa imefungwa ni hali muhimu kwa mlolongo wa kugeuka.
Ikiwa mlolongo\(\{a_n\}\) unajiunga, basi umefungwa.
Kumbuka kuwa mlolongo kuwa imepakana si hali ya kutosha kwa mlolongo wa kuungana. Kwa mfano, mlolongo\(\left\{(−1)^n\right\}\) imepakana, lakini mlolongo diverges kwa sababu mlolongo oscillates kati\(1\)\(−1\) na kamwe mbinu idadi ya mwisho. Sasa tunajadili hali ya kutosha (lakini sio lazima) kwa mlolongo uliowekwa ili kugeuza.
Fikiria mlolongo imepakana\(\{a_n\}\). Tuseme mlolongo\(\{a_n\}\) unaongezeka. Hiyo ni,\(a_1≤a_2≤a_3….\) Tangu mlolongo ni kuongezeka, maneno si oscillating. Kwa hiyo, kuna uwezekano wawili. Mlolongo unaweza kutofautiana kwa infinity, au inaweza kugeuka. Hata hivyo, tangu mlolongo umepakana, umepakana hapo juu na mlolongo hauwezi kugeuka kwa infinity. Tunahitimisha kwamba\(\{a_n\}\) hujiunga. Kwa mfano, fikiria mlolongo
\[\left\{\dfrac{1}{2},\,\dfrac{2}{3},\,\dfrac{3}{4},\,\dfrac{4}{5},\,…\right\}. \nonumber \]
Kwa kuwa mlolongo huu unaongezeka na umepakana hapo juu, hujiunga. Kisha, fikiria mlolongo
\[\left\{2,\,0,\,3,\,0,\,4,\,0,\,1,\,−\dfrac{1}{2},\,−\dfrac{1}{3},\,−\dfrac{1}{4},\,…\right\}. \nonumber \]
Hata kama mlolongo si kuongezeka kwa maadili yote ya\(n\), tunaona kwamba\(−1/2<−1/3<−1/4<⋯\). Kwa hiyo, kuanzia na muda wa nane\(a_8=−1/2\), mlolongo unaongezeka. Katika kesi hii, tunasema mlolongo hatimaye kuongezeka. Kwa kuwa mlolongo umefungwa hapo juu, hujiunga. Pia ni kweli kwamba ikiwa mlolongo unapungua (au hatimaye kupungua) na umefungwa chini, pia hujiunga.
Mlolongo\(\{a_n\}\) unaongezeka kwa wote\(n≥n_0\) ikiwa
\(a_n≤a_{n+1}\)kwa ajili ya wote\(n≥n_0\).
Mlolongo\(\{a_n\}\) ni kupungua kwa wote\(n≥n_0\) kama
\(a_n ≥ a_{n+1}\)kwa ajili ya wote\(n≥n_0\).
Mlolongo\(\{a_n\}\) ni mlolongo wa monotone kwa wote\(n≥n_0\) ikiwa unaongezeka kwa wote\(n≥n_0\) au kupungua kwa wote\(n≥n_0\).
Sasa tuna ufafanuzi muhimu ili kutaja Theorem ya Monotone Convergence, ambayo inatoa hali ya kutosha ya kuunganisha mlolongo.
Ikiwa\(\{a_n\}\) ni mlolongo uliopangwa na kuna integer nzuri\(n_0\) kama hiyo\(\{a_n\}\) ni monotone kwa wote\(n≥n_0\), kisha\(\{a_n\}\) hujiunga.
Ushahidi wa theorem hii ni zaidi ya upeo wa maandishi haya. Badala yake, tunatoa grafu ili kuonyesha intuitively kwa nini theorem hii ina maana (Kielelezo\(\PageIndex{6}\)).
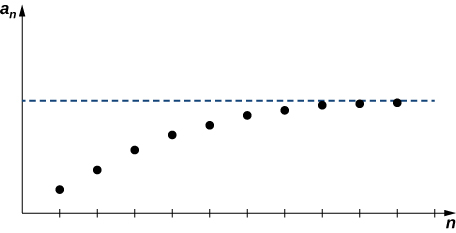
Katika mfano unaofuata, tunaonyesha jinsi Theorem ya Monotone Convergence inaweza kutumika kuthibitisha muunganiko wa mlolongo.
Kwa kila moja ya utaratibu wafuatayo, tumia Theorem ya Monotone Convergence ili kuonyesha mlolongo hujiunga na kupata kikomo chake.
- \(\left\{\dfrac{4^n}{n!}\right\}\)
- \(\{a_n\}\)defined recursively vile kwamba
\(a_1=2\) na\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}\) kwa wote\(n≥2.\)
Suluhisho
a Kuandika maneno machache ya kwanza, tunaona kwamba
\(\left\{\dfrac{4^n}{n!}\right\}=\left\{4,\,8,\,\dfrac{32}{3},\,\dfrac{32}{3},\,\dfrac{128}{15},\,…\right\}.\)
Mara ya kwanza, maneno yanaongezeka. Hata hivyo, baada ya muda wa tatu, maneno yanapungua. Kwa kweli, maneno yanapungua kwa wote\(n≥3\). Tunaweza kuonyesha hii kama ifuatavyo.
\(a_{n+1}=\dfrac{4^{n+1}}{(n+1)!}=\dfrac{4}{n+1}⋅\dfrac{4^n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\)kama\(n≥3.\)
Kwa hiyo, mlolongo unapungua kwa wote\(n≥3\). Zaidi ya hayo, mlolongo umefungwa chini kwa\(0\) sababu\(4n/n!≥0\) kwa integers zote nzuri\(n\). Kwa hiyo, kwa Theorem ya Monotone Convergence, mlolongo hujiunga.
Ili kupata kikomo, tunatumia ukweli kwamba mlolongo hujiunga na kuruhusu\(\displaystyle L=\lim_{n→∞}a_n\). Sasa angalia uchunguzi huu muhimu. Fikiria\(\displaystyle \lim_{n→∞}a_{n+1}\). Tangu
\(\{a_{n+1}\}=\{a_2,\,a_3,\,a_4,\,…\},\)
tofauti tu kati ya Utaratibu\(\{a_{n+1}\}\) na\(\{a_n\}\) ni kwamba\(\{a_{n+1}\}\) omits muda wa kwanza. Kwa kuwa idadi ya mwisho ya maneno haiathiri muunganiko wa mlolongo,
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}a_n=L.\)
Kuchanganya ukweli huu na equation
\(a_{n+1}=\dfrac{4}{n+1}a_n\)
na kuchukua kikomo cha pande zote mbili za equation
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}\dfrac{4}{n+1}a_n\),
tunaweza kuhitimisha kwamba
\(L=0⋅L=0.\)
b Kuandika maneno kadhaa ya kwanza,
\(\left\{2,\,\dfrac{5}{4},\,\dfrac{41}{40},\,\dfrac{3281}{3280},\,…\right\}.\)
tunaweza kudhani kwamba mlolongo ni kupungua na imepakana chini na\(1\). Kuonyesha kwamba mlolongo imepakana chini na\(1\), tunaweza kuonyesha kwamba
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≥1.\)
Ili kuonyesha hili, kwanza uandike tena
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}=\dfrac{a^2_n+1}{2a_n}\).
Tangu\(a_1>0\) na\(a_2\) hufafanuliwa kama jumla ya maneno mazuri,\(a_2>0.\) Vile vile, maneno yote\(a_n>0\). Kwa hiyo,
\(\dfrac{a^2n+1}{2a_n}≥1\)
kama na tu kama
\(a^2_n+1≥2a_n\).
Kuandika kukosekana kwa usawa\(a^2_n+1≥2a_n\) kama\(a^2_n−2a_n+1≥0\), na kwa kutumia ukweli kwamba
\(a^2_n−2a_n+1=(a_n−1)^2≥0\)
kwa sababu mraba wa idadi yoyote halisi ni nonnegative, tunaweza kuhitimisha kwamba
\(\dfrac{a^n}{2}+\dfrac{1}{2a_n}≥1.\)
Ili kuonyesha kwamba mlolongo unapungua, lazima tuonyeshe kwamba\(a_{n+1}≤a_n\) kwa wote\(n≥1\). Tangu\(1≤a^2_n\), inafuata kwamba
\(a^2_n+1≤2a^2_n\).
Kugawanya pande zote mbili na\(2a_n\), sisi kupata
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.\)
Kutumia ufafanuzi wa\(a_{n+1}\), tunahitimisha kwamba
\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n\).
Tangu\(\{a_n\}\) imepakana chini na kupungua, na Theorem ya Monotone Convergence, inabadilika.
Ili kupata kikomo, basi\(\displaystyle L=\lim_{n→∞}a_n\). Kisha kwa kutumia uhusiano upprepning na ukweli kwamba\(\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}\), tuna
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}(\dfrac{a_n}{2}+\dfrac{1}{2a_n})\),
na kwa hiyo
\(L=\dfrac{L}{2}+\dfrac{1}{2L}\).
Kuzidisha pande zote mbili za equation hii na\(2L\), sisi kufika katika equation
\(2L^2=L^2+1\).
Kutatua equation hii kwa\(L,\) sisi kuhitimisha kwamba\(L^2=1\), ambayo ina maana\(L=±1\). Kwa kuwa maneno yote ni chanya, kikomo\(L=1\).
Fikiria mlolongo\(\{a_n\}\) defined recursively vile kwamba\(a_1=1\),\(a_n=a_{n−1}/2\). Tumia Theorem ya Monotone Convergence kuonyesha kwamba mlolongo huu hujiunga na kupata kikomo chake.
- Kidokezo
-
Onyesha mlolongo unapungua na umefungwa chini.
- Jibu
-
\(0\).
namba Fibonacci hufafanuliwa recursively na mlolongo\(\left\{F_n\right\}\) ambapo\(F_0=0, \, F_1=1\) na kwa\(n≥2,\)
\(F_n=F_{n−1}+F_{n−2}.\)
Hapa tunaangalia mali ya namba za Fibonacci.
1. Andika namba ishirini za kwanza za Fibonacci.
2. Pata fomu iliyofungwa kwa mlolongo wa Fibonacci kwa kutumia hatua zifuatazo.
Fikiria mlolongo recursively defined\({x_n}\) wapi\(x_0=c\) na\(x_{n+1}=ax_n\). Onyesha kwamba mlolongo huu unaweza kuelezewa na formula iliyofungwa\(x_n=ca^n\) kwa wote\(n≥0.\)
b Kutumia matokeo kutoka kwa sehemua. kama motisha, tafuta suluhisho la equation
\(F_n=F_{n−1}+F_{n−2}\)
ya fomu\(F_n=cλ^n\). Kuamua nini maadili mawili kwa\(λ\) itaruhusu\(F_n\) kukidhi equation hii.
Fikiria ufumbuzi mbili kutoka sehemu b.:\(λ_1\) na\(λ_2\). Hebu\(F_n=c_1λ_1^n+c_2λ_2^n\). Tumia hali ya awali\(F_0\) na\(F_1\) kuamua maadili kwa mara kwa mara\(c_1\)\(c_2\) na uandike fomu iliyofungwa\(F_n\).
3. Tumia jibu katika 2 c. ili kuonyesha kwamba
\[\lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\nonumber \]
Nambari\(ϕ=(1+\sqrt{5})/2\) inajulikana kama uwiano wa dhahabu (Kielelezo na Kielelezo).


Dhana muhimu
- Kuamua kuunganishwa kwa mlolongo uliotolewa na formula wazi\(a_n=f(n)\), tunatumia mali ya mipaka ya kazi.
- Kama\(\{a_n\}\) na\(\{b_n\}\) ni convergent Utaratibu kwamba hujiunga\(A\) na na\(B,\) kwa mtiririko huo, na\(c\) ni idadi yoyote halisi, basi mlolongo\(\{ca_n\} \) hujiunga\(c\cdot A,\) na Utaratibu\(\{a_n±b_n\}\) hujiunga na mlolongo\(\{a_n\cdot b_n\}\) hujiunga\(A⋅B,\) na\(A±B,\) mlolongo\(\{a_n/b_n\}\) hujiunga na\(A/B,\) zinazotolewa\(B≠0.\)
- Ikiwa mlolongo umepakana na monotone, basi hujiunga, lakini sio utaratibu wote unaobadilika ni monotone.
- Kama mlolongo ni unbounded, ni diverges, lakini si wote Utaratibu tofauti ni unbounded.
- Mlolongo wa kijiometri\(\left\{r^n\right\}\) hujiunga ikiwa na tu ikiwa\(|r|<1\) au\(r=1\).
faharasa
- mlolongo wa hesabu
- mlolongo ambao tofauti kati ya kila jozi ya maneno mfululizo ni sawa inaitwa mlolongo wa hesabu
- imefungwa hapo juu
- mlolongo\(\{a_n\}\) umepakana hapo juu ikiwa kuna mara kwa mara\(M\) kama vile\(a_n≤M\) kwa integers zote nzuri\(n\)
- imepakana chini
- mlolongo\(\{a_n\}\) umefungwa chini ikiwa kuna mara kwa mara\(M\) kama vile\(M≤a_n\) kwa integers zote nzuri\(n\)
- imepakana mlolongo
- mlolongo\(\{a_n\}\) umepakana ikiwa kuna mara kwa mara\(M\) kama vile\(|a_n|≤M\) kwa integers zote nzuri\(n\)
- mlolongo wa kuungana
- mlolongo unaojitokeza ni mlolongo\(\{a_n\}\) ambao kuna idadi halisi\(L\) kama hiyo ambayo\(a_n\) ni karibu na kwa muda mrefu\(L\) kama\(n\) ni kubwa ya kutosha
- mlolongo tofauti
- mlolongo ambao haujajibadilisha ni tofauti
- formula wazi
- mlolongo inaweza kuelezwa na formula wazi kama kwamba\(a_n=f(n)\)
- mlolongo jiometri
- mlolongo\(\{a_n\}\) ambao uwiano\(a_{n+1}/a_n\) ni sawa kwa integers zote nzuri\(n\) huitwa mlolongo wa kijiometri
- index kutofautiana
- subscript kutumika kufafanua maneno katika mlolongo inaitwa index
- kikomo cha mlolongo
- idadi\(L\) halisi ambayo mlolongo hujiunga inaitwa kikomo cha mlolongo
- monotone mlolongo
- mlolongo unaoongezeka au kupungua
- uhusiano wa kurudia
- uhusiano wa kurudia ni uhusiano ambao neno\(a_n\) katika mlolongo hufafanuliwa kwa suala la maneno ya awali katika mlolongo
- mlolongo
- orodha iliyoamriwa ya idadi ya fomu\(a_1,\,a_2,\,a_3,\,…\) ni mlolongo
- muda
- nambari\(a_n\) katika mlolongo\(\{a_n\}\) inaitwa\(n^{\text{th}}\) muda wa mlolongo
- mlolongo usio na mipaka
- mlolongo ambao haujafungwa unaitwa unbounded


