Skip to main content
Global

9.0: Utangulizi wa Mlolongo na Mfululizo

  1. Last updated
  2. Save as PDF
  • Page ID
    178877

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Snowflake ya Koch imejengwa kutoka kwa idadi isiyo na kipimo ya pembetatu zisizo za kuingiliana. Kwa hiyo, tunaweza kueleza eneo lake kama jumla ya maneno mengi sana. Tunaongezaje idadi isiyo na kipimo ya maneno? Je, jumla ya idadi isiyo na kipimo ya maneno inaweza kuwa ya mwisho? Ili kujibu maswali haya, tunahitaji kuanzisha dhana ya mfululizo usio na mwisho, jumla yenye maneno mengi sana. Baada ya kufafanua zana muhimu, tutaweza kuhesabu eneo la theluji la Koch.

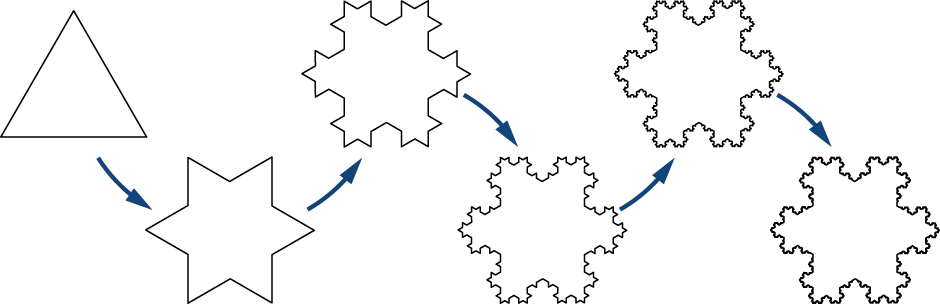
    Hii ni mchoro wa iterations kadhaa ya theluji ya Koch, ambayo imeundwa kupitia mchakato wa kuingiliana. Kesi ya kwanza ni pembetatu ya equilateral. Mara tano, sehemu ya tatu ya katikati ya kila sehemu ya mstari inabadilishwa na pembetatu ya equilateral inayoelezea nje.
    Kielelezo\(\PageIndex{1}\): Snowflake ya Koch inajengwa kwa kutumia mchakato wa iterative. Kuanzia na pembetatu ya equilateral, kila hatua ya mchakato wa tatu katikati ya kila sehemu ya mstari huondolewa na kubadilishwa na pembetatu ya equilateral inayoelezea nje.

    Mada ya mfululizo usio na kipimo inaweza kuonekana isiyohusiana na calculus tofauti na muhimu. Kwa kweli, mfululizo usio na mwisho ambao maneno yanahusisha nguvu za kutofautiana ni chombo chenye nguvu ambacho tunaweza kutumia ili kueleza kazi kama “polynomials isiyo na kipimo.” Tunaweza kutumia mfululizo usio kutathmini kazi ngumu, takriban integrals uhakika, na kujenga kazi mpya. Aidha, mfululizo usio na mwisho hutumiwa kutatua equations tofauti ambazo zinaonyesha tabia ya kimwili, kutoka kwenye nyaya ndogo za elektroniki hadi satelaiti za Dunia-zinazozunguka.