9.2E: Mazoezi ya Sehemu ya 9.2

Last updated
Save as PDF

Page ID: 178884

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 4, tumia alama ya sigma kuandika kila maneno kama mfululizo usio na kipimo.

1)$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯$

Jibu: $\displaystyle \sum_{n=1}^∞\frac{1}{n}$

2)$ 1−1+1−1+⋯$

3)$ 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...$

Jibu: $\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}$

4)$ \sin 1+\sin \frac{1}{2}+\sin \frac{1}{3}+\sin \frac{1}{4}+⋯$

Katika mazoezi 5 - 8, compute kwanza nne sehemu kiasi$ S_1,…,S_4$ kwa mfululizo kuwa$ n^{\text{th}}$ mrefu$ a_n$ kuanzia na$ n=1$ kama ifuatavyo.

5)$ a_n=n$

Jibu: $ 1,3,6,10$

6)$ a_n=1/n$

7)$ a_n=\sin \frac{nπ}{2}$

Jibu: $ 1,1,0,0$

8)$ a_n=(−1)^n$

Katika mazoezi 9 - 12, compute muda wa jumla$ a_n$ wa mfululizo na jumla ya sehemu iliyotolewa$ S_n$. Ikiwa mlolongo wa kiasi cha sehemu hujiunga, pata kikomo chake$ S$.

9)$ S_n=1−\frac{1}{n}, \quad n≥2$

Jibu: $ a_n=S_n−S_{n−1}=\dfrac{1}{n−1}−\dfrac{1}{n}.$Tangu$\displaystyle S = \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left(1−\frac{1}{n}\right) = 1,$ mfululizo hujiunga$ S=1.$

10)$ S_n=\dfrac{n(n+1)}{2}, \quad n≥1$

11)$ S_n=\sqrt{n},\quad n≥2$

Jibu: $ a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\dfrac{1}{\sqrt{n−1}+\sqrt{n}}.$
Mfululizo hutofautiana kwa sababu kiasi cha sehemu hazipatikani.
Hiyo ni,$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \sqrt{n} = \infty.$

12)$ S_n=2−\dfrac{n+2}{2^n},\quad n≥1$

Kwa kila mfululizo katika mazoezi 13 - 16, tumia mlolongo wa kiasi cha sehemu ili ueleze kama mfululizo unajiunga au hupungua.

13)$\displaystyle \sum_{n=1}^∞\frac{n}{n+2}$

Jibu: $ S_1=1/3,$
$ S_2=1/3+2/4>1/3+1/3=2/3,$
$S_3=1/3+2/4+3/5>3⋅(1/3)=1.$
Kwa ujumla$ S_k>k/3,$ hivyo mfululizo hupungua.
Kumbuka kuwa Mtihani wa$n^{\text{th}}$ Muda wa Divergence pia unaweza kutumika kuthibitisha kwamba mfululizo huu unatofautiana.

14)$\displaystyle \sum_{n=1}^∞(1−(−1)^n))$

15)$\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}$$\quad\Big($ Dokezo: Tumia utengano wa sehemu ya sehemu kama hiyo$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\Big)$

Jibu

$ S_1=1/(2\cdot 3)=1/6=2/3−1/2,$

$ S_2=1/(2\cdot 3)+1/(3\cdot 4)=2/12+1/12=1/4=3/4−1/2,$

$ S_3=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)=10/60+5/60+3/60=3/10=4/5−1/2,$

$ S_4=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)+1/(5\cdot 6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.$

mfano ni$ S_k=\dfrac{k+1}{k+2}−\dfrac{1}{2}.$
Kisha$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left( \dfrac{k+1}{k+2}−\dfrac{1}{2} \right) = \dfrac{1}{2},$ hivyo mfululizo hujiunga$ 1/2.$

16)$\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}$$\quad\Big($ Hint: Fuata hoja$\displaystyle \sum_{n=1}^∞\frac{1}{n}.\Big)$

Tuseme kwamba$\displaystyle \sum_{n=1}^∞a_n=1$, kwamba$\displaystyle \sum_{n=1}^∞b_n=−1$, kwamba$ a_1=2$, na$ b_1=−3$. Tumia habari hii ili kupata jumla ya mfululizo ulioonyeshwa katika mazoezi 17 - 20.

17)$\displaystyle \sum_{n=1}^∞(a_n+b_n)$

Jibu: $ \displaystyle \sum_{n=1}^∞(a_n+b_n) \quad = \quad \sum_{n=1}^∞ a_n + \sum_{n=1}^∞ b_n \quad = \quad 1 + (-1) \quad = \quad 0$

18)$\displaystyle \sum_{n=1}^∞(a_n−2b_n)$

19)$\displaystyle \sum_{n=2}^∞(a_n−b_n)$

Jibu: $\displaystyle \sum_{n=2}^∞(a_n−b_n) \quad = \quad \sum_{n=2}^∞ a_n - \sum_{n=2}^∞ b_n \quad = \quad \left(\sum_{n=1}^∞ a_n - a_1\right) - \left(\sum_{n=1}^∞ b_n -b_1\right) \quad = \quad (1 - 2) - (-1 - (-3)) = -1 - 2 \quad = \quad -3$

20)$\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})$

Katika mazoezi 21 - 26, sema kama mfululizo uliopewa unajiunga au hutofautiana na kuelezea kwa nini.

21)$\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}$ (Kidokezo: Andika upya kwa kutumia mabadiliko ya index.)

Jibu: Mfululizo hutofautiana,$\displaystyle \sum_{n=1001}^∞\frac{1}{n}$

22)$\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}$ (Dokezo: Andika upya kwa kutumia mabadiliko ya index.)

23)$ 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯$

Jibu: Hii ni mfululizo wa kijiometri unaobadilika, tangu$ r=\frac{1}{10}<1$

24)$ 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯$

25)$ 1+\frac{π}{e^2}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯$

Jibu: Hii ni mfululizo wa kijiometri unaobadilika, tangu$ r=π/e^2<1$

26)$ 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯$

Kwa kila mmoja$ a_n$ katika mazoezi 27 - 30, andika jumla yake kama mfululizo wa kijiometri wa fomu$\displaystyle \sum_{n=1}^∞ar^n$. Eleza kama mfululizo unajiunga na ikiwa unafanya, pata thamani halisi ya jumla yake.

27)$ a_1=−1$ na$ \dfrac{a_n}{a_{n+1}}=−5$ kwa$ n≥1.$

Jibu: $\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n$, hujiunga na$ −5/6$

28)$ a_1=2$ na$ \dfrac{a_n}{a_{n+1}}=1/2$ kwa$ n≥1.$

29)$ a_1=10$ na$ \dfrac{a_n}{a_{n+1}}=10$ kwa$ n≥1$.

Jibu: $\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,$hujiunga kwa$\frac{100}{9}$

30)$ a_1=\frac{1}{10}$ na$ a_n/a_{n+1}=−10$ kwa$ n≥1$.

Katika mazoezi 31 - 34, tumia utambulisho$\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n$ (ambayo ni kweli kwa$|y| < 1$) kuelezea kila kazi kama mfululizo wa kijiometri katika muda ulioonyeshwa.

31)$ \dfrac{x}{1+x}$ katika$ x$

Jibu: $\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n$

32)$ \dfrac{\sqrt{x}}{1−x^{3/2}}$ katika$ \sqrt{x}$

33)$ \dfrac{1}{1+\sin^2x}$ katika$\sin x$

Jibu: $\displaystyle \sum_{n=0}^∞(−1)^n\sin^{2n}(x)$

34)$ \sec^2 x$ katika$\sin x$

Katika mazoezi 35 - 38, tathmini mfululizo wa telescoping au hali kama mfululizo unatofautiana.

35)$\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}$

Jibu: $ S_k=2−2^{1/(k+1)}→1$kama$ k→∞.$

36)$\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}$

37)$\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})$

Jibu: $ S_k=1−\sqrt{k+1}$hutengana

38)$\displaystyle \sum_{n=1}^∞(\sin n−\sin(n+1))$

Eleza kila mfululizo katika mazoezi 39 - 42 kama jumla ya darubini na kutathmini jumla yake ya$n^{\text{th}}$ sehemu.

39)$\displaystyle \sum_{n=1}^∞\ln\left(\frac{n}{n+1}\right)$

Jibu: $\displaystyle \sum_{n=1}^∞[\ln n−\ln(n+1)],$
$S_k=−\ln(k+1)$

40)$\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}$ (Dokezo: Factor denominator na kutumia sehemu ndogo.)

41)$\displaystyle \sum_{n=2}^∞\frac{\ln\left(1+\frac{1}{n}\right)}{(\ln n)\ln(n+1)}$

Jibu: $ a_n=\frac{1}{\ln n}−\frac{1}{\ln(n+1)}$na$ S_k=\frac{1}{\ln(2)}−\frac{1}{\ln(k+1)}→\frac{1}{\ln(2)}$

42)$\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}$ (kidokezo: Angalia$ 1/(n2^n)$.

Mfululizo wa jumla wa darubini ni moja ambayo yote lakini maneno machache ya kwanza hughairi baada ya kuhesabu idadi fulani ya maneno mfululizo.

43) Hebu$ a_n=f(n)−2f(n+1)+f(n+2),$ katika ambayo$ f(n)→0$ kama$ n→∞.$ Kupata$\displaystyle \sum_{n=1}^∞a_n$.

Jibu: $\displaystyle \sum_{n=1}^∞a_n=f(1)−f(2)$

44)$ a_n=f(n)−f(n+1)−f(n+2)+f(n+3),$ ambayo$ f(n)→0$ kama$ n→∞$. Kupata$\displaystyle \sum_{n=1}^∞a_n$.

45) Tuseme kwamba$ a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),$ ambapo$ f(n)→0$ kama$ n→∞$. Kupata hali ya coefficients$ c_0,…,c_4$ kwamba kufanya hii jumla telescoping mfululizo.

Jibu: $ c_0+c_1+c_2+c_3+c_4=0$

46) Tathmini$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}$ (kidokezo:$\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)}$)

47) Tathmini$\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.$

Jibu: $\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1},$
$S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2$

48) Kupata formula kwa ajili ya$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+N)}$$ N$ wapi integer chanya.

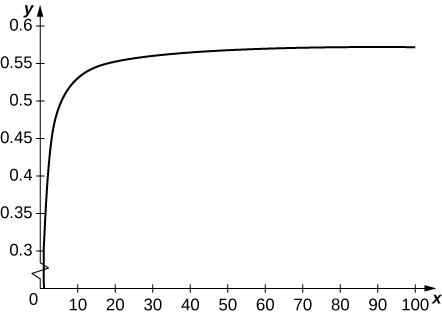
49) [T] Kufafanua mlolongo$\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−\ln k$. Matumizi grafu ya$ 1/x$ kuthibitisha kwamba$ t_k$ ni kuongezeka. Plot$ t_k$ kwa$ k=1…100$ na kusema kama inaonekana kwamba mlolongo hujiunga.

Jibu

$ t_k$converges kwa$ 0.57721…t_k$ ni jumla ya rectangles ya urefu$ 1/k$ juu ya muda$ [k,k+1]$ ambayo uongo juu ya grafu ya$ 1/x$.

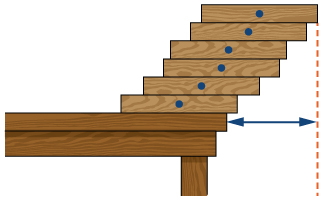
50) [T] Tuseme kwamba vitalu$ N$ sawa vya mstatili vya mstatili vimewekwa moja juu ya nyingine, kuruhusu kwa overhang. Sheria ya Archimedes ya lever inamaanisha kuwa stack ya$ N$ vitalu imara kwa muda mrefu kama katikati ya wingi wa$ (N−1)$ vitalu vya juu iko kwenye makali ya kuzuia chini. Hebu$ x$ kuashiria nafasi ya makali ya kuzuia chini, na fikiria nafasi yake kama kuhusiana na katikati ya kuzuia karibu na chini. Hii ina maana kwamba$ (N−1)x=\left(\frac{1}{2}−x\right)$ au$ x=1/(2N)$. Tumia maneno haya kukokotoa overhang upeo (nafasi ya makali ya kuzuia juu juu ya makali ya kuzuia chini.) Angalia takwimu ifuatayo.

Kila moja ya mfululizo zifuatazo usio hujiunga na nyingi kupewa ya$ π$ au$ 1/π$.

Katika kila kesi, tafuta thamani ya chini ya$ N$ kiasi kwamba jumla ya$ Nth$ sehemu ya mfululizo inakaribia kwa usahihi upande wa kushoto kwa idadi iliyotolewa ya maeneo ya decimal, na kutoa thamani ya takriban. Hadi$ 15$ decimals mahali,$ π=3.141592653589793....$

51) [T]$\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},$ kosa$ <0.0001$

Jibu: $N=22,$
$S_N=6.1415$

52) [T]$\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},$ kosa$ <10^{−4}$

53) [T]$\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},$ kosa$ <10^{−12}$

Jibu: $ N=3,$
$S_N=1.559877597243667...$

54) [T]$\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}$, kosa$ <10^{−15}$

55) [T] sarafu ya haki ni moja ambayo ina uwezekano$ 1/2$ wa kuja juu vichwa wakati flipped.

a. ni uwezekano kwamba sarafu haki kuja mikia$ n$ mara mfululizo?

b. kupata uwezekano kwamba sarafu anakuja vichwa kwa mara ya kwanza baada ya hata idadi ya sarafu flips.

Jibu: a. uwezekano wa yoyote iliyotolewa awali mlolongo wa matokeo kwa$ n$ sarafu flips ni$ 1/2^n$.
b. uwezekano wa kuja juu vichwa kwa mara ya kwanza juu ya$ n$ th flip ni uwezekano wa mlolongo$ TT…TH$ ambayo ni$ 1/2^n$. Uwezekano wa kuja vichwa kwa mara ya kwanza kwenye hata flip ni$\displaystyle \sum_{n=1}^∞1/2^{2n}$ au$ 1/3$.

56) [T] Kupata uwezekano kwamba sarafu haki ni flipped nyingi ya mara tatu kabla ya kuja juu vichwa.

57) [T] Kupata uwezekano kwamba sarafu haki atakuja vichwa kwa mara ya pili baada hata idadi ya flips.

Jibu: $5/9$

58) [T] Kupata mfululizo inayoonyesha uwezekano kwamba sarafu haki atakuja vichwa kwa mara ya pili juu ya nyingi ya flips tatu.

59) [T] inatarajiwa idadi ya mara sarafu haki kuja vichwa hufafanuliwa kama jumla zaidi$ n=1,2,…$ ya$ n$ mara uwezekano kwamba sarafu kuja vichwa hasa$ n$ mara mfululizo, au$ \dfrac{n}{2^{n+1}}$. Compute idadi inatarajiwa ya nyakati mfululizo kwamba sarafu ya haki atakuja vichwa.

Jibu: $\displaystyle E=\sum_{n=1}^∞\frac{n}{2^{n+1}}=1,$kama inaweza kuonyeshwa kwa kutumia summation kwa sehemu

60) [T] mtu amana$ $10$ katika mwanzo wa kila robo katika akaunti ya benki kwamba chuma riba ya kila$ 4%$ mwaka imezungukwa robo mwaka (mara nne kwa mwaka).

Onyesha kuwa maslahi ya kusanyiko baada ya$ n$ robo ni$ $10(\frac{1.01^{n+1}−1}{0.01}−n).$

pata masharti nane ya kwanza ya mlolongo.

c Ni kiasi gani cha riba kilichokusanywa baada ya$ 2$ miaka?

61) [T] Tuseme kwamba kiasi cha madawa ya kulevya katika mfumo wa mgonjwa hupungua kwa sababu ya kuzidisha$ r<1$ kila saa. Tuseme kwamba dozi mpya inasimamiwa kila$ N$ masaa. Pata maelezo ambayo hutoa kiasi$ A(n)$ katika mfumo wa mgonjwa baada ya$ n$ masaa kwa kila mmoja$ n$ kwa suala la kipimo$ d$ na uwiano$ r$. (Kidokezo: Andika$ n=mN+k$, wapi$ 0≤k<N$, na jumla juu ya maadili kutoka kwa vipimo tofauti vinavyotumiwa.)

Jibu: Sehemu ya dozi ya kwanza baada ya$ n$ masaa ni$ dr^n$, sehemu ya dozi ya pili ni$ dr^{n−N}$, na, kwa ujumla, sehemu iliyobaki ya$ m^{\text{th}}$ dozi ni$ dr^{n−mN}$, hivyo$\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},\;\text{where}\,n=k+mN.$

62) [T] Dawa fulani ni bora kwa mgonjwa wastani tu ikiwa kuna angalau$ 1$ mg kwa kilo katika mfumo wa mgonjwa, wakati ni salama tu ikiwa kuna$ 2$ mg zaidi kwa kilo katika mfumo wa mgonjwa wa wastani. Tuseme kwamba kiasi katika mfumo wa mgonjwa hupungua kwa sababu ya kuzidisha ya$ 0.9$ kila saa baada ya dozi inasimamiwa. Kupata muda upeo$ N$ wa masaa kati ya dozi, na sambamba dozi mbalimbali$ d$ (katika mg/kg) kwa ajili ya hii$ N$ ambayo itawezesha matumizi ya madawa ya kulevya kuwa wote salama na ufanisi katika muda mrefu.

63) Tuseme kwamba$ a_n≥0$ ni mlolongo wa idadi. Eleza kwa nini mlolongo wa kiasi sehemu ya$ a_n$ ni kuongezeka.

Jibu: $ S_{N+1}=a_{N+1}+S_N≥S_N$

64) [T] Tuseme kwamba$ a_n$ ni mlolongo wa idadi chanya na mlolongo$ S_n$ wa kiasi sehemu ya$ a_n$ imepakana juu. Eleza kwa nini$\displaystyle \sum_{n=1}^∞a_n$ hujiunga. Je, hitimisho linabakia kweli ikiwa tunaondoa hypothesis$ a_n≥0$?

65) [T] Tuseme kwamba$ a_1=S_1=1$ na kwamba, kwa idadi fulani$ S>1$ na$ 0<k<1$, moja amefafanua$ a_{n+1}=k(S−S_n)$ na$ S_{n+1}=a_{n+1}+S_n$. Je,$ S_n$ hujiunga? Ikiwa ndivyo, kwa nini? (Kidokezo: Kwanza wanasema kuwa$ S_n<S$ kwa wote$ n$ na$ S_n$ inaongezeka.)

Jibu: Tangu$ S>1, a_2>0,$ na tangu$ k<1, S_2=1+a_2<1+(S−1)=S$. Ikiwa$ S_n>S$ kwa baadhi$ n$, basi kuna ndogo zaidi$ n$. Kwa hili$ n, S>S_{n−1}$, hivyo$ S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S$, utata. Hivyo$ S_n<S$ na$ a_{n+1}>0$ kwa ajili ya wote$ n$, hivyo$ S_n$ ni kuongezeka na imepakana na$ S$. Hebu$\displaystyle S_∗=\lim S_n$. Kama$ S_∗<S$, basi$ δ=k(S−S_∗)>0$, lakini tunaweza kupata katika vile kwamba$ S_∗−S_n<δ/2$, ambayo ina maana kwamba$ S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2$, kinyume na kwamba Sun ni kuongezeka kwa$ S_∗$. Hivyo$ S_n→S.$

66) [T] Toleo la ukuaji wa von Bertalanffy linaweza kutumika kukadiria umri wa mtu binafsi katika spishi zinazofanana na urefu wake ikiwa ongezeko la kila mwaka katika mwaka$ n+1$ linatimiza$ a_{n+1}=k(S−S_n)$, na$ S_n$ kama urefu wa mwaka$ n, S$ kama urefu wa kikwazo, na$ k$ kama jamaa ukuaji wa mara kwa mara. Kama$ S_1=3, S=9,$ na$ k=1/2,$ numerically makisio thamani ndogo ya n kama kwamba$ S_n≥8$. Kumbuka kuwa$ S_{n+1}=S_n+a_{n+1}.$ Kupata sambamba$ n$ wakati$ k=1/4.$

67) [T] Tuseme kwamba$\displaystyle \sum_{n=1}^∞a_n$ ni convergent mfululizo wa maneno chanya. Eleza kwa nini$\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.$

Jibu: Hebu$\displaystyle S_k=\sum_{n=1}^ka_n$ na$ S_k→L$. Kisha$ S_k$ hatimaye inakuwa kiholela karibu na$ L$, ambayo ina maana kwamba$\displaystyle L−S_N=\sum_{n=N+1}^∞a_n$ inakuwa kiholela ndogo kama$ N→∞.$

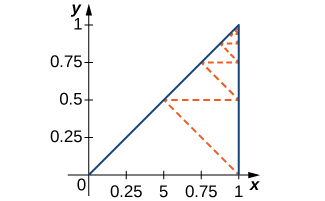
68) [T] Kupata urefu wa dashed Zig-zag njia katika takwimu zifuatazo.

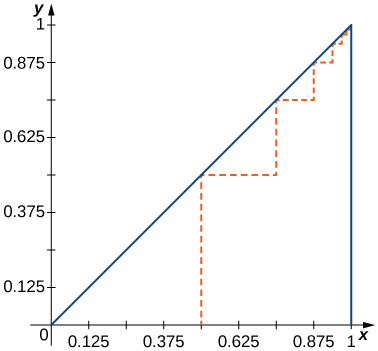
69) [T] Pata urefu wa jumla wa njia iliyopigwa katika takwimu ifuatayo.

Jibu: $\displaystyle L=\left(1+\frac{1}{2}\right)\sum_{n=1}^∞\frac{1}{2^n}=\frac{3}{2}$.

70) [T] Pembetatu ya Sierpinski inapatikana kutoka pembetatu kwa kufuta katikati ya nne kama ilivyoonyeshwa katika hatua ya kwanza, kwa kufuta nne ya katikati ya pembetatu tatu zilizobaki katika hatua ya pili, na kwa ujumla kufuta katikati ya nne ya pembetatu iliyobaki katika kila hatua mfululizo. Kwa kuzingatia kwamba pembetatu ya awali inavyoonekana kwenye takwimu, pata maeneo ya sehemu zilizobaki za pembetatu ya awali baada ya$ N$ hatua na kupata urefu wa jumla wa pembetatu zote za mipaka baada ya$ N$ hatua.

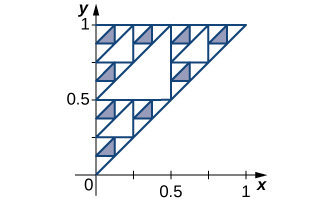
71) [T] Gasket ya Sierpinski inapatikana kwa kugawanya mraba wa kitengo katika mraba tisa sawa, kuondoa mraba wa kati, kisha kufanya hivyo katika kila hatua kwa mraba ndogo iliyobaki. Takwimu inaonyesha kuweka iliyobaki baada ya iterations nne. Futa eneo la jumla lililoondolewa baada ya$ N$ hatua, na uhesabu urefu wa mzunguko wa jumla wa kuweka iliyobaki baada ya$ N$ hatua.

Jibu: Katika hatua moja mraba wa eneo$ 1/9$ huondolewa, kwa hatua$ 2$ moja huondoa$ 8$ mraba wa eneo$ 1/9^2$, katika hatua tatu huondoa$ 8^2$ mraba wa eneo$ 1/9^3$, na kadhalika. Eneo la jumla lililoondolewa baada ya$ N$ hatua ni$\displaystyle \sum_{n=0}^{N−1}\frac{8^N}{9^{N+1}}=\frac{1}{8}\cdot\frac{1−(8/9)^N}{1−8/9}→1$$N→∞.$ kama. mzunguko wa jumla ni$\displaystyle 4+4\sum_{n=0}^∞\frac{8^N}{3^{N+1}}→∞.$