9.3: Tofauti na Uchunguzi wa Integral

Malengo ya kujifunza

• Tumia mtihani wa kutofautiana ili kuamua kama mfululizo unajiunga au hupungua.
• Tumia mtihani muhimu ili kuamua ushirikiano wa mfululizo.
• Tathmini thamani ya mfululizo kwa kutafuta mipaka juu ya muda wake uliobaki.

Katika sehemu iliyopita, tuliamua muunganiko au tofauti ya mfululizo kadhaa kwa kuhesabu wazi kikomo cha mlolongo wa kiasi cha sehemu\( {S_k}.\) Katika mazoezi, kwa uwazi kuhesabu kikomo hiki inaweza kuwa vigumu au haiwezekani. Kwa bahati nzuri, vipimo kadhaa zipo ambazo zinatuwezesha kuamua muunganiko au tofauti kwa aina nyingi za mfululizo. Katika sehemu hii, tunazungumzia vipimo viwili hivi: mtihani wa tofauti na mtihani muhimu. Sisi kuchunguza vipimo vingine kadhaa katika mapumziko ya sura hii na kisha muhtasari jinsi na wakati wa kutumia yao.

Mtihani wa tofauti

Kwa mfululizo wa\(\displaystyle \sum^∞_{n=1}a_n\) kuungana,\( n^{th}\) neno\( a_n\) lazima kukidhi\( a_n→0\) kama\( n→∞.\) Kwa hiyo, kutoka algebraic kikomo mali ya Utaratibu,

\[\begin{align*} \lim_{k→∞}a_k = \lim_{k→∞}(S_k−S_{k−1}) \\[4pt] =\lim_{k→∞}S_k−\lim_{k→∞}S_{k−1} \\[4pt] =S−S=0. \end{align*}\]

Kwa hiyo, ikiwa\(\displaystyle \sum_{n=1}^∞a_n\) hujiunga,\( n^{th}\) neno\( a_n→0\)\( n→∞.\) kama Matokeo muhimu ya ukweli huu ni kauli ifuatayo:

Kama\( a_n↛0\) kama\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) diverges.

Jaribio hili linajulikana kama mtihani wa kutofautiana kwa sababu hutoa njia ya kuthibitisha kwamba mfululizo hupungua.

Ufafanuzi: Mtihani wa Tofauti

Ikiwa\(\displaystyle \lim_{n→∞}a_n=c≠0\) au\(\displaystyle \lim_{n→∞}a_n\) haipo, basi mfululizo\(\displaystyle \sum_{n=1}^∞a_n\) hupungua.

Ni muhimu kutambua kwamba mazungumzo ya theorem hii si kweli. Hiyo ni, kama\(\displaystyle \lim_{n→∞}a_n=0\), hatuwezi kufanya hitimisho lolote kuhusu muunganiko wa\(\displaystyle \sum_{n=1}^∞a_n\).

Kwa mfano,\(\displaystyle \lim_{n→0}\tfrac{1}{n}=0\), lakini mfululizo harmonic\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverges. Katika sehemu hii na sehemu iliyobaki ya sura hii, tunaonyesha mifano mingi zaidi ya mfululizo huo. Kwa hiyo, ingawa tunaweza kutumia mtihani wa kutofautiana kuonyesha kwamba mfululizo unatofautiana, hatuwezi kuitumia kuthibitisha kwamba mfululizo hujiunga. Hasa, kama\( a_n→0\), mtihani tofauti ni inconclusive.

Mfano\( \PageIndex{1}\): Using the divergence test

Kwa kila mfululizo wafuatayo, tumia mtihani wa kutofautiana. Kama mtihani tofauti inathibitisha kwamba mfululizo diverges, hali hivyo. Vinginevyo, zinaonyesha kwamba mtihani wa kutofautiana haujulikani.

1. \(\displaystyle \sum^∞_{n=1}\frac{n}{3n−1}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\)
3. \(\displaystyle \sum^∞_{n=1}e^{1/n^2}\)

Suluhisho

1. Kwa kuwa\(\displaystyle \lim_{n→∞} \frac{n}{3n−1}=\frac{1}{3}≠0\), kwa mtihani wa tofauti, tunaweza kuhitimisha kwamba\(\displaystyle \sum_{n=1}^∞\dfrac{n}{3n−1}\) hutofautiana.
2. Tangu\(\displaystyle \lim_{n→∞} \frac{1}{n^3}=0\), mtihani wa kutofautiana haujulikani.
3. Kwa kuwa\(\displaystyle \lim_{n→∞} e^{1/n^2}=1≠0\), kwa mtihani wa tofauti, mfululizo\(\displaystyle \sum_{n=1}^∞e^{1/n^2}\) hupungua.

Zoezi\( \PageIndex{1}\)

Mtihani wa tofauti unatuambia nini kuhusu mfululizo\(\displaystyle \sum_{n=1}^∞\cos(1/n^2)\)?

Kidokezo

Angalia\(\displaystyle \lim_{n→∞}\cos(1/n^2)\).

Jibu

Mfululizo hutofautiana.

Integral mtihani

Katika sehemu iliyopita, tumeonyesha kuwa mfululizo wa harmonic unatofautiana kwa kuangalia mlolongo wa kiasi cha sehemu\( {S_k}\) na kuonyesha kwamba\( S_{2^k}>1+k/2\) kwa integers zote nzuri\( k\). Katika sehemu hii tunatumia mbinu tofauti ili kuthibitisha tofauti ya mfululizo wa harmonic. Mbinu hii ni muhimu kwa sababu inatumika kuthibitisha tofauti au muunganiko wa mfululizo mwingine mingi. Mtihani huu, unaoitwa mtihani muhimu, unalinganisha jumla isiyo na kipimo kwa muhimu isiyofaa. Ni muhimu kutambua kwamba mtihani huu unaweza kutumika tu wakati tunazingatia mfululizo ambao maneno yake yote ni mazuri.

Kielelezo\(\PageIndex{1}\) : Jumla ya maeneo ya rectangles ni kubwa kuliko eneo kati ya curve\( f(x)=1/x\) na\( x\) -axis kwa\( x≥1\). Kwa kuwa eneo lililopakana na curve ni usio (kama ilivyohesabiwa na muhimu isiyofaa), jumla ya maeneo ya rectangles pia haipatikani.

Ili kuonyesha jinsi mtihani muhimu unavyofanya kazi, tumia mfululizo wa harmonic kama mfano. Katika Kielelezo\(\PageIndex{1}\), tunaonyesha mfululizo wa harmonic kwa kuchora mlolongo wa rectangles na maeneo\( 1,1/2,1/3,1/4,…\) pamoja na kazi\( f(x)=1/x.\) Kutoka kwenye grafu, tunaona hiyo

\[\sum_{n=1}^k\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+⋯+\dfrac{1}{k}>∫^{k+1}_1\dfrac{1}{x}\,dx. \nonumber \]

Kwa hiyo, kwa kila mmoja\( k\), jumla ya\( k^{\text{th}}\) sehemu\( S_k\) satisfies

\[\begin{align*} S_k =\sum_{n=1}^k\dfrac{1}{n} >∫^{k+1}_1\dfrac{1}{x}\,dx = \ln x \big| ^{k+1}_1 \\[4pt] = \ln (k+1)−\ln (1) \\[4pt] =\ln (k+1).\end{align*}\]

Kwa kuwa\(\displaystyle \lim_{k→∞}\ln(k+1)=∞,\) tunaona kwamba mlolongo wa kiasi cha sehemu\( {S_k}\) ni unbounded. Kwa hiyo,\( {S_k}\) hutofautiana, na, kwa hiyo, mfululizo\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n}\) pia hutofautiana.

Kielelezo\(\PageIndex{2}\): Jumla ya maeneo ya rectangles ni chini ya jumla ya eneo la mstatili wa kwanza na eneo kati ya curve\( f(x)=1/x^2\) na\( x\) -axis kwa\( x≥1\). Kwa kuwa eneo lililofungwa na curve ni la mwisho, jumla ya maeneo ya rectangles pia ni ya mwisho.

Sasa fikiria mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Tunaonyesha jinsi muhimu inaweza kutumika kuthibitisha kwamba mfululizo huu unajiunga. Katika Kielelezo\(\PageIndex{2}\), sisi mchoro mlolongo wa rectangles na maeneo\( 1,1/2^2,1/3^2,…\) pamoja na kazi\( f(x)=\frac{1}{x^2}\). Kutoka kwenye grafu tunaona hiyo

\[\sum_{n=1}^k\dfrac{1}{n^2}=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+⋯+\dfrac{1}{k^2}<1+∫^k_1\dfrac{1}{x^2}\,dx. \nonumber \]

Kwa hiyo, kwa kila mmoja\( k\), jumla ya\( k^{\text{th}}\) sehemu\( S_k\) satisfies

\[\begin{align*} S_k=\sum_{n=1}^k\dfrac{1}{n^2}<1+∫^k_1\dfrac{1}{x^2}\,dx =1−\left. \dfrac{1}{x} \right|^k_1 \\[4pt] =1−\dfrac{1}{k}+1 \\[4pt] =2−\dfrac{1}{k}<2. \end{align*}\]

Tunahitimisha kwamba mlolongo wa kiasi cha sehemu\( {S_k}\) ni imefungwa. Pia tunaona kwamba\( {S_k}\) ni mlolongo kuongezeka:

\[S_k=S_{k−1}+\dfrac{1}{k^2} \nonumber \]

kwa\( k≥2\).

Kwa kuwa\( {S_k}\) ni kuongezeka na imepakana, na Theorem Monotone Convergence, ni converges. Kwa hiyo, mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) hujiunga.

Kielelezo\(\PageIndex{3}\): (a) Kama tunaweza kuandika rectangles ndani ya mkoa imepakana\( y=f(x)\) na Curve na\( x\) -axis, na eneo imepakana na curves wale kwa\( x≥1\) ni ya mwisho, basi jumla ya maeneo ya mstatili pia ni ya mwisho. (b) Ikiwa seti ya mstatili huzunguka eneo lililopakana na\( x\) mhimili\( y=f(x)\) na eneo hilo lina eneo lisilo\( x≥1\) na mwisho, basi jumla ya maeneo ya mstatili pia hauna mwisho.

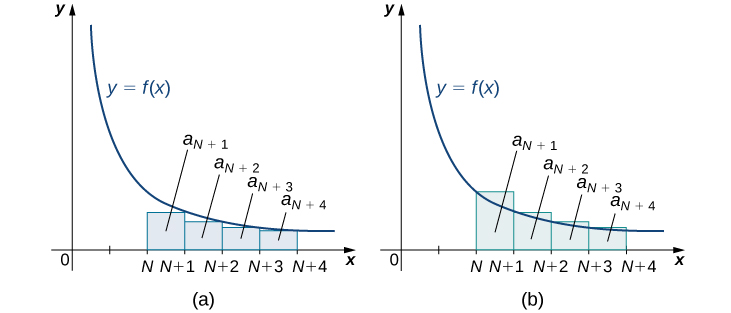
Tunaweza kupanua wazo hili kuthibitisha muunganiko au tofauti kwa mfululizo mbalimbali. Tuseme\(\displaystyle \sum^∞_{n=1}a_n\) ni mfululizo na maneno mazuri\( a_n\) kama vile kuna kazi inayoendelea, chanya, kupungua\( f\) ambapo\( f(n)=a_n\) kwa integers zote nzuri. Kisha, kama katika Kielelezo\(\PageIndex{3a}\), kwa integer yoyote\( k\), jumla ya\( k^{\text{th}}\) sehemu\( S_k\) satisfies

\[S_k=a_1+a_2+a_3+⋯+a_k<a_1+∫^k_1f(x)\,dx<1+∫^∞_1f(x)\,dx. \nonumber \]

Kwa hiyo, ikiwa\(\displaystyle ∫^∞_1f(x)\,dx\) hujiunga, basi mlolongo wa kiasi cha sehemu\( {S_k}\) ni imefungwa. Kwa kuwa\( {S_k}\) ni mlolongo kuongezeka, kama pia ni mlolongo imepakana, basi kwa Monotone Convergence Theorem, ni converges. Tunahitimisha kwamba ikiwa\(\displaystyle ∫^∞_1f(x)\,dx\) hujiunga, basi mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) pia hujiunga. Kwa upande mwingine, kutoka Kielelezo\(\PageIndex{3b}\), kwa integer yoyote\( k\), jumla ya\( k^{\text{th}}\) sehemu\( S_k\) satisfies

\[S_k=a_1+a_2+a_3+⋯+a_k>∫^{k+1}_1f(x)\,dx. \nonumber \]

Kama

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞, \nonumber \]

basi\( {S_k}\) ni mlolongo unbounded na hivyo diverges. Matokeo yake, mfululizo\(\displaystyle \sum_{n=1}^∞a_n\) pia unatofautiana. Tangu\( f\) ni kazi chanya, kama\(\displaystyle ∫^∞_1f(x)\,dx\) diverges, basi

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞. \nonumber \]

Tunahitimisha kwamba ikiwa\(\displaystyle ∫^∞_1f(x)\,dx\) hupungua, basi\(\displaystyle \sum_{n=1}^∞a_n\) hutofautiana.

Ufafanuzi: Mtihani wa Integral

Tuseme\(\displaystyle \sum_{n=1}^∞a_n\) ni mfululizo na maneno mazuri\( a_n\). Tuseme kuna kazi\( f\) na integer chanya\( N\) kama vile zifuatazo hali tatu ni kuridhika:

1. \( f\)ni endelevu,
2. \( f\)inapungua, na
3. \( f(n)=a_n\)kwa integers zote\( n≥N.\)

Kisha

\[\sum_{n=1}^∞a_n \nonumber \]

na

\[∫^∞_Nf(x)\,dx \nonumber \]

wote hujiunga au wote wawili wanatofautiana (Kielelezo\(\PageIndex{3}\)).

Ingawa kuunganishwa kwa\(\displaystyle ∫^∞_Nf(x)\,dx\) maana kuunganishwa kwa mfululizo unaohusiana\(\displaystyle \sum_{n=1}^∞a_n\), haimaanishi kwamba thamani ya muhimu na mfululizo ni sawa. Wanaweza kuwa tofauti, na mara nyingi ni. Kwa mfano,

\[\sum_{n=1}^∞\left(\dfrac{1}{e}\right)^n=\dfrac{1}{e}+\left(\dfrac{1}{e}\right)^2+\left(\dfrac{1}{e}\right)^3+⋯ \nonumber \]

ni mfululizo wa kijiometri na muda wa awali\( a=1/e\) na uwiano\( r=1/e,\) ambao hujiunga

\[\dfrac{1/e}{1−(1/e)}=\dfrac{1/e}{(e−1)/e}=\dfrac{1}{e−1}. \nonumber \]

Hata hivyo, muhimu kuhusiana\(\displaystyle ∫^∞_1(1/e)^x\,dx\) satisfies

\[∫^∞_1\left(\frac{1}{e}\right)^x\,dx=∫^∞_1e^{−x}\,dx=\lim_{b→∞}∫^b_1e^{−x}\,dx=\lim_{b→∞}−e^{−x}\big|^b_1=\lim_{b→∞}[−e^{−b}+e^{−1}]=\dfrac{1}{e}. \nonumber \]

Mfano\( \PageIndex{2}\): Using the Integral Test

Kwa kila moja ya mfululizo wafuatayo, tumia mtihani muhimu ili uone kama mfululizo unajiunga au hupungua.

1. \(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{\sqrt{2n−1}}\)

Suluhisho

a. kulinganisha

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\)na\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx.\)

Tuna

\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\bigg|^b_1\right]=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2}\right]=\dfrac{1}{2}.\)

Hivyo, muhimu\(\displaystyle ∫^∞_1\frac{1}{x^3}\,dx\) hujiunga, na kwa hiyo mfululizo

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\).

b. kulinganisha

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{\sqrt{2n−1}}\)na\(\displaystyle ∫^∞_1\dfrac{1}{\sqrt{2x−1}}\,dx\).

Tangu

\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}∫^b_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}\sqrt{2x−1}\bigg|^b_1=\lim_{b→∞}\left[\sqrt{2b−1}−1\right]=∞,\)

\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx\)diverges muhimu, na kwa hiyo

\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{2n−1}}\)

hutengana.

Zoezi\( \PageIndex{2}\)

Tumia mtihani muhimu ili kuamua kama mfululizo\(\displaystyle \sum^∞_{n=1}\dfrac{n}{3n^2+1}\) unajiunga au hupungua.

Kidokezo

Linganisha na muhimu\(\displaystyle ∫^∞_1\dfrac{x}{3x^2+1}\,dx.\)

Jibu

Mfululizo hutofautiana.

\(p\)-Series

Mfululizo wa harmonic\(\displaystyle \sum^∞_{n=1}1/n\) na mfululizo\(\displaystyle \sum^∞_{n=1}1/n^2\) ni mifano yote ya aina ya mfululizo inayoitwa p-mfululizo.

Ufafanuzi:\(p\)-series

Kwa idadi yoyote halisi\( p\), mfululizo

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

inaitwa p-mfululizo.

Tunajua\(p\) -mfululizo hujiunga kama\( p=2\) na diverges kama\( p=1\). Nini kuhusu maadili mengine ya\( p\)? Kwa ujumla, ni vigumu, ikiwa haiwezekani, kuhesabu thamani halisi ya\( p\) mfululizo wengi. Hata hivyo, tunaweza kutumia vipimo iliyotolewa hadi sasa ili kuthibitisha kama\( p\) -mfululizo hujiunga au hutofautiana.

Kama\( p<0,\) basi\( 1/n^p→∞,\) na kama\( p=0\), basi\( 1/n^p→1.\) Kwa hiyo, kwa mtihani tofauti,

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

hutofautiana kama\(p≤0\).

Ikiwa\( p>0,\) basi\( f(x)=1/x^p\) ni kazi nzuri, inayoendelea, inayopungua. Kwa hiyo, kwa\( p>0,\) sisi kutumia mtihani muhimu, kulinganisha

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]na\[∫^∞_1\dfrac{1}{x^p}\,dx. \nonumber \]

Sisi tayari kuchukuliwa kesi wakati\( p=1.\) Hapa tunaona kesi wakati\( p>0,p≠1.\) Kwa kesi hii,

\[∫^∞_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}\dfrac{1}{1−p}x^{1−p}∣^b_1=\lim_{b→∞}\dfrac{1}{1−p}[b^{1−p}−1]. \nonumber \]

Kwa sababu

\( b^{1−p}→0\)kama\( p>1\) na\( b^{1−p}→∞\) kama\( p<1,\)

tunahitimisha kwamba

\[∫^∞_1\dfrac{1}{x^p}\,dx=\begin{cases}\dfrac{1}{p−1}, \text{if}\;p>1\\ ∞, \text{if}\;p<1.\end{cases} \nonumber \]

Kwa hiyo,\(\displaystyle \sum^∞_{n=1}1/n^p\) converges kama\( p>1\) na diverges kama\( 0<p<1.\)

Kwa muhtasari,

\[\sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges} \text{if}\; p>1\\ \text{diverges} \text{if}\;p≤1\end{cases} \nonumber \].

Mfano\( \PageIndex{3}\): Testing for Convergence of p-series

Kwa kila moja ya mfululizo wafuatayo, onyesha ikiwa hujiunga au hupungua.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^4}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{2/3}}\)

Suluhisho

1. Hii ni\(p\) -mfululizo na\( p=4>1\), hivyo mfululizo hujiunga.
2. Tangu\( p=2/3<1,\) mfululizo hupungua.

Zoezi\( \PageIndex{3}\)

Je! Mfululizo\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{5/4}}\) hujiunga au hutofautiana?

Kidokezo

\( p=5/4\)

Jibu

Mfululizo hujiunga.

Kukadiria Thamani ya Mfululizo

Tuseme tunajua kwamba mfululizo\(\displaystyle \sum_{n=1}^∞a_n\) hujiunga na tunataka kukadiria jumla ya mfululizo huo. Hakika tunaweza takriban kwamba jumla kwa kutumia jumla yoyote finite\(\displaystyle \sum_{n=1}^Na_n\) ambapo\( N\) ni integer yoyote chanya. swali sisi kushughulikia hapa ni, kwa mfululizo convergent\(\displaystyle \sum^∞_{n=1}a_n\), jinsi nzuri ni makadirio\(\displaystyle \sum^N_{n=1}a_n\)?

Zaidi hasa, kama sisi basi

\[R_N=\sum_{n=1}^∞a_n−\sum_{n=1}^Na_n \nonumber \]

kuwa salio wakati jumla ya mfululizo usio ni approximated na jumla ya\(N^{\text{th}}\) sehemu, jinsi kubwa ni\( R_N\)? Kwa aina fulani za mfululizo, tunaweza kutumia mawazo kutoka kwa mtihani muhimu ili kukadiria\( R_N\).

Kumbuka\(\PageIndex{1}\): Remainder Estimate from the Integral Test

Tuseme\(\displaystyle \sum^∞_{n=1}a_n\) ni mfululizo convergent na maneno chanya. Tuseme kuna kazi ya\( f\) kuridhisha masharti matatu yafuatayo:

1. \( f\)ni endelevu,
2. \( f\)inapungua, na
3. \( f(n)=a_n\)kwa integers zote\( n≥1.\)

Hebu\( S_N\) kuwa jumla ya\(N^{\text{th}}\) sehemu ya\(\displaystyle \sum^∞_{n=1}a_n\). Kwa integers wote chanya\( N\),

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Kwa maneno mengine, salio\(\displaystyle R_N=\sum^∞_{n=1}a_n−S_N=\sum^∞_{n=N+1}a_n\) linatimiza makadirio yafuatayo:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Hii inajulikana kama makadirio ya salio.

Sisi kuonyesha Kumbuka\(\PageIndex{1}\) katika Kielelezo\(\PageIndex{4}\). Hasa, kwa kuwakilisha salio\( R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯\) kama jumla ya maeneo ya rectangles, tunaona kwamba eneo la rectangles wale ni imepakana juu\(\displaystyle ∫^∞_Nf(x)\,dx\) na imepakana chini na Kwa maneno mengine,\(\displaystyle ∫^∞_{N+1}f(x)\,dx.\)

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx \nonumber \]

na

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx. \nonumber \]

Sisi kuhitimisha kwamba

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Tangu

\[\sum_{n=1}^∞a_n=S_N+R_N, \nonumber \]

\( S_N\)wapi jumla ya\(N^{\text{th}}\) sehemu, tunahitimisha kuwa

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Kielelezo\(\PageIndex{4}\): Kutokana\( f\) na kazi inayoendelea, chanya, kupungua na mlolongo wa maneno mazuri\( a_n\) kama vile\( a_n=f(n)\) kwa integers zote nzuri\( n\), (a) maeneo\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx\), au (b) maeneo\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx\). Kwa hiyo, muhimu ni ama overestimate au underestimate ya kosa.

Mfano\( \PageIndex{4}\): Estimating the Value of a Series

Fikiria mfululizo\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\).

1. Tumia\(\displaystyle S_{10}=\sum^{10}_{n=1}\frac{1}{n^3}\) na ukadiria kosa.
2. Kuamua thamani angalau ya\( N\) muhimu kama kwamba\( S_N\) makadirio\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\) ya ndani\( 0.001\).

Suluhisho

a Kutumia matumizi ya kuhesabu, tuna

\[ S_{10}=1+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3}+⋯+\dfrac{1}{10^3}≈1.19753. \nonumber \]

Kwa makadirio ya salio, tunajua

\[ R_N<∫^∞_N\dfrac{1}{x^3}\,dx. \nonumber \]

Tuna

\[ ∫^∞_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\right]^b_N=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2N^2}\right]=\dfrac{1}{2N^2}. \nonumber \]

Kwa hiyo, hitilafu ni\( R_{10}<1/2(10)^2=0.005.\)

b Kupata\( N\) vile kwamba\( R_N<0.001\). Katika sehemu ya a. tulionyesha kuwa\( R_N<1/2N^2\). Kwa hiyo, salio kwa muda mrefu\( R_N<0.001\) kama\( 1/2N^2<0.001\). Hiyo ni, tunahitaji\( 2N^2>1000\). Kutatua usawa huu kwa\( N\), tunaona kwamba tunahitaji\( N>22.36\). Ili kuhakikisha kwamba salio ni ndani ya kiasi kilichohitajika, tunahitaji kuzunguka hadi integer iliyo karibu. Kwa hiyo, thamani ya chini ya lazima ni\( N=23\).

Zoezi\( \PageIndex{4}\)

Kwa\(\displaystyle \sum^∞_{n=1}\frac{1}{n^4}\), mahesabu\( S_5\) na kukadiria makosa\( R_5\).

Kidokezo

Tumia makadirio yaliyobaki\(\displaystyle R_N<∫^∞_N\frac{1}{x^4}\,dx.\)

Jibu

\( S_5≈1.09035, R_5<0.00267\)

Dhana muhimu

• Ikiwa\(\displaystyle \lim_{n→∞}a_n≠0,\) basi mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) hupungua.
• Kama\(\displaystyle \lim_{n→∞}a_n=0,\) mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) inaweza kugeuza au tofauti.
• Ikiwa\(\displaystyle \sum^∞_{n=1}a_n\) ni mfululizo na maneno mazuri\( a_n\) na\( f\) ni kazi inayoendelea, ya kupungua kama vile\( f(n)=a_n\) kwa integers zote nzuri\( n\), basi

\[\sum_{n=1}^∞a_n \nonumber \]na\[∫^∞_1f(x)\,dx \nonumber \]

ama wote hujiunga au wote wawili wanatofautiana. Zaidi ya hayo, kama\(\displaystyle \sum^∞_{n=1}a_n\) converges, kisha\(N^{\text{th}}\) sehemu jumla makadirio\( S_N\) ni sahihi hadi makosa\( R_N\) ambapo\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\).

• \(p\)-mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^p}\) hujiunga kama\( p>1\) na diverges kama\( p≤1.\)

Mlinganyo muhimu

• Mtihani wa tofauti

Kama\( a_n↛0\) kama\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) diverges.

• p-mfululizo

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges}, \text{if}\;p>1\\\text{diverges}, \text{if}\; p≤1\end{cases}\)

• Makadirio ya salio kutoka kwa mtihani muhimu

\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\)

faharasa

mtihani wa muachano

ikiwa\(\displaystyle \lim_{n→∞}a_n≠0,\) basi mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unapungua

mtihani muhimu

kwa mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) na maneno mazuri\( a_n\), ikiwa kuna kazi inayoendelea, ya kupungua\( f\) kama vile\( f(n)=a_n\) kwa integers zote nzuri\( n\), basi

\[\sum_{n=1}^∞a_n \nonumber \]na\[∫^∞_1f(x)\,dx \nonumber \]

ama wote hujiunga au wote wawili wanatofautiana

p -mfululizo

mfululizo wa fomu\(\displaystyle \sum^∞_{n=1}1/n^p\)

makadirio yaliyobaki

kwa mfululizo\(\displaystyle \sum^∞_{n=}1a_n\) na maneno\( a_n\) mazuri na kazi inayoendelea, ya kupungua\( f\) kama vile\( f(n)=a_n\) kwa integers zote nzuri\( n\), salio\(\displaystyle R_N=\sum^∞_{n=1}a_n−\sum^N_{n=1}a_n\) hutimiza makadirio yafuatayo:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx \nonumber \]