10.3: Resolva equações quadráticas usando a fórmula quadrática
- Page ID
- 184127
Ao final desta seção, você poderá:
- Resolva equações quadráticas usando a fórmula quadrática
- Use o discriminante para prever o número de soluções de uma equação quadrática
- Identifique o método mais apropriado a ser usado para resolver uma equação quadrática
Quando resolvemos equações quadráticas na última seção completando o quadrado, sempre demos os mesmos passos. Ao final do conjunto de exercícios, você deve estar se perguntando “não há uma maneira mais fácil de fazer isso?” A resposta é “sim”. Nesta seção, derivaremos e usaremos uma fórmula para encontrar a solução de uma equação quadrática.
Já vimos como resolver uma fórmula para uma variável específica 'em geral' para que façamos as etapas algébricas apenas uma vez e depois usássemos a nova fórmula para encontrar o valor da variável específica. Agora, passaremos pelas etapas de completar o quadrado em geral para resolver uma equação quadrática para x. Pode ser útil examinar um dos exemplos no final da última seção em que resolvemos uma equação do formulário\( ax^2+bx+c=0\) enquanto você lê as etapas algébricas abaixo, para que você as veja com números e “em geral”.
| Começamos com a forma padrão de uma equação quadrática e a resolvemos para x completando o quadrado. | \( ax^2+bx+c=0\) | |
| Isole os termos variáveis em um lado. | \( ax^2+bx=−c\) | |
| Faça o coeficiente inicial 1, dividindo por a. | \(\frac{ax^2}{a}+\frac{b}{a}x=−\frac{c}{a}\) | |
| Simplifique. | \(x^2+\frac{b}{a}x=−\frac{c}{a}\) | |
|
Para completar o quadrado, encontre\((\frac{1}{2}·\frac{b}{a})^2\) e adicione-o aos dois lados da equação. \((\frac{1}{2}\frac{b}{a})^2=\frac{b^2}{4a^2}\) |
\(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| O lado esquerdo é um quadrado perfeito, considere-o. | \((x+\frac{b}{2a})^2=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| Encontre o denominador comum do lado direito e escreva frações equivalentes com o denominador comum. | \((x+\frac{b}{2a})^2=−\frac{c·4a}{a·4a}+\frac{b^2}{4a^2}\) | |
| Simplifique. | \((x+\frac{b}{2a})^2=\frac{b^2}{4a^2}−\frac{4ac}{4a^2}\) | |
| Combine em uma fração. | \((x+\frac{b}{2a})^2=\frac{b^2−4ac}{4a^2}\) | |
| Use a propriedade raiz quadrada. | \((x+\frac{b}{2a})=\pm\sqrt{\frac{b^2−4ac}{4a^2}}\) | |
| Simplifique. | \((x+\frac{b}{2a})=\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| Adicione\(−\frac{b}{2a} \) aos dois lados da equação. | \(x=−\frac{b}{2a}\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| Combine os termos no lado direito. | \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) | |
Essa última equação é a Fórmula Quadrática.
As soluções para uma equação quadrática da forma\(ax^2+bx+c=0\)\(a\ge 0\) são dadas pela fórmula:
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
Para usar a Fórmula Quadrática, substituímos os valores de a, b e c na expressão no lado direito da fórmula. Em seguida, fazemos todas as contas para simplificar a expressão. O resultado fornece a (s) solução (s) para a equação quadrática.
Como resolver uma equação quadrática usando a fórmula quadrática
Resolva\(2x^2+9x−5=0\) usando a Fórmula Quadrática.
- Resposta
-


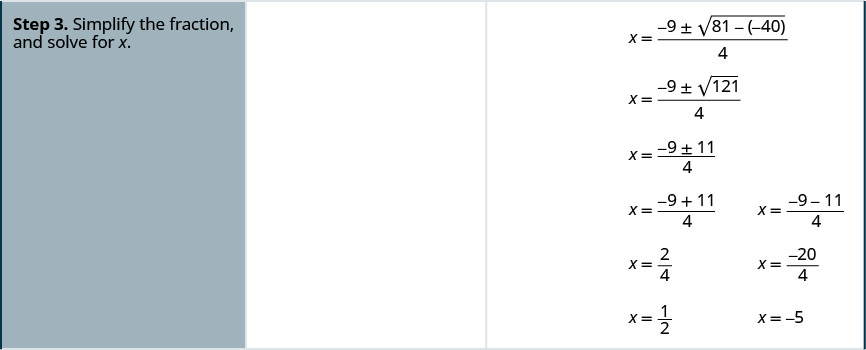

Resolva\(3y^2−5y+2=0\) usando a Fórmula Quadrática.
- Resposta
-
\(y=\frac{2}{3}\),\(y=1\)
Resolva\(4z^2+2z−6=0\) usando a Fórmula Quadrática.
- Resposta
-
\(z=−\frac{3}{2}\),\(z=1\)
- Escreva a fórmula quadrática na forma padrão. Identifique os valores aa, bb e cc.
- Escreva a fórmula quadrática. Em seguida, substitua os valores de a, b e c.
- Simplifique.
- Verifique as soluções.
Se você disser a fórmula à medida que a escreve em cada problema, você a memorizará em pouco tempo. E lembre-se, a Fórmula Quadrática é uma equação. Certifique-se de começar com '\(x=\)'.
Resolva\(x^2−6x+5=0\) usando a Fórmula Quadrática.
- Resposta
-

Essa equação está na forma padrão. 
Identifique os valores a, b, c. 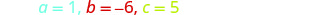
Escreva a fórmula quadrática. 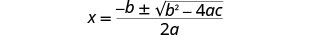
Em seguida, substitua os valores de a, b, c. 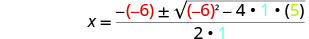
Simplifique. 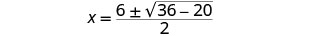
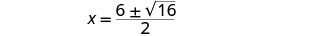
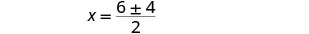
Reescreva para mostrar duas soluções. 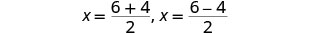
Simplifique. 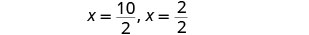
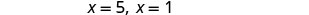
Verifique.
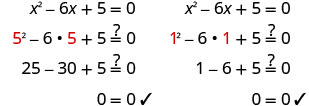
Resolva\(a^2−2a−15=0\) usando a Fórmula Quadrática.
- Resposta
-
\(a=−3\),\(a=5\)
Resolva\(b^2+10b+24=0\) usando a Fórmula Quadrática.
- Resposta
-
\(b=−6\),\(b=−4\)
Quando resolvemos equações quadráticas usando a propriedade de raiz quadrada, às vezes obtivemos respostas que tinham radicais. Isso também pode acontecer ao usar a Fórmula Quadrática. Se obtivermos um radical como solução, a resposta final deve ter o radical em sua forma simplificada.
Resolva\(4y^2−5y−3=0\) usando a Fórmula Quadrática.
- Resposta
-
Podemos usar a Fórmula Quadrática para resolver a variável em uma equação quadrática, seja ela chamada de 'x'.

Essa equação está na forma padrão. 
Identifique os valores a, b, c. 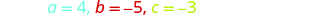
Escreva a fórmula quadrática. 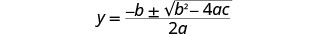
Em seguida, substitua os valores de a, b, c. 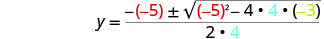
Simplifique. 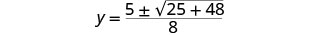
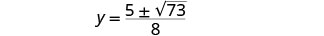
Reescreva para mostrar duas soluções. 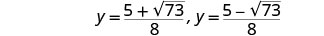
Verifique. Deixamos o cheque para você.
Resolva\(2p^2+8p+5=0\) usando a Fórmula Quadrática.
- Resposta
-
\(p=\frac{−4\pm\sqrt{6}}{2}\)
Resolva\(5q^2−11q+3=0\) usando a Fórmula Quadrática.
- Resposta
-
\(q=\frac{11\pm\sqrt{61}}{10}\)
Resolva\(2x^2+10x+11=0\) usando a Fórmula Quadrática.
- Resposta
-

Essa equação está na forma padrão. 
Identifique os valores a, b, c. 
Escreva a fórmula quadrática. 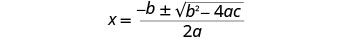
Em seguida, substitua os valores de a, b, c. 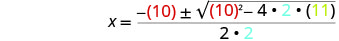
Simplifique. 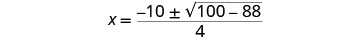
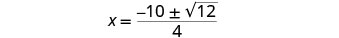
Simplifique o radical. 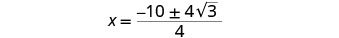
Considere o fator comum no numerador. 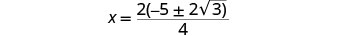
Remova os fatores comuns. 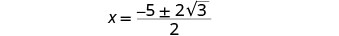
Reescreva para mostrar duas soluções. 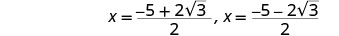
Verifique. Deixamos o cheque para você.
Resolva\(3m^2+12m+7=0\) usando a Fórmula Quadrática.
- Resposta
-
\(m=\frac{−6\pm\sqrt{15}}{3}\)
Resolva\(5n^2+4n−4=0\) usando a Fórmula Quadrática.
- Resposta
-
\(n=\frac{−2\pm2\sqrt{6}}{5}\)
Não podemos pegar a raiz quadrada de um número negativo. Então, quando substituímos a, b e c na Fórmula Quadrática, se a quantidade dentro do radical for negativa, a equação quadrática não tem solução real. Veremos isso no próximo exemplo.
Resolva\(3p^2+2p+9=0\) usando a Fórmula Quadrática.
- Resposta
-
Essa equação está na forma padrão. 
Identifique os valores a, b, c. 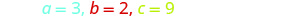
Escreva a fórmula quadrática. 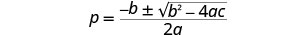
Em seguida, substitua os valores de a, b, c. 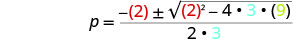
Simplifique. 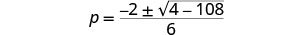
Simplifique o radical. 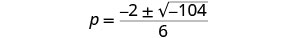
Não podemos pegar a raiz quadrada de um número negativo. Não existe uma solução real.
Resolva\(4a^2−3a+8=0\) usando a Fórmula Quadrática.
- Resposta
-
nenhuma solução real
Resolva\(5b^2+2b+4=0\) usando a Fórmula Quadrática.
- Resposta
-
nenhuma solução real
As equações quadráticas que resolvemos até agora nesta seção foram todas escritas na forma padrão,\(ax^2+bx+c=0\). Às vezes, precisaremos fazer alguma álgebra para colocar a equação na forma padrão antes de podermos usar a Fórmula Quadrática.
Resolva\(x(x+6)+4=0\) usando a Fórmula Quadrática.
- Resposta
-

Distribua para obter a equação na forma padrão. 
Essa equação agora está na forma padrão. 
Identifique os valores a, b, c. 
Escreva a fórmula quadrática. 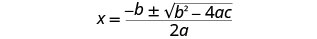
Em seguida, substitua os valores de a, b, c. 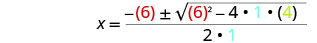
Simplifique. 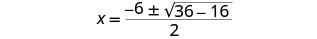
Simplifique o interior do radical. 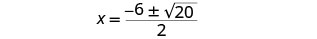
Simplifique o radical. 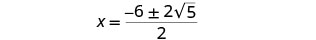
Considere o fator comum no numerador. 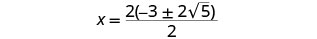
Remova os fatores comuns. 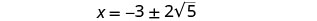
Reescreva para mostrar duas soluções. 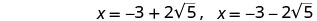
Verifique. Deixamos o cheque para você.
Resolva\(x(x+2)−5=0\) usando a Fórmula Quadrática.
- Resposta
-
\(x=−1\pm\sqrt{6}\)
Resolva\(y(3y−1)−2=0\) usando a Fórmula Quadrática.
- Resposta
-
\(y=−\frac{2}{3}\),\(y=1\)
Quando resolvemos equações lineares, se uma equação tivesse muitas frações, “eliminamos as frações” multiplicando os dois lados da equação pelo LCD. Isso nos deu uma equação equivalente — sem frações — para resolver. Podemos usar a mesma estratégia com equações quadráticas.
Resolva\(\frac{1}{2}u^2+\frac{2}{3}u=\frac{1}{3}\) usando a Fórmula Quadrática.
- Resposta
-
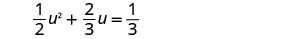
Multiplique os dois lados pelo LCD, 6, para limpar as frações. 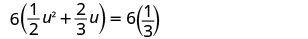
Multiplique. 
Subtraia 2 para obter a equação na forma padrão. 
Identifique os valores a, b, c. 
Escreva a fórmula quadrática. 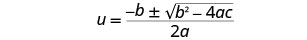
Em seguida, substitua os valores de a, b, c. 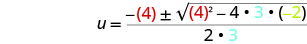
Simplifique. 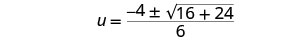
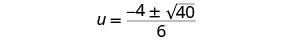
Simplifique o radical. 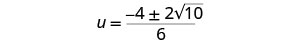
Considere o fator comum no numerador. 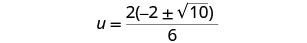
Remova os fatores comuns. 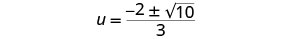
Reescreva para mostrar duas soluções. 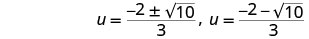
Verifique. Deixamos o cheque para você.
Resolva\(\frac{1}{4}c^2−\frac{1}{3}c=\frac{1}{12}\) usando a Fórmula Quadrática.
- Resposta
-
\(c=\frac{2\pm\sqrt{7}}{3}\)
Resolva\(\frac{1}{9}d^2−\frac{1}{2}d=−\frac{1}{2}\) usando a Fórmula Quadrática.
- Resposta
-
\(d=\frac{3}{2}\),\(d=3\)
Pense na equação\((x−3)^2=0\). We know from the Zero Products Principle that this equation has only one solution: \(x=3\).
Veremos no próximo exemplo como usar a Fórmula Quadrática para resolver uma equação com um quadrado perfeito também fornece apenas uma solução.
Resolva\(4x^2−20x=−25\) usando a Fórmula Quadrática.
- Resposta
-

Adicione 25 para obter a equação na forma padrão. 
Identifique os valores a, b, c. 
Escreva a fórmula quadrática. 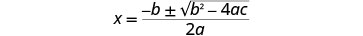
Em seguida, substitua os valores de a, b, c. 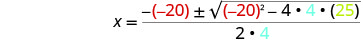
Simplifique. 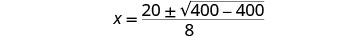
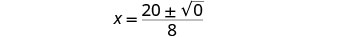
Simplifique o radical. 
Simplifique a fração. 
Verifique. Deixamos o cheque para você. Você reconheceu que\(4x^2−20x+25\) é um quadrado perfeito?
Resolva\(r^2+10r+25=0\) usando a Fórmula Quadrática.
- Resposta
-
\(r=−5\)
Resolva\(25t^2−40t=−16\) usando a Fórmula Quadrática.
- Resposta
-
\(t=\frac{4}{5}\)
Use o discriminante para prever o número de soluções de uma equação quadrática
Quando resolvemos as equações quadráticas nos exemplos anteriores, às vezes obtivemos duas soluções, às vezes uma solução, às vezes nenhuma solução real. Existe uma maneira de prever o número de soluções para uma equação quadrática sem realmente resolver a equação?
Sim, a quantidade dentro do radical da Fórmula Quadrática facilita a determinação do número de soluções. Essa quantidade é chamada de discriminante.
Na Fórmula Quadrática\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\), a quantidade\(b^2−4ac\) é chamada de discriminante.
Vamos examinar o discriminante das equações em Exemplo, Exemplo e Exemplo e o número de soluções para essas equações quadráticas.
| Equação quadrática (na forma padrão) | Discriminante\(b^2−4ac\) | Sinal do Discriminante | Número da solução real | |
|---|---|---|---|---|
| Exemplo | \(2x^2+9x−5=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\(9^2−4·2(−5)=121\) | + | 2 |
| Exemplo | \(4x^2−20x+25=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\((−20)^2−4·4·25=0\) | 0 | 1 |
| Exemplo | \(3p^2+2p+9=0\) | \ (b^2−4ac\)” data-valign="middle” class="lt-math-15194">\(2^2−4·3·9=−104\) | − | 0 |
Quando o discriminante é positivo,\(x=\frac{−b\pm\sqrt{+}}{2a}\) a equação quadrática tem duas soluções.
Quando o discriminante é zero,\(x=\frac{−b\pm\sqrt{0}}{2a}\) a equação quadrática tem uma solução.
Quando o discriminante é negativo,\(x=\frac{−b\pm\sqrt{−}}{2a}\) a equação quadrática não tem soluções reais.
Para uma equação quadrática da forma\(ax^2+bx+c=0\),\(a \ge 0\),
- se\(b^2−4ac>0\), a equação tem duas soluções.
- se\(b^2−4ac=0\), a equação tem uma solução.
- se\(b^2−4ac<0\), a equação não tem soluções reais.
Determine o número de soluções para cada equação quadrática:
- \(2v^2−3v+6=0\)
- \(3x^2+7x−9=0\)
- \(5n^2+n+4=0\)
- \(9y^2−6y+1=0\)
- Resposta
-
1.
\(2v^2−3v+6=0\) A equação está na forma padrão, identifique a, b, c. \(a=2\),\(b=−3\),\(c=6\) Escreva o discriminante. \(b^2−4ac\) Substitua os valores de a, b, c. \((3)^2−4·2·6\) Simplifique. \(9−48\)
\(−39\)
Como o discriminante é negativo, não há soluções reais para a equação. 2.
\(3x^2+7x−9=0\) A equação está na forma padrão, identifique a, b, c. \(a=3\),\(b=7\),\(c=−9\) Escreva o discriminante. \(b^2−4ac\) Substitua os valores de a, b, c. \((7)^2−4·3·(−9)\) Simplifique. \(49+108\)
\(157\)
Como o discriminante é positivo, existem duas soluções para a equação. 3.
\(5n^2+n+4=0\) A equação está na forma padrão, identifique a, b, c. \(a=5\),\(b=1\),\(c=4\) Escreva o discriminante. \(b^2−4ac\) Substitua os valores de a, b, c. \((1)^2−4·5·4\) Simplifique. \(1−80\)
\(−79\)
Como o discriminante é negativo, não há soluções reais para a equação. 4.
\(9y^2−6y+1=0\) A equação está na forma padrão, identifique a, b, c. \(a=9\),\(b=−6\),\(c=1\) Escreva o discriminante. \(b^2−4ac\) Substitua os valores de a, b, c. \((−6)^2−4·9·1\) Simplifique. \(36−36\)
\(0\)
Como o discriminante é 0, há uma solução para a equação.
Determine o número de soluções para cada equação quadrática:
- \(8m^2−3m+6=0\)
- \(5z^2+6z−2=0\)
- \(9w^2+24w+16=0\)
- \(9u^2−2u+4=0\)
- Resposta
-
- sem soluções reais
- 2
- 1
- sem soluções reais
Determine o número de soluções para cada equação quadrática:
- \( b^2+7b−13=0\)
- \(5a^2−6a+10=0\)
- \(4r^2−20r+25=0\)
- \(7t^2−11t+3=0\)
- Resposta
-
- 2
- sem soluções reais
- 1
- 2
Identifique o método mais apropriado a ser usado para resolver uma equação quadrática
Usamos quatro métodos para resolver equações quadráticas:
- Fatorar
- Propriedade de raiz quadrada
- Completando a Praça
- Fórmula quadrática
Você pode resolver qualquer equação quadrática usando a Fórmula Quadrática, mas esse nem sempre é o método mais fácil de usar.
- Experimente o Factoring primeiro. Se os fatores quadráticos forem fáceis, esse método é muito rápido.
- Em seguida, experimente a propriedade Square Root. Se a equação se encaixa na forma\(ax^2=k\) ou\(a(x−h)^2=k\), ela pode ser facilmente resolvida usando a propriedade de raiz quadrada.
- Use a fórmula quadrática. Qualquer equação quadrática pode ser resolvida usando a Fórmula Quadrática.
E quanto ao método de completar o quadrado? A maioria das pessoas acha esse método complicado e prefere não usá-lo. Precisávamos incluí-lo neste capítulo porque completamos o quadrado em geral para derivar a Fórmula Quadrática. Você também usará o processo de completar o quadrado em outras áreas da álgebra.
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática:
- \(5z^2=17\)
- \(4x^2−12x+9=0\)
- \(8u^2+6u=11\)
- Resposta
-
1. \(5z^2=17\)
Como a equação está no\(ax^2=k\), o método mais apropriado é usar a propriedade de raiz quadrada.
2. \(4x^2−12x+9=0\)
Reconhecemos que o lado esquerdo da equação é um trinômio quadrado perfeito e, portanto, a fatoração será o método mais apropriado.
3. \(8u^2+6u=11\)
Coloque a equação na forma padrão. \(8u^2+6u−11=0\)
Embora nosso primeiro pensamento seja tentar fatorar, pensar em todas as possibilidades de tentativa e erro nos leva a escolher a Fórmula Quadrática como o método mais apropriado.
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática:
- \(x^2+6x+8=0\)
- \((n−3)^2=16\)
- \(5p^2−6p=9\)
- Resposta
-
- fatorar
- Propriedade de raiz quadrada
- Fórmula quadrática
Identifique o método mais apropriado a ser usado para resolver cada equação quadrática:
- \(8a^2+3a−9=0\)
- \(4b^2+4b+1=0\)
- \(5c2=125\)
- Resposta
-
- Fórmula quadrática
- fatorar
- Propriedade de raiz quadrada
Acesse esses recursos on-line para obter instruções e práticas adicionais com o uso da Fórmula Quadrática:
- Resolvendo equações quadráticas: resolvendo com a fórmula quadrática
- Como resolver uma equação quadrática na forma padrão usando a Fórmula Quadrática (exemplo)
- Resolvendo equações quadráticas usando a fórmula quadrática—Exemplo 3
- Resolva equações quadráticas usando a fórmula quadrática
Conceitos chave
- Fórmula quadrática As soluções para uma equação quadrática da forma\(ax^2+bx+c=0\)\(a \ge 0\) são dadas pela fórmula:
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
- Resolva uma equação quadrática usando a fórmula quadrática
Para resolver uma equação quadrática usando a fórmula quadrática.- Escreva a fórmula quadrática na forma padrão. Identifique os valores a, b, c.
- Escreva a fórmula quadrática. Em seguida, substitua os valores de a, b, c.
- Simplifique.
- Verifique as soluções.
- Usando o discriminante,\(b^2−4ac\), para determinar o número de soluções de uma equação quadrática
Para uma equação quadrática da forma\(ax^2+bx+c=0\),\(a \ge 0\),- se\(b^2−4ac>0\), a equação tem 2 soluções.
- se\(b^2−4ac=0\), a equação tem 1 solução.
- se\(b^2−4ac<0\), a equação não tem soluções reais.
- Para identificar o método mais adequado para resolver uma equação quadrática:
- Experimente o Factoring primeiro. Se os fatores quadráticos forem fáceis, esse método é muito rápido.
- Experimente a propriedade Square Root em seguida. Se a equação se encaixa na forma\(ax^2=k\) ou\(a(x−h)^2=k\), ela pode ser facilmente resolvida usando a propriedade de raiz quadrada.
- Use a fórmula quadrática. Qualquer outra equação quadrática é melhor resolvida usando a Fórmula Quadrática.
Glossário
- discriminante
- Na Fórmula Quadrática,\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) a quantidade\(b^2−4ac\) é chamada de discriminante.


