10.2: Resolva equações quadráticas completando o quadrado
- Page ID
- 184126
Ao final desta seção, você poderá:
- Complete o quadrado de uma expressão binomial
- Resolva equações quadráticas do formulário\(x^2+bx+c=0\) completando o quadrado
- Resolva equações quadráticas do formulário\(ax^2+bx+c=0\) completando o quadrado
Antes de começar, faça este teste de prontidão. Se você perder algum problema, volte para a seção listada e revise o material.
- Simplifique\((x+12)^2\).
Se você perdeu esse problema, consulte o Exemplo 6.4.1. - Fator\(y^2−18y+81\).
Se você perdeu esse problema, revise o Exercício 7.4.1. - Fator\(5n^2+40n+80\).
Se você perdeu esse problema, revise o Exercício 7.4.13.
Até agora, resolvemos equações quadráticas fatorando e usando a propriedade de raiz quadrada. Nesta seção, resolveremos equações quadráticas por meio de um processo chamado “completar o quadrado”.
Complete o quadrado de uma expressão binomial
Na última seção, pudemos usar a propriedade de raiz quadrada para resolver a equação\((y−7)^2=12\) porque o lado esquerdo era um quadrado perfeito.
\[\begin{array}{l} {(y−7)^2=12}\\ {y−7=\pm\sqrt{12}}\\ {y−7=\pm2\sqrt{3}}\\ {y=7\pm2\sqrt{3}}\\ \nonumber \end{array}\]
Também resolvemos uma equação na qual o lado esquerdo era um trinômio quadrado perfeito, mas tivemos que reescrevê-lo\((x−k)^2\) na forma para usar a propriedade da raiz quadrada.
\[\begin{array}{l} {x^2−10x+25=18}\\ {(x−5)^2=18}\\ \nonumber \end{array}\]
O que acontece se a variável não fizer parte de um quadrado perfeito? Podemos usar álgebra para fazer um quadrado perfeito?
Vamos estudar o padrão binomial quadrado que usamos muitas vezes. Vamos ver dois exemplos.
\[\begin{array}{ll} {(x+9)^2}&{(y−7)^2}\\ {(x+9)(x+9)}&{(y−7)(y−7)}\\ {x^2+9x+9x+81}&{y^2−7y−7y+49}\\ {x^2+18x+81}&{y^2−14y+49}\\ \nonumber \end{array}\]
Se a, b são números reais,
\((a+b)^2=a^2+2ab+b^2\)
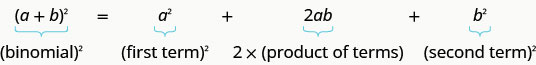
\((a−b)^2=a^2−2ab+b^2\)
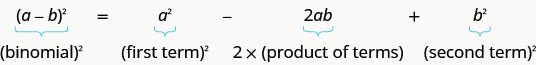
Podemos usar esse padrão para “fazer” um quadrado perfeito.
Começaremos com a expressão\(x^2+6x\). Como há um sinal de mais entre os dois termos, usaremos o\((a+b)^2\) padrão.
\(a^2+2ab+b^2=(a+b)^2\)
Observe que o primeiro termo de\(x^2+6x\) é um quadrado,\(x^2\).
Agora sabemos\(a=x\).
A que número podemos adicionar\(x^2+6x\) para criar um trinômio quadrado perfeito?
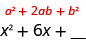
O termo médio do Padrão de Quadrados Binomiais, 2ab, é o dobro do produto dos dois termos do binômio. Isso significa o dobro do produto de x e algum número é 6x. Então, duas vezes algum número deve ser seis. O número que precisamos é\(\frac{1}{2}·6=3\). O segundo termo no binômio, b, deve ser 3.
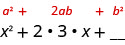
Agora sabemos\(b=3\).
Agora, apenas quadramos o segundo termo do binômio para obter o último termo do trinômio quadrado perfeito, então quadramos três para obter o último termo, nove.
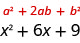
Agora podemos levar em consideração
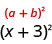
Então, descobrimos que adicionar nove para\(x^2+6x\) “completar o quadrado” e escrevemos como\((x+3)^2\).
Para completar o quadrado de\(x^2+bx\):
- Identifique b, o coeficiente de x.
- Encontre\((\frac{1}{2}b)^2\) o número para completar o quadrado.
- Adicione\( (\frac{1}{2}b)^2\) o\(x^2+bx\) a.
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um quadrado binomial.
\(x^2+14x\)
- Resposta
-
O coeficiente de x é 14. 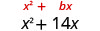
Encontre\((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅14)^2\)
\((7)^2\)
49
Adicione 49 ao binômio para completar o quadrado. \(x^2+14x+49\) Reescreva como um quadrado binomial. \((x+7)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(y^2+12y\)
- Resposta
-
\((y+6)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(z^2+8z\)
- Resposta
-
\((z+4)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado. \(m^2−26m\)
- Resposta
-
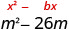
Encontre\((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅(−26))^2\)
\((−13)^2\)
169
Adicione 169 ao binômio para completar o quadrado. \(m^2−26m+169\) Reescreva como um quadrado binomial. \((m−13)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(a^2−20a\)
- Resposta
-
\((a−10)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(b^2−4b\)
- Resposta
-
\((b−2)^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado.
\(u^2−9u\)
- Resposta
-
O coeficiente de u é −9. 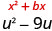
Encontre\((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅(−9))^2\)
\((−\frac{9}{2})^2\)
\(\frac{81}{4}\)
Adicione\(\frac{81}{4}\) ao binômio para completar o quadrado. \(u^2−9u+\frac{81}{4}\) Reescreva como um quadrado binomial. \((u−\frac{9}{2})^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(m^2−5m\)
- Resposta
-
\((m−\frac{5}{2})^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(n^2+13n\)
- Resposta
-
\((n+\frac{13}{2})^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Em seguida, escreva o resultado como um binômio quadrado.
\(p^2+12p\)
- Resposta
-
O coeficiente de p é\(\frac{1}{2}\) 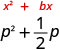
Encontre\((\frac{1}{2}b)^2\).
\((\frac{1}{2}⋅\frac{1}{2})^2\)
\((\frac{1}{4})^2\)
\(\frac{1}{16}\)
Adicione\(\frac{1}{16}\) ao binômio para completar o quadrado. \(p^2+\frac{1}{2}p+\frac{1}{16}\) Reescreva como um quadrado binomial. \((p+\frac{1}{4})^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(p^2+\frac{1}{4}p\)
- Resposta
-
\((p+\frac{1}{8})^2\)
Complete o quadrado para criar um trinômio quadrado perfeito. Escreva o resultado como um quadrado binomial.
\(q^2−\frac{2}{3}q\)
- Resposta
-
\((q−\frac{1}{3})^2\)
Resolva equações quadráticas da forma\(x^2 + bx + c = 0\) completando o quadrado
Ao resolver equações, devemos sempre fazer a mesma coisa nos dois lados da equação. Isso é verdade, é claro, quando resolvemos uma equação quadrática completando o quadrado também. Quando adicionamos um termo a um lado da equação para criar um trinômio quadrado perfeito, também devemos adicionar o mesmo termo ao outro lado da equação.
Por exemplo, se começarmos com a equação\(x^2+6x=40\) e quisermos completar o quadrado à esquerda, adicionaremos nove aos dois lados da equação.
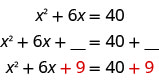
Em seguida, consideramos à esquerda e simplificamos à direita.
\((x+3)^2=49\)
Agora, a equação está na forma de resolver usando a propriedade de raiz quadrada. Completar o quadrado é uma forma de transformar uma equação na forma que precisamos para usar a propriedade de raiz quadrada.
Como resolver uma equação quadrática do formulário\(x^2+bx+c=0\) completando o quadrado.
Resolva\(x^2+8x=48\) completando o quadrado.
- Resposta
-


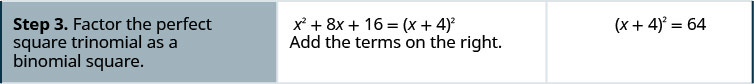



Resolva\(c^2+4c=5\) completando o quadrado.
- Resposta
-
\(c=−5\),\(c=1\)
Resolva\(d^2+10d=−9\) completando o quadrado.
- Resposta
-
\(d=−9\),\(d=−1\)
- Isole os termos variáveis em um lado e os termos constantes no outro.
- Encontre\((\frac{1}{2}·b)^2\) o número para completar o quadrado. Adicione-o aos dois lados da equação.
- Considere o trinômio quadrado perfeito como um quadrado binomial.
- Use a propriedade Square Root.
- Simplifique o radical e resolva as duas equações resultantes.
- Verifique as soluções.
Resolva\(y^2−6y=16\) completando o quadrado.
- Resposta
-
Os termos das variáveis estão no lado esquerdo. 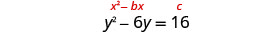
Pegue metade de −6 e enquadre-a. \((\frac{1}{2}(−6))^2=9\)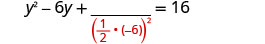
Adicione 9 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 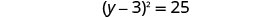
Use a propriedade Square Root. 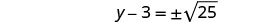
Simplifique o radical. 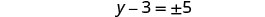
Resolva para y. 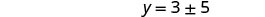
Reescreva para mostrar duas soluções. 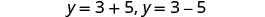
Resolva as equações. 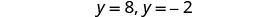
Verifique.
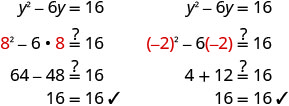
Resolva\(r^2−4r=12\) completando o quadrado.
- Responda
-
\(r=−2\),\(r=6\)
Resolver\(t^2−10t=11\) by completing the square.
- Responda
-
\(t=−1\),\(t=11\)
Resolva\(x^2+4x=−21\) completando o quadrado.
- Responda
-
Os termos das variáveis estão no lado esquerdo. 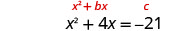
Pegue metade de 4 e enquadre-a. \((\frac{1}{2}(4))^2=4\)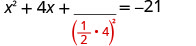
Adicione 4 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 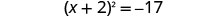
Use a propriedade Square Root. 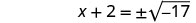
Não podemos pegar a raiz quadrada de um número negativo. Não existe uma solução real.
Resolva\(y^2−10y=−35\) completando o quadrado.
- Responda
-
nenhuma solução real
Resolva\(z^2+8z=−19\) completando o quadrado.
- Responda
-
nenhuma solução real
No exemplo anterior, não havia uma solução real porque\((x+k)^2\) was equal to a negative number.
Resolva\(p^2−18p=−6\) completando o quadrado.
- Responda
-
Os termos das variáveis estão no lado esquerdo. 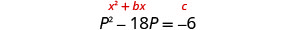
Pegue metade de −18 e enquadre-a. \((\frac{1}{2}(−18))^2=81\) 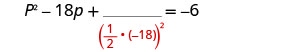
Adicione 81 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 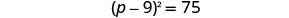
Use a propriedade Square Root. 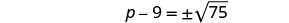
Simplifique o radical. 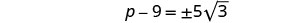
Resolva para p. 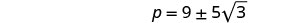
Reescreva para mostrar duas soluções. 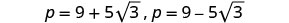
Verifique.
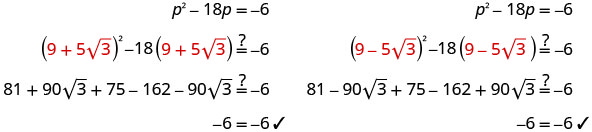
Outra forma de verificar isso seria usar uma calculadora. Avalie\(p^2−18p\) as duas soluções. A resposta deve ser −6.
Resolva\(x^2−16x=−16\) completando o quadrado.
- Responda
-
\(x=8\pm4\sqrt{3}\)
Resolva\(y^2+8y=11\) completando o quadrado.
- Responda
-
\(y=−4\pm3\sqrt{3}\)
Começaremos o próximo exemplo isolando os termos variáveis no lado esquerdo da equação.
Resolva\(x^2+10x+4=15\) completando o quadrado.
- Responda
-
Os termos das variáveis estão no lado esquerdo. 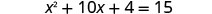
Subtraia 4 para obter os termos constantes no lado direito. 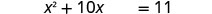
Pegue a metade de 10 e enquadre-a. \((\frac{1}{2}(10))^2=25\)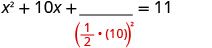
Adicione 25 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 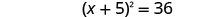
Use a propriedade Square Root. 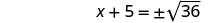
Simplifique o radical. 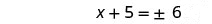
Resolva para x. 
Reescreva para mostrar duas equações. 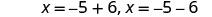
Resolva as equações. 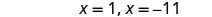
Verifique.
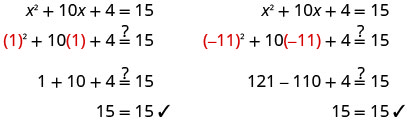
Resolva\(a^2+4a+9=30\) completando o quadrado.
- Responda
-
\(a=−7\),\(a=3\)
Resolver\(b^2+8b−4=16\) by completing the square.
- Responda
-
\(b=−10\),\(b=2\)
Para resolver a próxima equação, precisamos primeiro coletar todos os termos variáveis no lado esquerdo da equação. Em seguida, procedemos da mesma forma que fizemos nos exemplos anteriores.
Resolva\(n^2=3n+11\) completando o quadrado.
- Responda
-
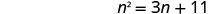
Subtraia 3 n para obter os termos variáveis no lado esquerdo. 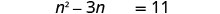
Pegue a metade de −3 e enquadre-a. \((\frac{1}{2}(−3))^2= \frac{9}{4}\) 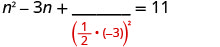
Adicione\(\frac{9}{4}\) aos dois lados. 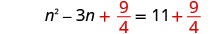
Considere o trinômio quadrado perfeito como um quadrado binomial. 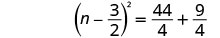
Adicione as frações no lado direito. 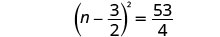
Use a propriedade Square Root. 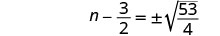
Simplifique o radical. 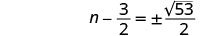
Resolva para n. 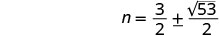
Reescreva para mostrar duas equações. 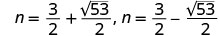
Verifique. Deixamos o cheque para você!
Resolva\(p^2=5p+9\) completando o quadrado.
- Responda
-
\(p=\frac{5}{2}\pm\frac{\sqrt{61}}{2}\)
Resolver\(q^2=7q−3\) by completing the square.
- Responda
-
\(q=\frac{7}{2}\pm\frac{\sqrt{37}}{2}\)
Observe que o lado esquerdo da próxima equação está na forma fatorada. Mas o lado direito não é zero, então não podemos usar a Propriedade do Produto Zero. Em vez disso, multiplicamos os fatores e, em seguida, colocamos a equação na forma padrão para resolver completando o quadrado.
Resolva\((x−3)(x+5)=9\) completando o quadrado.
- Responda
-
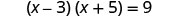
Multiplicamos binômios à esquerda. 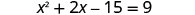
Adicione 15 para obter os termos variáveis no lado esquerdo. 
Pegue metade de 2 e enquadre-a. \((\frac{1}{2}(2))^2=1\)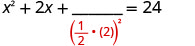
Adicione 1 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 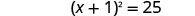
Use a propriedade Square Root. 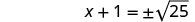
Resolva para x. 
Reescreva para mostrar duas soluções. 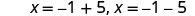
Simplifique. 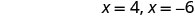
Verifique. Deixamos o cheque para você!
Resolva\((c−2)(c+8)=7\) completando o quadrado.
- Responda
-
\(c=−3\pm4\sqrt{2}\)
Resolva\((d−7)(d+3)=56\) completando o quadrado.
- Responda
-
\(d=−7\),\(d=11\)
Resolva equações quadráticas do formulário\( ax^2 + bx + c = 0\) completando o quadrado
O processo de completar o quadrado funciona melhor quando o coeficiente principal é um, então o lado esquerdo da equação é da forma\(x^2+bx+c\). Se o\(x^2\) termo tiver um coeficiente, tomamos algumas medidas preliminares para tornar o coeficiente igual a um.
Às vezes, o coeficiente pode ser calculado a partir de todos os três termos do trinômio. Essa será nossa estratégia no próximo exemplo.
Resolva\(3x^2−12x−15=0\) completando o quadrado.
- Responda
-
Para completar o quadrado, precisamos que o coeficiente\(x^2\) de seja um. Se considerarmos o coeficiente de\(x^2\) como um fator comum, podemos continuar resolvendo a equação completando o quadrado.
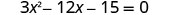
Considere o maior fator comum. 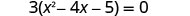
Divida os dois lados por 3 para isolar o trinômio. 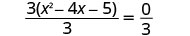
Simplifique. 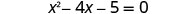
Subtraia 5 para obter os termos constantes à direita. 
Pegue metade de 4 e enquadre-a. \((\frac{1}{2}(4))^2=4\)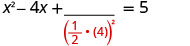
Adicione 4 aos dois lados. 
Considere o trinômio quadrado perfeito como um quadrado binomial. 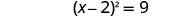
Use a propriedade Square Root. 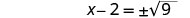
Resolva para x. 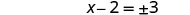
Reescreva para mostrar 2 soluções. 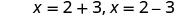
Simplifique. 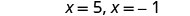
Verifique.
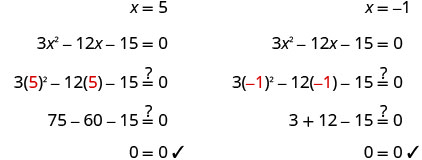
Resolva\(2m^2+16m−8=0\) completando o quadrado.
- Responda
-
\(m=−4\pm2\sqrt{5}\)
Resolva\(4n^2−24n−56=8\) completando o quadrado.
- Responda
-
\(n=−2, 8\)
Para completar o quadrado, o coeficiente principal deve ser um. Quando o coeficiente principal não for um fator de todos os termos, dividiremos os dois lados da equação pelo coeficiente principal. Isso nos dará uma fração para o segundo coeficiente. Já vimos como completar o quadrado com frações nesta seção.
Resolva\(2x^2−3x=20\) completando o quadrado.
- Responda
-
Novamente, nosso primeiro passo será fazer com que o coeficiente\(x^2\) seja um. Ao dividir os dois lados da equação pelo coeficiente de\(x^2\), podemos então continuar resolvendo a equação completando o quadrado.
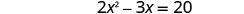
Divida os dois lados por 2 para obter o coeficiente de\(x^2\) 1. 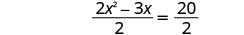
Simplifique. 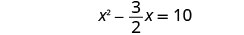
Pegue a metade\(−\frac{3}{2}\) e enquadre-a. \((\frac{1}{2}(−\frac{3}{2}))^2=\frac{9}{16}\)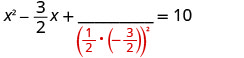
Adicione\(\frac{9}{16}\) aos dois lados. 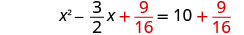
Considere o trinômio quadrado perfeito como um quadrado binomial. 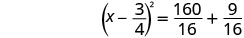
Adicione as frações no lado direito. 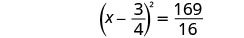
Use a propriedade Square Root. 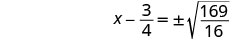
Simplifique o radical. 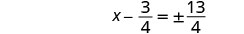
Resolva para x. 
Reescreva para mostrar 2 soluções. 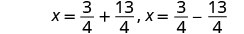
Simplifique. 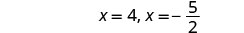
Verifique. Deixamos o cheque para você.
Resolva\(3r^2−2r=21\) completando o quadrado.
- Responda
-
\(r=−\frac{7}{3}\),\(r=3\)
Resolva\(4t^2+2t=20\) completando o quadrado.
- Responda
-
\(t=−\frac{5}{2}\),\(t=2\)
Resolva\(3x^2+2x=4\) completando o quadrado.
- Responda
-
Novamente, nosso primeiro passo será fazer com que o coeficiente\(x^2\) seja um. Ao dividir os dois lados da equação pelo coeficiente de\(x^2\), podemos então continuar resolvendo a equação completando o quadrado.
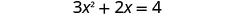
Divida os dois lados por 3 para que o coeficiente\(x^2\) seja igual a 1. 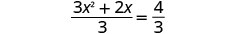
Simplifique. 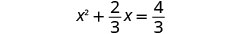
Pegue a metade\(\frac{2}{3}\) e enquadre-a. \((\frac{1}{2}⋅\frac{2}{3})^2=\frac{1}{9}\)
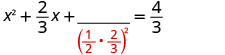
Adicione\(\frac{1}{9}\) aos dois lados. 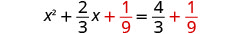
Considere o trinômio quadrado perfeito como um quadrado binomial. 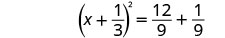
Use a propriedade Square Root. 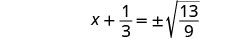
Simplifique o radical. 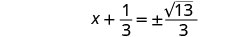
Resolva para x. 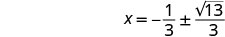
Reescreva para mostrar 2 soluções. 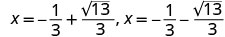
Verifique. Deixamos o cheque para você.
Resolva\(4x^2+3x=12\) completando o quadrado.
- Responda
-
\(x=−\frac{3}{8}\pm\frac{\sqrt{201}}{8}\)
Resolva\(5y^2+3y=10\) completando o quadrado.
- Responda
-
\(y=−\frac{3}{10}\pm\frac{\sqrt{209}}{10}\)
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de equações quadráticas completando o quadrado:
- Introdução ao método de preenchimento do quadrado
- Como resolver completando o quadrado
Conceitos-chave
- Padrão de quadrados binomiais Se a, ba, b são números reais,
\((a+b)^2=a^2+2ab+b^2\)
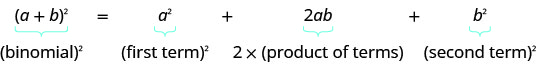
\((a−b)^2=a^2−2ab+b^2\)
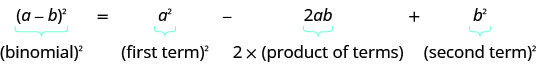
- Complete um quadrado
Para completar o quadrado de\(x^2+bx\):- Identifique bb, o coeficiente de x.
- Encontre\((\frac{1}{2}b)^2\) o número para completar o quadrado.
- Adicione\((\frac{1}{2}b)^2\) o\(x^2+bx\) a.
Glossário
- completando o quadrado
- Completar o quadrado é um método usado para resolver equações quadráticas.


