Skip to main content
Global

9.7: Raízes superiores

  1. Last updated
  2. Save as PDF
  • Page ID
    184083

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Simplifique expressões com raízes mais altas
    • Use a propriedade do produto para simplificar expressões com raízes mais altas
    • Use a propriedade do quociente para simplificar expressões com raízes mais altas
    • Adicione e subtraia raízes mais altas
    Nota
    1. Simplifique:\(y^{5}y^{4}\).
      Se você perdeu esse problema, consulte o Exemplo 6.2.7.
    2. Simplifique:\((n^2)^6\).
      Se você perdeu esse problema, consulte o Exemplo 6.2.19.
    3. Simplifique:\(\frac{x^8}{x^3}\).
      Se você perdeu esse problema, consulte o Exemplo 6.5.1.

    Simplifique expressões com raízes mais altas

    Até agora, neste capítulo, trabalhamos com quadrados e raízes quadradas. Agora estenderemos nosso trabalho para incluir poderes superiores e raízes superiores.

    Vamos revisar um pouco do vocabulário primeiro.

    \[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]

    Os termos “quadrado” e “cubo” vêm das fórmulas para a área de um quadrado e o volume de um cubo.

    Será útil ter uma tabela das potências dos números inteiros de −5 a 5. Veja a Figura\(\PageIdnex{1}\).

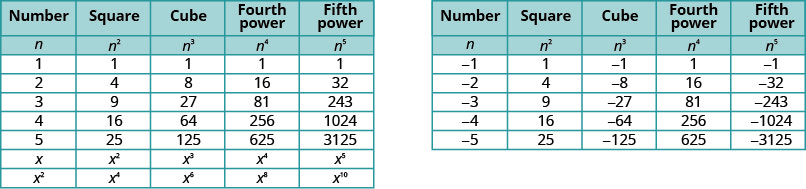
    Essa figura consiste em duas tabelas. A primeira tabela mostra os resultados do aumento dos números 1, 2, 3, 4, 5, x e x ao quadrado para a segunda, terceira, quarta e quinta potências. A segunda tabela mostra os resultados do aumento dos números de menos um a menos cinco para a segunda, terceira, quarta e quinta potências. A primeira tabela tem cinco colunas e nove linhas. O segundo tem cinco colunas e sete linhas. As colunas em ambas as tabelas são rotuladas como “Número”, “Quadrado”, “Cubo”, “Quarta potência”, “Quinta potência”, nada, “Número”, “Quadrado”, “Cubo”, “Quarta potência” e “Quinta potência”. Nas duas tabelas, a próxima linha diz: n, n ao quadrado, n ao cubo, n à quarta potência, n à quinta potência, nada, n, n ao quadrado, n ao cubo, n à quarta potência e n à quinta potência. Na primeira tabela, 1 quadrado, 1 cubo, 1 elevado à quarta potência e 1 elevado à quinta potência são mostrados como sendo 1. Na próxima linha, 2 ao quadrado é 4, 2 ao cubo é 8, 2 elevado à quarta potência é 16 e 2 elevado à quinta potência é 32. Na próxima linha, 3 ao quadrado é 9, 3 ao cubo é 27, 3 elevado à quarta potência é 81 e 3 elevado à quinta potência é 243. Na próxima linha, 4 ao quadrado é 16, 4 ao cubo é 64, 4 elevado à quarta potência é 246 e 4 elevado à quinta potência é 1024. Na próxima linha, 5 ao quadrado é 25, 5 ao cubo é 125, 5 elevado à quarta potência é 625 e 5 elevado à quinta potência é 3125. Na próxima linha, x ao quadrado, x ao cubo, x elevado à quarta potência e x à quinta potência são listados. Na próxima linha, x quadrado é x elevado à quarta potência, x ao quadrado é x elevado à quinta potência, x ao quadrado à quarta potência é x elevado à oitava potência e x quadrado à quinta potência é x elevado à décima potência. Na segunda tabela, menos 1 ao quadrado é 1, menos 1 ao cubo é menos 1, menos 1 elevado à quarta potência é 1 e menos 1 elevado à quinta potência é menos 1. Na próxima linha, menos 2 ao quadrado é 4, menos 2 ao cubo é menos 8, menos 2 elevado à quarta potência é 16 e menos 2 elevado à quinta potência é menos 32. Na próxima linha, menos 4 ao quadrado é 16, menos 4 ao cubo é menos 64, menos 4 elevado à quarta potência é 256 e menos 4 elevado à quinta potência é menos 1024. Na próxima linha, menos 5 ao quadrado é 25, menos 5 ao cubo é menos 125, menos 5 elevado à quarta potência é 625 e menos 5 elevado à quinta potência é menos 3125.
    Figura\(\PageIndex{1}\): Da primeira à quinta potências de números inteiros de −5 a 5.

    Observe os sinais na Figura\(\PageIndex{1}\). Todos os poderes dos números positivos são positivos, é claro. Mas quando temos um número negativo, as potências pares são positivas e as potências ímpares são negativas. Copiaremos a linha com as potências de −2 abaixo para ajudar você a ver isso.

    Essa figura tem cinco colunas e duas linhas. A primeira linha rotula cada coluna: n, n ao quadrado, n ao cubo, n elevado à quarta potência e n ao quinto poder. A segunda linha diz: menos 2, 4, menos 8, 16 e menos 32.

    No início deste capítulo, definimos a raiz quadrada de um número.

    Se\(n^2=m\), então n é uma raiz quadrada de m.

    E usamos a notação\(\sqrt{m}\) para denotar a raiz quadrada principal. Então,\(\sqrt{m} \ge 0\) sempre.

    Agora estenderemos a definição para raízes mais altas.

    Definição: NA RAIZ DE UM NÚMERO

    Se\(b^n=a\), então b é e n na raiz de um número a.

    O principal na raiz de um está escrito\(\sqrt[n]{a}=b\)

    n é chamado de índice do radical.

    Não escrevemos o índice para uma raiz quadrada. Assim como usamos a palavra “cubo” para\(b^3\), usamos o termo “raiz cúbica” para\(\sqrt[3]{a}\).

    Nós nos referimos à Figura\(\PageIndex{1}\) para nos ajudar a encontrar raízes mais altas.

    \[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]

    Poderíamos ter uma raiz par de um número negativo? Não. Sabemos que a raiz quadrada de um número negativo não é um número real. O mesmo vale para qualquer raiz uniforme. Mesmo as raízes dos números negativos não são números reais. As raízes ímpares dos números negativos são números reais.

    Definição: PROPRIEDADES DE\(\sqrt[n]{a}\)

    Quando n é um número par e

    • \(a\ge 0\), então\(\sqrt[n]{a}\) é um número real
    • \(a < 0\), então não\(\sqrt[n]{a}\) é um número real

    Quando n é um número ímpar,\(\sqrt[n]{a}\) é um número real para todos os valores de a.

    Exemplo\(\PageIndex{1}\)

    Simplifique:

    1. \(\sqrt[3]{8}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{32}\).
    Responda
    1. \(\sqrt[3]{8}\)
    Desde\((2)^3=8\). 2
    2. \(\sqrt[4]{81}\)
    Desde\((3)^4=81\). 3
    3. \(\sqrt[5]{32}\)
    Desde\((2)^5=32\). 2
    Exemplo\(\PageIndex{2}\)

    Simplifique:

    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{243}\).
    Responda
    1. 3
    2. 4
    3. 3
    Exemplo\(\PageIndex{3}\)

    Simplifique:

    1. \(\sqrt[3]{1000}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{32}\).
    Responda
    1. 10
    2. 2
    3. 2
    Exemplo\(\PageIndex{4}\)

    Simplifique:

    1. \(\sqrt[3]{−64}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−243}\).
    Responda
    1. \(\sqrt[3]{−64}\)
    Desde\((−4)^3=−64\). −4
    2. \(\sqrt[4]{−16}\)
    Pense,\((?)^4=−16\) .Nenhum número real elevado à quarta potência é positivo. Não é um número real.
    3. \(\sqrt[5]{−243}\)
    Desde\((−3)^5=−243\). −3
    Exemplo\(\PageIndex{5}\)

    Simplifique:

    1. \(\sqrt[3]{−125}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−32}\).
    Responda
    1. −5
    2. não é real
    3. −2
    Exemplo\(\PageIndex{6}\)

    Simplifique:

    1. \(\sqrt[3]{−216}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−1024}\).
    Responda
    1. −6
    2. não é real
    3. −4
    Quando trabalhamos com raízes quadradas que tinham variáveis no radicando, restringimos as variáveis a valores não negativos. Agora, removeremos essa restrição.

    A raiz ímpar de um número pode ser positiva ou negativa. Nós vimos isso\(\sqrt[3]{−64}=−4\).

    Mas a raiz par de um número não negativo é sempre não negativa, porque tomamos o principal n na raiz.

    Suponha que comecemos com a=−5.

    \[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]

    Como podemos garantir que a quarta raiz de −5, elevada à quarta potência,\((−5)^4\) seja 5? Veremos na propriedade a seguir.

    Definição: SIMPLIFICAR RAÍZES ÍMPARES E PARES

    Para qualquer número inteiro\(n \ge 2\),

    \[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]

    Devemos usar os sinais de valor absoluto quando tomamos uma raiz uniforme de uma expressão com uma variável no radical.

    Exemplo\(\PageIndex{7}\)

    Simplifique:

    1. \(\sqrt{x^2}\)
    2. \(\sqrt[3]{n^3}\)
    3. \(\sqrt[4]{p^4}\)
    4. \(\sqrt[5]{y^5}\).
    Responda

    Usamos o valor absoluto para ter certeza de obter a raiz positiva.

    1. \(\sqrt{x^2}\)
    Desde então\((x)^2=x^2\), queremos a raiz positiva. |x|
    2. \(\sqrt[3]{n^3}\)
    Desde\((n)^3=n^3\). É uma raiz ímpar, então não há necessidade de um sinal de valor absoluto. n
    3. \(\sqrt[4]{p^4}\)
    Desde então\((p)^4=p^4\), queremos a raiz positiva. |p|
    4. \(\sqrt[5]{y^5}\)
    Desde\((y)^5=y^5\). É uma raiz ímpar, então não há necessidade de um sinal de valor absoluto. y
    Exemplo\(\PageIndex{8}\)

    Simplifique:

    1. \(\sqrt{b^2}\)
    2. \(\sqrt[3]{w^3}\)
    3. \(\sqrt[4]{m^4}\)
    4. \(\sqrt[5]{q^5}\).
    Responda
    1. |b|
    2. w
    3. |m|
    4. q
    Exemplo\(\PageIndex{9}\)

    Simplifique:

    1. \(\sqrt{y^2}\)
    2. \(\sqrt[3]{p^3}\)
    3. \(\sqrt[4]{z^4}\)
    4. \(\sqrt[5]{q^5}\)
    Responda
    1. |y|
    2. p
    3. |z|
    4. q
    Exemplo\(\PageIndex{10}\)

    Simplifique:

    1. \(\sqrt[3]{y^{18}}\)
    2. \(\sqrt[4]{z^8}\).
    Responda
    1. \(\sqrt[3]{y^{18}}\)
    Desde\((y^6)^3=y^18\). \(\sqrt[3]{(y^6)^3}\)
      \(y^6\)
    2. \(\sqrt[4]{z^8}\)
    Desde\((z^2)^4=z^8\). \(\sqrt[4]{(z^2)^4}\)
    Como\(z^2\) é positivo, não precisamos de um sinal de valor absoluto. \(z^2\)
    Exemplo\(\PageIndex{11}\)

    Simplifique:

    1. \(\sqrt[4]{u^{12}}\)
    2. \(\sqrt[3]{v^{15}}\).
    Responda
    1. \(u^3\)
    2. \(v^5\)
    Exemplo\(\PageIndex{12}\)

    Simplifique:

    1. \(\sqrt[5]{c^{20}}\)
    2. \(\sqrt[6]{d^{24}}\).
    Responda
    1. \(c^4\)
    2. \(d^4\)
    Exemplo\(\PageIndex{13}\)

    Simplifique:

    1. \(\sqrt[3]{64p^6}\)
    2. \(\sqrt[4]{16q^{12}}\).
    Responda
    1. \(\sqrt[3]{64p^6}\)
    Reescreva\(64p^6\) como\((4p^2)^3\). \(\sqrt[3]{(4p^2)^3}\)
    Pegue a raiz cúbica. \(4p^2\)
    2. \(\sqrt[4]{16q^{12}}\)
    Reescreva o radicando como uma quarta potência. \(\sqrt[4]{(2q^3)^4}\)
    Pegue a quarta raiz. \(2|q^3|\)
    Exemplo\(\PageIndex{14}\)

    Simplifique:

    1. \(\sqrt[3]{27x^{27}}\)
    2. \(\sqrt[4]{81q^{28}}\).
    Responda
    1. \(3x^9\)
    2. \(3∣q^7∣\)
    Exemplo\(\PageIndex{15}\)

    Simplifique:

    1. \(\sqrt[3]{125p^9}\)
    2. \(\sqrt[5]{243q^{25}}\)
    Responda
    1. \(5p^3\)
    2. \(3q^5\)

    Use a propriedade Product para simplificar expressões com raízes mais altas

    Simplificaremos expressões com raízes mais altas da mesma forma que simplificamos expressões com raízes quadradas. E na raiz é considerado simplificado se não tiver fatores de\(m^n\).

    Definição: SIMPLIFICADO NA RAIZ

    \(\sqrt[n]{a}\)é considerado simplificado se a não tiver fatores de\(m^n\).

    Vamos generalizar a propriedade do produto de raízes quadradas para incluir qualquer raiz inteira\(n \ge 2\).

    Definição: PROPRIEDADE DO PRODUTO N THE ROOTS

    \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)e\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)

    quando\(\sqrt[n]{a}\) e\(\sqrt[n]{b}\) são números reais e para qualquer número inteiro\(n \ge 2\)

    Exemplo\(\PageIndex{16}\)

    Simplifique:

    1. \(\sqrt[3]{x^4}\)
    2. \(\sqrt[4]{x^7}\).
    Responda

    1.

    		 \(\sqrt[3]{x^4}\)
    Reescreva o radicand como um produto usando o maior fator de cubo perfeito. \(\sqrt[3]{x^3·x}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[3]{x^3}·\sqrt[3]{x}\)
    Simplifique. \(x\sqrt[3]{x}\)
    2. \(\sqrt[4]{x^7}\)
    Reescreva o radicand como um produto usando o quarto fator de potência perfeito. \(\sqrt[4]{x^4·x^3}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[4]{x^4}·\sqrt[4]{x^3}\)
    Simplifique. \(|x|\sqrt[4]{x^3}\)
    Exemplo\(\PageIndex{17}\)

    Simplifique:

    1. \(\sqrt[4]{y^6}\)
    2. \(\sqrt[3]{z^5}\).
    Responda
    1. \(|y∣\sqrt[4]{y^2}\)
    2. \(z\sqrt[3]{z^2}\)
    Exemplo\(\PageIndex{18}\)

    Simplifique:

    1. \(\sqrt[5]{p^8}\)
    2. \(\sqrt[6]{q^{13}}\).
    Responda
    1. \(p\sqrt[5]{p^3}\)
    2. \( q^2\sqrt[6]{q}\)
    Exemplo\(\PageIndex{19}\)

    Simplifique:

    1. \(\sqrt[3]{16}\)
    2. \(\sqrt[4]{243}\).
    Responda
    1. \(\sqrt[3]{16}\)
      \(\sqrt[3]{2^4}\)
    Reescreva o radicand como um produto usando o maior fator de cubo perfeito. \(\sqrt[3]{2^3·2}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[3]{2^3}·\sqrt[3]{2}\)
    Simplifique. \(2\sqrt[3]{2}\)
    2. \(\sqrt[4]{243}\)
      \(\sqrt[4]{3^5}\)
    Reescreva o radicand como um produto usando o quarto fator de potência perfeito. \(\sqrt[4]{3^4·3}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[4]{3^4}·\sqrt[4]{3}\)
    Simplifique. \(3\sqrt[4]{3}\)
    Exemplo\(\PageIndex{20}\)

    Simplifique:

    1. \(\sqrt[3]{81}\)
    2. \(\sqrt[4]{64}\).
    Responda
    1. \(3\sqrt[3]{3}\)
    2. \(2\sqrt[4]{4}\)
    Exemplo\(\PageIndex{21}\)

    Simplifique:

    1. \(\sqrt[3]{625}\)
    2. \(\sqrt[4]{729}\).
    Responda
    1. \(5\sqrt[3]{5}\)
    2. \(3\sqrt[4]{9}\)

    Não se esqueça de usar os sinais de valor absoluto ao obter uma raiz uniforme de uma expressão com uma variável no radical.

    Exemplo\(\PageIndex{22}\)

    Simplifique:

    1. \(\sqrt[3]{24x^7}\)
    2. \(\sqrt[4]{80y^{14}}\).
    Responda
    1. \(\sqrt[3]{24x^7}\)
    Reescreva o radicand como um produto usando fatores de cubo perfeitos. \(\sqrt[3]{2^{3}x^{6}·3x}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\)
    Reescreva o primeiro radicando como\((2x^2)^3\) \(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\)
    Simplifique. \(2x^2\sqrt[3]{3x}\)
    2. \(\sqrt[4]{80y^{14}}\)
    Reescreva o radicand como um produto usando um quarto fator de potência perfeito. \(\sqrt[4]{2^{4}y^{12}·5y^2}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\)
    Reescreva o primeiro radicando como\((2y^3)^4\) \(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\)
    Simplifique. \(2|y^3|\sqrt[4]{5y^2}\)
    Exemplo\(\PageIndex{23}\)

    Simplifique:

    1. \(\sqrt[3]{54p^[10}]\)
    2. \(\sqrt[4]{64q^{10}}\).
    Responda
    1. \(3p^3\sqrt[3]{2p}\)
    2. \(2q^2\sqrt[4]{4q^2}\)
    Exemplo\(\PageIndex{24}\)

    Simplifique:

    1. \(\sqrt[3]{128m^{11}}\)
    2. \(\sqrt[4]{162n^7}\).
    Responda
    1. \(4m^3\sqrt[3]{2m^2}\)
    2. \(3|n|\sqrt[4]{2n^3}\)
    Exemplo\(\PageIndex{25}\)

    Simplifique:

    1. \(\sqrt[3]{−27}\)
    2. \(\sqrt[4]{−16}\).
    Responda
    1. \(\sqrt[3]{−27}\)
    Reescreva o radicand como um produto usando fatores de cubo perfeitos. \(\sqrt[3]{(−3)^3}\)
    Pegue a raiz cúbica. −3
    2. \(\sqrt[4]{−16}\)
    Não existe um número real n onde\(n^4=−16\). Não é um número real.
    Exemplo\(\PageIndex{26}\)

    Simplifique:

    1. \(\sqrt[3]{−108}\)
    2. \(\sqrt[4]{−48}\).
    Responda
    1. \(−3\sqrt[3]{4}\)
    2. não é real
    Exemplo\(\PageIndex{27}\)

    Simplifique:

    1. \(\sqrt[3]{−625}\)
    2. \(\sqrt[4]{−324}\).
    Responda
    1. \(−5\sqrt[3]{5}\)
    2. não é real

    Use a propriedade quociente para simplificar expressões com raízes mais altas

    Podemos simplificar raízes mais altas com quocientes da mesma forma que simplificamos raízes quadradas. Primeiro, simplificamos todas as frações dentro do radical.

    Exemplo\(\PageIndex{28}\)

    Simplifique:

    1. \(\sqrt[3]{\frac{a^8}{a^5}}\)
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\).
    Responda

    1.

    		 \(\sqrt[3]{\frac{a^8}{a^5}}\)
    Simplifique primeiro a fração abaixo do radical. \(\sqrt[3]{a^3}\)
    Simplifique. uma
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\)
    Simplifique primeiro a fração abaixo do radical. \(\sqrt[4]{a^8}\)
    Reescreva o radicando usando fatores de quarta potência perfeitos. \(\sqrt[4]{(a^2)^4}\)
    Simplifique. \(a^2\)
    Exemplo\(\PageIndex{29}\)

    Simplifique:

    1. \(\sqrt[4]{\frac{x^7}{x^3}}\)
    2. \(\sqrt[4]{\frac{y^{17}}{y^5}}\).
    Responda
    1. |x|
    2. \(y^3\)
    Exemplo\(\PageIndex{30}\)

    Simplifique:

    1. \(\sqrt[3]{\frac{m^{13}}{m^7}}\)
    2. \(\sqrt[5]{\frac{n^{12}}{n^2}}\).
    Responda
    1. \(m^2\)
    2. \(n^2\)

    Anteriormente, usávamos a propriedade do quociente “ao contrário” para simplificar as raízes quadradas. Agora vamos generalizar a fórmula para incluir raízes mais altas.

    Definição: PROPRIEDADE DO QUOCIENTE DE N AS RAÍZES

    \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)e\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)

    quando\(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b \ne 0\), and for any integer \(n \ge 2\)

    Exercício\(\PageIndex{31}\)

    Simplifique:

    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Responda
    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    Nenhum dos radicandos é um cubo perfeito, então use a propriedade do quociente para escrever como um radical. \(\sqrt[3]{\frac{−108}{2}}\)
    Simplifique a fração abaixo do radical. \(\sqrt[3]{−54}\)
    Reescreva o radicand como um produto usando fatores de cubo perfeitos. \(\sqrt[3]{(−3)^3·2}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\)
    Simplifique. \(−3\sqrt[3]{2}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Nenhum dos radicandos é uma quarta potência perfeita, então use a propriedade do quociente para escrever como um radical \(\sqrt[4]{\frac{96x^7}{3x^2}}\)
    Simplifique a fração abaixo do radical. \(\sqrt[4]{32x^5}\)
    Reescreva o radicand como um produto usando um quarto fator de potência perfeito. \(\sqrt[4]{2^{4}x^4·2x}\)
    Reescreva o radical como produto de dois radicais. \(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\)
    Simplifique. \(2|x|\sqrt[4]{2x}\)
    Exemplo\(\PageIndex{32}\)

    Simplifique:

    1. \(\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}\)
    Responda
    1. não é real
    2. \(3|m|\sqrt[4]{2m^2}\)
    Exemplo\(\PageIndex{33}\)

    Simplifique:

    1. \(\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}\)
    2. \(\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}\).
    Responda
    1. −4
    2. \(3|n|\sqrt[4]{2}\)

    Se a fração dentro do radical não puder ser simplificada, usamos a primeira forma da propriedade do quociente para reescrever a expressão como o quociente de dois radicais.

    Exemplo\(\PageIndex{34}\)

    Simplifique:

    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\).
    Responda
    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    A fração no radicando não pode ser simplificada. Use a propriedade do quociente para escrever como dois radicais. \(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\)
    Reescreva cada radicando como um produto usando fatores de cubo perfeitos. \(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\)
    Reescreva o numerador como o produto de dois radicais. \(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\)
    Simplifique. \(\frac{2x^2\sqrt[3]{3x}}{y}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\)
    A fração no radicando não pode ser simplificada. Use a propriedade do quociente para escrever como dois radicais. \(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\)
    Reescreva cada radicando como um produto usando fatores de cubo perfeitos. \(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\)
    Reescreva o numerador como o produto de dois radicais. \(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\)
    Simplifique. \(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)
    Exemplo\(\PageIndex{35}\)

    Simplifique:

    1. \(\sqrt[3]{\frac{108c^{10}}{d^6}}\)
    2. \(\sqrt[4]{\frac{80x^{10}}{y^5}}\).
    Responda
    1. \(\frac{3c^3\sqrt[3]{4c}}{d^2}\)
    2. \(\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}\)
    Exemplo\(\PageIndex{36}\)

    Simplifique:

    1. \(\sqrt[3]{\frac{40r^3}{s}}\)
    2. \(\sqrt[4]{\frac{162m^{14}}{n^{12}}}\)
    Responda
    1. \(r\sqrt[3]{\frac{40}{s}}\)
    2. \(\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}\)

    Adicione e subtraia raízes superiores

    Podemos adicionar e subtrair raízes mais altas, como adicionamos e subtraímos raízes quadradas. Primeiro, fornecemos uma definição formal de radicais semelhantes.

    Definição: COMO RADICAIS

    Radicais com o mesmo índice e o mesmo radicando são chamados de radicais semelhantes.

    Radicais semelhantes têm o mesmo índice e o mesmo radicando.

    • \(9\sqrt[4]{42x}\)e\(−2\sqrt[4]{42x}\) são como radicais.
    • \(5\sqrt[3]{125x}\)e não\(6\sqrt[3]{125y}\) são como os radicais. Os radicandos são diferentes.
    • \(2\sqrt[5]{1000q}\)e não\(−4\sqrt[4]{1000q}\) são como os radicais. Os índices são diferentes.

    Somamos e subtraímos radicais semelhantes da mesma forma que adicionamos e subtraímos termos semelhantes. Podemos adicionar\(9\sqrt[4]{42x}+(−2\sqrt[4]{42x})\) e o resultado é\(7\sqrt[4]{42x}\).

    Exemplo\(\PageIndex{37}\)

    Simplifique:

    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Responda
    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    Os radicais são como, então adicionamos os coeficientes \(2\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Os radicais são semelhantes, então subtraímos os coeficientes. \(2\sqrt[4]{8}\)
    Exemplo\(\PageIndex{38}\)

    Simplifique:

    1. \(\sqrt[5]{3x}+\sqrt[5]{3x}\)
    2. \(3\sqrt[3]{9}−\sqrt[3]{9}\)
    Responda
    1. \(2\sqrt[5]{3x}\)
    2. \(2\sqrt[3]{9}\)
    Exemplo\(\PageIndex{39}\)

    Simplifique:

    1. \(\sqrt[4]{10y}+\sqrt[4]{10y}\)
    2. \(5\sqrt[6]{32}−3\sqrt[6]{32}\).
    Responda
    1. \(2\sqrt[4]{10y}\)
    2. \(2\sqrt[6]{32}\)

    Quando uma expressão não parece ter radicais semelhantes, vamos simplificar cada radical primeiro. Às vezes, isso leva a uma expressão com radicais semelhantes.

    Exemplo\(\PageIndex{40}\)

    Simplifique:

    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\).
    Responda
    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    Reescreva cada radicando usando fatores de cubo perfeitos. \(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\)
    Reescreva os cubos perfeitos. \(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\)
    Simplifique os radicais sempre que possível. \(3\sqrt[3]{2}−2\sqrt[3]{2}\)
    Combine como radicais. \(\sqrt[3]{2}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\)
    Reescreva usando um quarto fator de potência perfeito. \(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\)
    Reescreva cada radicando como um produto usando fatores de cubo perfeitos. \(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\)
    Reescreva o numerador como o produto de dois radicais. \(2\sqrt[4]{3}+3\sqrt[4]{3}\)
    Simplifique. \(5\sqrt[4]{3}\)
    Exemplo\(\PageIndex{41}\)

    Simplifique:

    1. \(\sqrt[3]{192}−\sqrt[3]{81}\)
    2. \(\sqrt[4]{32}+\sqrt[4]{512}\).
    Responda
    1. \(\sqrt[3]{3}\)
    2. \(6\sqrt[4]{2}\)
    Exemplo\(\PageIndex{42}\)

    Simplifique:

    1. \(\sqrt[3]{108}−\sqrt[3]{250}\)
    2. \(\sqrt[5]{64}+\sqrt[5]{486}\).
    Responda
    1. \(−\sqrt[3]{2}\)
    2. \(5\sqrt[5]{2}\)
    Exemplo\(\PageIndex{43}\)

    Simplifique:

    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{512y^5}\).
    Responda
    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    Reescreva cada radicando usando fatores de cubo perfeitos. \(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\)
    Reescreva os cubos perfeitos. \(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\)
    Simplifique os radicais sempre que possível. \(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\)
    Reescreva usando um quarto fator de potência perfeito. \(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\)
    Reescreva cada radicando como um produto usando fatores de cubo perfeitos. \(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\)
    Reescreva o numerador como o produto de dois radicais. \(3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}\)
    Exemplo\(\PageIndex{44}\)

    Simplifique:

    1. \(\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}\)
    2. \(\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}\).
    Responda
    1. \(2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}\)
    2. \(3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}\)
    Exemplo\(\PageIndex{45}\)

    Simplifique:

    1. \(\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}\)
    2. \(\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}\).
    Responda
    1. \(2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}\)
    2. \(2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}\)
    Acesse esses recursos on-line para obter instruções e práticas adicionais com a simplificação de raízes superiores.
    • Simplificando raízes superiores
    • Adicione/subtraia raízes com índices mais altos

    Conceitos-chave

    • Propriedades de
    • \(\sqrt[n]{a}\)quando n é um número par e
      • \(a \ge 0\), então\(\sqrt[n]{a}\) é um número real
      • \(a < 0\), então não\(\sqrt[n]{a}\) é um número real
      • Quando n é um número ímpar,\(\sqrt[n]{a}\) é um número real para todos os valores de a.
      • Para qualquer número inteiro\(n \ge 2\), quando n é ímpar\(\sqrt[n]{a^n}=a\)
      • Para qualquer número inteiro\(n \ge 2\), quando n é par\(\sqrt[n]{a^n}=|a|\)
    • \(\sqrt[n]{a}\)é considerado simplificado se a não tiver fatores de\(m^n\).
    • \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)e\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
    • \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)e\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
    • Para combinar como os radicais, basta adicionar ou subtrair os coeficientes, mantendo o radical igual.

    Glossário

    Na raiz de um número
    Se\(b^n=a\), então b é e n na raiz de a.
    Um princípio na raiz
    O principal na raiz de um está escrito\(\sqrt[n]{a}\).
    índice
    \(\sqrt[n]{a}\)n é chamado de índice do radical.
    como radicais
    Radicais com o mesmo índice e o mesmo radicando são chamados de radicais semelhantes.