Skip to main content
Global

6.6: Dividir polinômios

  1. Last updated
  2. Save as PDF
  • Page ID
    184363

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Divida um polinômio por um monômio
    • Divida um polinômio por um binômio
    Nota

    Antes de começar, faça este teste de prontidão.

    1. Adicionar:\(\dfrac{3}{d}+\dfrac{x}{d}\)
      Se você perdeu esse problema, revise o Exercício 1.7.1.
    2. Simplifique:\(\dfrac{30 x y^{3}}{5 x y}\)
      se você perdeu esse problema, revise o Exercício 6.5.37.
    3. Combine termos semelhantes:\(8 a^{2}+12 a+1+3 a^{2}-5 a+4\)
      se você perdeu esse problema, consulte o Exercício 1.3.37.

    Divida um polinômio por um monômio

    Na última seção, você aprendeu a dividir um monômio por um monômio. À medida que você continua desenvolvendo seu conhecimento sobre polinômios, o próximo procedimento é dividir um polinômio de dois ou mais termos por um monômio.

    O método que usaremos para dividir um polinômio por um monômio é baseado nas propriedades da adição de frações. Então, começaremos com um exemplo para revisar a adição de frações.

    \(\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}\)

    Agora faremos isso ao contrário para dividir uma única fração em frações separadas.

    Vamos declarar a propriedade de adição de frações aqui exatamente como você a aprendeu e ao contrário.

    ADIÇÃO DE FRAÇÕES

    Se a, b e c são números onde\(c\neq 0\), então

    \[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]

    Usamos a forma à esquerda para adicionar frações e usamos a forma à direita para dividir um polinômio por um monômio.

    \(\begin{array}{ll}{\text { For example, }} & {\dfrac{y+2}{5}} \\ {\text { can be written }} & {\dfrac{y}{5}+\dfrac{2}{5}}\end{array}\)

    Usamos essa forma de adição de frações para dividir polinômios por monômios.

    DIVISÃO DE UM POLINÔMIO POR UM MONÔMIO

    Para dividir um polinômio por um monômio, divida cada termo do polinômio pelo monômio.

    Exercício\(\PageIndex{1}\)

    Encontre o quociente:\(\dfrac{7 y^{2}+21}{7}\)

    Resposta

    \(\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}\)

    Exercício\(\PageIndex{2}\)

    Encontre o quociente:\(\dfrac{8 z^{2}+24}{4}\)

    Resposta

    \(2 z^{2}+6\)

    Exercício\(\PageIndex{3}\)

    Encontre o quociente:\(\dfrac{18 z^{2}-27}{9}\)

    Resposta

    \(2 z^{2}-3\)

    Lembre-se de que a divisão pode ser representada como uma fração. Quando você for solicitado a dividir um polinômio por um monômio e ele ainda não estiver na forma fracionária, escreva uma fração com o polinômio no numerador e o monômio no denominador.

    Exercício\(\PageIndex{4}\)

    Encontre o quociente:\(\left(18 x^{3}-36 x^{2}\right) \div 6 x\)

    Resposta

    \(\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}\)

    Exercício\(\PageIndex{5}\)

    Encontre o quociente:\(\left(27 b^{3}-33 b^{2}\right) \div 3 b\)

    Resposta

    \(9 b^{2}-11 b\)

    Exercício\(\PageIndex{6}\)

    Encontre o quociente:\(\left(25 y^{3}-55 y^{2}\right) \div 5 y\)

    Resposta

    \(5 y^{2}-11 y\)

    Quando dividimos por um negativo, devemos ter muito cuidado com os sinais.

    Exercício\(\PageIndex{7}\)

    Encontre o quociente:\(\dfrac{12 d^{2}-16 d}{-4}\)

    Resposta

    \(\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}\)

    Exercício\(\PageIndex{8}\)

    Encontre o quociente:\(\dfrac{25 y^{2}-15 y}{-5}\)

    Resposta

    \(-5 y^{2}+3 y\)

    Exercício\(\PageIndex{9}\)

    Encontre o quociente:\(\dfrac{42 b^{2}-18 b}{-6}\)

    Resposta

    \(-7 b^{2}+3 b\)

    Exercício\(\PageIndex{10}\)

    Encontre o quociente:\(\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\)

    Resposta

    \(\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}\)

    Exercício\(\PageIndex{11}\)

    Encontre o quociente:\(\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}\)

    Resposta

    \(15 d^{4}+6 d^{2}\)

    Exercício\(\PageIndex{12}\)

    Encontre o quociente:\(\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}\)

    Resposta

    \(36 p^{4}-8 p^{2}\)

    Exercício\(\PageIndex{13}\)

    Encontre o quociente:\(\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\)

    Resposta

    \(\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}\)

    Exercício\(\PageIndex{14}\)

    Encontre o quociente:\(\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)\)

    Resposta

    \(-4 a+2 b\)

    Exercício\(\PageIndex{15}\)

    Encontre o quociente:\(\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)\)

    Resposta

    \(8 a^{5} b+6 a^{3} b^{2}\)

    Exercício\(\PageIndex{13}\)

    Encontre o quociente:\(\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\)

    Resposta

    \(\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}\)

    Exercício\(\PageIndex{14}\)

    Encontre o quociente:\(\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}\)

    Resposta

    \(5 x y+3 y-2 y^{2}\)

    Exercício\(\PageIndex{15}\)

    Encontre o quociente:\(\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}\)

    Resposta

    \(5 a^{2}+2 a^{2} b-6 b^{2}\)

    Exercício\(\PageIndex{16}\)

    Encontre o quociente:\(\dfrac{10 x^{2}+5 x-20}{5 x}\)

    Resposta

    \(\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}\)

    Exercício\(\PageIndex{17}\)

    Encontre o quociente:\(\dfrac{18 c^{2}+6 c-9}{6 c}\)

    Resposta

    \(3 c+1-\dfrac{3}{2 c}\)

    Exercício\(\PageIndex{18}\)

    Encontre o quociente:\(\dfrac{10 d^{2}-5 d-2}{5 d}\)

    Resposta

    \(2 d-1-\dfrac{2}{5 d}\)

    Divida um polinômio por um binômio

    Para dividir um polinômio por um binômio, seguimos um procedimento muito semelhante à divisão longa de números. Então, vamos examinar cuidadosamente os passos que tomamos quando dividimos um número de 3 dígitos, 875, por um número de 2 dígitos, 25.

    Nós escrevemos a divisão longa 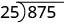A longa divisão de 875 por 25.
    Dividimos os dois primeiros dígitos, 87, por 25. 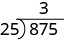25 cabe em 87 três vezes. 3 está escrito acima do segundo dígito de 875 no colchete de divisão longo.
    Multiplicamos 3 vezes 25 e escrevemos o produto abaixo de 87. 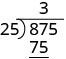O produto de 3 e 25 é 75, que está escrito abaixo dos dois primeiros dígitos de 875 no colchete de divisão longo.
    Agora subtraímos 75 de 87. 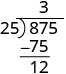87 menos 75 é 12, o que está escrito abaixo de 75.
    Em seguida, reduzimos o terceiro dígito do dividendo, 5. 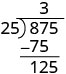O 5 em 875 é reduzido ao lado do 12, fazendo 125.
    Repita o processo, dividindo 25 em 125. 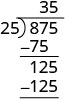25 cabe em 125 cinco vezes. 5 é escrito à direita do 3 no topo do colchete de divisão longo. 5 vezes 25 é 125. 125 menos 125 é zero. O restante é zero, então 25 cabe em 125 exatamente cinco vezes. 875 dividido por 25 é igual a 35.

    Verificamos a divisão multiplicando o quociente pelo divisor.

    Se fizermos a divisão corretamente, o produto deve ser igual ao dividendo.

    \[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]

    Agora vamos dividir um trinômio por um binômio. Ao ler o exemplo, observe como as etapas são semelhantes às do exemplo numérico acima.

    Exercício\(\PageIndex{19}\)

    Encontre o quociente:\(\left(x^{2}+9 x+20\right) \div(x+5)\)

    Resposta
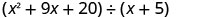
      Um trinômio, x ao quadrado mais 9 x mais 20, dividido por um binômio, x mais 5.
    Escreva isso como um problema de divisão longa.  
    Certifique-se de que o dividendo esteja no formato padrão. 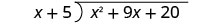A divisão longa de x ao quadrado mais 9 x mais 20 por x mais 5
    Divida x 2 por x. Pode ser útil perguntar a si mesmo: “Por que preciso multiplicar x para obter x 2?”  
    Coloque a resposta, x, no quociente sobre o termo x. 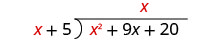x se encaixa em x ao quadrado x vezes. x está escrito acima do segundo termo de x ao quadrado mais 9 x mais 20 no colchete de divisão longo.
    Multiplique x vezes x + 5. Alinhe os termos similares sob o dividendo. 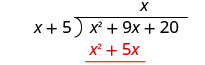O produto de x e x mais 5 é x ao quadrado mais 5 x, que está escrito abaixo dos dois primeiros termos de x ao quadrado mais 9x mais 20 no colchete de divisão longo.
    Subtraia x 2 + 5 x de x 2 + 9 x.  
    Você pode achar mais fácil alterar os sinais e depois adicionar.
    Em seguida, reduza o último mandato, 20.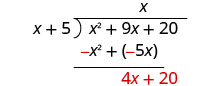    		 A soma de x ao quadrado mais 9 x e menos x ao quadrado mais menos 5 x é 4 x, que está escrito abaixo de menos 5 x. O terceiro termo em x ao quadrado mais 9 x mais 20 é reduzido ao lado de 4 x, resultando em 4 x mais 20.
    Divida 4 x por x. Pode ser útil perguntar a si mesmo: “Por que preciso
    multiplicar x para obter 4 x?”    		  
    Coloque a resposta, 4, no quociente sobre o termo constante. 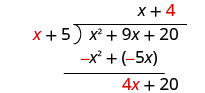4 x dividido por x é 4. Mais 4 está escrito em cima do colchete de divisão longo, ao lado de x e acima dos 20 em x ao quadrado mais 9 x mais 20.
    Multiplique 4 vezes x + 5. 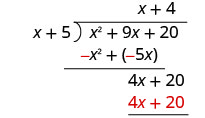x mais 5 vezes 4 é 4 x mais 20, que está escrito abaixo dos primeiros 4 x mais 20.
    Subtraia 4 x + 20 de 4 x + 20. 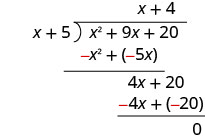4 x mais 20 menos 4 x mais 20 é 0. O restante é 0. x ao quadrado mais 9 x mais 20 dividido por x mais 5 é igual a x mais 4.
    Confira:  
    Multiplique o quociente pelo divisor.  
    (x + 4) (x + 5)  
    Você deve receber o dividendo.  
    x 2 + 9 x + 20 ✓
    Exercício\(\PageIndex{20}\)

    Encontre o quociente:\(\left(y^{2}+10 y+21\right) \div(y+3)\)

    Resposta

    y+7

    Exercício\(\PageIndex{21}\)

    Encontre o quociente:\(\left(m^{2}+9 m+20\right) \div(m+4)\)

    Resposta

    m+5

    Quando o divisor tem sinal de subtração, devemos ter muito cuidado ao multiplicar o quociente parcial e depois subtrair. Talvez seja mais seguro mostrar que alteramos os sinais e depois adicionamos.

    Exercício\(\PageIndex{22}\)

    Encontre o quociente:\(\left(2 x^{2}-5 x-3\right) \div(x-3)\)

    Resposta
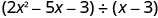
      Um trinômio, 2 x ao quadrado menos 5 x menos 3, dividido por um binômio, x menos 3.
    Escreva isso como um problema de divisão longa.  
    Certifique-se de que o dividendo esteja no formato padrão. 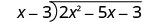A divisão longa de 2 x ao quadrado menos 5 x menos 3 por x menos 3.
    Divida 2 x 2 por x.
    Coloque a resposta, 2 x, no quociente sobre o termo x.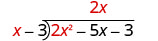    		 x cabe em 2 x ao quadrado 2 x vezes. 2 x está escrito acima do segundo termo de 2 x ao quadrado menos 5 x menos 3 no colchete de divisão longo.
    Multiplique 2 x vezes x − 3. Alinhe os termos similares sob o dividendo. 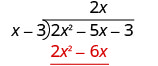O produto de 2 x e x menos 3 é 2 x ao quadrado menos 6 x, que está escrito abaixo dos dois primeiros termos de 2 x ao quadrado menos 5 x menos 3 no colchete de divisão longo.
    Subtraia 2 x 2 − 6 x de 2 x 2 − 5 x.
    Mude os sinais e, em seguida, adicione.
    Em seguida, reduza o último mandato.    		 A soma de 2 x ao quadrado menos 5 x e menos 2 x ao quadrado mais 6 x é x, que está escrito abaixo de 6 x. O terceiro termo em 2 x ao quadrado menos 5 x menos 3 é reduzido ao lado de x, tornando x menos 3.
    Divida x por x.
    Coloque a resposta, 1, no quociente sobre o termo constante.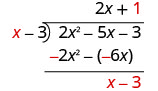    		 Mais 1 está escrito no topo do colchete de divisão longo, ao lado de 2 x e acima do menos 3 em 2 x ao quadrado menos 5 x menos 3.
    Multiplique 1 vezes x − 3. 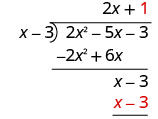x menos 3 vezes 1 é x menos 3, que está escrito abaixo do primeiro x menos 3.
    Subtraia x − 3 de x − 3 alterando os sinais e adicionando. 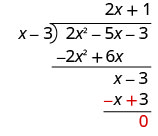O binômio x menos 3 menos o binômio negativo x mais 3 é 0. O restante é 0. 2 x ao quadrado menos 5 x menos 3 dividido por x menos 3 é igual a 2 x mais 1.
    Para verificar, multiplique (x − 3) (2 x + 1).  
    O resultado deve ser 2 x 2 − 5 x − 3.
    Exercício\(\PageIndex{23}\)

    Encontre o quociente:\(\left(2 x^{2}-3 x-20\right) \div(x-4)\)

    Resposta

    2x+5

    Exercício\(\PageIndex{24}\)

    Encontre o quociente:\(\left(3 x^{2}-16 x-12\right) \div(x-6)\)

    Resposta

    3x+2

    Quando dividimos 875 por 25, não tínhamos resto. Mas às vezes a divisão de números deixa um resto. O mesmo acontece quando dividimos polinômios. No Exercício\(\PageIndex{25}\), teremos uma divisão que deixa um restante. Escrevemos o restante como uma fração com o divisor como denominador.

    Exercício\(\PageIndex{25}\)

    Encontre o quociente:\(\left(x^{3}-x^{2}+x+4\right) \div(x+1)\)

    Resposta
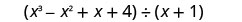
      Um polinômio, x ao cubo menos x ao quadrado mais x mais 4, dividido por outro polinômio, x mais 1.
    Escreva isso como um problema de divisão longa.  
    Certifique-se de que o dividendo esteja no formato padrão. 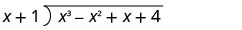A divisão longa de x ao cubo menos x ao quadrado mais x mais 4 por x mais 1.
    Divida x 3 por x.
    Coloque a resposta, x 2, no quociente sobre o termo x 2.
    Multiplique x 2 vezes x + 1. Alinhe os termos similares sob o dividendo.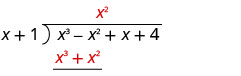    		 x se encaixa em x ao quadrado x vezes. x está escrito acima do segundo termo de x ao cubo menos x ao quadrado mais x mais 4 no colchete de divisão longo.
    Subtraia x 3 + x 2 de x 3 − x 2 alterando os sinais e adicionando.
    Em seguida, reduza o próximo semestre.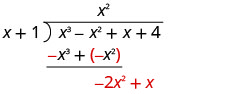    		 A soma de x ao cubo menos x ao quadrado e menos x ao cubo mais menos x ao quadrado é menos 2 x ao quadrado, que é escrito abaixo do x ao quadrado negativo. O próximo termo em x ao cubo menos x ao quadrado mais x mais 4 é reduzido ao lado de menos 2 x ao quadrado, tornando menos 2 x ao quadrado mais x.
    Divida −2 x 2 por x.
    Coloque a resposta, −2 x, no quociente sobre o termo x.
    Multiplique −2 x vezes x + 1. Alinhe os termos similares sob o dividendo.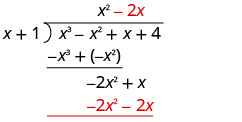    		 Menos 2 x está escrito em cima do colchete de divisão longo, ao lado de x ao quadrado e acima do x em x ao cubo menos x ao quadrado mais x mais 4. Menos 2 x ao quadrado menos 2 x está escrito abaixo de menos 2 x ao quadrado mais x.
    Subtraia −2 x 2 − 2 x de −2 x 2 + x alterando os sinais e adicionando.
    Em seguida, reduza o último mandato.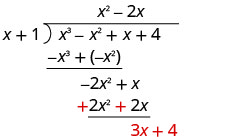    		 A soma de menos 2 x ao quadrado mais x e 2 x ao quadrado mais 2 x é considerada 3 x. O último termo em x ao cubo menos x ao quadrado mais x mais 4 é reduzido, resultando em 3 x mais 4.
    Divida 3 x por x.
    Coloque a resposta, 3, no quociente sobre o termo constante.
    Multiplique 3 vezes x + 1. Alinhe os termos similares sob o dividendo.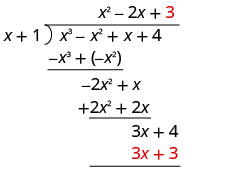    		 Mais 3 está escrito em cima do colchete de divisão longo, acima do 4 pol x ao cubo menos x ao quadrado mais x mais 4. 3 x mais 3 está escrito abaixo de 3 x mais 4.
    Subtraia 3 x + 3 de 3 x + 4 alterando os sinais e adicionando.
    Escreva o restante como uma fração com o divisor como denominador.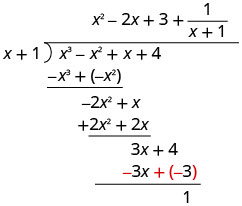    		 A soma de 3 x mais 4 e menos 3 x mais menos 3 é 1. Portanto, o polinômio x ao cubo menos x ao quadrado mais x mais 4, dividido pelo binômio x mais 1, é igual a x ao quadrado menos 2 x mais a fração 1 sobre x mais 1.
    Para verificar, multiplique\((x+1)\left(x^{2}-2 x+3+\dfrac{1}{x+1}\right)\)
    O resultado deve ser\(x^{3}-x^{2}+x+4\)
    Exercício\(\PageIndex{26}\)

    Encontre o quociente:\(\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)\)

    Resposta

    \(x^{2}+3 x+2+\dfrac{2}{x+2}\)

    Exercício\(\PageIndex{27}\)

    Encontre o quociente:\(\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)\)

    Resposta

    \(2 x^{2}+6 x-5-\dfrac{3}{x+1}\)

    Examine os dividendos em Exemplo, Exemplo e Exemplo. Os termos foram escritos em ordem decrescente de graus e não faltavam graus. O dividendo em Example será\(x^{4}-x^{2}+5 x-2\). Está faltando um\(x^{3}\) termo. Vamos adicionar\(0x^{3}\) como um espaço reservado.

    Exercício\(\PageIndex{28}\)

    Encontre o quociente:\(\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)\)

    Resposta

    Observe que não há\(x^{3}\) prazo no dividendo. Vamos adicionar\(0x^{3}\) como um espaço reservado.

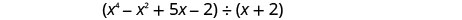
      Um polinômio, x elevado à quarta potência menos x ao quadrado menos 5 x menos 2, dividido por outro polinômio, x mais 2.
    Escreva isso como um problema de divisão longa. Certifique-se de que o dividendo esteja no formato padrão com espaços reservados para termos ausentes. 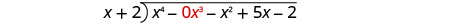A divisão longa de x até a quarta potência mais 0 x ao cubo menos x ao quadrado menos 5 x menos 2 por x mais 2.
    Divida x 4 por x.
    Coloque a resposta, x 3, no quociente sobre o termo x 3.
    Multiplique x 3 vezes x + 2. Alinhe os termos semelhantes.
    Subtraia e, em seguida, reduza o próximo termo.    		 x cubed é escrito em cima do colchete de divisão longo acima do termo x ao cubo no dividendo. Abaixo dos dois primeiros termos do dividendo x, a quarta potência mais 2 x ao cubo é subtraída para dar menos 2 x ao cubo menos x ao quadrado. Uma nota ao lado da divisão diz: “Pode ser útil mudar os sinais e acrescentar”.
    Divida −2 x 3 por x.
    Coloque a resposta, −2 x 2, no quociente sobre o termo x 2.
    Multiplique −2 x 2 vezes x + 1. Alinhe os termos semelhantes.
    Subtraia e reduza o próximo termo.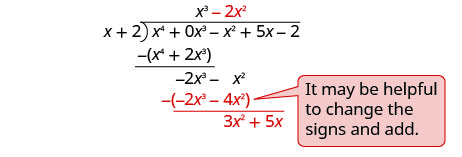    		 x ao cubo menos 2 x ao quadrado está escrito na parte superior do colchete de divisão longo. Na parte inferior da divisão longa, menos 2 x ao cubo menos 4 x ao quadrado são subtraídos para dar 3 x ao quadrado mais 5 x. Uma nota diz “Pode ser útil mudar os sinais e adicionar”.
    Divida 3 x 2 por x.
    Coloque a resposta, 3 x, no quociente sobre o termo x.
    Multiplique 3 x vezes x + 1. Alinhe os termos semelhantes.
    Subtraia e reduza o próximo termo.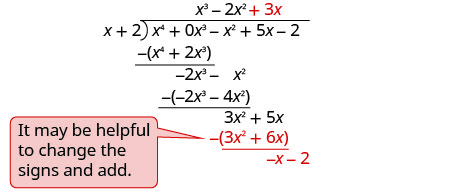    		 x ao cubo menos 2 x ao quadrado mais 3 x está escrito na parte superior do colchete de divisão longo. Na parte inferior da divisão longa, 3 x ao quadrado mais 6 x são subtraídos para dar menos x menos 2. Uma nota diz: “Pode ser útil mudar os sinais e acrescentar”.
    Divida − x por x.
    Coloque a resposta −1 no quociente sobre o termo constante.
    Multiplique −1 vezes x + 1. Alinhe os termos semelhantes.
    Mude os sinais, adicione.    		 x ao cubo menos 2 x ao quadrado mais 3 x menos 1 está escrito em cima do colchete de divisão longo. Na parte inferior da divisão longa, menos x menos 2 é subtraído para dar 0. Uma nota diz: “Pode ser útil mudar os sinais e acrescentar”. O polinômio x elevado à quarta potência menos x ao quadrado mais 5 x menos 2, dividido pelo binômio x mais 2 é igual ao polinômio x ao cubo menos 2 x ao quadrado mais 3 x menos 1.
    Para verificar, multiplique\((x+2)\left(x^{3}-2 x^{2}+3 x-1\right)\)  
    O resultado deve ser\(x^{4}-x^{2}+5 x-2\)
    Exercício\(\PageIndex{29}\)

    Encontre o quociente:\(\left(x^{3}+3 x+14\right) \div(x+2)\)

    Resposta

    \(x^{2}-2 x+7\)

    Exercício\(\PageIndex{30}\)

    Encontre o quociente:\(\left(x^{4}-3 x^{3}-1000\right) \div(x+5)\)

    Resposta

    \(x^{3}-8 x^{2}+40 x-200\)

    No Exercício\(\PageIndex{31}\), dividiremos por\(2a−3\). À medida que dividimos, teremos que considerar as constantes e as variáveis.

    Exercício\(\PageIndex{31}\)

    Encontre o quociente:\(\left(8 a^{3}+27\right) \div(2 a+3)\)

    Resposta

    Desta vez, mostraremos a divisão em uma única etapa. Precisamos adicionar dois espaços reservados para dividir.

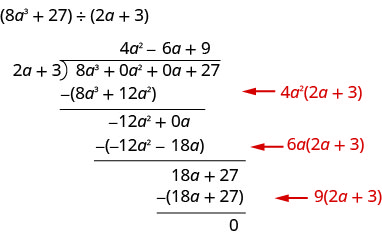
    A figura mostra a divisão longa de 8 ao cubo mais 27 por 2 a mais 3. No colchete de divisão longo, os espaços reservados 0 a ao quadrado e 0 a são adicionados ao polinômio. Na primeira linha abaixo do dividendo 8, subtrai-se um cubo mais 12 ao quadrado. À direita, uma seta indica que esse valor veio da multiplicação de 4 a ao quadrado por 2 a mais 3. A subtração dá menos 12 ao quadrado mais 0 a. Deste negativo 12, um quadrado menos 18 a é subtraído. À direita, uma seta indica que esse valor veio da multiplicação de 6 a por 2 a mais 3. A subtração dá 18 a mais 27. Deste 18, um mais 27 é subtraído. À direita, uma seta indica que esse valor veio da multiplicação de 9 por 2 a mais 3. O resultado é 0.

    Para verificar, multiplique\((2 a+3)\left(4 a^{2}-6 a+9\right)\)

    O resultado deve ser\(8 a^{3}+27\)

    Exercício\(\PageIndex{32}\)

    Encontre o quociente:\(\left(x^{3}-64\right) \div(x-4)\)

    Responda

    \(x^{2}+4 x+16\)

    Exercício\(\PageIndex{33}\)

    Encontre o quociente:\(\left(125 x^{3}-8\right) \div(5 x-2)\)

    Responda

    \(25 x^{2}+10 x+4\)

    Nota

    Acesse esses recursos on-line para obter instruções e práticas adicionais com a divisão de polinômios:

    • Divida um polinômio por um monômio
    • Divida um polinômio por um monômio 2
    • Divida o polinômio pelo binômio

    Conceitos-chave

    • Adição de frações
      • Se a, b e c são números onde\(c\neq 0\), então
        \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) e\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\)
    • Divisão de um polinômio por um monômio
      • Para dividir um polinômio por um monômio, divida cada termo do polinômio pelo monômio.