6.5E: Exercícios
- Page ID
- 184384
A prática leva à perfeição
Simplifique expressões usando a propriedade quociente para expoentes
Nos exercícios a seguir, simplifique.
- \(\dfrac{x^{18}}{x^{3}}\)
- \(\dfrac{5^{12}}{5^{3}}\)
- \(\dfrac{y^{20}}{y^{10}}\)
- \(\dfrac{7^{16}}{7^{2}}\)
- Responda
-
- \(y^{10}\)
- \(7^{14}\)
- \(\dfrac{p^{21}}{p^{7}}\)
- \(\dfrac{4^{16}}{4^{4}}\)
- \(\dfrac{u^{24}}{u^{3}}\)
- \(\dfrac{9^{15}}{9^{5}}\)
- Responda
-
- \(u^{21}\)
- \(9^{10}\)
- \(\dfrac{q^{18}}{q^{36}}\)
- \(\dfrac{10^{2}}{10^{3}}\)
- \(\dfrac{t^{10}}{t^{40}}\)
- \(\dfrac{8^{3}}{8^{5}}\)
- Responda
-
- \(\dfrac{1}{t^{30}}\)
- \(\dfrac{1}{64}\)
- \(\dfrac{b}{b^{9}}\)
- \(\dfrac{4}{4^{6}}\)
- \(\dfrac{x}{x^{7}}\)
- \(\dfrac{10}{10^{3}}\)
- Responda
-
- \(\dfrac{1}{x^{6}}\)
- \(\dfrac{1}{100}\)
Simplifique expressões com zero expoentes
Nos exercícios a seguir, simplifique.
- \(20^{0}\)
- \(b^{0}\)
- \(13^0\)
- \(k^{0}\)
- Responda
-
- 1
- 1
- \(-27^{0}\)
- \(-\left(27^{0}\right)\)
- \(-15^{0}\)
- \(-\left(15^{0}\right)\)
- Responda
-
- −1
- −1
- \((25 x)^{0}\)
- \(25 x^{0}\)
- \((6 y)^{0}\)
- \(6 y^{0}\)
- Responda
-
- 1
- 6
- \((12 x)^{0}\)
- \(\left(-56 p^{4} q^{3}\right)^{0}\)
- 7\(y^{0}(17 y)^{0}\)
- \(\left(-93 c^{7} d^{15}\right)^{0}\)
- Responda
-
- 7
- 1
- \(12 n^{0}-18 m^{0}\)
- \((12 n)^{0}-(18 m)^{0}\)
- \(15 r^{0}-22 s^{0}\)
- \((15 r)^{0}-(22 s)^{0}\)
- Responda
-
- −7
- 0
Simplifique expressões usando o quociente de uma propriedade de potência
Nos exercícios a seguir, simplifique.
- \(\left(\dfrac{3}{4}\right)^{3}\)
- \(\left(\dfrac{p}{2}\right)^{5}\)
- \(\left(\dfrac{x}{y}\right)^{6}\)
- \(\left(\dfrac{2}{5}\right)^{2}\)
- \(\left(\dfrac{x}{3}\right)^{4}\)
- \(\left(\dfrac{a}{b}\right)^{5}\)
- Responda
-
- \(\dfrac{4}{25}\)
- \(\dfrac{x^{4}}{81}\)
- \(\left(\dfrac{a}{b}\right)^{5}\)
- \(\left(\dfrac{a}{3 b}\right)^{4}\)
- \(\left(\dfrac{5}{4 m}\right)^{2}\)
- \(\left(\dfrac{a}{3 b}\right)^{4}\)
- \(\left(\dfrac{10}{3 q}\right)^{4}\)
- Responda
-
- \(\dfrac{x^{3}}{8 y^{3}}\)
- \(\dfrac{10,000}{81 q^{4}}\)
Simplifique as expressões aplicando várias propriedades
Nos exercícios a seguir, simplifique.
\(\dfrac{\left(a^{2}\right)^{3}}{a^{4}}\)
\(\dfrac{\left(p^{3}\right)^{4}}{p^{5}}\)
- Responda
-
\(p^{7}\)
\(\dfrac{\left(y^{3}\right)^{4}}{y^{10}}\)
\(\dfrac{\left(x^{4}\right)^{5}}{x^{15}}\)
- Responda
-
\(x^{5}\)
\(\dfrac{u^{6}}{\left(u^{3}\right)^{2}}\)
\(\dfrac{v^{20}}{\left(v^{4}\right)^{5}}\)
- Responda
-
1
\(\dfrac{m^{12}}{\left(m^{8}\right)^{3}}\)
\(\dfrac{n^{8}}{\left(n^{6}\right)^{4}}\)
- Resposta
-
\(\dfrac{1}{n^{16}}\)
\(\left(\dfrac{p^{9}}{p^{3}}\right)^{5}\)
\(\left(\dfrac{q^{8}}{q^{2}}\right)^{3}\)
- Resposta
-
\(q^{18}\)
\(\left(\dfrac{r^{2}}{r^{6}}\right)^{3}\)
\(\left(\dfrac{m^{4}}{m^{7}}\right)^{4}\)
- Resposta
-
\(\dfrac{1}{m^{12}}\)
\(\left(\dfrac{p}{r^{11}}\right)^{2}\)
\(\left(\dfrac{a}{b^{6}}\right)^{3}\)
- Resposta
-
\(\dfrac{a^{3}}{b^{18}}\)
\(\left(\dfrac{w^{5}}{x^{3}}\right)^{8}\)
\(\left(\dfrac{y^{4}}{z^{10}}\right)^{5}\)
- Resposta
-
\(\dfrac{y^{20}}{z^{50}}\)
\(\left(\dfrac{2 j^{3}}{3 k}\right)^{4}\)
\(\left(\dfrac{3 m^{5}}{5 n}\right)^{3}\)
- Resposta
-
\(\dfrac{27 m^{15}}{125 n^{3}}\)
\(\left(\dfrac{3 c^{2}}{4 d^{6}}\right)^{3}\)
\(\left(\dfrac{5 u^{7}}{2 v^{3}}\right)^{4}\)
- Resposta
-
\(\dfrac{625 u^{28}}{16 v^{12}}\)
\(\left(\dfrac{k^{2} k^{8}}{k^{3}}\right)^{2}\)
\(\left(\dfrac{j^{2} j^{5}}{j^{4}}\right)^{3}\)
- Resposta
-
\(j^{9}\)
\(\dfrac{\left(t^{2}\right)^{5}\left(t^{4}\right)^{2}}{\left(t^{3}\right)^{7}}\)
\(\dfrac{\left(q^{3}\right)^{6}\left(q^{2}\right)^{3}}{\left(q^{4}\right)^{8}}\)
- Resposta
-
\(\dfrac{1}{q^{8}}\)
\(\dfrac{\left(-2 p^{2}\right)^{4}\left(3 p^{4}\right)^{2}}{\left(-6 p^{3}\right)^{2}}\)
\(\dfrac{\left(-2 k^{3}\right)^{2}\left(6 k^{2}\right)^{4}}{\left(9 k^{4}\right)^{2}}\)
- Resposta
-
64\(k^{6}\)
\(\dfrac{\left(-4 m^{3}\right)^{2}\left(5 m^{4}\right)^{3}}{\left(-10 m^{6}\right)^{3}}\)
\(\dfrac{\left(-10 n^{2}\right)^{3}\left(4 n^{5}\right)^{2}}{\left(2 n^{8}\right)^{2}}\)
- Resposta
-
−4.000
Divida monômios
Nos exercícios a seguir, divida os monômios.
56\(b^{8} \div 7 b^{2}\)
63\(\nu^{10} \div 9 v^{2}\)
- Resposta
-
7\(v^{8}\)
\(-88 y^{15} \div 8 y^{3}\)
\(-72 u^{12} \div 12 u^{4}\)
- Resposta
-
\(-6 u^{8}\)
\(\dfrac{45 a^{6} b^{8}}{-15 a^{10} b^{2}}\)
\(\dfrac{54 x^{9} y^{3}}{-18 x^{6} y^{15}}\)
- Resposta
-
\(-\dfrac{3 x^{3}}{y^{12}}\)
\(\dfrac{15 r^{4} s^{9}}{18 r^{9} s^{2}}\)
\(\dfrac{20 m^{8} n^{4}}{30 m^{5} n^{9}}\)
- Resposta
-
\(\dfrac{-2 m^{3}}{3 n^{5}}\)
\(\dfrac{18 a^{4} b^{8}}{-27 a^{9} b^{5}}\)
\(\dfrac{45 x^{5} y^{9}}{-60 x^{8} y^{6}}\)
- Resposta
-
\(\dfrac{-3 y^{3}}{4 x^{3}}\)
\(\dfrac{64 q^{11} r^{9} s^{3}}{48 q^{6} r^{8} s^{5}}\)
\(\dfrac{65 a^{10} b^{8} c^{5}}{42 a^{7} b^{6} c^{8}}\)
- Resposta
-
\(\dfrac{65 a^{3} b^{2}}{42 c^{3}}\)
\(\dfrac{\left(10 m^{5} n^{4}\right)\left(5 m^{3} n^{6}\right)}{25 m^{7} n^{5}}\)
\(\dfrac{\left(-18 p^{4} q^{7}\right)\left(-6 p^{3} q^{8}\right)}{-36 p^{12} q^{10}}\)
- Resposta
-
\(\dfrac{-3 q^{5}}{p^{5}}\)
\(\dfrac{\left(6 a^{4} b^{3}\right)\left(4 a b^{5}\right)}{\left(12 a^{2} b\right)\left(a^{3} b\right)}\)
\(\dfrac{\left(4 u^{2} v^{5}\right)\left(15 u^{3} v\right)}{\left(12 u^{3} v\right)\left(u^{4} v\right)}\)
- Resposta
-
\(\dfrac{5 v^{4}}{u^{2}}\)
Prática m
- \(24 a^{5}+2 a^{5}\)
- \(24 a^{5}-2 a^{5}\)
- 24\(a^{5} \cdot 2 a^{5}\)
- 24\(a^{5} \div 2 a^{5}\)
- \(15 n^{10}+3 n^{10}\)
- \(15 n^{10}-3 n^{10}\)
- 15\(n^{10} \cdot 3 n^{10}\)
- 15\(n^{10} \div 3 n^{10}\)
- Resposta
-
- 18\(n^{10}\)
- 12\(n^{10}\)
- 45\(n^{20}\)
- 5
- \(p^{4} \cdot p^{6}\)
- \(\left(p^{4}\right)^{6}\)
- \(q^{5} \cdot q^{3}\)
- \(\left(q^{5}\right)^{3}\)
- Resposta
-
- \(q^{8}\)
- \(q^{15}\)
- \(\dfrac{y^{3}}{y}\)
- \(\dfrac{y}{y^{3}}\)
- \(\dfrac{z^{6}}{z^{5}}\)
- \(\dfrac{z^{5}}{z^{6}}\)
- Resposta
-
- z
- \(\dfrac{1}{z}\)
\(\left(8 x^{5}\right)(9 x) \div 6 x^{3}\)
\((4 y)\left(12 y^{7}\right) \div 8 y^{2}\)
- Resposta
-
6\(y^{6}\)
\(\dfrac{27 a^{7}}{3 a^{3}}+\dfrac{54 a^{9}}{9 a^{5}}\)
\(\dfrac{32 c^{11}}{4 c^{5}}+\dfrac{42 c^{9}}{6 c^{3}}\)
- Resposta
-
15\(c^{6}\)
\(\dfrac{32 y^{5}}{8 y^{2}}-\dfrac{60 y^{10}}{5 y^{7}}\)
\(\dfrac{48 x^{6}}{6 x^{4}}-\dfrac{35 x^{9}}{7 x^{7}}\)
- Resposta
-
3\(x^{2}\)
\(\dfrac{63 r^{6} s^{3}}{9 r^{4} s^{2}}-\dfrac{72 r^{2} s^{2}}{6 s}\)
\(\dfrac{56 y^{4} z^{5}}{7 y^{3} z^{3}}-\dfrac{45 y^{2} z^{2}}{5 y}\)
- Resposta
-
\(-y z^{2}\)
Matemática cotidiana
Memória Um megabyte tem aproximadamente\(10^6\) bytes. Um gigabyte equivale a aproximadamente\(10^9\) bytes. Quantos megabytes existem em um gigabyte?
Memória Um gigabyte tem aproximadamente\(10^9\) bytes. Um terabyte tem aproximadamente\(10^12\) bytes. Quantos gigabytes existem em um terabyte?
- Resposta
-
\(10^{3}\)
exercícios de escrita
Jennifer acha que o quociente\(\dfrac{a^{24}}{a^{6}}\) se simplifica para\(a^{4} .\) O que há de errado com seu raciocínio?
Maurice simplifica o quociente\(\dfrac{d^{7}}{d}\) escrevendo\(\dfrac{\not{d}^7}{\not{d}}=7 .\) O que há de errado com seu raciocínio?
- Resposta
-
As respostas podem variar.
Quando Drake\((-3)^{0}\) simplificou\(-3^{0}\) e obteve a mesma resposta. Explique como usar a Ordem das Operações corretamente fornece respostas
diferentes.
Robert acha que\(x^{0}\) simplifica para 0. O que você diria para convencer Robert de que ele está errado?
- Resposta
-
As respostas podem variar.
Verificação automática
a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.
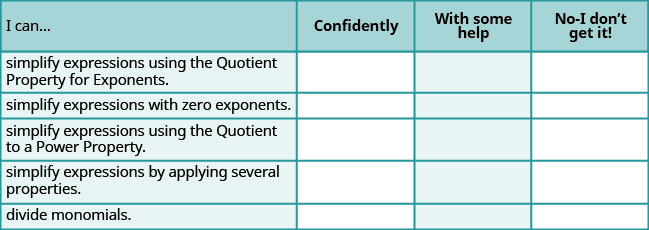
b. Em uma escala de 1 a 10, como você classificaria seu domínio desta seção à luz de suas respostas na lista de verificação? Como você pode melhorar isso?


