6.5: Divida monômios
- Page ID
- 184378
Ao final desta seção, você poderá:
- Simplifique expressões usando a propriedade de quociente para expoentes
- Simplifique expressões com zero expoentes
- Simplifique expressões usando o quociente de uma propriedade de poder
- Simplifique as expressões aplicando várias propriedades
- Divida monômios
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\dfrac{8}{24}\).
Se você perdeu esse problema, revise o Exercício 1.6.4. - Simplifique:\((2m^3)^5\).
Se você perdeu esse problema, revise o Exercício 6.2.22. - Simplifique:\(\dfrac{12x}{12y}\)
se você perdeu esse problema, revise o Exercício 1.6.10.
Simplifique expressões usando a propriedade quociente para expoentes
No início deste capítulo, desenvolvemos as propriedades dos expoentes para multiplicação. Resumimos essas propriedades abaixo.
Se a e b são números reais e m e n são números inteiros, então
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Agora, veremos as propriedades do expoente para divisão. Uma rápida atualização de memória pode ajudar antes de começarmos. Você aprendeu a simplificar frações dividindo os fatores comuns do numerador e do denominador usando a Propriedade de Frações Equivalentes. Essa propriedade também o ajudará a trabalhar com frações algébricas, que também são quocientes.
Se a, b e c são números inteiros onde\(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
Como antes, tentaremos descobrir uma propriedade examinando alguns exemplos.
\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]
Observe que, em cada caso, as bases eram as mesmas e subtraímos os expoentes.
Quando o expoente maior estava no numerador, ficamos com fatores no numerador.
Quando o expoente maior estava no denominador, ficamos com fatores no denominador — observe o numerador de 1.
Nós escrevemos:
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
Isso leva à propriedade do quociente para os expoentes.
Se a for um número real e m e n forem números inteiros, então\(a\neq 0\)
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Alguns exemplos com números podem ajudar a verificar essa propriedade.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Simplifique:
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Responda
-
Para simplificar uma expressão com um quociente, precisamos primeiro comparar os expoentes no numerador e no denominador.
1.
Desde 9 > 7, há mais fatores de x no numerador. 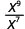
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 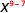
Simplifique. \(x^2\) 2.
Observe que quando o expoente maior está no numerador, ficamos com fatores no numerador.Como 10 > 2, há mais fatores de x no numerador. 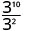
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Simplifique. \(3^8\)
Simplifique:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Responda
-
- \(x^{5}\)
- \(6^9\)
Simplifique:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Responda
-
- \(y^{6}\)
- \(10^8\)
Simplifique:
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Responda
-
Para simplificar uma expressão com um quociente, precisamos primeiro comparar os expoentes no numerador e no denominador.
1.
Desde 12 > 8, há mais fatores de b no denominador. 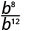
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 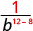
Simplifique. 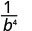
2.
Observe que quando o expoente maior está no denominador, ficamos com fatores no denominador.Como 5 > 3, há mais fatores de 3 no denominador. 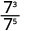
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 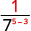
Simplifique. 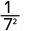
Simplifique. 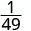
Simplifique:
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Responda
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Simplifique:
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Responda
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Observe a diferença nos dois exemplos anteriores:
- Se começarmos com mais fatores no numerador, terminaremos com fatores no numerador.
- Se começarmos com mais fatores no denominador, acabaremos com fatores no denominador.
A primeira etapa para simplificar uma expressão usando a propriedade do quociente para expoentes é determinar se o expoente é maior no numerador ou no denominador.
Simplifique:
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Responda
-
1. O expoente de um maior no numerador ou no denominador? Como 9 > 5, há mais a's no denominador e, portanto, acabaremos com fatores no denominador.
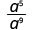
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 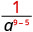
Simplifique. 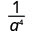
2. Observe que há mais fatores de xx no numerador, já que 11 > 7. Então, terminaremos com fatores no numerador.
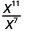
Use a propriedade do quociente,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 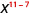
Simplifique. 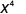
Simplifique:
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Responda
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Simplifique:
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Responda
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Simplifique expressões com um expoente de zero
Um caso especial da propriedade do quociente é quando os expoentes do numerador e do denominador são iguais, como uma expressão como\(\dfrac{a^{m}}{a^{m}}\). Do seu trabalho anterior com frações, você sabe que:
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
Em palavras, um número dividido por si só é 1. Então\(\dfrac{x}{x}=1\), para qualquer um\(x(x\neq 0)\), já que qualquer número dividido por si só é 1.
A propriedade de quociente para expoentes nos mostra como simplificar\(\dfrac{a^{m}}{a^{n}}\) quando\(m>n\) e quando\(n<m\) subtraindo expoentes. E se\(m=n\)?
Considere\(\dfrac{8}{8}\), que sabemos que é 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Agora vamos simplificar\(\dfrac{a^{m}}{a^{m}}\) de duas maneiras para nos levar à definição do expoente zero. Em geral, para\(a\neq 0\):
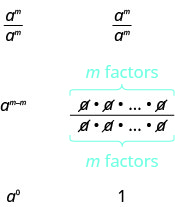
Vemos\(\dfrac{a^{m}}{a^{m}}\) simplificações para\(a^{0}\) e para 1. Então\(a^{0} = 1\).
Se a for um número diferente de zero, então\(a^{0} = 1\).
Qualquer número diferente de zero elevado à potência zero é 1.
Neste texto, assumimos que qualquer variável que elevamos à potência zero não é zero.
Simplifique:
- \(9^{0}\)
- \(n^{0}\)
- Responda
-
A definição diz que qualquer número diferente de zero elevado à potência zero é 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Simplifique:
- \(15^{0}\)
- \(m^{0}\)
- Responda
-
- 1
- 1
Simplifique:
- \(k^{0}\)
- \(29^{0}\)
- Responda
-
- 1
- 1
Agora que definimos o expoente zero, podemos expandir todas as propriedades dos expoentes para incluir expoentes de números inteiros.
Que tal elevar uma expressão à potência zero? Vamos dar uma olhada\((2x)^0\). Podemos usar o produto como uma regra de potência para reescrever essa expressão.
\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]
Isso nos diz que qualquer expressão diferente de zero elevada à potência zero é um.
Simplifique:
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Responda
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Simplifique:
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Responda
-
- 1
- 1
Simplifique:
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Responda
-
- 1
- 1
Simplifique expressões usando o quociente de uma propriedade de potência
Agora veremos um exemplo que nos levará ao quociente de uma propriedade de poder.
\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]
Observe que o expoente se aplica tanto ao numerador quanto ao denominador.
\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]
Isso leva ao quociente de uma propriedade de potência para expoentes.
Se a e b são números reais e m é um número de contagem, então\(b\neq 0\)
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
Para elevar uma fração a uma potência, eleve o numerador e o denominador para essa potência.
Um exemplo com números pode ajudar você a entender essa propriedade:
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Simplifique:
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Responda
-
1.
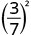
Use a propriedade do quociente,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 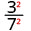
Simplifique. 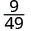
2.
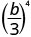
Use a propriedade do quociente,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 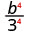
Simplifique. 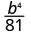
3.

Eleve o numerador e o denominador até a terceira potência. 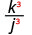
Simplifique:
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Responda
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Simplifique:
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Responda
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Simplifique as expressões aplicando várias propriedades
Agora vamos resumir todas as propriedades dos expoentes para que estejam todas juntas para nos referirmos à simplificação de expressões usando várias propriedades. Observe que agora eles estão definidos para expoentes de números inteiros.
Se a e b são números reais e m e n são números inteiros, então
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Simplifique:\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Responda
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Simplifique:\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Responda
-
\(m^{13}\)
Simplifique:\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Responda
-
\(k^{5}\)
Simplifique:\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Responda
-
\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]
Observe que depois de simplificarmos o denominador na primeira etapa, o numerador e o denominador ficaram iguais. Portanto, o valor final é igual a 1.
Simplifique\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).
- Responda
-
1
Simplifique\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).
- Responda
-
1
Simplifique:\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Responda
-
\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]
Simplifique:\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Responda
-
\(r^{8}\)
Simplifique:\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Responda
-
\(v^{6}\)
Simplifique:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Responda
-
Aqui não podemos simplificar primeiro os parênteses, pois as bases não são as mesmas.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Simplifique:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Responda
-
\(\dfrac{a^{12}}{b^{8}}\)
Simplifique:\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Responda
-
\(\dfrac{q^{21}}{r^{15}}\)
Simplifique:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Responda
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Simplifique:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Responda
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Simplifique:\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Responda
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Simplifique:\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Responda
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Simplifique:\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Responda
-
\(\dfrac{1}{a^{6}}\)
Simplifique:\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Responda
-
\(\dfrac{1}{p^{15}}\)
Simplifique:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Responda
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Simplifique:\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Responda
-
9\(r^{18}\)
Simplifique:\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Responda
-
\(\dfrac{2}{x}\)
Divida monômios
Agora você foi apresentado a todas as propriedades dos expoentes e as usou para simplificar expressões. A seguir, você verá como usar essas propriedades para dividir monômios. Posteriormente, você os usará para dividir polinômios.
Encontre o quociente:\(56 x^{7} \div 8 x^{3}\)
- Responda
-
\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]
Encontre o quociente:\(42y^{9} \div 6 y^{3}\)
- Responda
-
\(7y^{6}\)
Encontre o quociente:\(48z^{8} \div 8 z^{2}\)
- Responda
-
\(6z^{6}\)
Encontre o quociente:\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Responda
-
Quando dividimos monômios com mais de uma variável, escrevemos uma fração para cada variável.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Encontre o quociente:\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Responda
-
\(-\dfrac{9}{a^{5} b}\)
Encontre o quociente:\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Responda
-
\(\dfrac{-9 d}{c^{4}}\)
Encontre o quociente:\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Responda
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Encontre o quociente:\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Responda
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Encontre o quociente:\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Responda
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Depois de se familiarizar com o processo e praticá-lo passo a passo várias vezes, você poderá simplificar uma fração em uma etapa.
Encontre o quociente:\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Responda
-
Tenha muito cuidado para simplificar\(\dfrac{14}{21}\) dividindo um fator comum e simplificar as variáveis subtraindo seus expoentes.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Encontre o quociente:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Responda
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Encontre o quociente:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Responda
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
Em todos os exemplos até agora, não havia trabalho a ser feito no numerador ou no denominador antes de simplificar a fração. No próximo exemplo, primeiro encontraremos o produto de dois monômios no numerador antes de simplificarmos a fração. Isso segue a ordem das operações. Lembre-se de que uma barra fracionária é um símbolo de agrupamento.
Encontre o quociente:\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Responda
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Encontre o quociente:\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Responda
-
\(2 a b^{2}\)
Encontre o quociente:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Responda
-
\(-4 x y^{5}\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com a divisão de monômios:
- Expressão racional
- Dividindo monômios
- Dividindo monômios 2
Conceitos chave
- Propriedade do quociente para expoentes:
- Se a for um número real,\(a\neq 0\), e m, n são números inteiros, então:\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- Expoente zero
- Se a for um número diferente de zero, então\(a^{0} =1\).
- Quociente de uma propriedade de potência para expoentes:
- Se a e b forem números reais e mm for um número de contagem, então:\(b\neq 0\)\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- Para elevar uma fração a uma potência, eleve o numerador e o denominador para essa potência.
- Resumo das propriedades do expoente
- Se a, b são números reais e m, nm, n são números inteiros, então\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)


