6.3E: Exercícios
- Page ID
- 184397
A prática leva à perfeição
Multiplique um polinômio por um monômio
Nos exercícios a seguir, multiplique.
4\((w+10)\)
- Responda
-
4w+40
6 (b+8)
−3 (a+7)
- Responda
-
−3a−21
−5 (p+9)
2 (x−7)
- Responda
-
2x−14
7 (y−4)
−3 (k−4)
- Responda
-
−3k+12
−8 (j−5)
q (q+5)
- Responda
-
\(q^{2}+5 q\)
k (k+7)
−b (b+9)
- Responda
-
\(-b^{2}-9 b\)
−y (y+3)
−x (x−10)
- Responda
-
\(-x^{2}+10 x\)
−p (p−15)
6r (4r+s)
- Responda
-
\(24 r^{2}+6 r s\)
5c (9c+d)
12x (x−10)
- Responda
-
\(12 x^{2}-120 x\)
9 m (m−11)
−9a (3a+5)
- Responda
-
\(-27 a^{2}-45 a\)
−4p (2p+7)
3\(\left(p^{2}+10 p+25\right)\)
- Responda
-
\(3 p^{2}+30 p+75\)
6\(\left(y^{2}+8 y+16\right)\)
\(-8 x\left(x^{2}+2 x-15\right)\)
- Responda
-
\(-8 x^{3}-16 x^{2}+120 x\)
\(-5 t\left(t^{2}+3 t-18\right)\)
5\(q^{3}\left(q^{3}-2 q+6\right)\)
- Responda
-
\(5 q^{6}-10 q^{4}+30 q^{3}\)
4\(x^{3}\left(x^{4}-3 x+7\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Responda
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Responda
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Responda
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 m-9) m\)
- Responda
-
\(2 m^{2}-9 m\)
\((8 j-1) j\)
\((w-6) \cdot 8\)
- Responda
-
\(8 w-48\)
\((k-4) \cdot 5\)
4\((x+10)\)
- Responda
-
4x+40
6 (y+8)
15 (r−24)
- Responda
-
15r−360
12 (v−30)
−3 (m+11)
- Responda
-
−3m−33
−4 (p+15)
−8 (z−5)
- Responda
-
−8z+40
−3 (x−9)
u (u+5)
- Responda
-
\(u^{2}+5 u\)
\(q(q+7)\)
\(n\left(n^{2}-3 n\right)\)
- Responda
-
\(n^{3}-3 n^{2}\)
\(s\left(s^{2}-6 s\right)\)
6\(x(4 x+y)\)
- Responda
-
\(24 x^{2}+6 x y\)
5a (9a+b)
5p (11p−5q)
- Responda
-
\(55 p^{2}-25 p q\)
12\(u(3 u-4 v)\)
3\(\left(v^{2}+10 v+25\right)\)
- Responda
-
\(3 v^{2}+30 v+75\)
6\(\left(x^{2}+8 x+16\right)\)
2\(n\left(4 n^{2}-4 n+1\right)\)
- Responda
-
\(8 n^{3}-8 n^{2}+2 n\)
3\(r\left(2 r^{2}-6 r+2\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Responda
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Responda
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Responda
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 y-9) y\)
- Responda
-
\(18 y^{2}-9 y\)
\((8 b-1) b\)
Multiplique um binômio por um binômio
Nos exercícios a seguir, multiplique os seguintes binômios usando: ⓐ a Propriedade Distributiva ⓑ o método FOIL ⓒ o Método Vertical.
(w+5) (w+7)
- Responda
-
\(w^{2}+12 w+35\)
(y+9) (y+3)
(p+11) (p−4)
- Responda
-
\(p^{2}+7 p-44\)
(q+4) (q−8)
Nos exercícios a seguir, multiplique os binômios. Use qualquer método.
(x+8) (x+3)
- Responda
-
\(x^{2}+11 x+24\)
(y+7) (y+4)
(y−6) (y−2)
- Responda
-
\(y^{2}-8 y+12\)
(x−7) (x−2)
(w−4) (w+7)
- Responda
-
\(w^{2}+3 w-28\)
\((q-5)(q+8)\)
(p+12) (p−5)
- Responda
-
\(p^{2}+7 p-60\)
(m+11) (m−4)
(6p+5) (p+1)
- Responda
-
\(6 p^{2}+11 p+5\)
\((7 m+1)(m+3)\)
(2t−9) (10t+1)
- Responda
-
\(20 t^{2}-88 t-9\)
(3r−8) (11r+1)
(5x−y) (3x−6)
- Responda
-
\(15 x^{2}-3 x y-30 x+6 y\)
(10a−b) (3a−4)
(a+b) (2a+3b)
- Responda
-
\(2 a^{2}+5 a b+3 b^{2}\)
(r+s) (3r+2s)
(4z−y) (z−6)
- Responda
-
\(4 z^{2}-24 z-z y+6 y\)
(5x−y) (x−4)
\(\left(x^{2}+3\right)(x+2)\)
- Responda
-
\(x^{3}+2 x^{2}+3 x+6\)
\(\left(y^{2}-4\right)(y+3)\)
\(\left(x^{2}+8\right)\left(x^{2}-5\right)\)
- Responda
-
\(x^{4}+3 x^{2}-40\)
\(\left(y^{2}-7\right)\left(y^{2}-4\right)\)
(5ab−1) (2ab+3)
- Responda
-
\(10 a^{2} b^{2}+13 a b-3\)
(2xy+3) (3xy+2)
(6pq−3) (4pq−5)
- Responda
-
\(24 p^{2} q^{2}-42 p q+15\)
(3rs−7) (3rs−4)
Multiplique um trinômio por um binômio
Nos exercícios a seguir, multiplique usando ⓐ a Propriedade Distributiva ⓑ e o Método Vertical.
\((x+5)\left(x^{2}+4 x+3\right)\)
- Responda
-
\(x^{3}+9 x^{2}+23 x+15\)
\((u+4)\left(u^{2}+3 u+2\right)\)
\((y+8)\left(4 y^{2}+y-7\right)\)
- Responda
-
\(4 y^{3}+33 y^{2}+y-56\)
\((a+10)\left(3 a^{2}+a-5\right)\)
Nos exercícios a seguir, multiplique. Use qualquer um dos métodos.
\((w-7)\left(w^{2}-9 w+10\right)\)
- Responda
-
\(w^{3}-16 w^{2}+73 w-70\)
\((p-4)\left(p^{2}-6 p+9\right)\)
\((3 q+1)\left(q^{2}-4 q-5\right)\)
- Responda
-
\(3 q^{3}-11 q^{2}-19 q-5\)
\((6 r+1)\left(r^{2}-7 r-9\right)\)
Prática m
(10y−6) + (4y−7)
- Responda
-
14e−13
(15p−4) + (3p−5)
\(\left(x^{2}-4 x-34\right)-\left(x^{2}+7 x-6\right)\)
- Responda
-
−11x−28
\(\left(j^{2}-8 j-27\right)-\left(j^{2}+2 j-12\right)\)
5\(q\left(3 q^{2}-6 q+11\right)\)
- Responda
-
\(15 q^{3}-30 q^{2}+55 q\)
8\(t\left(2 t^{2}-5 t+6\right)\)
(s−7) (s+9)
- Responda
-
\(s^{2}+2 s-63\)
(x−5) (x+13)
\(\left(y^{2}-2 y\right)(y+1)\)
- Resposta
-
\(y^{3}-y^{2}-2 y\)
\(\left(a^{2}-3 a\right)(4 a+5)\)
\((3 n-4)\left(n^{2}+n-7\right)\)
- Resposta
-
\(3 n^{3}-n^{2}-25 n+28\)
\((6 k-1)\left(k^{2}+2 k-4\right)\)
\((7 p+10)(7 p-10)\)
- Resposta
-
\(49 p^{2}-100\)
(3y+8) (3y−8)
\(\left(4 m^{2}-3 m-7\right) m^{2}\)
- Resposta
-
\(4 m^{4}-3 m^{3}-7 m^{2}\)
\(\left(15 c^{2}-4 c+5\right) c^{4}\)
\((5 a+7 b)(5 a+7 b)\)
- Resposta
-
\(25 a^{2}+70 a b+49 b^{2}\)
(3x−11y) (3x−11y)
(4y+12z) (4y−12z)
- Resposta
-
\(16 y^{2}-144 z^{2}\)
Matemática cotidiana
Matemática mental Você pode usar a multiplicação binomial para multiplicar números sem uma calculadora. Digamos que você precise multiplicar 13 vezes 15. Pense em 13 como 10+3 e 15 como 10+5.
- Multiplique (10+3) (10+5) pelo método FOIL.
- Multiplique 13,15 sem usar uma calculadora.
- Qual caminho é mais fácil para você? Por quê?
Matemática mental Você pode usar a multiplicação binomial para multiplicar números sem uma calculadora. Digamos que você precise multiplicar 18 vezes 17. Pense em 18 como 20−2 e 17 como 20−3.
- Multiplique (20−2) (20−3) pelo método FOIL.
- Multiplique 18,17 sem usar uma calculadora.
- Qual caminho é mais fácil para você? Por quê?
- Resposta
-
- 306
- 306
- As respostas podem variar.
exercícios de escrita
Qual método você prefere usar ao multiplicar dois binômios: a propriedade distributiva, o método FOIL ou o método vertical? Por quê?
Qual método você prefere usar ao multiplicar um trinômio por um binômio: a propriedade distributiva ou o método vertical? Por quê?
- Resposta
-
As respostas podem variar.
Multiplique o seguinte:
\(\begin{array}{l}{(x+2)(x-2)} \\ {(y+7)(y-7)} \\ {(w+5)(w-5)}\end{array}\)
Explique o padrão que você vê em suas respostas.
Multiplique o seguinte:
\(\begin{array}{l}{(m-3)(m+3)} \\ {(n-10)(n+10)} \\ {(p-8)(p+8)}\end{array}\)
Explique o padrão que você vê em suas respostas.
- Resposta
-
As respostas podem variar.
Multiplique o seguinte:
\(\begin{array}{l}{(p+3)(p+3)} \\ {(q+6)(q+6)} \\ {(r+1)(r+1)}\end{array}\)
Explique o padrão que você vê em suas respostas.
Multiplique o seguinte:
\(\begin{array}{l}{(x-4)(x-4)} \\ {(y-1)(y-1)} \\ {(z-7)(z-7)}\end{array}\)
Explique o padrão que você vê em suas respostas.
- Resposta
-
As respostas podem variar.
Verificação automática
a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.
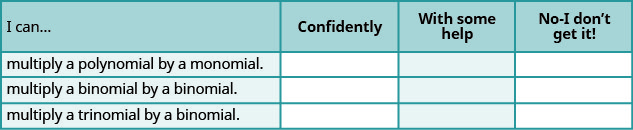
b. O que essa lista de verificação lhe diz sobre o seu domínio desta seção? Quais etapas você tomará para melhorar?


