6.4: Produtos especiais
- Page ID
- 184406
Ao final desta seção, você poderá:
- Elabore um binômio usando o Padrão de Quadrados Binomiais
- Multiplique conjugados usando o padrão Produto de Conjugados
- Reconheça e use o padrão de produto especial apropriado
Antes de começar, faça este teste de prontidão.
Simplifique: a.\(9^2\) b.\((−9)^2\)\(−9^2\) c.
Se você perdeu esse problema, revise o Exercício 1.5.13.
Quadrar um binômio usando o padrão de quadrados binomiais
Os matemáticos gostam de procurar padrões que facilitem seu trabalho. Um bom exemplo disso é o quadrado de binômios. Embora você sempre possa obter o produto escrevendo o binômio duas vezes e usando os métodos da última seção, há menos trabalho a ser feito se você aprender a usar um padrão.
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
Veja esses resultados. Você vê algum padrão?
E quanto ao número de termos? Em cada exemplo, colocamos um binômio ao quadrado e o resultado foi um trinômio.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
Agora, veja o primeiro termo em cada resultado. De onde veio isso?
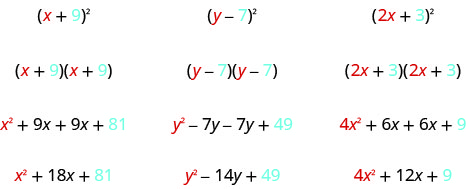
O primeiro termo é o produto dos primeiros termos de cada binômio. Como os binômios são idênticos, é apenas o quadrado do primeiro termo!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
Para obter o primeiro termo do produto, eleve ao quadrado o primeiro termo.
De onde veio o último termo? Veja os exemplos e encontre o padrão.
O último termo é o produto dos últimos termos, que é o quadrado do último termo.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
Para obter o último termo do produto, eleve ao quadrado o último termo.
Finalmente, veja o médio prazo. Observe que isso veio da adição dos termos “externo” e “interno”, que são ambos iguais! Portanto, o termo médio é o dobro do produto dos dois termos do binômio.
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
Para obter o prazo médio do produto, multiplique os termos e duplique o produto.
Juntando tudo:
Se\(a\) e\(b\) forem números reais, o padrão binomial quadrado é
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
Aplicando isso a dois tipos binomiais:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
Para quadrar um binômio:
- quadrado o primeiro termo
- quadrado o último termo
- dobrar seu produto
Um exemplo numérico ajuda a verificar o padrão.
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
Para multiplicar,\((10+4)^2\) normalmente você seguiria a Ordem das Operações.
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
O padrão funciona!
\(\text { Multiply: }(x+5)^{2}\)
Solução:
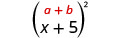 |
|
| Efetue o quadrado do primeiro termo. |  |
| Elabore o último termo. |  |
| Duplique o produto. |  |
| Simplifique. | \(x^{2}+10 x+25\) |
Multiplique:\((x+9)^{2}\)
- Resposta
-
\(x^{2}+18 x+81\)
Multiplique:\((y+11)^{2}\)
- Resposta
-
\(y^{2}+22 y+121\)
Multiplique:\((y-3)^{2}\)
Solução:
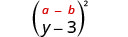 |
|
| Efetue o quadrado do primeiro termo. |  |
| Elabore o último termo. |  |
| Duplique o produto. | 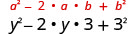 |
| Simplifique. | \(y^{2}-6 y+9\) |
Multiplique:\((x-9)^{2}\)
- Resposta
-
\(x^{2}-18 x+81\)
Multiplique:\((p-13)^{2}\)
- Resposta
-
\(p^{2}-26 p+169\)
Multiplique:\((4 x+6)^{2}\)
Solução:
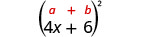 |
|
| Use o padrão. | 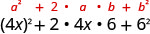 |
| Simplifique. | \(16 x^{2}+48 x+36\) |
Multiplique:\((6 x+3)^{2}\)
- Resposta
-
\(36 x^{2}+36 x+9\)
Multiplique:\((4 x+9)^{2}\)
- Resposta
-
\(16 x^{2}+72 x+81\)
Multiplique:\((2 x-3 y)^{2}\)
Solução:
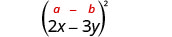 |
|
| Use o padrão. | 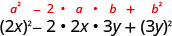 |
| Simplifique. | \(4 x^{2}-12 x y+9 y^{2}\) |
Multiplique:\((2 c-d)^{2}\)
- Resposta
-
\(4 c^{2}-4 c d+d^{2}\)
Multiplique:\((4 x-5 y)^{2}\)
- Resposta
-
\(16 x^{2}-40 x y+25 y^{2}\)
Multiplique:\(\left(4 u^{3}+1\right)^{2}\)
Solução:
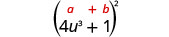 |
|
| Use o padrão. | 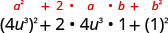 |
| Simplifique. | \(16 u^{6}+8 u^{3}+1\) |
Multiplique:\(\left(2 x^{2}+1\right)^{2}\)
- Resposta
-
\(4 x^{4}+4 x^{2}+1\)
Multiplique:\(\left(3 y^{3}+2\right)^{2}\)
- Resposta
-
\(9 y^{6}+12 y^{3}+4\)
Multiplique conjugados usando o produto do padrão de conjugados
Acabamos de ver um padrão para quadrar binômios que podemos usar para facilitar a multiplicação de alguns binômios. Da mesma forma, há um padrão para outro produto de binômios. Mas antes de chegarmos a isso, precisamos introduzir um pouco de vocabulário.
O que você percebe sobre esses pares de binômios?
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
Veja o primeiro termo de cada binômio em cada par.
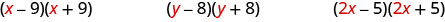
Observe que os primeiros termos são os mesmos em cada par.
Veja os últimos termos de cada binômio em cada par.
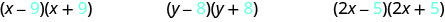
Observe que os últimos termos são os mesmos em cada par.
Observe como cada par tem uma soma e uma diferença.
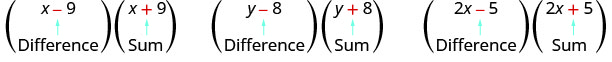
Um par de binômios em que cada um tem o mesmo primeiro termo e o mesmo último termo, mas um é uma soma e outro é uma diferença tem um nome especial. É chamado de par conjugado e tem a forma (a−b), (a+b).
Um par conjugado são dois binômios da forma
\[(a-b),(a+b)\nonumber \]
Cada par de binômios tem o mesmo primeiro termo e o mesmo último termo, mas um binômio é uma soma e o outro é uma diferença.
Existe um bom padrão para encontrar o produto dos conjugados. Você poderia, é claro, simplesmente FOIL para obter o produto, mas usar o padrão facilita seu trabalho.
Vamos procurar o padrão usando FOIL para multiplicar alguns pares conjugados.
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
Cada primeiro termo é o produto dos primeiros termos dos binômios e, como são idênticos, é o quadrado do primeiro termo.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
O último termo veio da multiplicação dos últimos termos, o quadrado do último termo.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
O que você observa sobre os produtos?
O produto dos dois binômios também é um binômio! A maioria dos produtos resultantes do FOIL são trinômios.
Por que não existe um termo intermediário? Observe que os dois termos intermediários que você obtém de FOIL se combinam com 0 em todos os casos, o resultado de uma adição e uma subtração.
O produto dos conjugados é sempre da forma\(a^2-b^2\). Isso é chamado de diferença de quadrados.
Isso leva ao padrão:
Se\(a\) e\(b\) forem números reais,

O produto é chamado de diferença de quadrados.
Para multiplicar os conjugados, eleve ao quadrado o primeiro termo, eleve ao quadrado o último termo e escreva o produto como uma diferença de quadrados.
Vamos testar esse padrão com um exemplo numérico.
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
Observe que o resultado é o mesmo!
Multiplique:\((x-8)(x+8)\)
Solução:
Primeiro, reconheça isso como um produto de conjugados. Os binômios têm os mesmos primeiros termos e os mesmos últimos termos, e um binômio é uma soma e o outro é uma diferença.
| Ele se encaixa no padrão. | 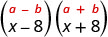 |
| Eleve ao quadrado o primeiro termo, x. | 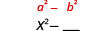 |
| Eleve ao quadrado o último termo, 8. | 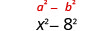 |
| O produto é uma diferença de quadrados. | 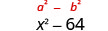 |
Multiplique:\((x-5)(x+5)\)
- Resposta
-
\(x^{2}-25\)
Multiplique:\((w-3)(w+3)\)
- Resposta
-
\(w^{2}-9\)
Multiplique:\((2 x+5)(2 x-5)\)
Solução:
Os binômios são conjugados?
| É o produto dos conjugados. | 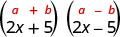 |
| Eleve ao quadrado o primeiro termo, 2 x. | 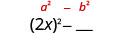 |
| Eleve ao quadrado o último termo, 5. | 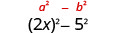 |
| Simplifique. O produto é uma diferença de quadrados. | 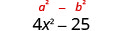 |
Multiplique:\((6 x+5)(6 x-5)\)
- Resposta
-
\(36 x^{2}-25\)
Multiplique:\((2 x+7)(2 x-7)\)
- Resposta
-
\(4 x^{2}-49\)
Os binômios no próximo exemplo podem olhar para trás — a variável está no segundo termo. Mas os dois binômios ainda são conjugados, então usamos o mesmo padrão para multiplicá-los.
Encontre o produto:\((3+5 x)(3-5 x)\)
Solução:
| É o produto dos conjugados. | 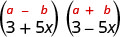 |
| Use o padrão. | 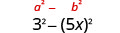 |
| Simplifique. | \(9-25 x^{2}\) |
Multiplique:\((7+4 x)(7-4 x)\)
- Resposta
-
\(49-16 x^{2}\)
Multiplique:\((9-2 y)(9+2 y)\)
- Resposta
-
\(81-4 y^{2}\)
Agora vamos multiplicar os conjugados que têm duas variáveis.
Encontre o produto:\((5 m-9 n)(5 m+9 n)\)
Solução:
| Isso se encaixa no padrão. | 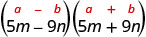 |
| Use o padrão. | 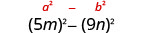 |
| Simplifique. | \(25 m^{2}-81 n^{2}\) |
Encontre o produto:\((4 p-7 q)(4 p+7 q)\)
- Resposta
-
\(16 p^{2}-49 q^{2}\)
Encontre o produto:\((3 x-y)(3 x+y)\)
- Resposta
-
\(9 x^{2}-y^{2}\)
Encontre o produto:\((c d-8)(c d+8)\)
Solução:
| Isso se encaixa no padrão. | 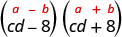 |
| Use o padrão. | 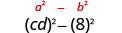 |
| Simplifique. | \(c^{2} d^{2}-64\) |
Encontre o produto:\((x y-6)(x y+6)\)
- Resposta
-
\(x^{2} y^{2}-36\)
Encontre o produto:\((a b-9)(a b+9)\)
- Resposta
-
\(a^{2} b^{2}-81\)
Encontre o produto:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
Solução:
| Isso se encaixa no padrão. | 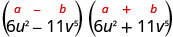 |
| Use o padrão. | 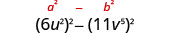 |
| Simplifique. | \(36 u^{4}-121 v^{10}\) |
Encontre o produto:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- Resposta
-
\(9 x^{4}-16 y^{6}\)
Encontre o produto:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- Resposta
-
\(4 m^{4}-25 n^{6}\)
Reconheça e use o padrão de produto especial apropriado
Acabamos de desenvolver padrões de produtos especiais para quadrados binomiais e para o produto de conjugados. Os produtos têm uma aparência semelhante, por isso é importante reconhecer quando é apropriado usar cada um desses padrões e observar como eles diferem. Veja os dois padrões juntos e observe suas semelhanças e diferenças.
\(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)
Escolha o padrão apropriado e use-o para encontrar o produto:
- \((2 x-3)(2 x+3)\)
- \((8 x-5)^{2}\)
- \((6 m+7)^{2}\)
- \((5 x-6)(6 x+5)\)
Solução:
1. \((2x−3)(2x+3)\)Esses são conjugados. Eles têm os mesmos primeiros números e os mesmos últimos números, e um binômio é uma soma e o outro é uma diferença. Ele se encaixa no padrão Produto de Conjugados.
| Isso se encaixa no padrão. | 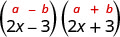 |
| Use o padrão. | 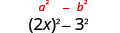 |
| Simplifique. | \(4 x^{2}-9\) |
2. \((8 x-5)^{2}\)Somos convidados a quadrar um binômio. Ele se encaixa no padrão de quadrados binomiais.
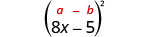 |
|
| Use o padrão. |  |
| Simplifique. | \(64 x^{2}-80 x+25\) |
3. \((6 m+7)^{2}\)Novamente, vamos quadrar um binômio, então usaremos o padrão de quadrados binomiais.
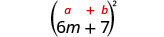 |
|
| Use o padrão. |  |
| Simplifique. | \(36 m^{2}+84 m+49\) |
4. \((5 x-6)(6 x+5)\)Este produto não se encaixa nos padrões, então usaremos FOIL.
\(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)
Escolha o padrão apropriado e use-o para encontrar o produto:
- \((9b−2)(2b+9)\)
- \((9p−4)2\)
- \((7y+1)^2\)
- \((4r-3)(4r+3)\)
- Resposta
-
- PAPEL ALUMÍNIO;\(18 b^{2}+77 b-18\)
- Quadrados binomiais;\(81 p^{2}-72 p+16\)
- Quadrados binomiais;\(49 y^{2}+14 y+1\)
- Produto de conjugados;\(16 r^{2}-9\)
Escolha o padrão apropriado e use-o para encontrar o produto:
- \((6x+7)^2\)
- \((3x−4)(3x+4)\)
- \((2x−5)(5x−2)\)
- \((6n−1)^2\)
- Resposta
-
- Quadrados binomiais;\(36 x^{2}+84 x+49\)
- Produto de conjugados;\(9 x^{2}-16\)
- PAPEL ALUMÍNIO;\(10 x^{2}-29 x+10\)
- Quadrados binomiais;\(36 n^{2}-12 n+1\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com produtos especiais:
- Produtos especiais
Conceitos-chave
- Padrão de quadrados binomiais
- Se a, b são números reais,
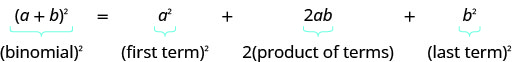
- \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
- \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
- Para quadrar um binômio: eleve ao quadrado o primeiro termo, ao quadrado do último termo, dobre seu produto.
- Se a, b são números reais,
- Produto do padrão de conjugados
- Se a, ba, b são números reais,
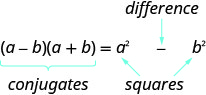
- \((a-b)(a+b)=a^{2}-b^{2}\)
- O produto é chamado de diferença de quadrados.
- Se a, ba, b são números reais,
- Para multiplicar os conjugados:
- quadrado o primeiro termo quadrado o último termo escreva-o como uma diferença de quadrados
Glossário
- par conjugado
- Um par conjugado são dois binômios da forma\((a−b)\) e\((a+b)\); cada par de binômios tem o mesmo primeiro termo e o mesmo último termo, mas um binômio é uma soma e o outro é uma diferença.


