6.3: Multiplicar polinômios

Last updated
Save as PDF

Page ID: 184390

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Multiplique um polinômio por um monômio
Multiplique um binômio por um binômio
Multiplique um trinômio por um binômio

Nota

Antes de começar, faça este teste de prontidão.

Distribua:$2(x+3)$.
Se você perdeu esse problema, revise o Exercício 1.10.31.
Combine termos semelhantes:$x^{2}+9x+7x+63$.
Se você perdeu esse problema, revise o Exercício 1.3.37.

Multiplique um polinômio por um monômio

Usamos a propriedade distributiva para simplificar expressões como$2(x−3)$. Você multiplicou os dois termos entre parênteses$x$ e$3$, por$2$, para obter$2x−6$. Com o novo vocabulário deste capítulo, você pode dizer que estava multiplicando um binômio,$x−3$, por um monômio,$2$.

Multiplicar um binômio por um monômio não é novidade para você! Aqui está um exemplo:

Exercício$\PageIndex{1}$

Multiplique:$4(x+3)$.

Resposta

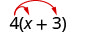
	$4 vezes x mais 3. Duas setas se estendem de 4, terminando em x e 3.$
Distribuir.	$4 \cdot x+4 \cdot 3$
Simplifique.	$4 x+12$

Exercício$\PageIndex{2}$

Multiplique:$5(x+7)$.

Resposta: 5x+35

Exercício$\PageIndex{3}$

Multiplique:$3(y+13)$.

Resposta: 3a+39

Exercício$\PageIndex{4}$

Multiplique: y (y−2).

Resposta

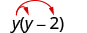
	$y vezes y menos 2. Duas setas se estendem do coeficiente y, terminando em y e menos 2 entre parênteses.$
Distribuir.	$y \cdot y-y \cdot 2$
Simplifique.	$y^{2}-2 y$

Exercício$\PageIndex{5}$

Multiplique:$x(x−7)$.

Resposta: $x^{2}-7 x$

Exercício$\PageIndex{6}$

Multiplique:$d(d−11)$.

Resposta: $d^{2}-11d$

Exercício$\PageIndex{7}$

Multiplique:$7x(2 x+y)$

Resposta

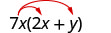
	$7 x vezes 2 x mais y. Duas setas se estendem de 7x, terminando em 2x e y.$
Distribuir.	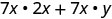$7 x vezes 2 x mais 7 x vezes y.$
Simplifique.	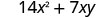$14 x ao quadrado mais 7 x y.$

Exercício$\PageIndex{8}$

Multiplique:$5x(x+4 y)$

Resposta: $5 x^{2}+20 x y$

Exercício$\PageIndex{9}$

Multiplique:$2p(6 p+r)$

Resposta: $12 p^{2}+2 p r$

Exercício$\PageIndex{10}$

Multiplique:$-2 y\left(4 y^{2}+3 y-5\right)$

Resposta

	$Menos 2 y vezes 4 y ao quadrado mais 3 y menos 5. Três setas se estendem de menos 2 y, terminando em 4 y ao quadrado, 3 y e menos 5.$
Distribuir.	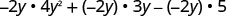$Menos 2 y vezes 4 y ao quadrado mais menos 2 y vezes 3 y menos menos menos 2 y vezes 5.$
Simplifique.	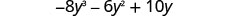$Menos 8 y ao cubo menos 6 y ao quadrado mais 10 y.$

Exercício$\PageIndex{11}$

Multiplique:$-3 y\left(5 y^{2}+8 y-7\right)$

Resposta: $-15 y^{3}-24 y^{2}+21 y$

Exercício$\PageIndex{12}$

Multiplique:$4x^{2}\left(2 x^{2}-3 x+5\right)$

Resposta: $8 x^{4}-24 x^{3}+20 x^{2}$

Exercício$\PageIndex{13}$

Multiplique:$2x^{3}\left(x^{2}-8 x+1\right)$

Resposta

	$2 x vezes ao cubo x ao quadrado menos 8 x mais 1. Três setas se estendem de 2 x ao cubo, terminando em x ao quadrado, menos 8 x e 1.$
Distribuir.	$2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1$
Simplifique.	$2 x^{5}-16 x^{4}+2 x^{3}$

Exercício$\PageIndex{14}$

Multiplique: 4$x\left(3 x^{2}-5 x+3\right)$

Resposta: $12 x^{3}-20 x^{2}+12 x$

Exercício$\PageIndex{15}$

Multiplique:$-6 a^{3}\left(3 a^{2}-2 a+6\right)$

Resposta: $-18 a^{5}+12 a^{4}-36 a^{3}$

Exercício$\PageIndex{16}$

Multiplique:$(x+3) p$

Resposta

O monômio é o segundo fator.	$x mais 3, entre parênteses, vezes p. Duas setas se estendem do p, terminando em x e 3.$
Distribuir.	$x \cdot p+3 \cdot p$
Simplifique.	\ (\ x p+3 p)

Exercício$\PageIndex{17}$

Multiplique:$(x+8) p$

Resposta: $x p+8 p$

Exercício$\PageIndex{18}$

Multiplique:$(a+4) p$

Resposta: $a p+4 p$

Multiplique um binômio por um binômio

Assim como existem diferentes maneiras de representar a multiplicação de números, existem vários métodos que podem ser usados para multiplicar um binômio vezes um binômio. Começaremos usando a propriedade distributiva.

Multiplique um binômio por um binômio usando a propriedade distributiva

Veja o Exercício$\PageIndex{16}$, onde multiplicamos um binômio por um monômio.

Instruções	Expressão
Expressões iniciais	$x mais 3, entre parênteses, vezes p. Duas setas se estendem do p, terminando em x e 3.$
Distribuímos o$p$ para obter:	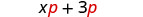$x p mais 3 p.$
E se tivermos$(x + 7)$ em vez de$p$?	$x mais 3 multiplicado por x mais 7. Duas setas se estendem de x mais 7, terminando em x e 3 no primeiro binômio.$
Distribuir$(x + 7)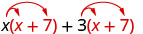$.	$A soma de dois produtos. O produto de x e x mais 7, mais o produto de 3 e x mais 7.$
Distribua novamente.	$x^{2}+7 x+3 x+21$
Combine termos semelhantes.	$x^{2}+10 x+21$

Observe que antes de combinar termos semelhantes, você tinha quatro termos. Você multiplicou os dois termos do primeiro binômio pelos dois termos do segundo binômio — quatro multiplicações.

Exercício$\PageIndex{19}$

Multiplique:$(y+5)(y+8)$

Resposta

	$O produto de dois binômios, y mais 5 e y mais 8. Duas setas se estendem de y mais 8, terminando em y e 5 no primeiro binômio.$
Distribua (y + 8).	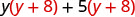$A soma de dois produtos, o produto de y e y mais 8, mais o produto de 5 e y mais 8.$
Distribua novamente	$y^{2}+8 y+5 y+40$
Combine termos semelhantes.	\ (\ y^ {2} +13 a+40)

Exercício$\PageIndex{20}$

Multiplique:$(x+8)(x+9)$

Resposta: $x^{2}+17 x+72$

Exercício$\PageIndex{21}$

Multiplique:$(5 x+9)(4 x+3)$

Resposta: $20 x^{2}+51 x+27$

Exercício$\PageIndex{22}$

Multiplique:$(2 y+5)(3 y+4)$

Resposta

	$O produto de dois binômios, 2 y mais 5 e 3 y mais 4. Duas setas se estendem de 3y mais 4, terminando em 2y e 5 no primeiro binômio.$
Distribua (3 y + 4).	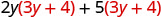$A soma de dois produtos, o produto de 2 y e 3 y mais 4, mais o produto de 5 e 3 y mais 4.$
Distribua novamente	$6 y^{2}+8 y+15 y+20$
Combine termos semelhantes.	$6 y^{2}+23 y+20$

Exercício$\PageIndex{23}$

Multiplique:$(3 b+5)(4 b+6)$

Resposta: $12 b^{2}+38 b+30$

Exercício$\PageIndex{24}$

Multiplique:$(a+10)(a+7)$

Resposta: $a^{2}+17 a+70$

Exercício$\PageIndex{25}$

Multiplique:$(4 y+3)(2 y-5)$

Resposta

	$Exemplo: 6.36.jpg$
Distribuir.	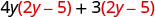$A soma de dois produtos, o produto de 4y e 2y menos 5, mais o produto de 3 e 2y menos 5.$
Distribua novamente.	$8 y^{2}-20 y+6 y-15$
Combine termos semelhantes.	$8 y^{2}-14 y-15$

Exercício$\PageIndex{26}$

Multiplique:$(5 y+2)(6 y-3)$

Resposta: $30 y^{2}-3 y-6$

Exercício$\PageIndex{27}$

Multiplique:$(3 c+4)(5 c-2)$

Resposta: $15 c^{2}+14 c-8$

Exercício$\PageIndex{28}$

Multiplique:$(x-2)(x-y)$

Resposta

	$O produto de dois binômios, x menos 2 e x menos y. Duas setas se estendem de x menos y, terminando em x e 2 no primeiro binômio.$
Distribuir.	$A diferença de dois produtos. O produto de x e x menos 7, menos o produto de 2 e x menos y.$
Distribua novamente.	$x^{2}-x y-2 x+2 y$
Não há termos semelhantes para combinar.

Exercício$\PageIndex{29}$

Multiplique:$(a+7)(a-b)$

Resposta: $a^{2}-a b+7 a-7 b$

Exercício$\PageIndex{30}$

Multiplique:$(x+5)(x-y)$

Resposta: $x^{2}-x y+5 x-5 y$

Multiplique um binômio por um binômio usando o método FOIL

Lembre-se de que quando você multiplica um binômio por um binômio, você obtém quatro termos. Às vezes, você pode combinar termos semelhantes para obter um trinômio, mas às vezes, como no Exercício$\PageIndex{28}$, não há termos semelhantes para combinar.

Vamos dar uma olhada no último exemplo novamente e prestar atenção especial à forma como obtivemos os quatro termos.

\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber\]

De onde veio o primeiro termo$x^{2}$,,?

$Esta figura explica como multiplicar um binômio usando o método FOIL. Tem duas colunas, com instruções escritas à esquerda e matemática à direita. Na parte superior da figura, o texto na coluna da esquerda diz “É o produto de x e x, os primeiros termos em x menos 2 e x menos y”. Na coluna da direita está o produto de x menos 2 e x menos y. Uma seta se estende do x em x menos 2 e termina no x em x menos y. Abaixo está a palavra “Primeiro”. Uma linha abaixo, o texto na coluna da esquerda diz “Os próximos termos, menos xy, são o produto de x e menos y, os dois termos externos”. Na coluna da direita está o produto de x menos 2 e x menos y, com outra seta se estendendo do x em x menos 2 até o y em x menos y. Abaixo está a palavra “Externo”. Uma linha abaixo, o texto na coluna da esquerda diz “O terceiro termo, menos 2 x, é o produto de menos 2 e x, os dois termos internos”. Na coluna da direita está o produto de x menos 2 e x menos y com uma terceira seta que se estende de menos 2 em x menos 2 e terminando em x menos y. Abaixo está a palavra “Interno”. Na última linha, o texto na coluna da esquerda diz “E o último termo, mais 2y, veio da multiplicação dos dois últimos termos, menos 2 e menos y”. Na coluna da direita está o produto de x menos 2 e x menos y, com uma quarta seta se estendendo de menos 2 em x menos 2 até menos y em x menos y. Abaixo está a palavra “Último”.$

Nós abreviamos “First, Outer, Inner, Last” como FOIL. As letras representam “F primeiro, O externo, I interno, L último”. A palavra FOIL é fácil de lembrar e garante que encontremos todos os quatro produtos.

\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}\]

Vamos dar uma olhada em (x+3) (x+7).

Propriedade distributiva	FOLHA
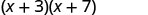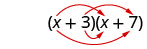$O produto de x mais 3 e x mais 7.$	$O produto de x mais 3 e x mais y. Uma seta se estende do x em x mais 3 até o x em x mais 7. Uma segunda seta se estende do x em x mais 3 até o 7 em x mais 7. Uma terceira seta se estende do 3 em x mais 3 até o x em x mais 7. Uma quarta seta se estende do 3 em x mais 3 até o 7 em x mais 7.$
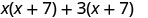$A soma de dois produtos, o produto de x e x mais 7 e o produto de 3 e x mais 7.$
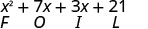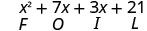$x ao quadrado mais 7 x mais 3 x mais 21. Abaixo de x ao quadrado está a letra F, abaixo de 7 x está a letra O, abaixo de 3 x está a letra I e abaixo de 21 está a letra L, soletrando FOIL.$	$x ao quadrado mais 7 x mais 3 x mais 21. Abaixo de x ao quadrado está a letra F, abaixo de 7 x está a letra O, abaixo de 3 x está a letra I e abaixo de 21 está a letra L, soletrando FOIL.$
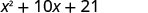$x ao quadrado mais 10 x mais 21.$	$x^{2}+10 x+21$

Observe como os termos na terceira linha se encaixam no padrão FOIL.

Agora vamos fazer um exemplo em que usamos o padrão FOIL para multiplicar dois binômios.

Exercício$\PageIndex{31}$: How to Multiply a Binomial by a Binomial using the FOIL Method

Multiplique usando o método FOIL:$(x+5)(x+9)$

Resposta: $Essa figura é uma tabela que tem três colunas e cinco linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda e a terceira colunas contêm matemática. Na linha superior da tabela, a primeira célula à esquerda diz “Etapa 1. Multiplique os primeiros termos.” A segunda coluna contém o produto dos binômios x mais 5 e x mais 9. Abaixo disso está o produto de x mais 5 e x mais 9 novamente, com uma seta que se estende do x no primeiro binômio até o x no segundo binômio. A terceira coluna contém x ao quadrado mais branco mais branco mais branco mais em branco. Abaixo do quadrado x está a letra F, e abaixo de cada um dos três espaços em branco estão as letras O, I e L, respectivamente.$
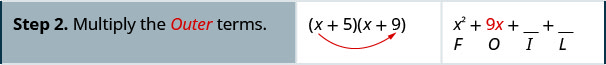
$Na segunda linha, a primeira célula diz “Etapa 2. Multiplique os termos externos.” Na segunda célula está o produto de x mais 5 e x mais 9 novamente, com uma seta que se estende de x no primeiro binômio até o 9 no segundo binômio. A terceira célula contém x ao quadrado mais 9x mais branco mais branco, com a letra F abaixo do x ao quadrado, O abaixo de 9x e I e L abaixo dos dois espaços em branco.$
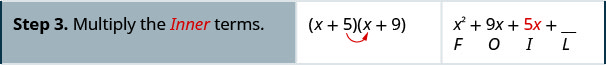
$Na terceira linha, a primeira célula diz “Etapa 3. Multiplique os termos internos.” A segunda célula contém o produto de x mais 5 e x mais 9 novamente, com uma seta que se estende de 5 no primeiro binômio até o x no segundo binômio. A terceira célula contém x ao quadrado mais 9x mais 5x mais branco, com F abaixo de x ao quadrado, O abaixo de 9x, I abaixo de 5x e L abaixo do espaço em branco.$
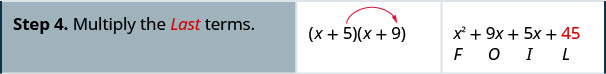
$Na quarta linha, a primeira célula diz “Etapa 4. Multiplique os últimos termos.” Na segunda célula está o produto de x mais 5 e x mais 9 novamente, com uma seta que se estende de 5 no primeiro binômio até 9 no segundo binômio. A terceira célula contém x ao quadrado mais 9x mais 6x mais 45, com F abaixo de x ao quadrado, O abaixo de 9x, I abaixo de 6x e L abaixo de 45.$
$Na última linha, a primeira célula diz “Etapa 5. Combine termos semelhantes, sempre que possível.” A segunda célula está em branco. A terceira célula contém a expressão final: x ao quadrado mais 15x mais 45.$

Exercício$\PageIndex{32}$

Multiplique usando o método FOIL:$(x+6)(x+8)$

Resposta: $x^{2}+14 x+48$

Exercício$\PageIndex{33}$

Multiplique usando o método FOIL:$(y+17)(y+3)$

Resposta: $y^{2}+20 y+51$

Resumimos as etapas do método FOIL abaixo. O método FOIL só se aplica à multiplicação de binômios, não a outros polinômios!

MULTIPLIQUE DOIS BINÔMIOS USANDO O MÉTODO FOIL

$.$

Quando você multiplica pelo método FOIL, desenhar as linhas ajudará seu cérebro a se concentrar no padrão e facilitará sua aplicação.

Exercício$\PageIndex{34}$

Multiplique:$(y−7)(y+4)$.

Resposta: $Essa figura tem três colunas, com instruções escritas na primeira coluna e matemática na segunda e terceira colunas. Na parte superior da figura, o texto na primeira coluna diz “Multiplique os primeiros termos”. A segunda coluna contém o produto de dois binômios, y menos 7 e y mais 4, com uma seta que se estende do y no primeiro binômio até o y no segundo binômio. A terceira coluna contém y ao quadrado mais branco mais em branco mais em branco mais em branco. Abaixo de y ao quadrado está a letra F e abaixo de cada espaço em branco estão as letras O, I e L, respectivamente. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os termos externos”. A segunda coluna contém o produto de y menos 7 e y mais 4 novamente, com uma segunda seta se estendendo de y no primeiro binômio até 4 no segundo binômio. A terceira coluna contém y ao quadrado mais 4y mais branco mais branco. Abaixo de y ao quadrado está F, abaixo de 4y está O e abaixo dos espaços em branco estão I e L. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os termos internos”. A coluna do meio contém o produto de y menos 7 e y mais 4 novamente, com uma terceira seta se estendendo do menos 7 no primeiro binômio até o y no segundo binômio. A terceira coluna contém y ao quadrado mais 4y menos 7y mais espaço em branco. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os últimos termos”. A segunda coluna contém o produto de y menos 7 e y mais 4 novamente, com uma quarta seta se estendendo de menos 7 no primeiro binômio até 4 no segundo binômio. Na terceira coluna está a expressão completa, y ao quadrado mais 4y menos 7y menos 28, com cada letra de FOIL abaixo de cada um dos termos. Na parte inferior da imagem, o texto na primeira coluna diz “Combine termos semelhantes”. Na coluna da direita está y ao quadrado menos 3y menos 28.$

Exercício$\PageIndex{35}$

Multiplique:$(x−7)(x+5)$.

Resposta: $x^{2}-2 x-35$

Exercício$\PageIndex{36}$

Multiplique: (b−3) (b+6).

Resposta: $b^{2}+3 b-18$

Exercício$\PageIndex{37}$

Multiplique:$(4x+3)(2x−5)$.

Resposta: $Essa figura tem três colunas. No topo da figura, a segunda coluna contém o produto de dois binômios, 4x mais 3 e 2x menos 5. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os primeiros termos. 4x vezes 2x”. A segunda coluna contém 8x ao quadrado mais branco mais branco mais branco mais branco. Abaixo de 8x ao quadrado está a letra F e abaixo de cada espaço em branco estão as letras O, I e L, respectivamente. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os termos externos. 4x vezes menos 5”. A segunda coluna contém 8x ao quadrado menos 20x mais branco mais espaço em branco. Abaixo de 8x ao quadrado está F, abaixo de 20x está O e abaixo dos espaços em branco estão I e L. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os termos internos. 3 vezes 2x”. A segunda coluna contém 8x ao quadrado menos 20x mais 6x mais espaço em branco. Uma linha abaixo, o texto na primeira coluna diz “Multiplique os últimos termos. 3 vezes menos 5”. A segunda coluna contém a expressão completa, 8x ao quadrado menos 20x mais 6x menos 15, com cada letra de FOIL abaixo de cada um dos termos. Na parte inferior da imagem, o texto na primeira coluna diz “Combine termos semelhantes”. Na coluna da direita está 8x ao quadrado menos 14x menos 15. Na terceira coluna está o produto dos dois binômios novamente, 4x mais 3 vezes 2x menos 5. Uma seta se estende de 4x no primeiro binômio a 2x no segundo binômio. Uma segunda seta se estende de 4x no primeiro binômio até menos 5 no segundo binômio. Uma terceira seta se estende de 3 no primeiro binômio a 2x no segundo binômio. Uma quarta seta se estende de 3 no primeiro binômio a menos 5 no segundo binômio.$

Exercício$\PageIndex{38}$

Multiplique:$(3x+7)(5x−2)$.

Resposta: $15 x^{2}+29 x-14$

Exercício$\PageIndex{39}$

Multiplique:$(4y+5)(4y−10)$.

Resposta: $16 y^{2}-20 y-50$

Os produtos finais nos últimos quatro exemplos foram trinômios porque pudemos combinar os dois termos intermediários. Isso nem sempre é o caso.

Exercício$\PageIndex{40}$

Multiplique:$(3x−y)(2x−5)$.

Resposta

	$(3 x-y)(2 x-5)$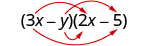
	$Uma seta se estende de 3 x no primeiro binômio a 2 x no segundo binômio. Uma segunda seta se estende de 3 x no primeiro binômio até menos 5 no segundo binômio. Uma terceira seta se estende de y no primeiro binômio até 2 x no segundo binômio. Uma quarta seta se estende de y no primeiro binômio até menos 5 no segundo binômio.$
Multiplique o primeiro.	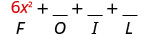$6 x quadrado mais branco mais branco mais branco mais branco. Abaixo de 6 x ao quadrado está a letra F.$
Multiplique o externo.	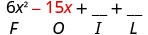$6 x ao quadrado menos 15 x mais branco mais espaço em branco. Abaixo de 15 x está a letra O.$
Multiplique o interno.	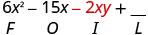$6x ao quadrado menos 15x menos 2xy mais espaço em branco. Abaixo de menos 2 x y está a letra I.$
Multiplique o último.	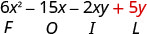$6 x ao quadrado menos 15 x menos 2 x y mais 5 y. Abaixo de 5 y está a letra L.$
Combine termos semelhantes — não há nenhum.	$6 x^{2}-15 x-2 x y+5 y$

Exercício$\PageIndex{41}$

Multiplique: (10c−d) (c−6).

Resposta: $10 c^{2}-60 c-c d+6 d$

Exercício$\PageIndex{42}$

Multiplique: (7x−y) (2x−5).

Resposta: $14 x^{2}-35 x-2 x y+10 y$

Tenha cuidado com os expoentes no próximo exemplo.

Exercício$\PageIndex{43}$

Multiplique:$\left(n^{2}+4\right)(n-1)$

Resposta

	$\left(n^{2}+4\right)(n-1)$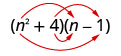
	$O produto de dois binômios, n ao quadrado mais 4 e n menos 1. Uma seta se estende de n ao quadrado no primeiro binômio até n no segundo binômio. Uma segunda seta se estende de n ao quadrado no primeiro binômio até menos 1 no segundo binômio. Uma terceira seta se estende de 4 no primeiro binômio até n no segundo binômio. Uma quarta seta se estende de 4 no primeiro binômio até menos 1 no segundo binômio.$
Multiplique o primeiro.	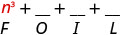$n ao cubo mais em branco mais em branco mais em branco. Abaixo de n ao cubo está a letra F.$
Multiplique o externo.	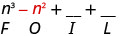$n ao cubo menos n ao quadrado mais branco mais espaço em branco. Abaixo de menos n ao quadrado está a letra O.$
Multiplique o interno.	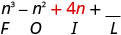$n ao cubo menos n ao quadrado mais 4 n mais espaço em branco. Abaixo de 4 n está a letra I.$
Multiplique o último.	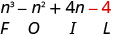$n ao cubo menos n ao quadrado mais 4 n menos 4. Abaixo de menos 4 está a letra L.$
Combine termos semelhantes — não há nenhum.	\ (\ n^ {3} -n^ {2} +4 n-4)

Exercício$\PageIndex{44}$

Multiplique:$\left(x^{2}+6\right)(x-8)$

Resposta: $x^{3}-8 x^{2}+6 x-48$

Exercício$\PageIndex{45}$

Multiplique:$\left(y^{2}+7\right)(y-9)$

Resposta: $y^{3}-9 y^{2}+7 y-63$

Exercício$\PageIndex{46}$

Multiplique:$(3 p q+5)(6 p q-11)$

Resposta

	$(3 p q+5)(6 p q-11)$
Multiplique o primeiro.	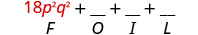$18 p ao quadrado q ao quadrado mais branco mais branco mais branco mais branco. Abaixo de 18 p ao quadrado q ao quadrado está a letra F.$	$O produto de dois binômios, 3 p q mais 5 e 6 p q menos 11. Uma seta se estende de 3 p q no primeiro binômio até 6 p q no segundo binômio. Uma segunda seta se estende de 3 p q no primeiro binômio até menos 11 no segundo binômio. Uma terceira seta se estende de 5 no primeiro binômio a 6 p q no segundo binômio. Uma quarta seta se estende de 5 no primeiro binômio a menos 11 no segundo binômio.$
Multiplique o externo.	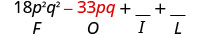$18 p ao quadrado q ao quadrado menos 33 p q mais branco mais espaço em branco. Abaixo de menos 33 p q está a letra O.$
Multiplique o interno.	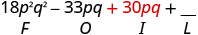$18 p ao quadrado q ao quadrado menos 33 p q mais 30 p q mais espaço em branco. Abaixo de 30 p q está a letra I.$
Multiplique o último.	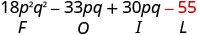$18 p ao quadrado q ao quadrado menos 33 p q mais 30 p q menos 55. Abaixo de menos 55 está a letra L.$
Combine termos semelhantes — não há nenhum.	$18 p^{2} q^{2}-3 p q-55$

Exercício$\PageIndex{47}$

Multiplique:$(2 a b+5)(4 a b-4)$

Resposta: $8 a^{2} b^{2}+12 a b-20$

Exercício$\PageIndex{48}$

Multiplique:$(2 x y+3)(4 x y-5)$

Resposta: $8 x^{2} y^{2}+2 x y-15$

Multiplique um binômio por um binômio usando o método vertical

O método FOIL geralmente é o método mais rápido para multiplicar dois binômios, mas só funciona para binômios. Você pode usar a Propriedade Distributiva para encontrar o produto de quaisquer dois polinômios. Outro método que funciona para todos os polinômios é o Método Vertical. É muito parecido com o método usado para multiplicar números inteiros. Veja cuidadosamente este exemplo de multiplicação de números de dois dígitos.

$Esta figura mostra a multiplicação vertical de 23 e 46. O número 23 está acima do número 46. Abaixo disso, há o produto parcial 138 sobre o produto parcial 92. O produto final está na parte inferior e é 1058. O texto no lado direito da imagem diz “Comece multiplicando 23 por 6 para obter 138. Em seguida, multiplique 23 por 4, alinhando o produto parcial nas colunas corretas. Por último, você adiciona os produtos parciais.”$

Agora vamos aplicar esse mesmo método para multiplicar dois binômios.

Exercício$\PageIndex{49}$

Multiplique usando o método vertical:$(3 y-1)(2 y-6)$

Resposta

Não importa qual binômio fique no topo.

\[\begin{array}{lll}{\text { Multiply } 3 y-1 \text { by }-6 \text { . }}&& \\ {\text { Multiply } 3 y-1 \text { by } 2 y \text { . }}& &\\ \\ &{\qquad\space3 y-1} & \\& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} & \\ &

ParseError: EOF expected (click for details)

Callstack:
    at (Idioma_Portugues/Livro:_Elementary_Algebra_(OpenStax)/06:_Polinômios/6.03:_Multiplicar_polinômios), /content/body/div[4]/div[3]/div[1]/div/dl/dd/p[2]/span/span, line 1, column 3

& \text{partial product} & \\ \text{Add like terms.} &&\text{product} \end{array}\]

Observe que os produtos parciais são iguais aos termos do método FOIL.

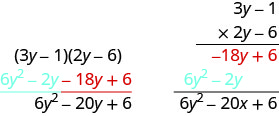
$Essa figura tem duas colunas. Na coluna da esquerda está o produto de dois binômios, 3y menos 1 e 2y menos 6. Abaixo disso está 6y ao quadrado menos 2y menos 18y mais 6. Abaixo disso está 6y ao quadrado menos 20y mais 6. Na coluna da direita está a multiplicação vertical de 3y menos 1 e 2y menos 6. Abaixo disso está o produto parcial negativo 18y mais 6. Abaixo disso está o produto parcial 6y ao quadrado menos 2y. Abaixo disso está 6y ao quadrado menos 20y mais 6.$

Exercício$\PageIndex{50}$

Multiplique usando o método vertical:$(5 m-7)(3 m-6)$

Resposta: $15 m^{2}-51 m+42$

Exercício$\PageIndex{51}$

Multiplique usando o método vertical:$(6 b-5)(7 b-3)$

Resposta: $42 b^{2}-53 b+15$

Agora usamos três métodos para multiplicar binômios. Não deixe de praticar cada método e tente decidir qual deles você prefere. Os métodos estão listados aqui todos juntos, para ajudar você a se lembrar deles.

MULTIPLICAÇÃO DE DOIS BINÔMIOS

Para multiplicar binômios, use:

Propriedade distributiva
Método FOIL
Método vertical

Lembre-se de que o FOIL só funciona ao multiplicar dois binômios.

Multiplique um trinômio por um binômio

Multiplicamos monômios por monômios, monômios por polinômios e binômios por binômios. Agora estamos prontos para multiplicar um trinômio por um binômio. Lembre-se de que FOIL não funcionará nesse caso, mas podemos usar a propriedade distributiva ou o método vertical. Primeiro, examinamos um exemplo usando a propriedade distributiva.

Exercício$\PageIndex{52}$

Multiplique usando a propriedade distributiva:$(b+3)\left(2 b^{2}-5 b+8\right)$

Resposta

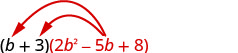
	$O produto de um binômio, b mais 3 e um trinômio, 2 b ao quadrado menos 5 b mais 8. Duas setas se estendem do trinômio, terminando em b e 3 no binômio.$
Distribuir.	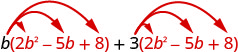$A soma de dois produtos, o produto de b e 2 b ao quadrado menos 5 b mais 8 e o produto de 3 e 2 b ao quadrado menos 5 b mais 8.$
Multiplique.	$2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24$
Combine termos semelhantes.	$2 b^{3}+b^{2}-7 b+24$

Exercício$\PageIndex{53}$

Multiplique usando a propriedade distributiva:$(y-3)\left(y^{2}-5 y+2\right)$

Resposta: $y^{3}-8 y^{2}+17 y-6$

Exercício$\PageIndex{54}$

Multiplique usando a propriedade distributiva:$(x+4)\left(2 x^{2}-3 x+5\right)$

Resposta: $2 x^{3}+5 x^{2}-7 x+20$

Agora vamos fazer essa mesma multiplicação usando o Método Vertical.

Exercício$\PageIndex{55}$

Multiplique usando o método vertical:$(b+3)\left(2 b^{2}-5 b+8\right)$

Resposta

É mais fácil colocar o polinômio com menos termos na parte inferior porque obtemos menos produtos parciais dessa forma.

Multiplique$(2b^2 − 5b + 8)$ por 3.	$.$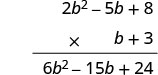
	$.$
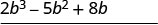
Multiplique$(2b^2 − 5b + 8)$ por$b$.	$2 b^{3}+b^{2}-7 b+24$
Adicione termos semelhantes.

Exercício$\PageIndex{56}$

Multiplique usando o método vertical:$(y-3)\left(y^{2}-5 y+2\right)$

Resposta: $y^{3}-8 y^{2}+17 y-6$

Exercício$\PageIndex{57}$

Multiplique usando o método vertical:$(x+4)\left(2 x^{2}-3 x+5\right)$

Resposta: $2 x^{3}+5 x^{2}-7 x+20$

Agora vimos dois métodos que você pode usar para multiplicar um trinômio por um binômio. Depois de praticar cada método, você provavelmente descobrirá que prefere um método ao outro. Listamos os dois métodos listados aqui, para facilitar a consulta.

MULTIPLICANDO UM TRINÔMIO POR UM BINÔMIO

Para multiplicar um trinômio por um binômio, use:

Propriedade distributiva
Método vertical

Nota

Acesse esses recursos on-line para obter instruções e práticas adicionais com a multiplicação de polinômios:

Multiplicação de expoentes 1
Multiplicação de expoentes 2
Multiplicação de expoentes 3

Conceitos chave

Método FOIL para multiplicação de dois binômios — Para multiplicar dois binômios:
1. Multiplique os primeiros termos.
2. Multiplique os termos externos.
3. Multiplique os termos internos.
4. Multiplique os últimos termos.
Multiplicação de dois binômios — Para multiplicar binômios, use:
- Propriedade distributiva (exemplo)
- Método FOIL (exemplo)
- Método vertical (exemplo)
Multiplicação de um trinômio por um binômio — Para multiplicar um trinômio por um binômio, use:
- Propriedade distributiva (exemplo)
- Método vertical (exemplo)

	$4 vezes x mais 3. Duas setas se estendem de 4, terminando em x e 3.$
Distribuir.	\(4 \cdot x+4 \cdot 3\)
Simplifique.	\(4 x+12\)

	$y vezes y menos 2. Duas setas se estendem do coeficiente y, terminando em y e menos 2 entre parênteses.$
Distribuir.	\(y \cdot y-y \cdot 2\)
Simplifique.	\(y^{2}-2 y\)

	$2 x vezes ao cubo x ao quadrado menos 8 x mais 1. Três setas se estendem de 2 x ao cubo, terminando em x ao quadrado, menos 8 x e 1.$
Distribuir.	\(2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1\)
Simplifique.	\(2 x^{5}-16 x^{4}+2 x^{3}\)

Instruções	Expressão
Expressões iniciais	$x mais 3, entre parênteses, vezes p. Duas setas se estendem do p, terminando em x e 3.$
Distribuímos o\(p\) para obter:	$x p mais 3 p.$
E se tivermos\((x + 7)\) em vez de\(p\)?	$x mais 3 multiplicado por x mais 7. Duas setas se estendem de x mais 7, terminando em x e 3 no primeiro binômio.$
Distribuir\((x + 7)\).	$A soma de dois produtos. O produto de x e x mais 7, mais o produto de 3 e x mais 7.$
Distribua novamente.	\(x^{2}+7 x+3 x+21\)
Combine termos semelhantes.	\(x^{2}+10 x+21\)

	\((3 x-y)(2 x-5)\)
	$Uma seta se estende de 3 x no primeiro binômio a 2 x no segundo binômio. Uma segunda seta se estende de 3 x no primeiro binômio até menos 5 no segundo binômio. Uma terceira seta se estende de y no primeiro binômio até 2 x no segundo binômio. Uma quarta seta se estende de y no primeiro binômio até menos 5 no segundo binômio.$
Multiplique o primeiro.	$6 x quadrado mais branco mais branco mais branco mais branco. Abaixo de 6 x ao quadrado está a letra F.$
Multiplique o externo.	$6 x ao quadrado menos 15 x mais branco mais espaço em branco. Abaixo de 15 x está a letra O.$
Multiplique o interno.	$6x ao quadrado menos 15x menos 2xy mais espaço em branco. Abaixo de menos 2 x y está a letra I.$
Multiplique o último.	$6 x ao quadrado menos 15 x menos 2 x y mais 5 y. Abaixo de 5 y está a letra L.$
Combine termos semelhantes — não há nenhum.	\(6 x^{2}-15 x-2 x y+5 y\)

	\(\left(n^{2}+4\right)(n-1)\)
	$O produto de dois binômios, n ao quadrado mais 4 e n menos 1. Uma seta se estende de n ao quadrado no primeiro binômio até n no segundo binômio. Uma segunda seta se estende de n ao quadrado no primeiro binômio até menos 1 no segundo binômio. Uma terceira seta se estende de 4 no primeiro binômio até n no segundo binômio. Uma quarta seta se estende de 4 no primeiro binômio até menos 1 no segundo binômio.$
Multiplique o primeiro.	$n ao cubo mais em branco mais em branco mais em branco. Abaixo de n ao cubo está a letra F.$
Multiplique o externo.	$n ao cubo menos n ao quadrado mais branco mais espaço em branco. Abaixo de menos n ao quadrado está a letra O.$
Multiplique o interno.	$n ao cubo menos n ao quadrado mais 4 n mais espaço em branco. Abaixo de 4 n está a letra I.$
Multiplique o último.	$n ao cubo menos n ao quadrado mais 4 n menos 4. Abaixo de menos 4 está a letra L.$
Combine termos semelhantes — não há nenhum.	\ (\ n^ {3} -n^ {2} +4 n-4)

	\((3 p q+5)(6 p q-11)\)
Multiplique o primeiro.	$18 p ao quadrado q ao quadrado mais branco mais branco mais branco mais branco. Abaixo de 18 p ao quadrado q ao quadrado está a letra F.$	$O produto de dois binômios, 3 p q mais 5 e 6 p q menos 11. Uma seta se estende de 3 p q no primeiro binômio até 6 p q no segundo binômio. Uma segunda seta se estende de 3 p q no primeiro binômio até menos 11 no segundo binômio. Uma terceira seta se estende de 5 no primeiro binômio a 6 p q no segundo binômio. Uma quarta seta se estende de 5 no primeiro binômio a menos 11 no segundo binômio.$
Multiplique o externo.	$18 p ao quadrado q ao quadrado menos 33 p q mais branco mais espaço em branco. Abaixo de menos 33 p q está a letra O.$
Multiplique o interno.	$18 p ao quadrado q ao quadrado menos 33 p q mais 30 p q mais espaço em branco. Abaixo de 30 p q está a letra I.$
Multiplique o último.	$18 p ao quadrado q ao quadrado menos 33 p q mais 30 p q menos 55. Abaixo de menos 55 está a letra L.$
Combine termos semelhantes — não há nenhum.	\(18 p^{2} q^{2}-3 p q-55\)

Multiplique\((2b^2 − 5b + 8)\) por 3.	$.$
	$.$
Multiplique\((2b^2 − 5b + 8)\) por\(b\).	\(2 b^{3}+b^{2}-7 b+24\)
Adicione termos semelhantes.

Objetivos de

Nota

Multiplique um polinômio por um monômio

Exercício\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)

Exercício\(\PageIndex{4}\)

Exercício\(\PageIndex{5}\)

Exercício\(\PageIndex{6}\)

Exercício\(\PageIndex{7}\)

Exercício\(\PageIndex{8}\)

Exercício\(\PageIndex{9}\)

Exercício\(\PageIndex{10}\)

Exercício\(\PageIndex{11}\)

Exercício\(\PageIndex{12}\)

Exercício\(\PageIndex{13}\)

Exercício\(\PageIndex{14}\)

Exercício\(\PageIndex{15}\)

Exercício\(\PageIndex{16}\)

Exercício\(\PageIndex{17}\)

Exercício\(\PageIndex{18}\)

Multiplique um binômio por um binômio

Multiplique um binômio por um binômio usando a propriedade distributiva

Exercício\(\PageIndex{19}\)

Exercício\(\PageIndex{20}\)

Exercício\(\PageIndex{21}\)

Exercício\(\PageIndex{22}\)

Exercício\(\PageIndex{23}\)

Exercício\(\PageIndex{24}\)

Exercício\(\PageIndex{25}\)

Exercício\(\PageIndex{26}\)

Exercício\(\PageIndex{27}\)

Exercício\(\PageIndex{28}\)

Exercício\(\PageIndex{29}\)

Exercício\(\PageIndex{30}\)

Multiplique um binômio por um binômio usando o método FOIL

Exercício\(\PageIndex{31}\): How to Multiply a Binomial by a Binomial using the FOIL Method

Exercício\(\PageIndex{32}\)

Exercício\(\PageIndex{33}\)

MULTIPLIQUE DOIS BINÔMIOS USANDO O MÉTODO FOIL

Exercício\(\PageIndex{34}\)

Exercício\(\PageIndex{35}\)

Exercício\(\PageIndex{36}\)

Exercício\(\PageIndex{37}\)

Exercício\(\PageIndex{38}\)

Exercício\(\PageIndex{39}\)

Exercício\(\PageIndex{40}\)

Exercício\(\PageIndex{41}\)

Exercício\(\PageIndex{42}\)

Exercício\(\PageIndex{43}\)

Exercício\(\PageIndex{44}\)

Exercício\(\PageIndex{45}\)

Exercício\(\PageIndex{46}\)

Exercício\(\PageIndex{47}\)

Exercício\(\PageIndex{48}\)

Multiplique um binômio por um binômio usando o método vertical

Exercício\(\PageIndex{49}\)

Exercício\(\PageIndex{50}\)

Exercício\(\PageIndex{51}\)

MULTIPLICAÇÃO DE DOIS BINÔMIOS

Multiplique um trinômio por um binômio

Exercício\(\PageIndex{52}\)

Exercício\(\PageIndex{53}\)

Exercício\(\PageIndex{54}\)

Exercício\(\PageIndex{55}\)

Exercício\(\PageIndex{56}\)

Exercício\(\PageIndex{57}\)

MULTIPLICANDO UM TRINÔMIO POR UM BINÔMIO

Nota

Conceitos chave