Skip to main content
Global

4.7: Gráficos de desigualdades lineares

  1. Last updated
  2. Save as PDF
  • Page ID
    184224

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Verificar soluções para uma desigualdade em duas variáveis
    • Reconhecer a relação entre as soluções de uma desigualdade e seu gráfico
    • Gráfico de desigualdades lineares
    Nota

    Antes de começar, faça este teste de prontidão.

    1. Solução:\(4x+3>23.\)
      Se você perdeu esse problema, revise o Exercício 2.7.22.
    2. Traduzir da álgebra para o inglês:\(x<5.\)
      Se você perdeu esse problema, revise o Exercício 1.3.1.
    3. Avalie\(3x−2y\) quando\(x=1, \, y=−2.\)
      se esqueceu desse problema, revise o Exercício 1.5.28.

    Verificar soluções para uma desigualdade em duas variáveis

    Aprendemos como resolver desigualdades em uma variável. Agora, veremos as desigualdades em duas variáveis. As desigualdades em duas variáveis têm muitas aplicações. Se você dirigisse uma empresa, por exemplo, gostaria que sua receita fosse maior do que seus custos, para que sua empresa gerasse lucro.

    DESEQUAÇÃO LINEAR

    Uma desigualdade linear é uma desigualdade que pode ser escrita em uma das seguintes formas:

    \[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]

    onde\(A\) e não\(B\) são ambos zero.

    Você se lembra que uma desigualdade com uma variável tinha muitas soluções? A solução para a desigualdade\(x>3\) é qualquer número maior que\(3\). Mostramos isso na reta numérica sombreando a reta numérica à direita de\(3\) e colocando um parêntese aberto em\(3\). Veja a Figura\(\PageIndex{1}\).

    A figura mostra uma reta numérica que se estende de menos 5 a 5. Um parêntese é mostrado em positivo 3 e uma seta se estende do positivo 3 até o infinito positivo.
    Figura\(\PageIndex{1}\)

    Da mesma forma, as desigualdades em duas variáveis têm muitas soluções. Qualquer par ordenado\( (x, y)\) que torne a desigualdade verdadeira quando substituímos os valores é uma solução da desigualdade.

    SOLUÇÃO DE UMA DESIGUALDADE LINEAR

    Um par ordenado\( (x, y)\) é uma solução de uma desigualdade linear se a desigualdade for verdadeira quando substituímos os valores de\(x\)\(y\) e.

    Exercício\(\PageIndex{1}\)

    Determine se cada par ordenado é uma solução para a desigualdade\(y>x+4\):

    1. \((0,0)\)
    2. \((1,6)\)
    3. \((2,6)\)
    4. \((−5,−15)\)
    5. \((−8,12)\)
    Resposta
    1.
    \((0,0)\) .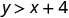
    . .
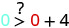
    Simplifique. .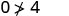
    Então, não\((0,0)\) é uma solução para\(y>x+4\).
    2.
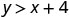
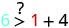
    \((1,6)\) .
    . .
    Simplifique. .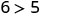
    Então,\((1,6)\) é uma solução para\(y>x+4\).
    3.
    \((2,6)\) .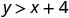
    . .
    Simplifique. .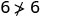
    Então, não\((2,6)\) é uma solução para\(y>x+4\).
    4.
    \((−5,−15)\) .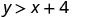
    . .
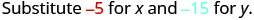
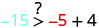
    Simplifique. .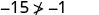
    Então, não\((−5,−15)\) é uma solução para\(y>x+4\).
    5.
    (−8,12) .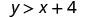
    . .
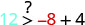
    Simplifique. .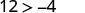
    Então,\((−8,12)\) é uma solução para\(y>x+4\).
    Exercício\(\PageIndex{2}\)

    Determine se cada par ordenado é uma solução para a desigualdade\(y>x−3\):

    1. \((0,0)\)
    2. \((4,9)\)
    3. \((−2,1)\)
    4. \((−5,−3)\)
    5. \((5,1)\)
    Resposta
    1. sim
    2. sim
    3. sim
    4. sim
    5. não
    Exercício\(\PageIndex{3}\)

    Determine se cada par ordenado é uma solução para a desigualdade\(y<x+1\):

    1. \((0,0)\)
    2. \((8,6)\)
    3. \((−2,−1)\)
    4. \((3,4)\)
    5. \((−1,−4)\)
    Resposta
    1. sim
    2. sim
    3. não
    4. não
    5. sim

    Reconhecer a relação entre as soluções de uma desigualdade e seu gráfico

    Agora, veremos como as soluções de uma desigualdade se relacionam com seu gráfico.

    Vamos pensar na reta numérica na Figura\(\PageIndex{1}\) novamente. O ponto\(x=3\) separou essa reta numérica em duas partes. De um lado de\(3\) estão todos os números menores que\(3\). No outro lado de\(3\) todos os números são maiores que\(3\). Veja a Figura\(\PageIndex{2}\).

    A figura mostra uma reta numérica que se estende de menos 5 a 5. Um parêntese é mostrado em positivo 3 e uma seta se estende do positivo 3 até o infinito positivo. Uma seta acima da linha numérica se estende de 3 e aponta para a esquerda. É rotulado como “números menores que 3”. Uma seta acima da linha numérica se estende de 3 e aponta para a direita. É rotulado como “números maiores que 3”.
    Figura\(\PageIndex{2}\)

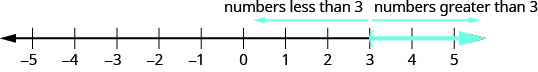
    A solução para\(x>3\) é a parte sombreada da linha numérica à direita de\(x=3\).

    Da mesma forma, a linha\(y=x+4\) separa o plano em duas regiões. Em um lado da linha estão os pontos com\(y<x+4\). Do outro lado da linha estão os pontos com\(y>x+4\). Chamamos a linha\(y=x+4\) de linha limite.

    LINHA LIMITE

    A linha com equação\(Ax+By=C\) é a linha limite que separa a região onde\(Ax+By>C\) da região onde\(Ax+By<C\).

    Para uma desigualdade em uma variável, o ponto final é mostrado com um parêntese ou um colchete, dependendo de aa estar ou não incluído na solução:

    A figura mostra duas linhas numéricas. A linha numérica à esquerda é rotulada como x é menor que a. A linha numérica mostra um parêntese em a e uma seta que aponta para a esquerda. A linha numérica à direita é rotulada como x é menor ou igual a a. A linha numérica mostra um colchete em a e uma seta que aponta para a esquerda.

    Da mesma forma, para uma desigualdade em duas variáveis, a linha limite é mostrada com uma linha sólida ou tracejada para indicar se a linha está ou não incluída na solução. Isso está resumido na Tabela\(\PageIndex{1}\).

    \(Ax+By<C\) \(Ax+By\leq C\)
    \(Ax+By>C\) \(Ax+By\geq C\)
    A linha limite não está incluída na solução. A linha limite está incluída na solução.
    A linha limite é tracejada. A linha limite é sólida.
    Tabela\(\PageIndex{1}\)

    Agora, vamos dar uma olhada no que encontramos no Exercício\(\PageIndex{1}\). Começaremos representando graficamente a linha e\(y=x+4\), em seguida, traçaremos os cinco pontos que testamos. Veja a Figura\(\PageIndex{3}\).

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a x mais 4 é traçada como uma seta que se estende do canto inferior esquerdo em direção ao canto superior direito. Os pontos a seguir são plotados e rotulados (menos 8, 12), (1, 6), (2, 6), (0, 0) e (menos 5, menos 15).
    Figura\(\PageIndex{3}\)

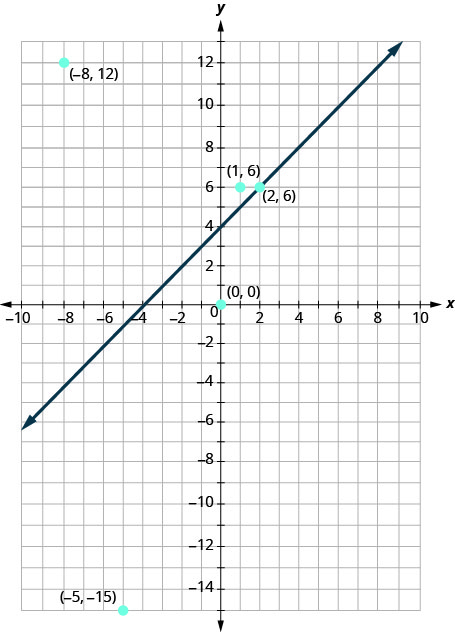
    No Exercício,\(\PageIndex{1}\) descobrimos que alguns dos pontos eram soluções para a desigualdade\(y>x+4\) e outros não.

    Quais dos pontos traçados são soluções para a desigualdade\(y>x+4\)? Os pontos\((1,6)\) e\((−8,12)\) são soluções para a desigualdade\(y>x+4\). Observe que ambos estão do mesmo lado da linha limite\(y=x+4\).

    Os dois pontos\((0,0)\)\((−5,−15)\) estão do outro lado da linha\(y=x+4\) limite e não são soluções para a desigualdade\(y>x+4\). Para esses dois pontos,\(y<x+4\).

    E quanto ao ponto\((2,6)\)? Porque\(6=2+4\) o ponto é uma solução para a equação\(y=x+4\). Portanto, o ponto\((2,6)\) está na linha limite.

    Vamos pegar outro ponto no lado esquerdo da linha limite e testar se é ou não uma solução para a desigualdade\(y>x+4\). O ponto\((0,10)\) claramente parece estar à esquerda da linha limite, não é? É uma solução para a desigualdade?

    \[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]

    Qualquer ponto escolhido no lado esquerdo da linha limite é uma solução para a desigualdade\(y>x+4\). Todos os pontos à esquerda são soluções.

    Da mesma forma, todos os pontos no lado direito da linha limite, o lado com\((0,0)\) e\((−5,−15)\), não são soluções para\(y>x+4\). Veja a Figura\(\PageIndex{4}\).

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a x mais 4 é traçada como uma seta que se estende do canto inferior esquerdo em direção ao canto superior direito. Os pontos a seguir são plotados e rotulados (menos 8, 12), (1, 6), (2, 6), (0, 0) e (menos 5, menos 15). No canto superior esquerdo da linha está a desigualdade y é maior que x mais 4. À direita da linha está a desigualdade y é menor que x mais 4.
    Figura\(\PageIndex{4}\)

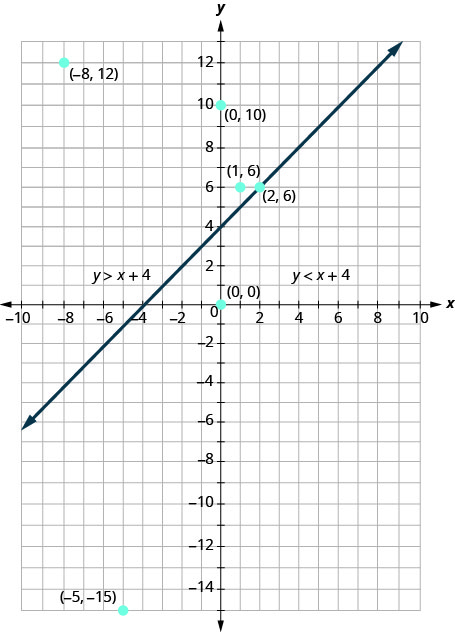
    O gráfico da desigualdade\(y>x+4\) é mostrado na Figura\(\PageIndex{5}\) abaixo. A linha\(y=x+4\) divide o plano em duas regiões. O lado sombreado mostra as soluções para a desigualdade\(y>x+4\).

    Os pontos na linha limite, aqueles em que\(y=x+4\), não são soluções para a desigualdade\(y>x+4\), então a linha em si não faz parte da solução. Mostramos isso tornando a linha tracejada, não sólida.

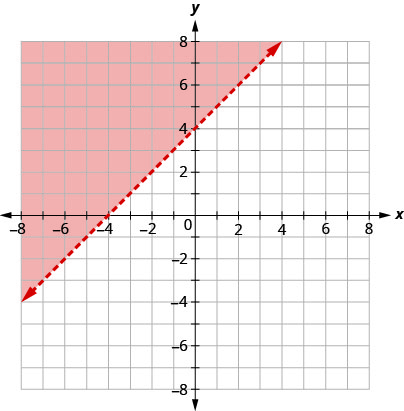
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a x mais 4 é traçada como uma seta tracejada que se estende do canto inferior esquerdo em direção ao canto superior direito. O plano de coordenadas no canto superior esquerdo da linha está sombreado.
    Figura\(\PageIndex{5}\): O gráfico da desigualdade y>x+4.
    Exercício\(\PageIndex{4}\)

    A linha limite mostrada é\(y=2x−1\). Escreva a desigualdade mostrada pelo gráfico.

    Resposta

    A linha\(y=2x−1\) é a linha limite. De um lado da linha estão os pontos com\(y>2x−1\) e do outro lado da linha estão os pontos com\(y<2x−1\).

    Vamos testar o ponto\((0,0)\) e ver qual desigualdade descreve seu lado da linha limite.

    Em\((0,0)\), qual desigualdade é verdadeira:

    \[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]

    Como\(y>2x−1\) é verdade, o lado da linha com\((0,0)\), é a solução. A região sombreada mostra a solução da desigualdade\(y>2x−1\).

    Como a linha limite é representada graficamente com uma linha sólida, a desigualdade inclui o sinal de igual.

    O gráfico mostra a desigualdade\(y\geq 2x−1\).

    Podemos usar qualquer ponto como ponto de teste, desde que não esteja na linha. Por que escolhemos\((0,0)\)? Porque é o mais fácil de avaliar. Talvez você queira escolher um ponto do outro lado da linha limite e verificar isso\(y<2x−1\).

    Exercício\(\PageIndex{5}\)

    Escreva a desigualdade mostrada pelo gráfico com a linha limite\(y=−2x+3\).

    Resposta

    \(y\geq −2x+3\)

    Exercício\(\PageIndex{6}\)

    Escreva a desigualdade mostrada pelo gráfico com a linha limite\(y=\frac{1}{2}x−4\).

    Resposta

    \(y \leq \frac{1}{2}x - 4\)

    Exercício\(\PageIndex{7}\)

    A linha limite mostrada é\(2x+3y=6\). Escreva a desigualdade mostrada pelo gráfico.

    Responda

    A linha\(2x+3y=6\) é a linha limite. De um lado da linha estão os pontos com\(2x+3y>6\) e do outro lado da linha estão os pontos com\(2x+3y<6\).

    Vamos testar o ponto\((0,0)\) e ver qual desigualdade descreve seu lado da linha limite.

    Em\((0,0)\), qual desigualdade é verdadeira:

    \[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]

    Então, o lado com\((0,0)\) é o lado onde\(2x+3y<6\).

    (Talvez você queira escolher um ponto do outro lado da linha limite e verificar isso\(2x+3y>6\).)

    Como a linha limite é representada graficamente como uma linha tracejada, a desigualdade não inclui um sinal de igual.

    O gráfico mostra a solução para a desigualdade\(2x+3y<6\).

    Exercício\(\PageIndex{8}\)

    Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite\(x−4y=8\).

    Responda

    \(x-4 y \leq 8\)

    Exercício\(\PageIndex{9}\)

    Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite\(3x−y=6\).

    Responda

    \(3 x-y \leq 6\)

    Gráfico de desigualdades lineares

    Agora, estamos prontos para juntar tudo isso para representar graficamente as desigualdades lineares.

    Exercício\(\PageIndex{10}\): How to Graph Linear Inequalities

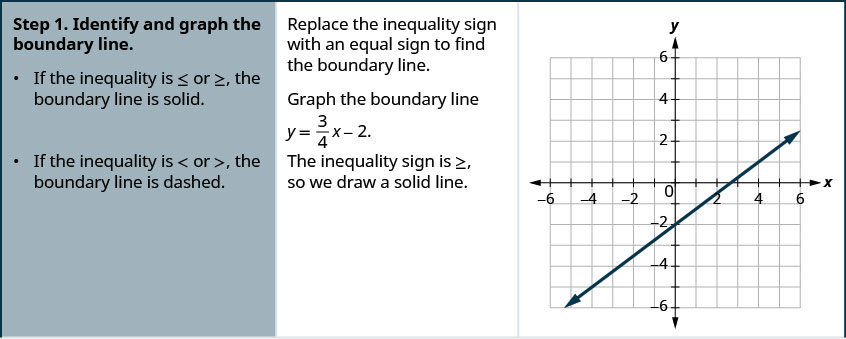
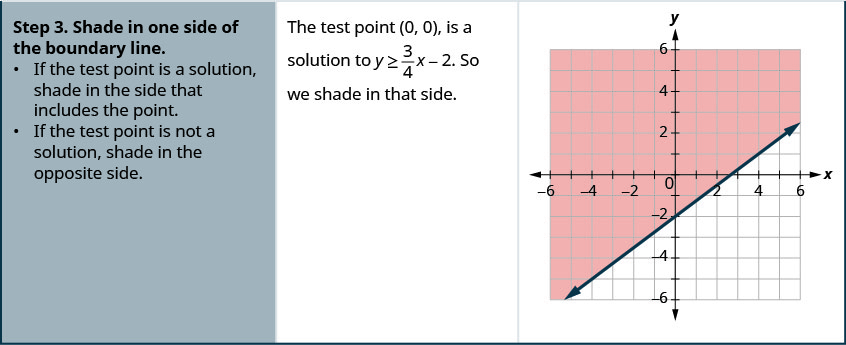
    Representar graficamente a desigualdade linear\(y \geq \frac{3}{4} x-2\).

    Responda

    Essa figura é uma tabela que tem três colunas e três linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda coluna contém mais instruções escritas. A terceira coluna contém matemática. Na linha superior da tabela, a primeira célula à esquerda diz: “Etapa 1. Identifique e represente graficamente a linha limite. Se a desigualdade for menor ou igual ou maior ou igual a, a linha limite será sólida. Se a desigualdade for menor ou maior que, a linha limite será tracejada. O texto na segunda célula diz: “Substitua o sinal de desigualdade por um sinal de igual para encontrar a linha limite. Faça um gráfico da linha limite y é igual a três quartos x menos 2. O sinal de desigualdade é maior ou igual a, então desenhamos uma linha sólida. A terceira célula contém o gráfico da linha três quartos x menos 2 em um plano coordenado.Na segunda linha da tabela, a primeira célula diz: “Etapa 2. Teste um ponto que não esteja na linha limite. É uma solução da desigualdade? Na segunda célula, as instruções dizem: “Vamos testar (0, 0). É uma solução da desigualdade?” A terceira célula pergunta: Em (0, 0), y é maior ou igual a três quartos x menos 2? Abaixo disso, a desigualdade 0 é maior ou igual a três quartos 0 menos 2, com um ponto de interrogação acima do símbolo de desigualdade. Abaixo disso, a desigualdade 0 é maior ou igual a menos 2. Abaixo disso está: “Então (0, 0) é uma solução.Na terceira linha da tabela, a primeira célula diz: “Etapa 3. Sombreie em um lado da linha limite. Se o ponto de teste for uma solução, sombreie o lado que inclui o ponto. Se o ponto de teste não for uma solução, sombreie no lado oposto. Na segunda célula, as instruções dizem: O ponto de teste (0, 0) é uma solução para y maior ou igual a três quartos x menos 2. Então, sombreamos esse lado.” Na terceira célula está o gráfico da linha três quartos x menos 2 em um plano coordenado com a região acima da linha sombreada.

    Exercício\(\PageIndex{11}\)

    Representar graficamente a desigualdade linear\(y \geq \frac{5}{2} x-4\).

    Responda

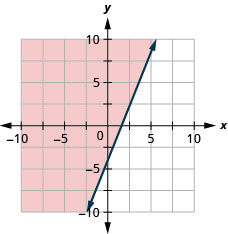
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y é igual a cinco metades x menos 4 é traçada como uma seta sólida que se estende do canto inferior esquerdo em direção ao canto superior direito. A região acima da linha está sombreada.

    Exercício\(\PageIndex{12}\)

    Representar graficamente a desigualdade linear\(y<\frac{2}{3} x-5\).

    Responda

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a dois terços x menos 5 é traçada como uma seta tracejada que se estende do canto inferior esquerdo em direção ao canto superior direito. A região abaixo da linha está sombreada.

    As etapas que tomamos para representar graficamente uma desigualdade linear estão resumidas aqui.

    FAÇA UM GRÁFICO DE UMA DESIGUALDADE LIN
    1. Identifique e represente graficamente a linha limite.
      • Se a desigualdade for\(≤\) ou\(≥\), a linha limite será sólida.
      • Se a desigualdade for\(<\) ou\(>\), a linha limite será tracejada.
    2. Teste um ponto que não esteja na linha limite. É uma solução da desigualdade?
    3. Sombreie em um lado da linha limite.
      • Se o ponto de teste for uma solução, sombreie o lado que inclui o ponto.
      • Se o ponto de teste não for uma solução, sombreie no lado oposto.
    Exercício\(\PageIndex{13}\)

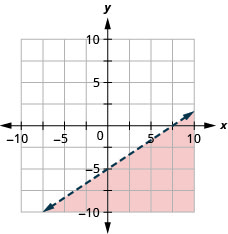
    Representar graficamente a desigualdade linear\(x−2y<5\).

    Responda

    Primeiro, representamos graficamente a linha limite\(x−2y=5\). A desigualdade é\(<\) então que desenhamos uma linha tracejada.

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha x menos 2 y é igual a 5 é traçada como uma seta tracejada que se estende do canto inferior esquerdo em direção ao canto superior direito.

    Em seguida, testamos um ponto. Usaremos\((0,0)\) novamente porque é fácil de avaliar e não está na linha limite.

    É\((0,0)\) uma solução de\(x−2y<5\)?

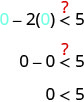
    A figura mostra que a desigualdade 0 menos 2 vezes 0 entre parênteses é menor que 5, com um ponto de interrogação acima do símbolo de desigualdade. A próxima linha mostra que 0 menos 0 é menor que 5, com um ponto de interrogação acima do símbolo de desigualdade. A terceira linha mostra que 0 é menor que 5.

    O ponto\((0,0)\) é uma solução de\(x−2y<5\), então sombreamos esse lado da linha limite.

    Exercício\(\PageIndex{14}\)

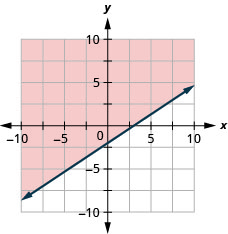
    Representar graficamente a desigualdade linear\(2x−3y\leq 6\).

    Responda

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha 2 x menos 3 y é igual a 6 é traçada como uma seta sólida que se estende do canto inferior esquerdo em direção ao canto superior direito. A região acima da linha está sombreada.

    Exercício\(\PageIndex{15}\)

    Representar graficamente a desigualdade linear\(2x−y>3\).

    Responda

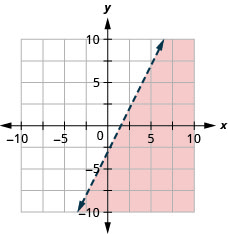
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha 2 x menos y é igual a 3 é traçada como uma seta tracejada que se estende do canto inferior esquerdo em direção ao canto superior direito. A região abaixo da linha está sombreada.

    E se a linha limite passar pela origem? Então, não poderemos usar\((0,0)\) como ponto de teste. Sem problemas, vamos apenas escolher outro ponto que não esteja na linha limite.

    Exercício\(\PageIndex{16}\)

    Representar graficamente a desigualdade linear\(y\leq −4x\).

    Responda

    Primeiro, representamos graficamente a linha limite\(y=−4x\). Está na forma de inclinação-intercepto, com\(m=−4\)\(b=0\) e. A desigualdade é\(≤\) então que traçamos uma linha sólida.

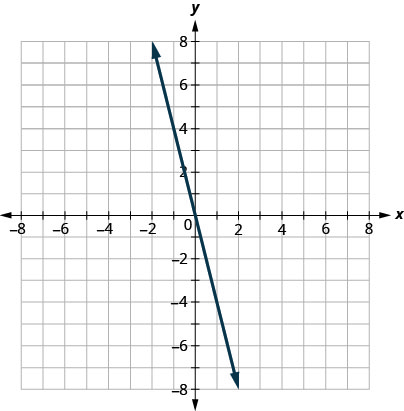
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha s y igual a menos 4 x é traçada como uma seta sólida que se estende do canto superior esquerdo em direção ao canto inferior direito.

    Agora, precisamos de um ponto de teste. Podemos ver que o ponto não\((1,0)\) está na linha limite.

    É\((1,0)\) uma solução de\(y≤−4x\)?

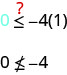
    A figura mostra que 0 é menor ou igual a menos 4 vezes 1 entre parênteses, com um ponto de interrogação acima do símbolo de desigualdade. A próxima linha mostra que 0 não é menor ou igual a menos 4.

    O ponto não\((1,0)\) é uma solução\(y≤−4x\), então sombreamos no lado oposto da linha limite. Veja a Figura\(\PageIndex{6}\).

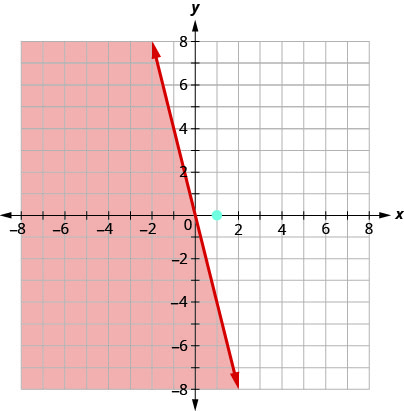
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a menos 4 x é traçada como uma seta sólida que se estende do canto superior esquerdo em direção ao canto inferior direito. O ponto (1, 0) é plotado, mas não rotulado. A região à esquerda da linha está sombreada.
    Figura\(\PageIndex{6}\)
    Exercício\(\PageIndex{17}\)

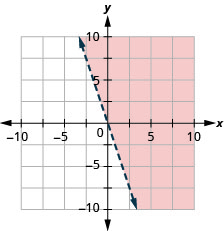
    Representar graficamente a desigualdade linear\(y>−3x\).

    Responda

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a menos 3 x é traçada como uma seta tracejada que se estende do canto superior esquerdo em direção ao canto inferior direito. A região à direita da linha está sombreada.

    Exercício\(\PageIndex{18}\)

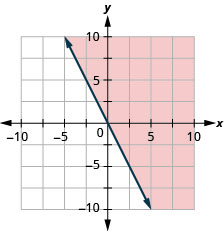
    Representar graficamente a desigualdade linear\(y\geq −2x\).

    Responda

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a menos 2 x é traçada como uma seta sólida que se estende do canto superior esquerdo em direção ao canto inferior direito. A região à direita da linha está sombreada.

    Algumas desigualdades lineares têm apenas uma variável. Eles podem ter um\(x\) mas não\(y\), ou um\(y\) mas não\(x\). Nesses casos, a linha limite será vertical ou horizontal. Você se lembra?

    \(\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}\)

    Exercício\(\PageIndex{19}\)

    Representar graficamente a desigualdade linear\(y>3\).

    Responda

    Primeiro, representamos graficamente a linha limite\(y=3\). É uma linha horizontal. A desigualdade é\(>\) então que desenhamos uma linha tracejada.

    Nós testamos o ponto\((0,0)\).

    \[y>3 \\ 0\not>3\]

    \((0,0)\)não é uma solução para\(y>3\).

    Então, sombreamos o lado que não inclui\((0,0)\).

    Exercício\(\PageIndex{20}\)

    Representar graficamente a desigualdade linear\(y<5\).

    Responda

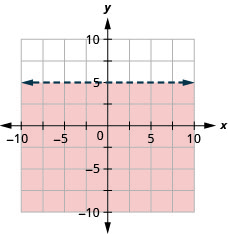
    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a 5 é traçada como uma seta tracejada horizontalmente sobre o plano. A região acima da linha está sombreada.

    Exercício\(\PageIndex{21}\)

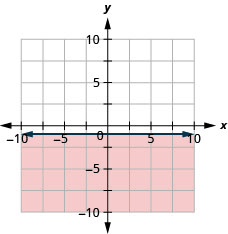
    Representar graficamente a desigualdade linear\(y \leq-1\).

    Responda

    O gráfico mostra o plano da coordenada x y. Cada um dos eixos x e y vai de menos 10 a 10. A linha y igual a menos 1 é traçada como uma seta tracejada horizontalmente no plano. A região abaixo da linha está sombreada.

    Conceitos chave

    • Para representar graficamente uma desigualdade linear
      1. Identifique e represente graficamente a linha limite.
        Se a desigualdade for\(≤\) ou\(≥\), a linha limite será sólida.
        Se a desigualdade for\(<\) ou\(>\), a linha limite será tracejada.
      2. Teste um ponto que não esteja na linha limite. É uma solução da desigualdade?
      3. Sombreie em um lado da linha limite.
        Se o ponto de teste for uma solução, sombreie o lado que inclui o ponto.
        Se o ponto de teste não for uma solução, sombreie no lado oposto.

    Glossário

    linha limite
    A linha com equação\(A x+B y=C\) que separa a região onde\(A x+B y>C\) da região onde\(A x+B y<C\).
    desigualdade linear
    Uma desigualdade que pode ser escrita em uma das seguintes formas:

    \[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]

    onde\(A\) e não\(B\) são ambos zero.
    solução de uma desigualdade linear
    Um par ordenado\((x,\,y)\) é uma solução para uma desigualdade linear; a desigualdade é verdadeira quando substituímos os valores de\(x\)\(y\) e.