4.5: Use a forma inclinação-interceptação de uma equação de uma reta
- Page ID
- 184201
Ao final desta seção, você poderá:
- Reconhecer a relação entre o gráfico e a forma inclinada-interceptação de uma equação de uma reta
- Identifique a inclinação e a forma de intercepto y de uma equação de uma reta
- Faça um gráfico de uma linha usando sua inclinação e intercepte
- Escolha o método mais conveniente para representar graficamente uma linha
- Represente graficamente e interprete aplicações de inclinação-interceptação
- Use inclinações para identificar linhas paralelas
- Use inclinações para identificar linhas perpendiculares
Antes de começar, faça este teste de prontidão.
- Adicionar:\(\frac{x}{4} + \frac{1}{4}\).
Se você perdeu esse problema, revise o Exercício 1.7.1. - Encontre o recíproco de\(\frac{3}{7}\).
Se você perdeu esse problema, revise o Exercício 1.6.19. - Resolver\(2x−3y=12\) para\(y\).
Se você perdeu esse problema, revise o Exercício 2.6.16.
Reconhecer a relação entre o gráfico e a forma inclinada-interceptação de uma equação de uma reta
Representamos graficamente equações lineares traçando pontos, usando interceptações, reconhecendo linhas horizontais e verticais e usando o método ponto-inclinação. Depois de vermos como uma equação na forma de inclinação-intercepto e seu gráfico estão relacionados, teremos mais um método que podemos usar para representar graficamente linhas.
No gráfico de equações lineares em duas variáveis, representamos graficamente a linha da equação\(y=12x+3\) traçando pontos. Veja a Figura\(\PageIndex{1}\). Vamos encontrar a inclinação dessa linha.
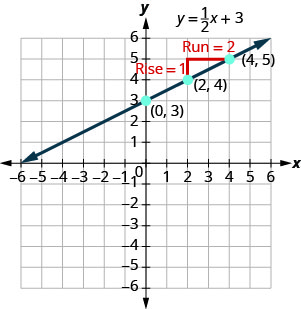
As linhas vermelhas nos mostram que a ascensão é\(1\) e a corrida é\(2\). Substituindo na fórmula da inclinação:
\[\begin{aligned} m &=\frac{\text { rise }}{\text { rise }} \\ m &=\frac{1}{2} \end{aligned}\]
O que é a\(y\) intercepção -da linha? O\(y\) -intercept é onde a linha cruza o\(y\) eixo -, então\(y\) -intercept está\((0,3)\). A equação dessa linha é:
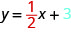
Observe que a linha tem:

Quando uma equação linear é resolvida\(y\), o coeficiente do\(x\) termo -é a inclinação e o termo constante é a\(y\) coordenada\(y\) -do intercepto. Dizemos que a equação\(y=\frac{1}{2}x+3\) está na forma de inclinação-intercepto.
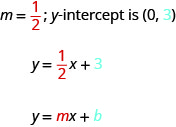
A forma inclinação-interceptação de uma equação de uma reta com inclinação mm e\(y\) -intercepto,\((0,b)\) é,
\[y=mx+b\]
Às vezes, a forma inclinação-intercepto é chamada de “forma y”.
Use o gráfico para encontrar a inclinação e a\(y\) interceptação da linha,\(y=2x+1\).
Compare esses valores com a equação\(y=mx+b\).
- Resposta
-
Para encontrar a inclinação da linha, precisamos escolher dois pontos na linha. Usaremos os pontos\((0,1)\)\((1,3)\) e.
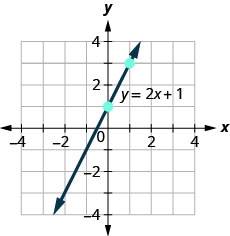
Encontre a ascensão e corra. 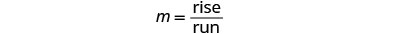
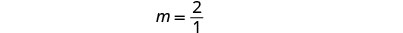
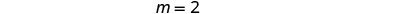
Encontre o\(y\) intercepto -da linha. O\(y\) intercepto -é o ponto\((0, 1)\). 
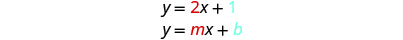
A inclinação é igual ao coeficiente de\(x\) e a\(y\) coordenada -do\(y\) intercepto -é a mesma do termo constante.
Use o gráfico para encontrar a inclinação e a\(y\) interceptação da linha\(y=\frac{2}{3}x−1\). Compare esses valores com a equação\(y=mx+b\).
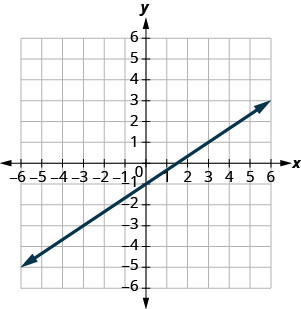
- Resposta
-
inclinação\(m = \frac{2}{3}\) e\(y\) interceptação\((0,−1)\)
Use o gráfico para encontrar a inclinação e a\(y\) interceptação da linha\(y=\frac{1}{2}x+3\). Compare esses valores com a equação\(y=mx+b\).
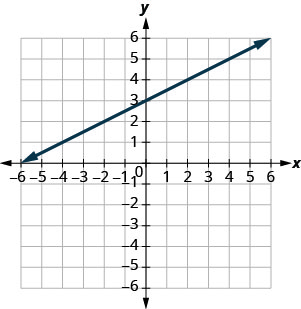
- Resposta
-
inclinação\(m = \frac{1}{2}\) e\(y\) interceptação\((0,3)\)
Identifique a inclinação e a\(y\) interceptação de uma equação de uma reta
Em Entender a[1] inclinação de uma linha, representamos graficamente uma linha usando a inclinação e um ponto. Quando recebemos uma equação na forma inclinação-intercepto, podemos usar o\(y\) intercepto -como ponto e, em seguida, contar a inclinação a partir daí. Vamos praticar a determinação dos valores da inclinação e da\(y\) interceptação a partir da equação de uma reta.
Identifique a inclinação e a\(y\) interceptação da linha com a equação\(y=−3x+5\).
- Resposta
-
Comparamos nossa equação com a forma inclinada-interceptação da equação.
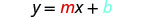
Escreva a equação da linha. 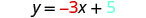
Identifique a inclinação. 
Identifique o\(y\) intercepto. 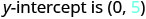
Identifique a inclinação e a\(y\) interceptação da linha\(y=\frac{2}{5}x−1\).
- Resposta
-
\(\frac{2}{5}\); (0, −1)
Identifique a inclinação e a\(y\) interceptação da linha\(y=−\frac{4}{3}x+1\).
- Resposta
-
\(-\frac{4}{3}\); (0,1)
Quando uma equação de uma reta não é dada na forma de inclinação-intercepto, nosso primeiro passo será resolver a equação para\(y\).
Identifique a inclinação e a\(y\) interceptação da linha com a equação\(x+2y=6\).
- Resposta
-
Essa equação não está na forma de inclinação-intercepto. Para compará-la com a forma inclinação-interceptação, devemos primeiro resolver a equação para\(y\).
Resolva para\(y\). \(x+2y=6\) Subtraia x de cada lado. 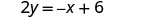
Divida os dois lados por\(2\). 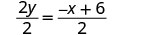
Simplifique. 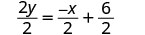
(Lembre-se:\(\frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}\)) Simplifique. 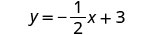
Escreva a forma inclinação-interceptação da equação da reta. 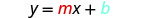
Escreva a equação da linha. 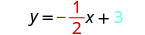
Identifique a inclinação. 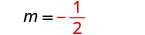
Identifique o\(y\) intercepto. 
Identifique a inclinação e a\(y\) interceptação da linha\(x+4y=8\).
- Resposta
-
\(-\frac{1}{4}\);( 0,2)
Identifique a inclinação e a\(y\) interceptação da linha\(3x+2y=12\).
- Resposta
-
\(-\frac{2}{3}\);( 0,6)
Representar graficamente uma linha usando sua inclinação e interceptação
Agora que sabemos como encontrar a inclinação e a\(y\) interceptação de uma reta a partir de sua equação, podemos representar graficamente a linha traçando o\(y\) intercepto -e, em seguida, usando a inclinação para encontrar outro ponto.
Faça um gráfico da linha da equação\(y=4x−2\) usando sua inclinação e\(y\) intercepto.
- Resposta
-



Faça um gráfico da linha da equação\(y=4x+1\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
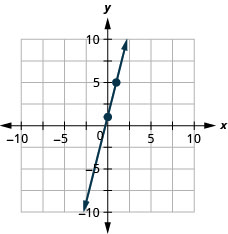
Faça um gráfico da linha da equação\(y=2x−3\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
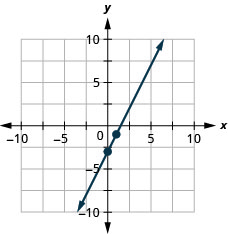
- Encontre a forma de interceptação de inclinação da equação da reta.
- Identifique a inclinação e a\(y\) interceptação.
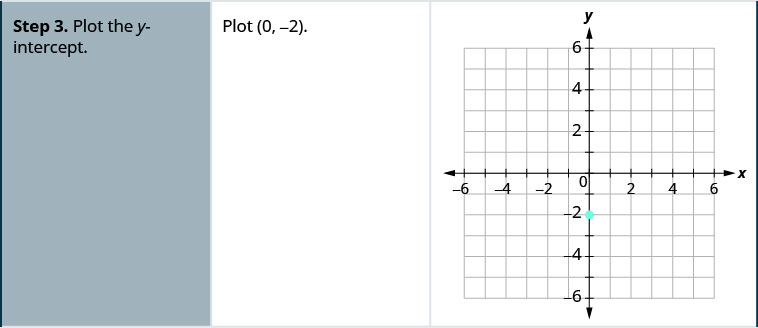
- Faça um gráfico do\(y\) -intercept.
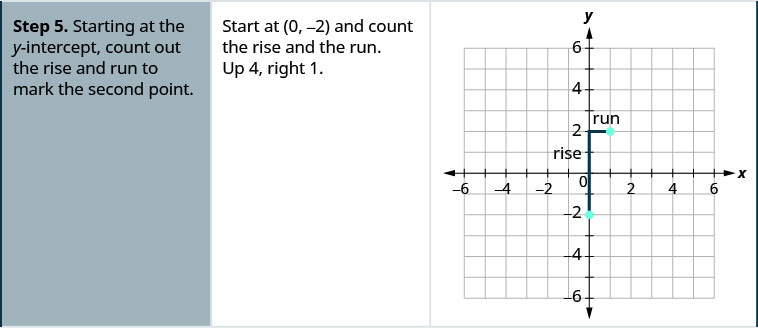
- Use a fórmula da inclinação\(\frac{\text{rise}}{\text{run}}\) para identificar a subida e a corrida.
- Começando na\(y\) interceptação -, conte a subida e corra para marcar o segundo ponto.
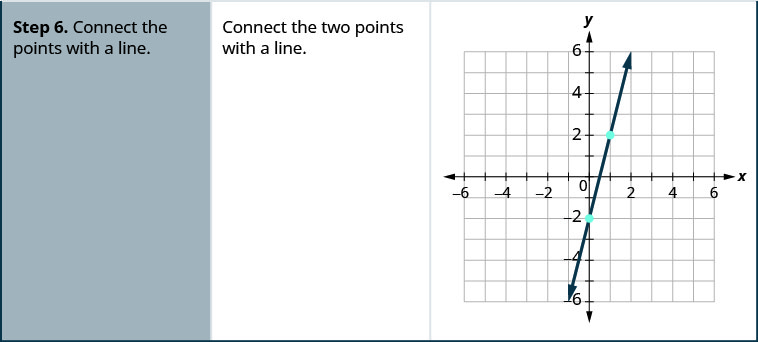
- Conecte os pontos com uma linha.
Faça um gráfico da linha da equação\(y=−x+4\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
cheque.\(y=mx+b\) A equação está na forma de inclinação-interceptação. \(y=−x+4\) Identifique a inclinação e a\(y\) interceptação. \(m=−1\) \(y\)-interceptar é\((0, 4)\) Faça um gráfico do\(y\) -intercept. Veja o gráfico abaixo. Identifique a ascensão e a corrida. \(m = \frac{-1}{1}\) Conte a subida e a corrida para marcar o segundo ponto. levante-se\(−1\), corra\(1\) Desenhe a linha. 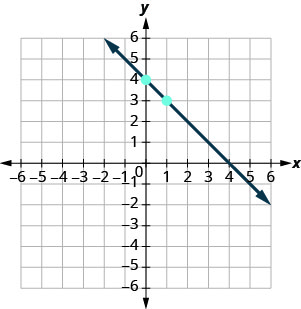
Para verificar seu trabalho, você pode encontrar outro ponto na linha e garantir que seja uma solução da equação. No gráfico, vemos a linha passar\((4, 0)\). - \(\begin{array}{l}{y=-x+4} \\ {0\stackrel{?}{=}-4+4} \\ {0=0\checkmark}\end{array}\)
Faça um gráfico da linha da equação\(y=−x−3\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
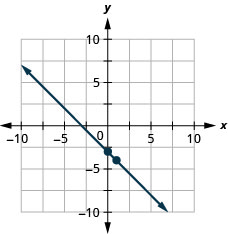
Faça um gráfico da linha da equação\(y=−x−1\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
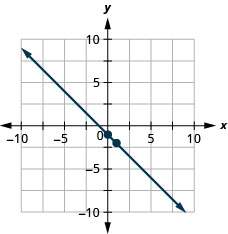
Faça um gráfico da linha da equação\(y=−\frac{2}{3}x−3\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
\(y=mx+b\) A equação está na forma de inclinação-interceptação. \(y=−\frac{2}{3}x−3\) Identifique a inclinação e a\(y\) interceptação. \(m = -\frac{2}{3}\);\(y\) -intercept é\((0, −3)\) Faça um gráfico do\(y\) -intercept. Veja o gráfico abaixo. Identifique a ascensão e a corrida. Conte a subida e a corrida para marcar o segundo ponto. Desenhe a linha. 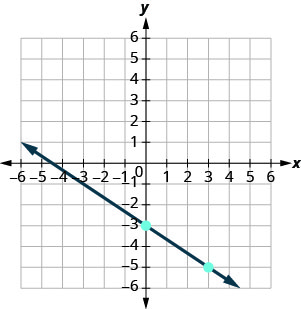
Faça um gráfico da linha da equação\(y=−\frac{5}{2}x+1\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
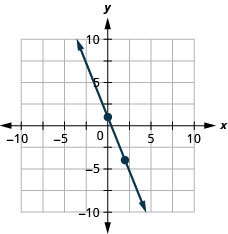
Faça um gráfico da linha da equação\(y=−\frac{3}{4}x−2\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
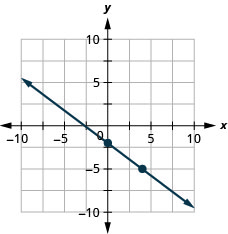
Faça um gráfico da linha da equação\(4x−3y=12\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
\(4x−3y=12\) Encontre a forma de inclinação e interceptação da equação. \(−3y=−4x+12\) \(−\frac{3y}{3}=\frac{−4x+12}{−3}\) A equação agora está na forma de inclinação-interceptação. \(y=\frac{4}{3}x−4\) Identifique a inclinação e a\(y\) interceptação. \(m=\frac{4}{3}\) \(y\)-Intercept é\((0, −4)\) Faça um gráfico do\(y\) -intercept. Veja o gráfico abaixo. Identifique a subida e a corrida; conte a subida e a corrida para marcar o segundo ponto. Desenhe a linha. 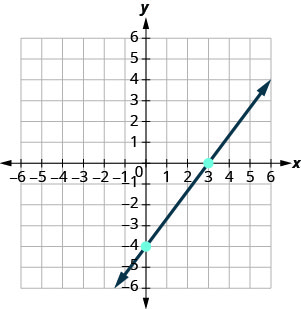
Faça um gráfico da linha da equação\(2x−y=6\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
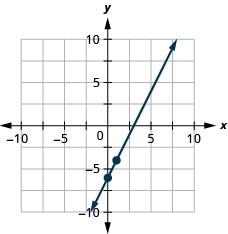
Faça um gráfico da linha da equação\(3x−2y=8\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
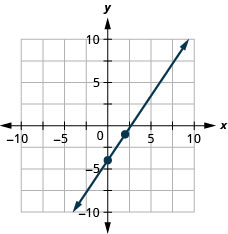
Usamos uma grade com\(x\) e\(y\) ambas indo de aproximadamente\(−10\) a para\(10\) para todas as equações que graficamos até agora. Nem todas as equações lineares podem ser representadas graficamente nessa pequena grade. Muitas vezes, especialmente em aplicativos com dados do mundo real, precisaremos estender os eixos para números positivos maiores ou menores negativos.
Faça um gráfico da linha da equação\(y=0.2x+45\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
Usaremos uma grade com os eixos indo\(−80\) de aproximadamente\(80\) a.
\(y=mx+b\) A equação está na forma de inclinação-interceptação. \(y=0.2x+45\) Identifique a inclinação e a\(y\) interceptação. \(m=0.2\) O\(y\) intercepto -é\((0, 45)\) Faça um gráfico do\(y\) -intercept. Veja o gráfico abaixo. Conte a subida e a corrida para marcar o segundo ponto. A inclinação é\(m=0.2\); na forma fracionária, isso significa\(m=\frac{2}{10}\). Dada a escala do nosso gráfico, seria mais fácil usar a fração equivalente\(m=\frac{10}{50}\). Desenhe a linha. 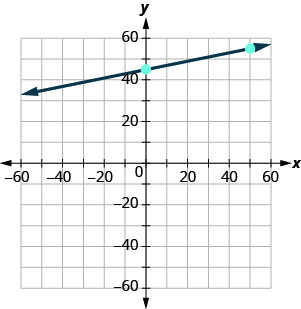
Faça um gráfico da linha da equação\(y=0.5x+25\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
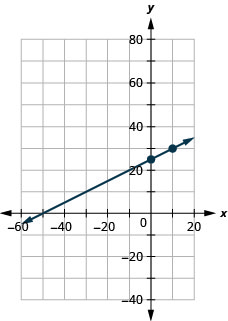
Faça um gráfico da linha da equação\(y=0.1x−30\) usando sua inclinação e\(y\) intercepto.
- Resposta
-
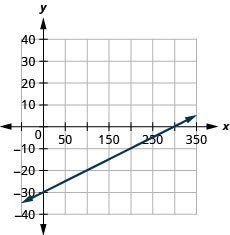
Agora que representamos graficamente as linhas usando a inclinação e o\(y\) -intercept, vamos resumir todos os métodos que usamos para representar graficamente as linhas. Veja a Figura\(\PageIndex{2}\).

Escolha o método mais conveniente para representar graficamente uma linha
Agora que vimos vários métodos que podemos usar para representar graficamente linhas, como sabemos qual método usar para uma determinada equação?
Embora possamos traçar pontos, usar a forma inclinação-interceptação ou encontrar os interceptos para qualquer equação, se reconhecermos a maneira mais conveniente de representar graficamente um determinado tipo de equação, nosso trabalho será mais fácil. Geralmente, traçar pontos não é a forma mais eficiente de representar graficamente uma linha. Vimos métodos melhores nas seções 4.3, 4.4 e anteriores nesta seção. Vamos procurar alguns padrões para ajudar a determinar o método mais conveniente para representar graficamente uma linha.
Aqui estão seis equações que representamos graficamente neste capítulo e o método que usamos para representar graficamente cada uma delas.
\[\begin{array}{lll}{\text{#1}}&{\text {Equation }} & {\text { Method }} \\ {\text{#2}}&{x=2} & {\text { Vertical line }} \\ {\text{#3}}&{y=4} & {\text { Hortical line }} \\ {\text{#4}}&{-x+2 y=6} & {\text { Intercepts }} \\ {\text{#5}}&{4 x-3 y=12} & {\text { Intercepts }} \\ {\text{#6}}&{y=4 x-2} & {\text { Slope-intercept }} \\{\text{#7}}& {y=-x+4} & {\text { Slope-intercept }}\end{array}\]
Cada uma das equações #1 e #2 tem apenas uma variável. Lembre-se de que, em equações dessa forma, o valor dessa variável é constante; não depende do valor da outra variável. Equações dessa forma têm gráficos que são linhas verticais ou horizontais.
Nas equações #3 e #4, ambas\(x\)\(y\) estão do mesmo lado da equação. Essas duas equações são da forma\(Ax+By=C\). Substituímos\(y=0\) para encontrar o\(x\) -intercept e\(x=0\) encontrar o\(y\) -intercept e, em seguida, encontramos um terceiro ponto escolhendo outro valor para\(x\) ou\(y\).
As equações #5 e #6 são escritas na forma inclinação-interceptação. Depois de identificar a inclinação e o\(y\) intercepto da equação, nós os usamos para representar graficamente a linha.
Isso leva à seguinte estratégia.
Considere a forma da equação.
- Se tiver apenas uma variável, é uma linha vertical ou horizontal.
- \(x=a\)é uma linha vertical que passa pelo\(x\) eixo -em\(a\).
- \(y=b\)é uma linha horizontal que passa pelo\(y\) eixo -em\(b\).
- Se\(y\) estiver isolado em um lado da equação, na forma\(y=mx+b\), faça um gráfico usando a inclinação e o\(y\) intercepto.
- Identifique a inclinação e a\(y\) interceptação e, em seguida, faça um gráfico.
- Se a equação for da forma\(Ax+By=C\), encontre as interceptações.
- Encontre as\(y\) interceptações\(x\) - e -, um terceiro ponto e, em seguida, faça um gráfico.
Determine o método mais conveniente para representar graficamente cada linha.
- \(y=−6\)
- \(5x−3y=15\)
- \(x=7\)
- \(y=\frac{2}{5}x−1\).
- Resposta
-
1. \(y=−6\)
Essa equação tem apenas uma variável,\(y\). Seu gráfico é uma linha horizontal cruzando o\(y\) eixo -em\(−6\).2. \(5x−3y=15\)
Essa equação é da forma\(Ax+By=C\). A maneira mais fácil de representar graficamente isso será encontrar as interceptações e mais um ponto.3. \(x=7\)
Há apenas uma variável,\(x\). O gráfico é uma linha vertical cruzando o\(x\) eixo -em\(7\).4. \(y=\frac{2}{5}x−1\)
Como essa equação está em\(y=mx+b\) forma, será mais fácil representar graficamente essa linha usando a inclinação e o\(y\) intercepto.
Determine o método mais conveniente para representar graficamente cada linha:
- \(3x+2y=12\)
- \(y=4\)
- \(y=\frac{1}{5}x−4\)
- \(x=−7\)
- Resposta
-
- intercepta
- linha horizontal
- inclinação—interceptação
- linha vertical
Determine o método mais conveniente para representar graficamente cada linha:
- \(x=6\)
- \(y=−\frac{3}{4}x+1\)
- \(y=−8\)
- \(4x−3y=−1\)
- Resposta
-
- linha vertical
- inclinação—interceptação
- linha horizontal
- intercepta
Represente graficamente e interprete aplicações de inclinação-interceptação
Muitas aplicações do mundo real são modeladas por equações lineares. Vamos dar uma olhada em algumas aplicações aqui para que você possa ver como as equações escritas em forma de inclinação e interceptação se relacionam com situações do mundo real.
Normalmente, quando uma equação linear modela uma situação do mundo real, letras diferentes são usadas para as variáveis, em vez de\(x\)\(y\) e. Os nomes das variáveis nos lembram de quais quantidades estão sendo medidas.
A equação\(F=\frac{9}{5}C+32\) é usada para converter temperaturas\(C\),, na escala Celsius em temperaturas,\(F\), na escala Fahrenheit.
- Encontre a temperatura em Fahrenheit para uma temperatura Celsius de\(0\).
- Encontre a temperatura em Fahrenheit para uma temperatura Celsius de\(20\).
- Interprete a inclinação e a\(F\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
1. \(\begin{array}{ll}{\text { Find the Fahrenheit temperature for a Celsius temperature of } 0 .} & {F=\frac{9}{5} C+32} \\ {\text { Find } F \text { when } C=0 .} & {F=\frac{9}{5}(0)+32} \\ {\text { Simplify. }} & {F=32}\end{array}\)
2. \ begin {array} {ll} {\ text {Encontre a temperatura em Fahrenheit para uma temperatura Celsius de} 20.} & {F=\ frac {9} {5} C+32}\\ {\ texto {Localizar} F\ texto {quando} C=20.} & {F=\ frac {9} {5} (20) +32}\\ {\ text {Simplifique.}} & {F=36+32}\\ {\ text {Simplifique.}} & {F=68}\ end {array}
3. Interprete a inclinação e a\(F\) interceptação da equação.
Embora essa equação use\(F\) e\(C\), ela ainda está na forma de inclinação-intercepto.
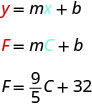
A inclinação,\(\frac{9}{5}\), significa que a temperatura Fahrenheit (\(F\)) aumenta em\(9\) graus quando a temperatura Celsius (\(C\)) aumenta em\(5\) graus.
O\(F\) intercepto -significa que quando a temperatura está\(0°\) na escala Celsius, ela está\(32°\) na escala Fahrenheit.
4. Faça um gráfico da equação.
Precisaremos usar uma escala maior do que a habitual. Comece no\(F\) intercepto -e\((0,32)\) depois conte a ascensão\(9\) e a corrida de\(5\) para obter um segundo ponto. Veja a Figura\(\PageIndex{3}\).
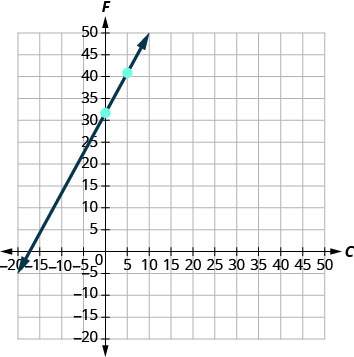
Figura\(\PageIndex{3}\)
A equação\(h=2s+50\) é usada para estimar a altura de uma mulher em polegadas,\(h\), com base no tamanho do sapato,\(s\).
- Estime a altura de uma criança que usa calçados femininos\(0\).
- Estime a altura de uma mulher com o tamanho do sapato\(8\).
- Interprete a inclinação e a\(h\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
- \(50\)polegadas
- \(66\)polegadas
- A inclinação,\(2\), significa que a altura,\(h\), aumenta em\(2\) centímetros quando o tamanho do sapato,\(s\), aumenta em\(1\). O\(h\) intercepto -significa que quando o tamanho do sapato é\(0\), a altura é em\(50\) polegadas.
A equação\(T=\frac{1}{4}n+40\) é usada para estimar a temperatura em graus Fahrenheit,\(T\), com base no número de chilros de críquete,\(n\), em um minuto.
- Faça uma estimativa da temperatura quando não houver chilros.
- Estime a temperatura quando for o número de chilros em um minuto\(100\).
- Interprete a inclinação e a\(T\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
- \(40\)graus
- \(65\)graus
- A inclinação,\(\frac{1}{4}\), significa que a temperatura Fahrenheit (\(F\)) aumenta\(1\) em grau quando o número de chilros,\(n\), aumenta em\(4\). O\(T\) intercepto -significa que quando o número de chilros é\(0\), a temperatura é\(40°\).
O custo de administrar alguns tipos de negócios tem dois componentes: um custo fixo e um custo variável. O custo fixo é sempre o mesmo, independentemente de quantas unidades são produzidas. Esse é o custo do aluguel, seguro, equipamento, publicidade e outros itens que devem ser pagos regularmente. O custo variável depende do número de unidades produzidas. É para o material e a mão de obra necessários para produzir cada item.
Stella tem um negócio doméstico que vende pizzas gourmet. A equação\(C=4p+25\) modela a relação entre seu custo semanal\(C\), em dólares,\(p\) e o número de pizzas que ela vende.
- Encontre o custo de Stella por uma semana quando ela não vende pizzas.
- Encontre o custo de uma semana quando ela vende\(15\) pizzas.
- Interprete a inclinação e a\(C\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
1. Encontre o custo de Stella por uma semana quando ela não vende pizzas. 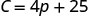
Descubra\(C\) quando\(p=0\). 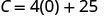
Simplifique. 
O custo fixo de Stella é\($25\) quando ela não vende pizzas. 2. Encontre o custo de uma semana quando ela vende\(15\) pizzas. 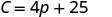
Descubra\(C\) quando\(p=15\). 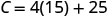
Simplifique. 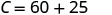

Os custos de Stella são\($85\) quando ela vende\(15\) pizzas. 3. Interprete a inclinação e a\(C\) interceptação da equação. 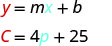
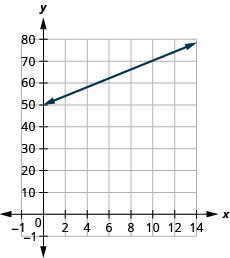
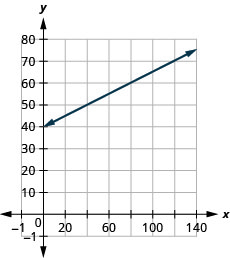
A inclinação,\(4\), significa que o custo aumenta em\($4\) cada pizza que Stella vende. O\(C\) -intercept significa que mesmo quando Stella não vende pizzas, seus custos da semana são\($25\). 4. Faça um gráfico da equação. Precisaremos usar uma escala maior do que a habitual. Comece no\(C\) intercepto -e\((0, 25)\) depois conte a ascensão\(4\) e a corrida de\(1\) para obter um segundo ponto. 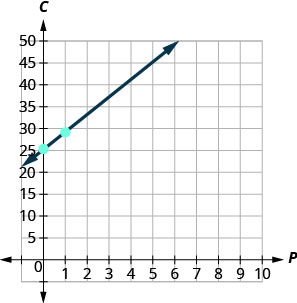
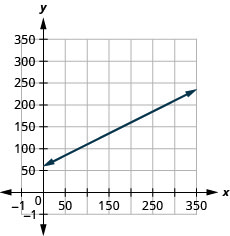
Sam dirige uma van de entrega. A equação\(C=0.5m+60\) modela a relação entre seu custo semanal\(C\), em dólares e o número de milhas,\(m\), que ele dirige.
- Encontre o custo de Sam por uma semana quando ele dirige\(0\) milhas.
- Encontre o custo de uma semana quando ele dirige\(250\) milhas.
- Interprete a inclinação e a\(C\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
- \($60\)
- \($185\)
- A inclinação,\(0.5\), significa que o custo semanal\(C\),, aumenta\($0.50\) quando o número de milhas percorridas,\(n\), aumenta em\(1\). O\(C\) -intercept significa que quando o número de milhas percorridas é\(0\), o custo semanal é\($60\).
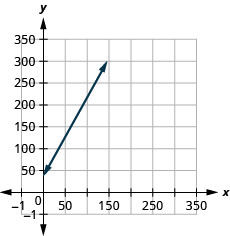
Loreen tem um negócio de caligrafia. A equação\(C=1.8n+35\) modela a relação entre seu custo semanal\(C\), em dólares e o número de convites de casamento,\(n\), que ela escreve.
- Encontre o custo de Loreen por uma semana quando ela não escreve convites.
- Encontre o custo de uma semana quando ela escreve\(75\) convites.
- Interprete a inclinação e a\(C\) interceptação da equação.
- Faça um gráfico da equação.
- Resposta
-
- \($35\)
- \($170\)
- A inclinação,\(1.8\), significa que o custo semanal\(C\),, aumenta\($1.80\) quando o número de convites,\(n\), aumenta em\(1.80\). O\(C\) -intercept significa que quando o número de convites é\(0\), o custo semanal é\($35\).
Use inclinações para identificar linhas paralelas
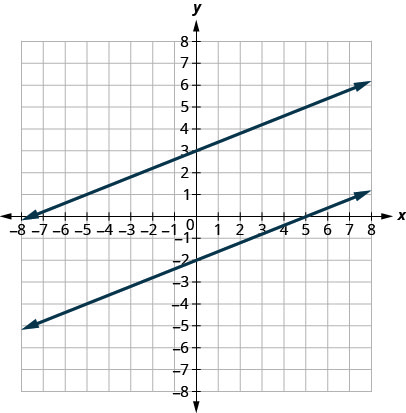
A inclinação de uma linha indica o quão íngreme é a linha e se ela sobe ou desce à medida que a lemos da esquerda para a direita. Duas retas que têm a mesma inclinação são chamadas de linhas paralelas. Linhas paralelas nunca se cruzam.

E quanto às linhas verticais? A inclinação de uma linha vertical é indefinida, então as linhas verticais não se encaixam na definição acima. Dizemos que as linhas verticais que têm diferentes\(x\) interceptações são paralelas. Veja a Figura\(\PageIndex{5}\).
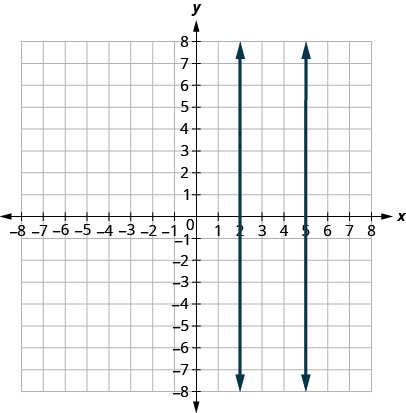
Linhas paralelas são linhas no mesmo plano que não se cruzam.
- As linhas paralelas têm a mesma inclinação e diferentes\(y\) interceptações.
- Se\(m_{1}\) e\(m_{2}\) são as inclinações de duas linhas paralelas, então\(m_{1} = m_{2}\).
- Linhas verticais paralelas têm diferentes\(x\) interceptações.
Vamos representar graficamente as equações\(y=−2x+3\) e\(2x+y=−1\) na mesma grade. A primeira equação já está na forma de inclinação-interceptação:\(y=−2x+3\). Resolvemos a segunda equação para\(y\):
\[\begin{aligned} 2x+y &=-1 \\ y &=-2x-1 \end{aligned}\]
Faça um gráfico das linhas.
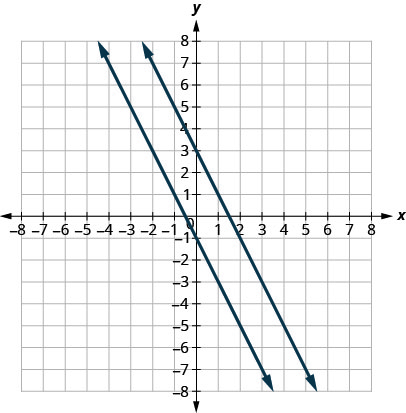
Observe que as linhas parecem paralelas. Qual é a inclinação de cada linha? Qual é a\(y\) interceptação de cada linha?
\[\begin{array}{lll} {y} & {=m x+b} & {y=m x+b} \\ {y} & {=-2 x+3} & {y=-2 x-1} \\ {m} & {=-2} & {m=-2}\\ {b} & {=3,(0,3)} & {b=-1,(0,-1)}\end{array}\]
As inclinações das linhas são as mesmas e a\(y\) interceptação de cada linha é diferente. Então, sabemos que essas linhas são paralelas.
Como as retas paralelas têm a mesma inclinação e diferentes\(y\) interceptações, agora podemos simplesmente observar a forma inclinada-interceptação das equações das retas e decidir se as retas são paralelas.
Use inclinações e\(y\) interceptações -para determinar se as linhas\(3x−2y=6\)\(y = \frac{3}{2}x + 1\) são paralelas.
- Resposta
-
\(\begin{array} {lrll} {\text { Solve the first equation for } y .} &{ 3 x-2 y} &{=} &{6}\\{} & {\frac{-2 y}{-2}} &{ =}&{-3 x+6 }\\ {} &{\frac{-2 y}{-2}}&{ =}&{\frac{-3 x+6}{-2}} \\ {} & {y }&{=}&{\frac{3}{2} x-3} \end{array}\)
A equação agora está na forma de inclinação-interceptação.
A equação da segunda linha já está na forma de inclinação-intercepto.
Identifique a inclinação e a\(y\) interceptação de ambas as linhas.
\(\begin{array}{lll}{y=\frac{3}{2} x+1} & {} & {y=\frac{3}{2} x-3} \\ {y=m x+b} & {} & {y=m x+b}\\ {m=\frac{3}{2}} & {} & {m=\frac{3}{2}} \\ {y\text{-intercept is }(0, 1)} & {} & {y\text{-intercept is }(0, −3)} \end{array}\)
As linhas têm a mesma inclinação e\(y\) interceptações diferentes e, portanto, são paralelas. Talvez você queira representar graficamente as linhas para confirmar se elas são paralelas.
Use inclinações e\(y\) interceptações -para determinar se as linhas\(2x+5y=5\)\(y=−\frac{2}{5}x−4\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(4x−3y=6\)\(y=\frac{4}{3}x−1\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=−4\)\(y=3\) são paralelas.
- Resposta
-
\(\begin{array}{llll}{\text{Write each equation in slope-intercept form.}} &{y=-4} & {\text { and }} &{ y=3} \\ {\text{Since there is no }x\text{ term we write }0x.} &{y=0 x-4} & {} &{y=0 x+3} \\ {\text{Identify the slope and }y\text{-intercept of both lines.}} &{y=m x+b} &{} & {y=m x+b} \\ {} &{m=0} &{} & {m=0} \\{} & {y\text {-intercept is }(0,4)} &{} & {y \text {-intercept is }(0,3)}\end{array}\)
As linhas têm a mesma inclinação e\(y\) interceptações diferentes e, portanto, são paralelas.
Há outra maneira de ver esse exemplo. Se você reconhecer imediatamente pelas equações que essas são linhas horizontais, sabe que suas inclinações são ambas\(0\). Como as linhas horizontais cruzam o\(y\) eixo -em\(y=−4\) e em\(y=3\), sabemos que as\(y\) interceptações -são\((0,−4)\)\((0,3)\) e. As linhas têm a mesma inclinação e\(y\) interceptações diferentes e, portanto, são paralelas.
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=8\)\(y=−6\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=1\)\(y=−5\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(x=−2\)\(x=−5\) são paralelas.
- Resposta
-
\[x=-2 \text { and } x=-5\]
Como não existe\(y\), as equações não podem ser colocadas na forma de inclinação e interceptação. Mas nós os reconhecemos como equações de linhas verticais. Suas\(x\) interceptações são\(−2\)\(−5\) e. Como suas\(x\) interceptações -são diferentes, as linhas verticais são paralelas.
Use inclinações e\(y\) interceptações -para determinar se as linhas\(x=1\)\(x=−5\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(x=8\)\(x=−6\) são paralelas.
- Resposta
-
paralelo
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=2x−3\)\(−6x+3y=−9\) são paralelas. Você também pode querer representar graficamente essas linhas para ver como elas se parecem.
- Resposta
-
\(\begin{array} {llll} {\text { The first equation is already in slope-intercept form. }} & {y=2x-3}&{}&{} \\ \\ {\text { Solve the second equation for } y} & {-6x+3y} &{=}&{-9} \\{} & {3y}&{=}&{6x-9} \\ {}&{\frac{3y}{3} }&{=}&{\frac{6x-9}{3}} \\{} & {y}&{=}&{2x-3}\end{array}\)
A segunda equação agora também está na forma de inclinação-intercepto.
Identifique a inclinação e a\(y\) interceptação de ambas as linhas.
\[\begin{array}{lll}{y=2x-3} &{} & {y=2x-3} \\ {y=mx+b} &{} & {y=mx+b} \\ {m=2} &{} & {m=2} \\ {\text{The }y\text{-intercept is }(0 ,−3)} &{} & {\text{The }y\text{-intercept is }(0 ,−3)} \end{array} \nonumber\]
As linhas têm a mesma inclinação, mas também têm as mesmas\(y\) interceptações. Suas equações representam a mesma linha. Eles não são paralelos; eles são a mesma linha.
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=−\frac{1}{2}x−1\)\(x+2y=2\) são paralelas.
- Resposta
-
não paralelo; mesma linha
Use inclinações e\(y\) interceptações -para determinar se as linhas\(y=\frac{3}{4}x−3\)\(3x−4y=12\) são paralelas.
- Resposta
-
não paralelo; mesma linha
Use inclinações para identificar linhas perpendiculares
Vejamos as linhas cujas equações são\(y=\frac{1}{4}x−1\) e\(y=−4x+2\), mostradas na Figura\(\PageIndex{5}\).
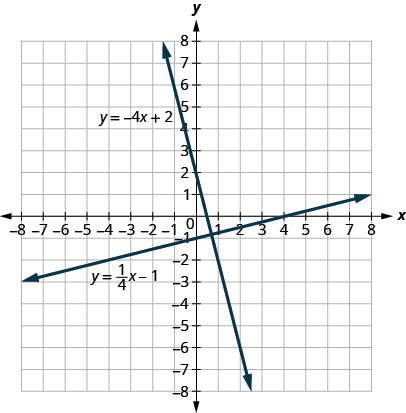
Essas linhas estão no mesmo plano e se cruzam em ângulos retos. Chamamos essas linhas de perpendiculares.
O que você nota sobre as inclinações dessas duas linhas? Conforme lemos da esquerda para a direita, a linha\(y=14x−1\) sobe, então sua inclinação é positiva. A linha\(y=−4x+2\) cai da esquerda para a direita, então tem uma inclinação negativa. Faz sentido para você que as inclinações de duas retas perpendiculares tenham sinais opostos?
Se observarmos a inclinação da primeira linha e a inclinação da segunda linha\(m_{2}=−4\), podemos ver que eles são recíprocos negativos um do outro.\(m_{1}=14\) Se os multiplicarmos, o produto deles é\(−1\).
\[\begin{array}{c}{m_{1} \cdot m_{2}} \\ {\frac{1}{4}(-4)} \\ {-1}\end{array}\]
Isso sempre é verdade para linhas perpendiculares e nos leva a essa definição.
As linhas perpendiculares são linhas no mesmo plano que formam um ângulo reto.
Se m1 e m2 são as inclinações de duas linhas perpendiculares, então:
\[m_{1} \cdot m_{2}=-1 \text { and } m_{1}=\frac{-1}{m_{2}}\]
As linhas verticais e horizontais são sempre perpendiculares entre si.
Conseguimos observar a forma inclinada-interceptação das equações lineares e determinar se as retas eram paralelas ou não. Podemos fazer a mesma coisa com linhas perpendiculares.
Encontramos a forma inclinação-interceptação da equação e, em seguida, vemos se as inclinações são recíprocas negativas. Se o produto das inclinações for\(−1\), as linhas são perpendiculares. As linhas perpendiculares podem ter as mesmas\(y\) interceptações.
Use inclinações para determinar se as linhas\(x−5y=5\) são perpendiculares.\(y=−5x−4\)
- Resposta
-
A primeira equação já está na forma de inclinação-interceptação:\(\quad y=−5x−4\)
\(\begin{array} {llll} {\text{Solve the second equation for }y.} &{x-5y} &{=} &{5} \\{} &{-5 y} &{=} &{-x+5} \\ {} & {\frac{-5 y}{-5}} &{=} &{\frac{-x+5}{-5}} \\ {} &{y} &{=} &{\frac{1}{5} x-1} \end{array}\)A segunda equação agora também está na forma de interceptação de inclinação.
\(\begin{array} {lrllllll} {\text{Identify the slope of each line.}} &{y} &{=} &{-5 x-4} & {} &{y} &{=} &{\frac{1}{5} x-1} \\ {} &{y} &{=} &{m x+b} & {} &{y} &{=} &{m x+b}\\ {} &{m_{1}} &{=}&{-5} & {} &{m_{2}} &{=}&{\frac{1}{5}}\end{array}\)
As inclinações são recíprocas negativas uma da outra, então as linhas são perpendiculares. Verificamos multiplicando as inclinações,
\[\begin{array}{l}{m_{1} \cdot m_{2}} \\ {-5\left(\frac{1}{5}\right)} \\ {-1\checkmark}\end{array}\]
Use inclinações para determinar se as linhas\(y=−3x+2\)\(x−3y=4\) são perpendiculares.
- Resposta
-
perpendiculares
Use inclinações para determinar se as linhas\(y=2x−5\)\(x+2y=−6\) são perpendiculares.
- Resposta
-
perpendiculares
Use inclinações para determinar se as linhas\(2x+7y=5\) são perpendiculares.\(7x+2y=3\)
- Resposta
-
\(\begin{array}{lrlrl}{\text{Solve the equations for y.}} &{7 x+2 y} & {=3} & {2 x+7 y}&{=}&{5} \\{} & {2 y} & {=-7 x+3} & {7 y}&{=}&{-2 x+5} \\ {} &{\frac{2 y}{2}} & {=\frac{-7 x+3}{2} \quad} & {\frac{7 y}{7}}&{=}&{\frac{-2 x+5}{7}} \\ {} &{y} & {=-\frac{7}{2} x+\frac{3}{2}} &{y}&{=}&{\frac{-2}{7}x + \frac{5}{7}}\\ \\{\text{Identify the slope of each line.}} & {y}&{=m x+b} &{y}&{=}&{m x+b} \\{} & {m_{1}} & {=-\frac{7}{2} }&{ m_{2}}&{=}&{-\frac{2}{7}}\end{array}\)
As inclinações são recíprocas umas das outras, mas têm o mesmo sinal. Como não são recíprocos negativos, as linhas não são perpendiculares.
Use inclinações para determinar se as linhas\(5x+4y=1\)\(4x+5y=3\) são perpendiculares.
- Resposta
-
não perpendicular
Use inclinações para determinar se as linhas\(2x−9y=3\)\(9x−2y=1\) são perpendiculares.
- Resposta
-
não perpendicular
Acesse este recurso on-line para obter instruções e práticas adicionais com gráficos.
Conceitos-chave
- A forma inclinação-interceptação de uma equação de uma reta com inclinação mm e\(y\) -intercepto,\((0,b)\) é,\(y=mx+b\).
- Representar graficamente uma linha usando sua inclinação e\(y\) -Intercept
- Encontre a forma de interceptação de inclinação da equação da reta.
- Identifique a inclinação e a\(y\) interceptação.
- Faça um gráfico do\(y\) -intercept.
- Use a fórmula da inclinação\(m = \dfrac{\text{rise}}{\text{run}}\) para identificar a subida e a corrida.
- Começando na\(y\) interceptação -, conte a subida e corra para marcar o segundo ponto.
- Conecte os pontos com uma linha.
- Estratégia para escolher o método mais conveniente para representar graficamente uma linha: considere a forma da equação.
- Se tiver apenas uma variável, é uma linha vertical ou horizontal.
\(x = a\)é uma linha vertical que passa pelo\(x\) eixo -em a.
\(y = b\) é uma linha horizontal que passa pelo\(y\) eixo -em\(b\). - Se\(y\) estiver isolado em um lado da equação, na forma\(y=mx+b\), faça um gráfico usando a inclinação e o\(y\) intercepto.
Identifique a inclinação e a\(y\) interceptação e, em seguida, faça um gráfico. - Se a equação for da forma\(Ax+By=C\), encontre as interceptações.
Encontre as\(y\) interceptações\(x\) - e -, um terceiro ponto e, em seguida, faça um gráfico.
- Se tiver apenas uma variável, é uma linha vertical ou horizontal.
- Linhas paralelas são linhas no mesmo plano que não se cruzam.
- As linhas paralelas têm a mesma inclinação e diferentes\(y\) interceptações.
- Se\(m_1\) e\(m_2\) são as inclinações de duas linhas paralelas, então\(m_1 = m_2\).
- Linhas verticais paralelas têm diferentes\(x\) interceptações.
- As linhas perpendiculares são linhas no mesmo plano que formam um ângulo reto.
- Se\(m_1\) e\(m_2\) são as inclinações de duas linhas perpendiculares, então\(m_1\cdot m_2=−1\)\(m_1=\frac{−1}{m_2}\) e.
- As linhas verticais e horizontais são sempre perpendiculares entre si.
Glossário
- linhas paralelas
- Linhas no mesmo plano que não se cruzam.
- linhas perpendiculares
- Linhas no mesmo plano que formam um ângulo reto.
- forma de interceptação de inclinação de uma equação de uma reta
- A forma inclinação-interceptação de uma equação de uma reta com inclinação mm e\(y\) -intercepto,\((0,b)\) é,\(y=mx+b\).


