4.4: Entendendo a inclinação de uma linha
- Page ID
- 184216
- Ao final desta seção, você poderá:
- Use geoboards para modelar a inclinação
- Use\(m = \frac{\text{rise}}{\text{run}}\) para encontrar a inclinação de uma linha a partir de seu gráfico
- Encontre a inclinação das linhas horizontais e verticais
- Use a fórmula da inclinação para encontrar a inclinação de uma linha entre dois pontos
- Faça um gráfico de uma linha com um ponto e a inclinação
- Resolva aplicações de inclinação
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\frac{1 - 4}{8 - 2}\).
Se você perdeu esse problema, revise o Exercício 1.6.31 - Divida:\(\frac{0}{4}, \frac{4}{0}\).
Se você perdeu esse problema, revise o Exercício 1.10.16. - Simplifique:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
Se você perdeu esse problema, revise o Exercício 1.6.4.
Ao representar graficamente equações lineares, você pode notar que algumas linhas se inclinam para cima à medida que vão da esquerda para a direita e algumas linhas se inclinam para baixo. Algumas linhas são muito íngremes e outras mais planas. O que determina se uma linha se inclina para cima ou para baixo ou se é íngreme ou plana?
Em matemática, a “inclinação” de uma linha é chamada de inclinação da linha. O conceito de inclinação tem muitas aplicações no mundo real. A inclinação de um telhado, o nível de uma rodovia e uma rampa para uma cadeira de rodas são alguns exemplos em que você literalmente vê encostas. E quando você anda de bicicleta, sente a inclinação ao subir ou descer a costa.
Nesta seção, exploraremos o conceito de inclinação.
Use placas geográficas para modelar a inclinação
Um geoboard é uma placa com uma grade de pinos nela. Usar elásticos em um geoboard nos dá uma maneira concreta de modelar linhas em uma grade de coordenadas. Ao esticar um elástico entre dois pinos em um geoboard, podemos descobrir como encontrar a inclinação de uma linha.
Fazer a atividade de Matemática Manipulativa “Explorando a inclinação” ajudará você a desenvolver uma melhor compreensão da inclinação de uma linha. (O papel quadriculado pode ser usado em vez de um geoboard, se necessário.)Começaremos esticando um elástico entre dois pinos, conforme mostrado na Figura\(\PageIndex{1}\).
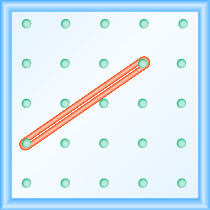
Não parece uma linha?
Agora, esticamos uma parte do elástico diretamente do pino esquerdo e ao redor de um terceiro pino para formar os lados de um triângulo reto, conforme mostrado na Figura\(\PageIndex{2}\)
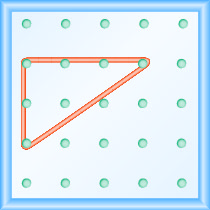
Criamos cuidadosamente um ângulo de 90º ao redor do terceiro pino, para que uma das linhas recém-formadas seja vertical e a outra horizontal.
Para encontrar a inclinação da linha, medimos a distância ao longo dos lados vertical e horizontal do triângulo. A distância vertical é chamada de subida e a distância horizontal é chamada de corrida, conforme mostrado na Figura\(\PageIndex{3}\).
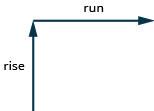
Se nosso geoboard e elástico se parecerem exatamente com os mostrados na Figura\(\PageIndex{4}\), o aumento é 2. O elástico sobe 2 unidades. (Cada espaço é uma unidade.)
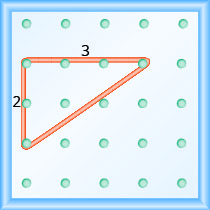
O aumento neste geoboard é 2, à medida que o elástico sobe duas unidades.
O que é a corrida?
O elástico tem 3 unidades. A corrida é 3 (veja a Figura\(\PageIndex{4}\)).
A inclinação de uma linha é a razão entre a subida e a corrida. Em matemática, é sempre referido com a letra m.
A inclinação de uma linha de uma linha é\(m = \frac{\text{rise}}{\text{run}}\).
A subida mede a mudança vertical e a corrida mede a mudança horizontal entre dois pontos na linha.
Qual é a inclinação da linha no geoboard na Figura\(\PageIndex{4}\)?
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]
A linha tem inclinação\(\frac{2}{3}\). Isso significa que a linha aumenta 2 unidades para cada 3 unidades de corrida.
Quando trabalhamos com geoboards, é uma boa ideia adquirir o hábito de começar em um pino à esquerda e conectá-lo a um pino à direita. Se o aumento subir, é positivo e, se cair, é negativo. A corrida vai da esquerda para a direita e será positiva.
Qual é a inclinação da linha no geoboard mostrado?
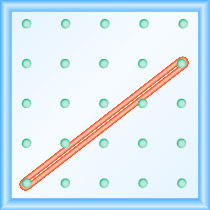
- Responda
-
Use a definição de inclinação:\(m = \frac{\text{rise}}{\text{run}}\).
Comece pelo pino esquerdo e conte os espaços para cima e para a direita para alcançar o segundo pino.
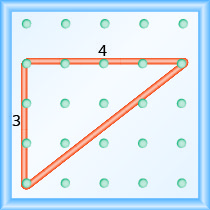
\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]
Isso significa que a linha aumenta 3 unidades para cada 4 unidades de corrida.
Qual é a inclinação da linha no geoboard mostrado?
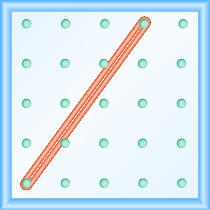
- Responda
-
\(\frac{4}{3}\)
Qual é a inclinação da linha no geoboard mostrado?
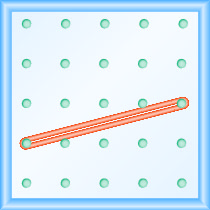
- Responda
-
\(\frac{1}{4}\)
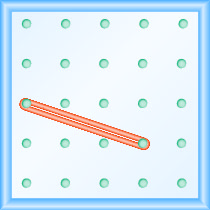
Qual é a inclinação da linha no geoboard mostrado?
- Responda
-
Use a definição de inclinação:\(m = \frac{\text{rise}}{\text{run}}\).
Comece no pino esquerdo e conte as unidades para baixo e para a direita para alcançar o segundo pino.
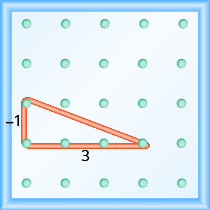
\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]
Isso significa que a linha descarta 1 unidade para cada 3 unidades de corrida.
Qual é a inclinação da linha no geoboard?
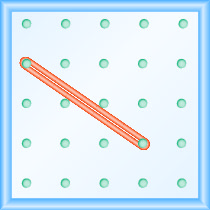
- Responda
-
\(-\frac{2}{3}\)
Qual é a inclinação da linha no geoboard?
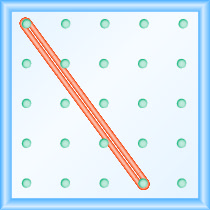
- Responda
-
\(-\frac{4}{3}\)
Observe que no Exercício\(\PageIndex{1}\) a inclinação é positiva e no Exercício\(\PageIndex{4}\) a inclinação é negativa. Você percebe alguma diferença nas duas linhas mostradas na Figura (a) e na Figura (b)?
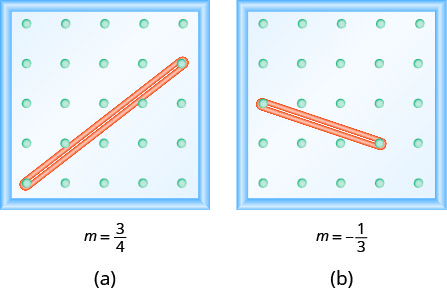
Nós “lemos” uma linha da esquerda para a direita, assim como lemos palavras em inglês. Conforme você lê da esquerda para a direita, a linha na Figura (a) está subindo; ela tem inclinação positiva. A linha na Figura (b) está descendo; tem inclinação negativa.

Use um geoboard para modelar uma linha com inclinação\(\frac{1}{2}\).
- Responda
-
Para modelar uma linha em um geoboard, precisamos da subida e da corrida.
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)
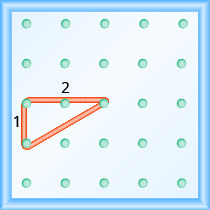
A hipotenusa do triângulo reto formado pelo elástico representa uma linha cuja inclinação é\(\frac{1}{2}\).
Modele a inclinação\(m = \frac{1}{3}\). Faça um desenho para mostrar seus resultados.
- Responda
-
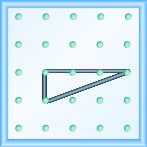
Modele a inclinação\(m = \frac{3}{2}\). Faça um desenho para mostrar seus resultados.
- Responda
-

Use um geoboard para modelar uma linha com inclinação\(\frac{-1}{4}\).
- Responda
-
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)
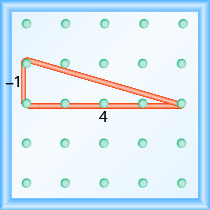
A hipotenusa do triângulo reto formado pelo elástico representa uma linha cuja inclinação é\(\frac{-1}{4}\).
Modele a inclinação\(m = \frac{-2}{3}\). Faça um desenho para mostrar seus resultados.
- Responda
-
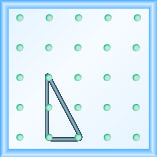
Modele a inclinação\(m = \frac{-1}{3}\). Faça um desenho para mostrar seus resultados.
- Responda
-
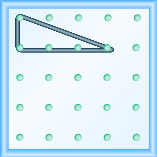
Use\(m = \frac{\text{rise}}{\text{run}}\) para encontrar a inclinação de uma reta a partir de seu gráfico
Agora, veremos alguns gráficos no plano de coordenadas xy e veremos como encontrar suas inclinações. O método será muito semelhante ao que acabamos de modelar em nossas placas geográficas.
Para encontrar a inclinação, devemos contar a subida e a corrida. Mas por onde começamos?
Localizamos dois pontos na linha cujas coordenadas são números inteiros. Em seguida, começamos com o ponto à esquerda e esboçamos um triângulo reto, para que possamos contar a subida e a corrida.
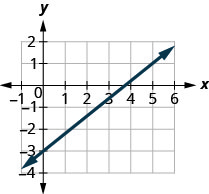
Encontre a inclinação da linha mostrada.
- Responda
-



Encontre a inclinação da linha mostrada.
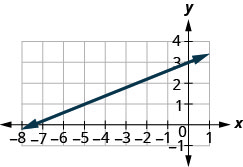
- Responda
-
\(\frac{2}{5}\)
Encontre a inclinação da linha mostrada.
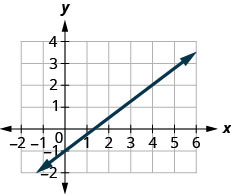
- Responda
-
\(\frac{3}{4}\)
- Localize dois pontos na linha cujas coordenadas são números inteiros.
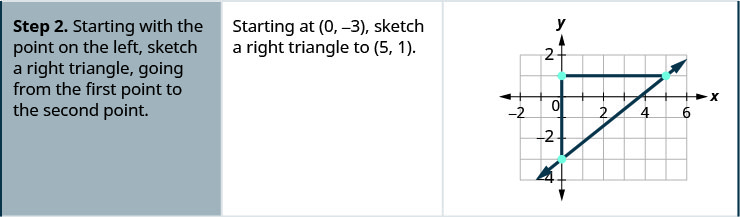
- Começando com o ponto à esquerda, desenhe um triângulo reto, indo do primeiro ponto ao segundo ponto.
- Conte a subida e a corrida nas pernas do triângulo.
- Pegue a proporção de subida para correr para encontrar a inclinação,\(m = \frac{\text{rise}}{\text{run}}\).
Encontre a inclinação da linha mostrada.
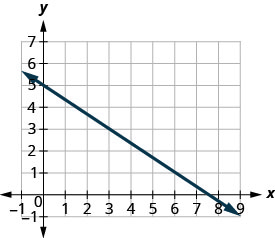
- Responda
-
Localize dois pontos no gráfico cujas coordenadas são números inteiros. (0,5) e (3,3) Qual ponto está à esquerda? (0,5) Começando em (0,5), desenhe um triângulo reto até (3,3). 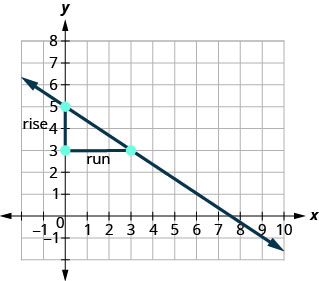
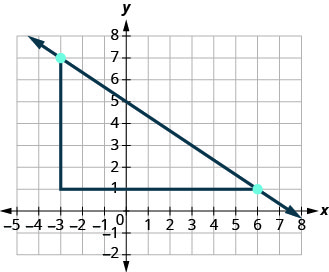
Conte o aumento — é negativo. O aumento é de −2. Conte a corrida. A corrida é 3. Use a fórmula da inclinação. \(m = \frac{\text{rise}}{\text{run}}\) Substitua os valores da subida e da corrida. \(m = \frac{-2}{3}\) Simplifique. \(m = -\frac{2}{3}\) A inclinação da linha é\(-\frac{2}{3}\). Então y aumenta em 3 unidades à medida que xx diminui em 2 unidades.
E se usássemos os pontos (−3,7) e (6,1) para encontrar a inclinação da reta?
-
O aumento seria −6 e a corrida seria 9. Então\(m = \frac{-6}{9}\), e isso simplifica para\(m = -\frac{2}{3}\). Lembre-se de que não importa quais pontos você usa — a inclinação da linha é sempre a mesma.
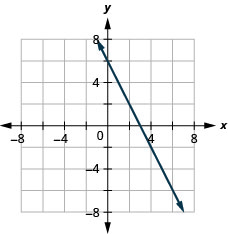
Encontre a inclinação da linha mostrada.
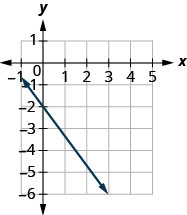
- Responda
-
\(-\frac{4}{3}\)
Encontre a inclinação da linha mostrada.
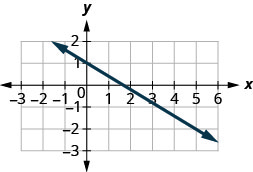
- Responda
-
\(-\frac{3}{5}\)
Nos dois últimos exemplos, as linhas tinham interceptações y com valores inteiros, então era conveniente usar o intercepto y como um dos pontos para encontrar a inclinação. No próximo exemplo, o intercepto y é uma fração. Em vez de usar esse ponto, procuraremos outros dois pontos cujas coordenadas são números inteiros. Isso facilitará os cálculos da inclinação.
Encontre a inclinação da linha mostrada.

- Responda
-
Localize dois pontos no gráfico cujas coordenadas são números inteiros. (2,3) e (7,6) Qual ponto está à esquerda? (2,3) Começando em (2,3), desenhe um triângulo reto até (7,6). 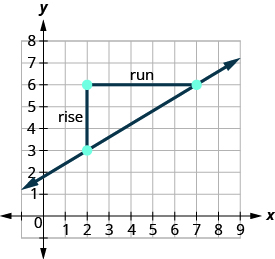
Conte o aumento. O aumento é 3. Conte a corrida. A corrida é 5. Use a fórmula da inclinação. \(m = \frac{\text{rise}}{\text{run}}\) Substitua os valores da subida e da corrida. \(m = \frac{3}{5}\) A inclinação da linha é\(\frac{3}{5}\). Isso significa que y aumenta 5 unidades à medida que x aumenta 3 unidades.
Quando usamos geoboards para introduzir o conceito de inclinação, dissemos que sempre começávamos com o ponto à esquerda e contávamos a subida e a corrida para chegar ao ponto à direita. Dessa forma, a corrida sempre foi positiva e a subida determinou se a inclinação era positiva ou negativa.
O que aconteceria se começássemos com o ponto à direita?
Vamos usar os pontos (2,3) e (7,6) novamente, mas agora vamos começar em (7,6).
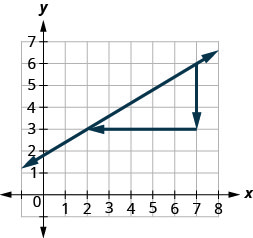
- \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
- Não importa por onde você começa, a inclinação da linha é sempre a mesma.
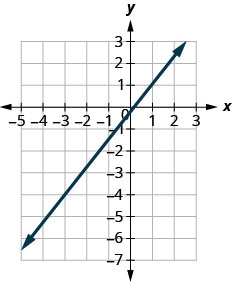
Encontre a inclinação da linha mostrada.
- Responda
-
\(\frac{5}{4}\)
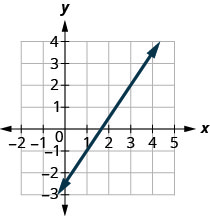
Encontre a inclinação da linha mostrada.
- Responda
-
\(\frac{3}{2}\)
Encontre a inclinação das linhas horizontais e verticais
Você se lembra do que havia de especial nas linhas horizontais e verticais? Suas equações tinham apenas uma variável.
\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]
Então, como podemos encontrar a inclinação da linha horizontal y=4y=4? Uma abordagem seria representar graficamente a linha horizontal, encontrar dois pontos nela e contar a subida e a corrida. Vamos ver o que acontece quando fazemos isso.
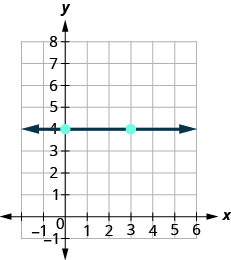
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)
Todas as linhas horizontais têm inclinação 0. Quando as coordenadas y são iguais, o aumento é 0.
A inclinação de uma linha horizontal, y=b, é 0.
O piso do seu quarto é horizontal. Sua inclinação é 0. Se você colocasse cuidadosamente uma bola no chão, ela não rolaria.
Agora, vamos considerar uma linha vertical, a linha.
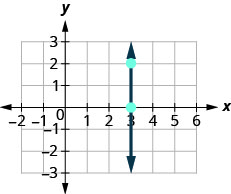
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)
Mas não podemos dividir por 0. A divisão por 0 não está definida. Então, dizemos que a inclinação da linha vertical x=3x=3 é indefinida.
A inclinação de qualquer linha vertical é indefinida. Quando as coordenadas x de uma linha são todas iguais, a execução é 0.
A inclinação de uma linha vertical, x=a, é indefinida.
Encontre a inclinação de cada linha:
ⓐ x=8 ⓑ y=−5.
- Responda
-
ⓐ x=8
Essa é uma linha vertical.
Sua inclinação é indefinida.
ⓑ y=−5
Essa é uma linha horizontal.
Tem inclinação 0.
Encontre a inclinação da reta: x=−4.
- Responda
-
indefinida
Encontre a inclinação da linha: y=7.
- Responda
-
0
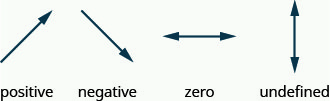
Lembre-se de que “lemos” uma linha da esquerda para a direita, assim como lemos palavras escritas em inglês.
Use a fórmula de inclinação para encontrar a inclinação de uma linha entre dois pontos
Fazer a atividade de matemática manipulativa “Inclinação das linhas entre dois pontos” ajudará você a desenvolver uma melhor compreensão de como encontrar a inclinação de uma reta entre dois pontos.Às vezes, precisaremos encontrar a inclinação de uma linha entre dois pontos quando não temos um gráfico para contar a subida e a corrida. Poderíamos traçar os pontos em papel de grade e, em seguida, contar a subida e a corrida, mas, como veremos, existe uma maneira de encontrar a inclinação sem representar graficamente. Antes de chegarmos a isso, precisamos introduzir alguma notação algébrica.
Vimos que um par ordenado (x, y) fornece as coordenadas de um ponto. Mas quando trabalhamos com inclinações, usamos dois pontos. Como o mesmo símbolo (x, y) pode ser usado para representar dois pontos diferentes? Os matemáticos usam subscritos para distinguir os pontos.
\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]
O uso de assinaturas em matemática é muito parecido com o uso das iniciais do sobrenome no ensino fundamental. Talvez você se lembre de Laura C. e Laura M. em sua turma da terceira série?
Usaremos\(\left(x_{1}, y_{1}\right)\) para identificar o primeiro ponto e\(\left(x_{2}, y_{2}\right)\) identificar o segundo ponto.
Se tivéssemos mais de dois pontos, poderíamos usar\(\left(x_{3}, y_{3}\right)\)\(\left(x_{4}, y_{4}\right)\), e assim por diante.
Vamos ver como a subida e a corrida se relacionam com as coordenadas dos dois pontos, dando outra olhada na inclinação da linha entre os pontos (2,3) e (7,6).
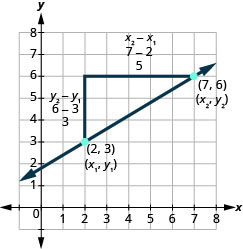
Como temos dois pontos, usaremos a notação subscrita,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\).
No gráfico, contamos o aumento de 3 e a corrida de 5.
Observe que o aumento de 3 pode ser encontrado subtraindo as coordenadas y 6 e 3.
\[3=6-3\]
E a sequência de 5 pode ser encontrada subtraindo as coordenadas x 7 e 2.
\[5 = 7 - 2\]
Nós sabemos\(m = \frac{\text{rise}}{\text{run}}\). Então\(m = \frac{3}{5}\).
Reescrevemos a ascensão e a corrida colocando as coordenadas\(m = \frac{6-3}{7-2}\)
Mas 6 é y2, a coordenada y do segundo ponto e 3 é y1, a coordenada y do primeiro ponto.
Assim, podemos reescrever a inclinação usando a notação subscrita. \(m = \frac{y2-y1}{7-2}\)
Além disso, 7 é x2, a coordenada x do segundo ponto e 2 é x1, a coordenada x do primeiro ponto.
Então, novamente, reescrevemos a inclinação usando a notação subscrita. \(m = \frac{y2-y1}{x2-x1}\)
Mostramos que\(m = \frac{y2-y1}{x2-x1}\) é realmente outra versão do\(m = \frac{\text{rise}}{\text{run}}\). Podemos usar essa fórmula para encontrar a inclinação de uma reta quando temos dois pontos na linha.
A inclinação da linha entre dois pontos\(\left(x_{1}, y_{1}\right)\) e\(\left(x_{2}, y_{2}\right)\) é
\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
Essa é a fórmula da inclinação.
A inclinação é:
\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]
Use a fórmula da inclinação para encontrar a inclinação da linha entre os pontos (1,2) e (4,5).
- Responda
-
\(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)
Vamos confirmar isso contando a inclinação em um gráfico usando\(m = \frac{\text{rise}}{\text{run}}\).
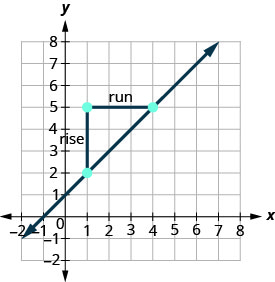
Não importa qual ponto você chama de ponto #1 e qual você chama de ponto #2. A inclinação será a mesma. Experimente você mesmo o cálculo.
Use a fórmula da inclinação para encontrar a inclinação da linha através dos pontos: (8,5) e (6,3).
- Responda
-
1
Use a fórmula da inclinação para encontrar a inclinação da linha através dos pontos: (1,5) e (5,9).
- Responda
-
1
Use a fórmula da inclinação para encontrar a inclinação da reta através dos pontos (−2, −3) e (−7,4).
- Responda
-
\(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)
Vamos verificar essa inclinação no gráfico mostrado.
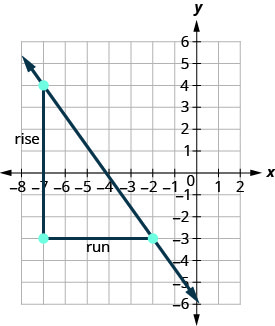
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]
Use a fórmula da inclinação para encontrar a inclinação da reta através dos pontos: (−3,4) e (2, −1).
- Responda
-
-1
Use a fórmula da inclinação para encontrar a inclinação da reta através do par de pontos: (−2,6) e (−3, −4).
- Responda
-
10
Representar graficamente uma linha com um ponto e a inclinação
Até agora, neste capítulo, representamos graficamente linhas traçando pontos, usando interceptações e reconhecendo linhas horizontais e verticais.
Um outro método que podemos usar para representar graficamente linhas é chamado de método ponto-inclinação. Usaremos esse método quando conhecermos um ponto e a inclinação da linha. Começaremos traçando o ponto e depois usaremos a definição de inclinação para desenhar o gráfico da linha.
Faça um gráfico da linha que passa pelo ponto (1, −1) cuja inclinação é\(m = \frac{3}{4}\).
- Responda
-




Faça um gráfico da linha que passa pelo ponto (2, −2) com a inclinação\(m = \frac{4}{3}\).
- Responda
-
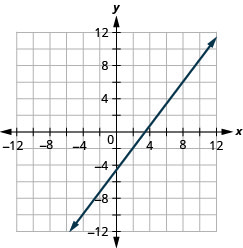
Faça um gráfico da linha que passa pelo ponto (−2,3) com a inclinação\(m=\frac{1}{4}\).
- Responda
-
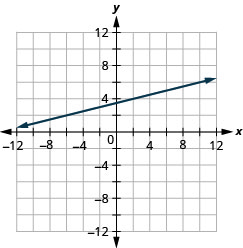
- Faça um gráfico do ponto dado.
- Use a fórmula da inclinação\(m=\frac{\text { rise }}{\text { rise }}\) para identificar a subida e a corrida.
- Começando no ponto determinado, conte a subida e corra para marcar o segundo ponto.
- Conecte os pontos com uma linha.
Faça um gráfico da linha com y -intercept 2 cuja inclinação é\(m=−\frac{2}{3}\).
- Responda
-
Faça um gráfico do ponto dado, o intercepto y, (0,2).
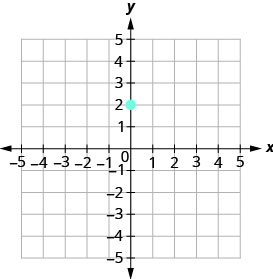
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)
Conte a ascensão e a corrida. Marque o segundo ponto.
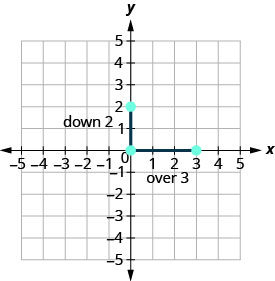
-
Conecte os dois pontos com uma linha.
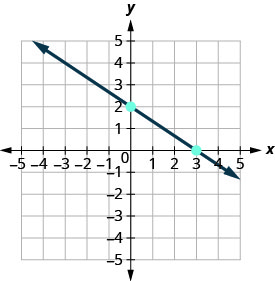
-
Você pode verificar seu trabalho encontrando um terceiro ponto. Como a inclinação é\(m=−\frac{2}{3}\), ela pode ser escrita como\(m=\frac{2}{-3}\). Volte para (0,2) e conte a subida, 2, e a corrida, −3.
Faça um gráfico da linha com o intercepto y 4 e a inclinação\(m=−\frac{5}{2}\).
- Responda
-
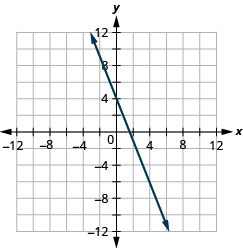
Faça um gráfico da linha com o intercepto x −3 e a inclinação\(m=−\frac{3}{4}\).
- Responda
-
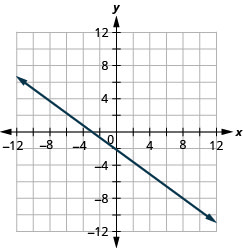
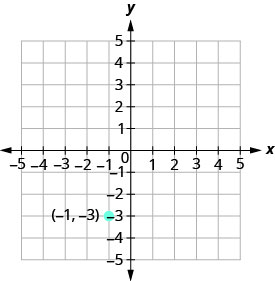
Faça um gráfico da linha que passa pelo ponto (−1, −3) cuja inclinação é m=4.
- Responda
-
Faça um gráfico do ponto dado.
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)
Conte a subida e corra e marque o segundo ponto.
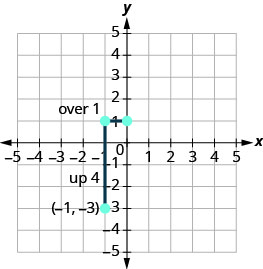
-
Conecte os dois pontos com uma linha.
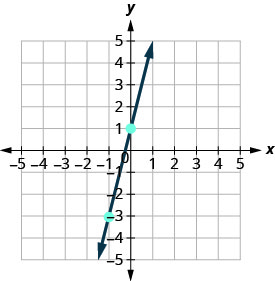
-
Você pode verificar seu trabalho encontrando um terceiro ponto. Como a inclinação é m = 4, ela pode ser escrita como\(m = \frac{-4}{-1}\). Volte para (−1, −3) e conte a subida, −4, e a corrida, −1.
Faça um gráfico da linha com o ponto (−2,1) e a inclinação m=3.
- Responda
-
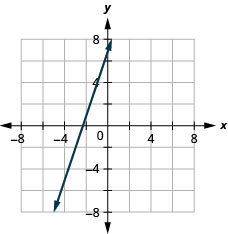
Faça um gráfico da linha com o ponto (4, −2) e a inclinação m=−2.
- Responda
-
Resolva aplicações de inclinação
No início desta seção, dissemos que existem muitas aplicações de inclinação no mundo real. Vamos dar uma olhada em alguns agora.
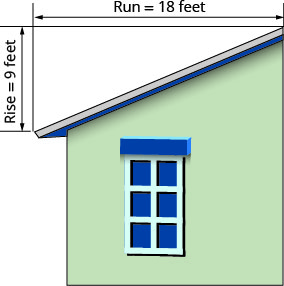
A “inclinação” do telhado de um edifício é a inclinação do telhado. Saber o campo é importante em climas onde há fortes nevascas. Se o telhado for muito plano, o peso da neve pode causar o colapso. Qual é a inclinação do telhado mostrada?
- Responda
-
\(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)
Use Exercício\(\PageIndex{40}\), substituindo o aumento = 14 e corrida = 24.
- Responda
-
\(\frac{7}{12}\)
Use Exercício\(\PageIndex{40}\), substituindo aumento = 15 e corrida = 36.
- Responda
-
\(\frac{5}{12}\)
Você já pensou nos canos de esgoto que vão da sua casa para a rua? Eles devem se inclinar uma\(\frac{1}{4}\) polegada por pé para drenar adequadamente. Qual é a inclinação necessária?

- Responda
-
\(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)
O tubo cai 1 polegada para cada 48 polegadas de percurso horizontal.
Encontre a inclinação de um cano que desce uma\(\frac{1}{3}\) polegada por pé.
- Responda
-
\(-\frac{1}{36}\)
Encontre a inclinação de um cano que desce uma\(\frac{3}{4}\) polegada por metro.
- Responda
-
\(-\frac{1}{48}\)
Acesse esses recursos on-line para obter instruções e práticas adicionais para entender a inclinação de uma linha.
Conceitos-chave
- Encontre a inclinação de uma linha a partir de seu gráfico usando\(m=\frac{\text { rise }}{\text { run }}\)
- Localize dois pontos na linha cujas coordenadas são números inteiros.
- Começando com o ponto à esquerda, desenhe um triângulo reto, indo do primeiro ponto ao segundo ponto.
- Conte a subida e a corrida nas pernas do triângulo.
- Pegue a proporção de subida para correr para encontrar a inclinação.
- Representar graficamente uma linha com um ponto e a inclinação
- Faça um gráfico do ponto dado.
- Use a fórmula da inclinação\(m=\frac{\text { rise }}{\text { run }}\) para identificar a subida e a corrida.
- Começando no ponto determinado, conte a subida e corra para marcar o segundo ponto.
- Conecte os pontos com uma linha.
- Inclinação de uma linha horizontal
- A inclinação de uma linha horizontal, y=b, é 0.
- Inclinação de uma linha vertical
- A inclinação de uma linha vertical, x=a, é indefinida


