3.3: Resolver aplicações de mistura

Last updated
Save as PDF

Page ID: 184338

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Resolva problemas de palavras-moeda
Resolva problemas com tickets e palavras de carimbo
Resolva problemas de mistura de palavras
Use o modelo de mistura para resolver problemas de investimento usando juros simples

Nota

Antes de começar, faça este teste de prontidão.

Multiplique:$14(0.25)$.
Se você perdeu esse problema, revise o Exercício 1.8.19.
Resolver:$0.25x+0.10(x+4)=2.5$.
Se você perdeu esse problema, revise o Exercício 2.4.22.
O número de moedas de dez centavos é três a mais do que o número de trimestres. Deixe q representar o número de trimestres. Escreva uma expressão para o número de moedas de dez centavos.
Se você perdeu esse problema, revise o Exercício 1.3.43.

Resolva problemas de palavras-moeda

Em problemas de mistura, teremos dois ou mais itens com valores diferentes para combinar. O modelo de mistura é usado por mercearias e bartenders para garantir que eles estabeleçam preços justos para os produtos que vendem. Muitos outros profissionais, como químicos, banqueiros de investimento e paisagistas, também usam o modelo de mistura.

Nota

Fazendo a atividade de matemática manipulativa, o Coin Lab ajudará você a desenvolver uma melhor compreensão dos problemas de mistura de palavras.

Começaremos analisando um aplicativo com o qual todos estão familiarizados: dinheiro!

Imagine que pegamos um punhado de moedas de um bolso ou bolsa e as colocamos em uma mesa. Como determinaríamos o valor dessa pilha de moedas? Se pudermos formar um plano passo a passo para encontrar o valor total das moedas, isso nos ajudará a começar a resolver problemas de palavras com moedas.

Então, o que faríamos? Para ordenar a bagunça das moedas, poderíamos separar as moedas em pilhas de acordo com seu valor. Os quartos seriam com quartos, moedas de dez centavos com moedas de dez centavos, níquel com níquel e assim por diante. Para obter o valor total de todas as moedas, adicionaríamos o valor total de cada pilha.

Pilhas de moedas de um centavo, níquel, moedas de dez centavos e moedas — Figura$\PageIndex{1}$

Como determinaríamos o valor de cada pilha? Pense na pilha de moedas de dez centavos: quanto ela vale? Se contarmos o número de moedas de dez centavos, saberemos quantas temos — o número de moedas de dez centavos.

Mas isso não nos diz o valor de todas as moedas de dez centavos. Digamos que contamos 17 centavos, quanto eles valem? Cada centavo vale $0,10 — esse é o valor de um centavo. Para encontrar o valor total da pilha de 17 centavos, multiplique 17 por $0,10 para obter $1,70. Esse é o valor total de todas as 17 moedas de dez centavos. Esse método leva ao seguinte modelo.

VALOR TOTAL DAS MOEDAS

Para o mesmo tipo de moeda, o valor total de várias moedas é encontrado usando o modelo

\[number\cdot value = total\space value\]

onde
número é o número de moedas

valor é o valor de cada moeda

valor total é o valor total de todas as moedas

O número de moedas de dez centavos vezes o valor de cada centavo é igual ao valor total das moedas de dez centavos.

\[\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}\]

Poderíamos continuar esse processo para cada tipo de moeda e então saberíamos o valor total de cada tipo de moeda. Para obter o valor total de todas as moedas, adicione o valor total de cada tipo de moeda.

Vamos analisar um caso específico. Suponha que haja 14 quartos, 17 centavos, 21 centavos e 39 centavos.

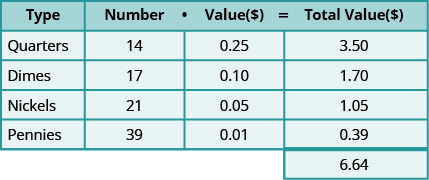
$Essa tabela tem cinco linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Trimestres, 14, 0,25 e 3,50. A terceira linha diz Dimes, 17, 0,10 e 1,70. A quarta linha diz Níquéis, 21, 0,05 e 1,05. A quinta linha diz Pennies, 39, 0,01 e 0,39. A célula extra diz 6,64.$

Tabela$\PageIndex{1}$

O valor total de todas as moedas é de $6,64.

Observe como o gráfico ajuda a organizar todas as informações! Vamos ver como usamos esse método para resolver um problema de palavra-moeda.

Exemplo$\PageIndex{1}$

Adalberto tem $2,25 em moedas de dez centavos e moedas no bolso. Ele tem nove moedas a mais do que moedas de dez centavos. Quantos de cada tipo de moeda ele tem?

Solução

Etapa 1. Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.

Determine os tipos de moedas envolvidas.
Pense na estratégia que usamos para encontrar o valor de um punhado de moedas. A primeira coisa que precisamos é observar quais tipos de moedas estão envolvidas. Adalberto tem moedas e moedas de dez centavos. Crie uma tabela para organizar as informações. Veja o gráfico abaixo.

Rotule as colunas como “tipo”, “número”, “valor” e “valor total”.
Liste os tipos de moedas.
Escreva o valor de cada tipo de moeda.
Escreva o valor total de todas as moedas.

Podemos resolver esse problema tudo em centavos ou em dólares. Aqui faremos isso em dólares e colocaremos o cifrão ($) na tabela como um lembrete.
O valor de um centavo é $0,10 e o valor de um níquel é $0,05. O valor total de todas as moedas é de $2,25. A tabela abaixo mostra essas informações.
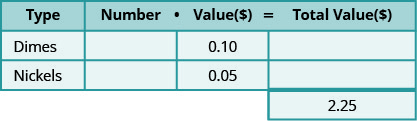
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Dimes, blank, 0.10 e blank. A terceira linha diz Níquéis, em branco, 0,05 e em branco. A célula extra diz 2,25.$

Etapa 2. Identifique o que estamos procurando.

Somos solicitados a encontrar o número de moedas de dez centavos e níqueis que Adalberto tem.

Etapa 3. Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.

Use expressões variáveis para representar o número de cada tipo de moeda e escrevê-las na tabela.

Multiplique o número vezes o valor para obter o valor total de cada tipo de moeda.

Em seguida, contamos o número de cada tipo de moeda. Neste problema, não podemos contar cada tipo de moeda — é isso que você está procurando — mas temos uma pista. Há nove centavos a mais do que moedas de dez centavos. O número de níquel é nove a mais do que o número de moedas de dez centavos.

\[\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}\]

Preencha a coluna “número” na tabela para ajudar a organizar tudo.

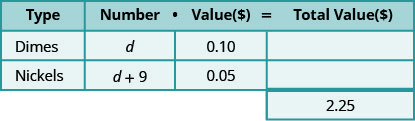
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Dimes, d, 0,10 e em branco. A terceira linha diz Níquéis, d mais 9, 0,05 e em branco. A célula extra diz 2,25.$

Agora temos todas as informações de que precisamos sobre o problema!

Multiplicamos o número vezes o valor para obter o valor total de cada tipo de moeda. Embora não saibamos o número real, temos uma expressão para representá-lo.

E agora multiplique$\text{number}\cdot\text{value}=\text{total value}$. Veja como isso é feito na tabela abaixo.

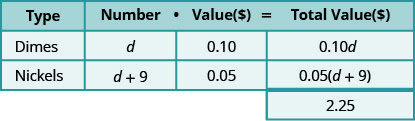
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Dimes, d, 0,10 e 0,10d. A terceira linha diz Níquéis, d mais 9, 0,05 e 0,05 vezes a quantidade (d mais 9). A célula extra diz 2,25.$

Observe que fizemos com que o cabeçalho da tabela mostrasse o modelo.

Etapa 4. Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase. Traduza a frase em inglês em uma equação algébrica.

Escreva a equação adicionando os valores totais de todos os tipos de moedas.

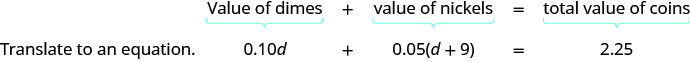
$A frase, “valor de moedas de dez centavos mais valor de níquel é igual ao valor total das moedas”, pode ser traduzida para uma equação. Traduza “valor de moedas” para 0,10d, traduza “valor de níquel” para 0,05d e traduza “valor total das moedas” para 2,25. A equação completa é 0,10d mais 0,05 vezes a quantidade d mais 9 é igual a 2,25.$

Etapa 5. Resolva a equação usando boas técnicas de álgebra.

Agora resolva essa equação.	$.$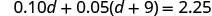
Distribuir.	$.$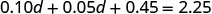
Combine termos semelhantes.	$.$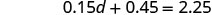
Subtraia 0,45 de cada lado.	$.$
Divida.	$.$
Então, há 12 moedas de dez centavos.
O número de níquel é d+9d+9.	$.$
	$.$
	21

Etapa 6. Verifique a resposta do problema e verifique se faz sentido.

Isso verifica?

\[\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}\]

Etapa 7. Responda à pergunta com uma frase completa.

Adalberto tem doze centavos e vinte e um centavos.

Se fosse um exercício de lição de casa, nosso trabalho poderia ter a seguinte aparência.

$Um trabalho de casa escrito em papel forrado de folhas soltas. A tarefa diz: “Adalberto tem 2 dólares e 25 centavos em moedas de dez centavos e moedas no bolso. Ele tem nove moedas a mais do que moedas de dez centavos. Quantos de cada tipo ele tem?” Abaixo está uma tabela. A primeira linha da tabela é uma linha de cabeçalho e cada célula nomeia a coluna ou colunas abaixo dela. A primeira célula da esquerda é chamada de “Tipo”. A segunda célula contém a equação “Número” vezes “Valor” é igual a “Valor total”, com uma coluna correspondendo a “Número”, uma coluna correspondendo a “Valor” e uma coluna correspondendo ao valor total. Portanto, o conteúdo da coluna “Número” vezes o conteúdo da coluna “Valor” é igual ao conteúdo da coluna “Valor total”. Na segunda linha da tabela, a coluna “Tipo” contém “Dimes”, a coluna “Número” contém d, a coluna “Valor” contém 0,10 e a coluna “Valor total” contém 0,10d. Na terceira linha da tabela, a coluna “Tipo” contém “Níquéis”, a coluna “Número” contém d mais 9, a coluna “Valor” contém 0,05 e a coluna “Valor total” contém 0,05 vezes a quantidade d mais 9. Uma linha abaixo, a coluna “Valor total” contém mais uma célula, que contém 2,25. Abaixo da tabela está a equação 0,10d mais 0,05d mais 0,45 é igual a 2,25. Abaixo disso está 0,15d mais 0,45 é igual a 2,25. Abaixo disso, 0,15d é igual a 1,80. À direita está d mais 9, o que se traduz em 12 mais 9 ou 21 níquel. À direita está o estágio de verificação, onde vemos se 12 moedas de dez centavos e 21 centavos equivalem a 2 dólares e 25 centavos. 12 vezes 0,10 é igual a 1,20 e 21 vezes (0,05) é igual a 1,05. 1,20 mais 1,05 é igual a 2,25.$

Experimente$\PageIndex{1}$

Michaela tem $2,05 em moedas de dez centavos e moedas em sua bolsa de moedas. Ela tem sete moedas a mais do que moedas. Quantas moedas de cada tipo ela tem?

Resposta: 9 níqueis, 16 moedas de dez centavos

Experimente$\PageIndex{2}$

Liliana tem $2,10 em moedas e moedas na mochila. Ela tem 12 centavos a mais do que moedas. Quantas moedas de cada tipo ela tem?

Resposta: 17 níqueis, 5 quartos

RESOLVA PROBLEMAS DE PALAVRAS-MOEDAS

Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Determine os tipos de moedas envolvidas.
- Crie uma tabela para organizar as informações.
- Rotule as colunas como “tipo”, “número”, “valor” e “valor total”.
- Liste os tipos de moedas.
- Escreva o valor de cada tipo de moeda.
- Escreva o valor total de todas as moedas.
Identifique o que estamos procurando.
Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Use expressões variáveis para representar o número de cada tipo de moeda e escrevê-las na tabela.
- Multiplique o número vezes o valor para obter o valor total de cada tipo de moeda.
Traduza em uma equação.
Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em uma equação.
Escreva a equação adicionando os valores totais de todos os tipos de moedas.
Resolva a equação usando boas técnicas de álgebra.
Verifique a resposta do problema e verifique se faz sentido.
Responda à pergunta com uma frase completa.

Exemplo$\PageIndex{2}$

Maria tem $2,43 em moedas e centavos em sua carteira. Ela tem o dobro de centavos do que moedas. Quantas moedas de cada tipo ela tem?

Solução

Etapa 1. Leia o problema.

Determine os tipos de moedas envolvidas.

Sabemos que Maria tem moedas e moedas de um centavo.

Crie uma tabela para organizar as informações.

Etapa 2. Identifique o que você está procurando.
- Estamos procurando o número de moedas e moedas de um centavo.
Etapa 3. Nome. Represente o número de trimestres e centavos usando variáveis.
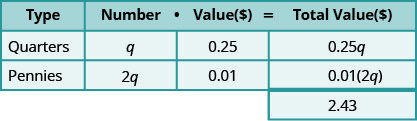
- Multiplique o 'número' e o 'valor' para obter o 'valor total' de cada tipo de moeda. $Sem texto alternativo$
  Etapa 4. Traduzir. Escreva a equação adicionando o “valor total” de todos os tipos de moedas.
  
  $\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}$
  $\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}$
  $\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}$

Experimente$\PageIndex{3}$

Sumanta tem $4,20 em moedas e moedas de dez centavos em seu cofrinho. Ela tem o dobro de centavos do que moedas de dez centavos. Quantas moedas de cada tipo ela tem?

Resposta: 42 níqueis, 21 moedas de dez centavos

Experimente$\PageIndex{4}$

Alison tem três vezes mais moedas de dez centavos do que moedas na bolsa. Ela tem $9,35 no total. Quantas moedas de cada tipo ela tem?

Resposta: 51 centavos, 17 quartos

No próximo exemplo, mostraremos somente a tabela completa — lembre-se das etapas que tomamos para preencher a tabela.

Exemplo$\PageIndex{3}$

Danny tem $2,14 em centavos e moedas em seu cofrinho. O número de centavos é dois a mais de dez vezes o número de centavos. Quantos centavos e quantos centavos Danny tem?

Solução

Etapa 1. Leia o problema.
Determine os tipos de moedas envolvidas.	centavos e moedas
Crie uma tabela.
Escreva o valor de cada tipo de moeda.	Os centavos valem $0,01. Os níquéis valem $0,05.
Etapa 2. Identifique o que estamos procurando.	o número de centavos e centavos
Etapa 3. Nome. Represente o número de cada tipo de moeda usando variáveis.
O número de centavos é definido em termos do número de centavos, então comece com centavos.	Deixe$p=$ o número de centavos.
O número de centavos é dois a mais de dez vezes o número de centavos.	E deixe$10p+2=$ o número de moedas.
Multiplique o número e o valor para obter o valor total de cada tipo de moeda.
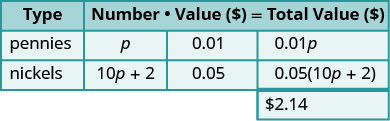$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz centavos, p, 0,01 e 0,01p. A terceira linha lê níquel, 10p mais 2, 0,05 e 0,05 vezes a quantidade (10p mais 2). A célula extra diz $2,14.$
Etapa 4. Traduzir. Escreva a equação adicionando o valor total de todos os tipos de moedas.	$.$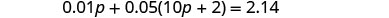
Etapa 5. Resolva a equação.	$.$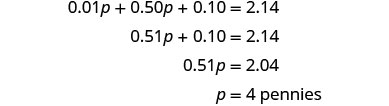
Quantos centavos?	$.$
Etapa 6. Verifique a resposta do problema e certifique-se de que faz sentido Danny ter quatro centavos e 42 centavos. O valor total é de $2,14? $\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	Danny tem quatro centavos e 42 centavos.

Experimente$\PageIndex{5}$

Jesse tem $6,55 em moedas e moedas no bolso. O número de níquel é cinco a mais do que duas vezes o número de trimestres. Quantos centavos e quantos quartos Jesse tem?

Resposta: 41 níquel, 18 quartos

Experimente$\PageIndex{6}$

Elane tem um total de $7,00 em moedas de dez centavos e moedas em seu frasco de moedas. O número de moedas de dez centavos que Elane tem é sete menos do que três vezes o número de níqueis. Quantas de cada moeda Elane tem?

Resposta: 22 níqueis, 59 moedas de dez centavos

Resolva problemas com tickets e palavras de carimbo

Problemas envolvendo bilhetes ou selos são muito parecidos com problemas com moedas. Cada tipo de bilhete e selo tem um valor, assim como cada tipo de moeda. Portanto, para resolver esses problemas, seguiremos as mesmas etapas que usamos para resolver problemas com moedas.

Exemplo$\PageIndex{4}$

Em um concerto escolar, o valor total dos ingressos vendidos foi de $1.506. Ingressos para estudantes vendidos por $6 cada e ingressos para adultos vendidos por $9 cada. O número de ingressos para adultos vendidos foi cinco a menos do que três vezes o número de ingressos para estudantes vendidos. Quantos ingressos para estudantes e quantos ingressos para adultos foram vendidos?

Solução

Etapa 1. Leia o problema.

Determine os tipos de tíquetes envolvidos. Existem ingressos para estudantes e ingressos para adultos.
Crie uma tabela para organizar as informações.

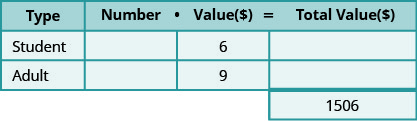
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Student, em branco, 6 e em branco. A terceira linha diz Adulto, em branco, 9 e em branco. A célula extra diz 1506.$

Etapa 2. Identifique o que estamos procurando.

Estamos procurando o número de ingressos para estudantes e adultos.

Etapa 3. Nome. Represente o número de cada tipo de ticket usando variáveis.

Sabemos que o número de ingressos para adultos vendidos foi cinco a menos do que três vezes o número de ingressos para estudantes vendidos.

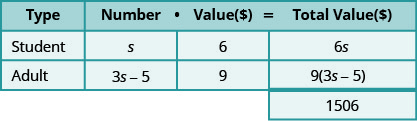
Multiplique o número pelo valor para obter o valor total de cada tipo de ingresso. $Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Student, s, 6 e 6s. A terceira linha diz Adulto, 3s menos 5, 9 e 9 vezes a quantidade (3s menos 5). A célula extra diz 1506.$
Etapa 4. Traduzir. Escreva a equação adicionando os valores totais de cada tipo de ticket.

\[6 s+9(3 s-5)=1506 \nonumber\]

Etapa 5. Resolva a equação.

\[\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber\]

Etapa 6. Verifique a resposta.

Havia 47 ingressos estudantis a $6 cada e 136 ingressos para adultos a $9 cada. O valor total é de $1.506? Encontramos o valor total de cada tipo de ingresso multiplicando o número de ingressos por seu valor e adicionamos para obter o valor total de todos os ingressos vendidos.

\[\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber\]

Etapa 7. Responda à pergunta. Eles venderam 47 ingressos para estudantes e 136 ingressos para adultos.

Experimente$\PageIndex{7}$

No primeiro dia de um torneio de pólo aquático, o valor total dos ingressos vendidos foi de $17.610. Os passes de um dia são vendidos por $20 e os passes para torneios são vendidos por $30. O número de passes para torneios vendidos foi 37 a mais do que o número de passes diários vendidos. Quantos passes diários e quantos passes para torneios foram vendidos?

Resposta: 330 passes de dias, 367 passes para torneios

Experimente$\PageIndex{8}$

No cinema, o valor total dos ingressos vendidos foi de $2.612,50. Ingressos para adultos vendidos por $10 cada e ingressos para idosos/crianças vendidos por $7,50 cada. O número de ingressos para idosos/crianças vendidos foi 25 menos do que o dobro do número de ingressos para adultos vendidos. Quantos ingressos para idosos/crianças e quantos ingressos para adultos foram vendidos?

Resposta: 112 ingressos para adultos, 199 ingressos para idosos/crianças

Aprendemos como encontrar o número total de ingressos quando o número de um tipo de ingresso é baseado no número do outro tipo. A seguir, veremos um exemplo em que sabemos o número total de ingressos e precisamos descobrir como os dois tipos de ingressos se relacionam.

Suponha que Bianca tenha vendido um total de 100 ingressos. Cada ingresso era um ingresso para adulto ou infantil. Se ela vendeu 20 ingressos para crianças, quantos ingressos para adultos ela vendeu?

Você disse '80'? Como você descobriu isso? Você subtraiu 20 de 100?

Se ela vendeu 45 ingressos infantis, quantos ingressos para adultos ela vendeu?

Você disse '55'? Como você o encontrou? Subtraindo 45 de 100?

E se ela vendesse 75 ingressos infantis? Quantos ingressos para adultos ela vendeu?

O número de ingressos para adultos deve ser de 100 a 75. Ela vendeu 25 ingressos para adultos.

Agora, suponha que Bianca vendeu x ingressos infantis. Então, quantos ingressos para adultos ela vendeu? Para descobrir, seguiríamos a mesma lógica que usamos acima. Em cada caso, subtraímos o número de ingressos infantis de 100 para obter o número de ingressos para adultos. Agora fazemos o mesmo com x.

Resumimos isso abaixo.

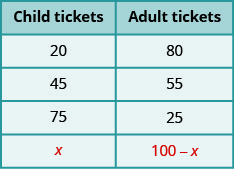
$Essa tabela tem cinco linhas e duas colunas. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita ingressos infantis e ingressos para adultos. A segunda linha diz 20 e 80. A terceira linha diz 45 e 55. A quarta linha diz 75 e 25. A quinta linha diz x e 100 mais x.$

Tabela$\PageIndex{2}$

Podemos aplicar essas técnicas a outros exemplos

Exemplo$\PageIndex{5}$

Galeno vendeu 810 ingressos para o carnaval de sua igreja por um total de $2.820. Os ingressos para crianças custam $3 cada e os ingressos para adultos custam $5 cada. Quantos ingressos para crianças e quantos ingressos para adultos ele vendeu?

Solução

Etapa 1. Leia o problema.

Determine os tipos de tíquetes envolvidos. Existem ingressos para crianças e ingressos para adultos.
Crie uma tabela para organizar as informações.

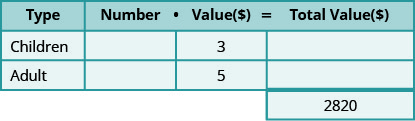
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Filhos, em branco, 3 e em branco. A terceira linha diz Adulto, em branco, 5 e em branco. A célula extra diz 2820.$

Etapa 2. Identifique o que estamos procurando.

Estamos procurando o número de ingressos para crianças e adultos.

Etapa 3. Nome. Represente o número de cada tipo de ticket usando variáveis.

Sabemos que o número total de ingressos vendidos foi 810.
Isso significa que o número de ingressos para crianças mais o número de ingressos para adultos deve somar 810.
$c$Seja o número de ingressos para crianças.

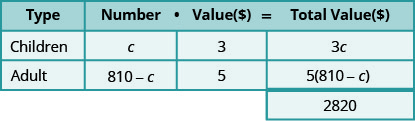
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha diz Crianças, c, 3 e 3c. A terceira linha diz Adulto, 810 menos c, 5 e 5 vezes a quantidade (810 menos c). A célula extra diz 2820.$

Então$810−c$ é o número de ingressos para adultos.
Multiplique o número pelo valor para obter o valor total de cada tipo de ingresso.

Etapa 4. Traduzir.

Escreva a equação adicionando os valores totais de cada tipo de ticket.

Etapa 5. Resolva a equação.

\[\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}\]

Quantos adultos?

\[\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber\]

Etapa 6. Verifique a resposta. Havia 615 ingressos para crianças a $3 cada e 195 ingressos para adultos a $5 cada. O valor total é de $2.820?

\[\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber\]

Etapa 7. Responda à pergunta. Galen vendeu 615 ingressos para crianças e 195 ingressos para adultos.

Experimente$\PageIndex{9}$

Durante seu turno na bilheteria do museu, Leah vendeu 115 ingressos, totalizando $1.163. Os ingressos para adultos custam $12 e os ingressos para estudantes custam $5. Quantos ingressos para adultos e quantos ingressos para estudantes Leah vendeu?

Resposta: 84 ingressos para adultos, 31 ingressos para estudantes

Experimente$\PageIndex{10}$

Um navio de observação de baleias tinha 40 passageiros pagantes a bordo. O total arrecadado com os ingressos foi de $1.196. Passageiros com tarifa integral pagaram $32 cada e passageiros com tarifa reduzida pagaram $26 cada. Quantos passageiros com tarifa integral e quantos passageiros com tarifa reduzida estavam no navio?

Resposta: 26% de tarifa integral, 14% de tarifa reduzida

Agora, faremos uma em que preenchemos a tabela de uma só vez.

Exemplo$\PageIndex{6}$

Monica pagou $8,36 por selos. O número de selos de 41 centavos era quatro a mais do que o dobro do número de selos de dois centavos. Quantos selos de 41 centavos e quantos selos de dois centavos a Monica comprou?

Solução

Os tipos de selos são selos de 41 centavos e selos de dois centavos. Seus nomes também dão valor!

“O número de selos de 41 centavos era quatro a mais do que o dobro do número de selos de dois centavos.”

\[\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber\]

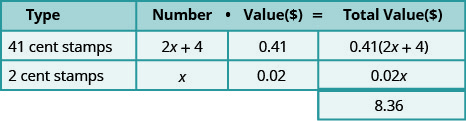
$Essa tabela tem três linhas e quatro colunas com uma célula extra na parte inferior da quarta coluna. A linha superior é uma linha de cabeçalho que lê da esquerda para a direita Tipo, Número, Valor ($) e Valor Total ($). A segunda linha lê selos de 41 centavos, 2x mais 4, 0,41 e 0,41 vezes a quantidade (2x mais 4). A terceira linha diz selos de 2 centavos, x, 0,02 e 0,02x. A célula extra diz 8,36.$

\[\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber\]

Verifique.

\[\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}\]
\[\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber\]

Experimente$\PageIndex{11}$

Eric pagou $13,36 por selos. O número de selos de 41 centavos era oito a mais do que o dobro do número de selos de dois centavos. Quantos selos de 41 centavos e quantos selos de dois centavos Eric comprou?

Resposta: 32 a $0,41, 12 a $0,02

Experimente$\PageIndex{12}$

Kailee pagou $12,66 por selos. O número de selos de 41 centavos era quatro a menos de três vezes o número de selos de 20 centavos. Quantos selos de 41 centavos e quantos selos de 20 centavos Kailee comprou?

Resposta: 26 a $0,41, 10 a $0,20

Resolva problemas de mistura de palavras

Agora vamos resolver algumas aplicações mais gerais do modelo de mistura. Mercearias e bartenders usam o modelo de mistura para definir um preço justo para um produto feito com a mistura de dois ou mais ingredientes. Os planejadores financeiros usam o modelo misto quando investem dinheiro em uma variedade de contas e desejam encontrar a taxa de juros geral. Os paisagistas usam o modelo de mistura quando têm uma variedade de plantas e um orçamento fixo, e os coordenadores de eventos fazem o mesmo ao escolher aperitivos e entradas para um banquete.

Nosso primeiro problema de mistura de palavras será fazer uma mistura de trilhas com passas e nozes.

Exemplo$\PageIndex{7}$

Henning está misturando passas e nozes para fazer 10 quilos de mistura de trilhas. As passas custam $2 a libra e as nozes custam $6 a libra. Se Henning quiser que seu custo para a mistura de trilhas seja de $5,20 a libra, quantos quilos de passas e quantos quilos de nozes ele deve usar?

Solução

Como antes, preenchemos um gráfico para organizar nossas informações.

Os 10 quilos de mistura de trilhas virão da mistura de passas e nozes.

\[\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber\]

Nós inserimos o preço por libra para cada item.

Multiplicamos o número vezes o valor para obter o valor total.

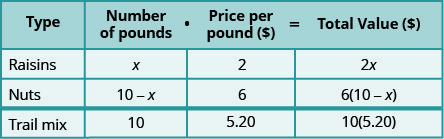
$Essa tabela tem quatro linhas e quatro colunas. A linha superior é uma linha de cabeçalho que diz da esquerda para a direita Tipo, Número de libras, Preço por libra ($) e Valor Total ($). A segunda linha diz passas, x, 2 e 2x. A terceira linha diz nozes, 10 menos x, 6 e 6 vezes a quantidade (10 menos x). A quarta linha diz mix de trilhas, 10, 5,20 e 10 vezes 5,20.$

Observe que a última linha na tabela fornece as informações para a quantidade total da mistura.

Sabemos que o valor das passas mais o valor das nozes será o valor da mistura da trilha.

Escreva a equação a partir dos valores totais.	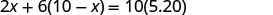$Exemplo: 3.32.jpg$
Resolva a equação.	$.$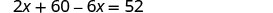
	$.$
	$.$
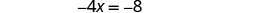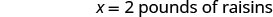Encontre o número de quilos de nozes.	$.$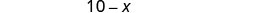
	$.$
	8 libras de nozes
Verifique. $\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}$
	Henning misturou dois quilos de passas com oito quilos de nozes.

Experimente$\PageIndex{13}$

Orlando está misturando quadrados de nozes e cereais para fazer uma mistura de festa. As nozes são vendidas por $7 a libra e os quadrados de cereais são vendidos por $4 a libra. Orlando quer fazer 30 libras de mistura de festa a um custo de $6,50 a libra, quantos quilos de nozes e quantos quilos de quadrados de cereais ele deve usar?

Resposta: 5 libras de quadrados de cereais, 25 libras de nozes

Experimente$\PageIndex{14}$

Becca quer misturar suco de frutas e refrigerante para dar um ponche. Ela pode comprar suco de frutas por $3 o galão e refrigerante por $4 o galão. Se ela quiser fazer 28 galões de ponche a um custo de $3,25 o galão, quantos galões de suco de frutas e quantos galões de refrigerante ela deve comprar?

Resposta: 21 galões de ponche de frutas, 7 galões de refrigerante

Também podemos usar o modelo de mistura para resolver problemas de investimento usando juros simples. Usamos a fórmula de juros simples,$I=Prt$, onde$t$ representamos o número de anos. Quando só precisamos encontrar o interesse por um ano$t=1$, então$I=Pr$.

Exemplo$\PageIndex{8}$

Stacey tem $20.000 para investir em duas contas bancárias diferentes. Uma conta paga juros a 3% ao ano e a outra conta paga juros a 5% ao ano. Quanto ela deve investir em cada conta se quiser ganhar 4,5% de juros ao ano sobre o valor total?

Solução

Preencheremos um gráfico para organizar nossas informações. Usaremos a fórmula simples de juros para encontrar os juros ganhos nas diferentes contas.

Os juros sobre o investimento misto virão da soma dos juros da conta que ganha 3% e os juros da conta ganhando 5% para obter os juros totais sobre os $20.000.

\[\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}\]

O valor investido é o principal de cada conta.

Nós inserimos a taxa de juros de cada conta.

Multiplicamos o valor investido pela taxa para obter os juros.

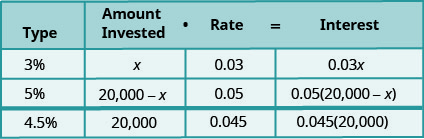
$Essa tabela tem quatro linhas e quatro colunas. A linha superior é uma linha de cabeçalho que diz da esquerda para a direita Tipo, Valor investido, Taxa e Juros. A segunda linha diz 3%, x, 0,03 e 0,03x. A terceira linha diz 5%, 20.000 menos x, 0,05 e 0,05 vezes a quantidade (20.000 menos x). A quarta linha diz 4,5%, 20.000, 0,045 e 0,045 vezes 20.000.$

Observe que o valor total investido, 20.000, é a soma do valor investido em 3% e do valor investido em 5%. E o total de juros,$0.045(20,000)$, é a soma dos juros auferidos na conta de 3% e dos juros auferidos na conta de 5%.

Assim como nas outras aplicações de mistura, a última coluna na tabela nos fornece a equação a ser resolvida.

Escreva a equação a partir dos juros ganhos. Resolva a equação.	$\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}$
Encontre o valor investido em 5%.	$.$ $.$ $.$
Verifique. $\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}$
	Stacey deve investir $5.000 na conta que ganha 3% e $15.000 na conta que ganha 5%.

Experimente$\PageIndex{15}$

Remy tem $14.000 para investir em dois fundos mútuos. Um fundo paga juros a 4% ao ano e o outro fundo paga juros a 7% ao ano. Quanto ela deve investir em cada fundo se quiser ganhar 6,1% de juros sobre o valor total?

Resposta: $4.200 a 4%, $9.800 a 7%

Experimente$\PageIndex{16}$

Marco tem $8.000 para economizar para a educação universitária de sua filha. Ele quer dividi-la entre uma conta que paga 3,2% de juros ao ano e outra conta que paga 8% de juros ao ano. Quanto ele deve investir em cada conta se quiser que os juros sobre o investimento total sejam de 6,5%?

Resposta: $2.500 a 3,2%, $5.500 a 8%

Conceitos-chave

Valor total das moedas Para o mesmo tipo de moeda, o valor total de várias moedas é encontrado usando o modelo.
número·valor=valor total onde número é o número de moedas e valor é o valor de cada moeda; valor total é o valor total de todas as moedas
Estratégia de resolução de problemas — problemas com a palavra moeda
1. Leia o problema. Faça com que todas as palavras e ideias sejam compreendidas. Determine os tipos de moedas envolvidas.
  - Crie uma tabela para organizar as informações.
  - Identifique as colunas como tipo, número, valor e valor total.
  - Liste os tipos de moedas.
  - Escreva o valor de cada tipo de moeda.
  - Escreva o valor total de todas as moedas.
2. Identifique o que estamos procurando.
3. Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
  Use expressões variáveis para representar o número de cada tipo de moeda e escrevê-las na tabela.
  Multiplique o número vezes o valor para obter o valor total de cada tipo de moeda.
4. Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em uma equação.
  Escreva a equação adicionando os valores totais de todos os tipos de moedas.
5. Resolva a equação usando boas técnicas de álgebra.
6. Verifique a resposta do problema e verifique se faz sentido.
7. Responda à pergunta com uma frase completa.

Glossário

problemas de mistura: Os problemas de mistura combinam dois ou mais itens com valores diferentes.

Nota

VALOR TOTAL DAS MOEDAS

Exemplo\(\PageIndex{1}\)

Experimente\(\PageIndex{1}\)

Experimente\(\PageIndex{2}\)

RESOLVA PROBLEMAS DE PALAVRAS-MOEDAS

Exemplo\(\PageIndex{2}\)

Experimente\(\PageIndex{3}\)

Experimente\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Experimente\(\PageIndex{5}\)

Experimente\(\PageIndex{6}\)

Exemplo\(\PageIndex{4}\)

Experimente\(\PageIndex{7}\)

Experimente\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Experimente\(\PageIndex{9}\)

Experimente\(\PageIndex{10}\)

Exemplo\(\PageIndex{6}\)

Experimente\(\PageIndex{11}\)

Experimente\(\PageIndex{12}\)

Exemplo\(\PageIndex{7}\)

Experimente\(\PageIndex{13}\)

Experimente\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Experimente\(\PageIndex{15}\)

Experimente\(\PageIndex{16}\)

Escreva a equação a partir dos juros ganhos. Resolva a equação.	\(\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}\)
Encontre o valor investido em 5%.	$.$ $.$ $.$
Verifique. \(\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}\)
	Stacey deve investir $5.000 na conta que ganha 3% e $15.000 na conta que ganha 5%.