3.2: Resolver aplicações percentuais
- Page ID
- 184298
Ao final desta seção, você poderá:
- Traduza e resolva equações percentuais básicas
- Solucione a porcentagem de aplicativos
- Encontre aumento percentual e redução percentual
- Resolva solicitações de juros simples
- Resolva aplicativos com desconto ou margem de lucro
Antes de começar, faça este teste de prontidão.
- Converta 4,5% em um decimal.
Se você perdeu esse problema, revise [link]. - Converta 0,6 em um por cento.
Se você perdeu esse problema, revise [link]. - Arredonde 0,875 para o centésimo mais próximo.
Se você perdeu esse problema, revise [link]. - Multiplique (4,5) (2,38).
Se você perdeu esse problema, revise [link]. - Resolva 3,5 = 0,7 m.
Se você perdeu esse problema, revise [link]. - Subtraia de 50 a 37,45.
Se você perdeu esse problema, revise [link].
Traduza e resolva equações percentuais básicas
Resolveremos equações percentuais usando os métodos que usamos para resolver equações com frações ou decimais. Sem as ferramentas da álgebra, o melhor método disponível para resolver problemas percentuais era configurá-los como proporções. Agora, como estudante de álgebra, você pode simplesmente traduzir frases em inglês em equações algébricas e depois resolver as equações.
Podemos usar qualquer letra que você quiser como variável, mas é uma boa ideia escolher uma letra que nos lembre do que você está procurando. Devemos ter certeza de alterar a porcentagem dada para um decimal ao colocá-la na equação.
Traduzir e resolver: Qual número é 35% de 90?
- Responda
-
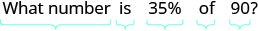
Traduza em álgebra. Seja n= o número. 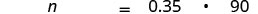
Lembre-se de que “de” significa multiplicar, “é” significa igual. Multiplique. 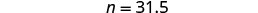
31,5 é 35% de 90
Traduza e resolva:
Qual número é 45% de 80?
- Responda
-
36
Traduza e resolva:
Qual número é 55% de 60?
- Responda
-
33
Devemos ter muito cuidado ao traduzir as palavras do próximo exemplo. A quantidade desconhecida não será isolada no início, como no Exemplo. Usaremos novamente a tradução direta para escrever a equação.
Traduza e resolva: 6,5% de qual número é $1,17?
- Responda
-

Traduzir. Seja n= o número. 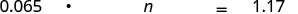
Multiplique. 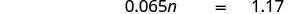
Divida os dois lados por 0,065 e simplifique. 
6,5% de $18 é $1,17
Traduza e resolva:
7,5% de qual número é $1,95?
- Responda
-
$26
Traduza e resolva:
8,5% de qual número é $3,06?
- Responda
-
$36
No próximo exemplo, estamos procurando a porcentagem.
Traduzir e resolver: 144 é qual a porcentagem de 96?
- Responda
-
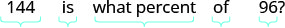
Traduza em álgebra. Seja p = a porcentagem. 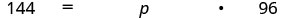
Multiplique. 
Divida por 96 e simplifique. 
Converta em porcentagem. 
144 é 150% de 96 Observe que somos solicitados a encontrar a porcentagem, então devemos ter nosso resultado final na forma de porcentagem.
Traduza e resolva:
110 é qual porcentagem de 88?
- Responda
-
125%
Traduza e resolva:
126 é qual porcentagem de 72?
- Responda
-
175%
Resolva aplicações de porcentagem
Muitas aplicações de porcentagem — como gorjetas, impostos sobre vendas, descontos e juros — ocorrem em nossas vidas diárias. Para resolver esses aplicativos, vamos traduzir em uma equação percentual básica, assim como as que resolvemos nos exemplos anteriores. Depois de traduzirmos a frase em uma equação percentual, sabemos como resolvê-la.
Vamos reafirmar a estratégia de resolução de problemas que usamos anteriormente para facilitar a referência.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação algébrica.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Agora que temos a estratégia a que nos referir e praticamos a solução de equações percentuais básicas, estamos prontos para resolver aplicações percentuais. Não deixe de se perguntar se sua resposta final faz sentido. Como muitos dos aplicativos envolvem situações cotidianas, você pode confiar em sua própria experiência.
Dezohn e sua namorada desfrutaram de um bom jantar em um restaurante e sua conta foi de $68,50. Ele quer deixar uma gorjeta de 18%. Se a gorjeta for 18% do total da conta, quanta gorjeta ele deve deixar?
- Responda
-
Observe que usamos t para representar a dica desconhecida.Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. a quantidade de gorjeta que Dezohn deve deixar Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Seja t = quantidade de gorjeta. Etapa 4. Traduza em uma equação. 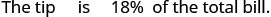
Escreva uma frase que forneça as informações para encontrá-la. 
Traduza a frase em uma equação. 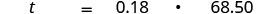
Etapa 5. Resolva a equação. Multiplique. 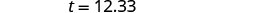
Etapa 6. Verifique. Isso faz sentido? Sim, 20% de $70 são $14. Etapa 7. Responda à pergunta com uma frase completa. Dezohn deve deixar uma gorjeta de $12,33.
Cierra e sua irmã jantaram em um restaurante e a conta foi de $81,50. Se ela quiser deixar 18% da conta total como gorjeta, quanto ela deve deixar?
- Responda
-
$14,67
Kimngoc almoçou em seu restaurante favorito. Ela quer deixar 15% da conta total como gorjeta. Se a conta dela fosse de $14,40, quanto ela deixaria para a gorjeta?
- Responda
-
$2,16
O rótulo do cereal matinal Masao diz que uma porção de cereal fornece 85 miligramas (mg) de potássio, que é 2% da quantidade diária recomendada. Qual é a quantidade diária total recomendada de potássio?
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. a quantidade total de potássio recomendada Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Deixe a= quantidade total de potássio. Etapa 4. Traduzir. Escreva uma frase que forneça as informações para encontrá-la. 
Traduza em uma equação. 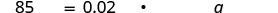
Etapa 5. Resolva a equação. 
Etapa 6. Verifique. Isso faz sentido? Sim, 2% é uma pequena porcentagem e 85 é uma pequena parte de 4.250. Etapa 7. Responda à pergunta com uma frase completa. A quantidade de potássio recomendada é de 4.250 mg.
Uma porção de cereal quadrado de trigo contém sete gramas de fibra, o que representa 28% da quantidade diária recomendada. Qual é a quantidade diária total recomendada de fibra?
- Responda
-
25 gramas
Uma porção de cereal de arroz contém 190 mg de sódio, o que representa 8% da quantidade diária recomendada. Qual é a quantidade diária total recomendada de sódio?
- Responda
-
2.375 mg
Mitzi recebeu alguns brownies gourmet de presente. A embalagem dizia que cada brownie tinha 480 calorias e 240 calorias de gordura. Qual porcentagem do total de calorias em cada brownie vem da gordura?
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. a porcentagem do total de calorias da gordura Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Deixe p= porcentagem de gordura. Etapa 4. Traduzir. Escreva uma frase que forneça as informações para encontrá-la. 
Traduza em uma equação. 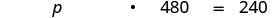
Etapa 5. Resolva a equação. 
Divida por 480. 
Coloque em um formulário percentual. 
Etapa 6. Verifique. Isso faz sentido? Sim, 240 é metade de 480, então 50% faz sentido. Etapa 7. Responda à pergunta com uma frase completa. Do total de calorias em cada brownie, 50% é gordura.
Resolver. Arredonde para a porcentagem inteira mais próxima.
Veronica está planejando fazer muffins a partir de uma mistura. O pacote diz que cada muffin terá 230 calorias e 60 calorias serão de gordura. Qual porcentagem do total de calorias é proveniente da gordura?
- Responda
-
26%
Resolver. Arredonde para a porcentagem inteira mais próxima.
A mistura que Ricardo planeja usar para fazer brownies diz que cada brownie terá 190 calorias e 76 calorias são de gordura. Qual a porcentagem do total de calorias provenientes da gordura?
- Responda
-
40%
Encontre aumento percentual e redução percentual
As pessoas na mídia costumam falar sobre o quanto uma quantia aumentou ou diminuiu em um determinado período de tempo. Eles geralmente expressam esse aumento ou diminuição em porcentagem.
Para encontrar o aumento percentual, primeiro encontramos o valor do aumento, a diferença entre o novo valor e o valor original. Em seguida, descobrimos qual é a porcentagem do valor do aumento do valor original.
- Encontre a quantidade de aumento.
\(\text{new amount }−\text{ original amount }=\text{ increase}\) - Encontre o aumento percentual.
O aumento é qual a porcentagem do valor original?
Em 2011, o governador da Califórnia propôs aumentar as taxas das faculdades comunitárias de $26 por unidade para $36 por unidade. Encontre o aumento percentual. (Arredonde para o décimo de um por cento mais próximo.)
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. o aumento percentual Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Seja p=p= a porcentagem. Etapa 4. Traduzir. Escreva uma frase que forneça as informações para encontrá-la. Primeiro, encontre a quantidade de aumento. novo valor − valor original = aumento 36−26 = 10 Encontre a porcentagem. O aumento é qual a porcentagem do valor original? 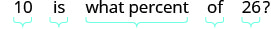
Traduza em uma equação. 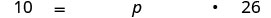
Etapa 5. Resolva a equação. 
Divida por 26. 
Mude para a forma percentual; arredonde para o décimo mais próximo. 
Etapa 6. Verifique. Isso faz sentido? Sim, 38,4% está próximo e 10 está próximo\(\frac{1}{3}\) de 26.\(\frac{1}{3}\) Etapa 7. Responda à pergunta com uma frase completa. As novas taxas representam um aumento de 38,4% em relação às taxas antigas.
Encontre o aumento percentual. (Arredonde para o décimo de um por cento mais próximo.)
Em 2011, o IRS aumentou o custo da quilometragem dedutível para 55,5 centavos de 51 centavos.
- Responda
-
8,8%
Encontre o aumento percentual.
Em 1995, a tarifa padrão de ônibus em Chicago era de $1,50. Em 2008, a tarifa padrão de ônibus foi de $2,25.
- Responda
-
50%
Encontrar a redução percentual é muito semelhante a encontrar o aumento percentual, mas agora a quantidade de redução é a diferença entre o valor original e o novo valor. Em seguida, descobrimos qual é a porcentagem da redução do valor original.
- Encontre a quantidade de diminuição.
\(\text{original amount }−\text{ new amount }=\text{ decrease}\) - Encontre a redução percentual.
A diminuição é qual a porcentagem do valor original?
O preço médio de um galão de gasolina em uma cidade em junho de 2014 foi de $3,71. O preço médio naquela cidade em julho foi de $3,64. Encontre a redução percentual.
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. a diminuição percentual Etapa 3. Diga o que estamos procurando. Escolha uma variável para representar essa quantidade. Permita que p= a porcentagem diminua. Etapa 4. Traduzir. Escreva uma frase que forneça as informações para encontrá-la. Primeiro, encontre a quantidade de diminuição. 3,71 −3,64 = 0,07 Encontre a porcentagem. Diminuir é qual a porcentagem do valor original? 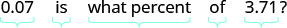
Traduza em uma equação. 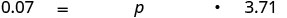
Etapa 5. Resolva a equação. 
Divida por 3,71. 
Mude para a forma percentual; arredonde para o décimo mais próximo. 
Etapa 6. Verifique. Isso faz sentido? Sim, se o preço original fosse de $4, uma redução de 2% seria de 8 centavos. Etapa 7. Responda à pergunta com uma frase completa. O preço do gás diminuiu 1,9%.
Encontre a redução percentual. (Arredonde para o décimo de um por cento mais próximo.)
A população da Dakota do Norte era de cerca de 672.000 em 2010. A população está projetada em cerca de 630.000 em 2020.
- Responda
-
6,3%
Encontre a redução percentual.
No ano passado, o salário de Sheila era de 42.000 dólares. Por causa dos dias de licença, este ano, seu salário foi de $37.800.
- Responda
-
10%
Resolva aplicativos de interesse simples
Você sabia que os bancos pagam para você ficar com seu dinheiro? O dinheiro que um cliente coloca no banco é chamado de principal, P, e o dinheiro que o banco paga ao cliente é chamado de juros. Os juros são calculados como uma certa porcentagem do principal; chamada de taxa de juros, r. Normalmente, expressamos a taxa de juros como uma porcentagem ao ano e a calculamos usando o equivalente decimal da porcentagem. A variável t, (por tempo) representa o número de anos em que o dinheiro está na conta.
Para encontrar o interesse, usamos a fórmula de juros simples, I = Prt.
Se uma quantia em dinheiro, P, chamada de principal, for investida por um período de t anos a uma taxa de juros anual r, a quantia de juros, I, ganha é
\[\begin{array}{lllll} {} &{} &{I} &{=} &{\text { interest }}\\ {I = Prt} &{\text{where}} &{P} &{=} &{\text { principle }}\\ {} &{} &{r} &{=} &{\text { rate }}\\ {} &{} &{t} &{=} &{\text { time }} \end{array}\]
Os juros ganhos de acordo com essa fórmula são chamados de juros simples.
Os juros também podem ser calculados de outra forma, chamados juros compostos. Esse tipo de interesse será abordado em aulas de matemática posteriores.
A fórmula que usamos para calcular juros simples é I = Prt. Para usar a fórmula, substituímos os valores que o problema nos fornece pelas variáveis e, em seguida, resolvemos a variável desconhecida. Pode ser útil organizar as informações em um gráfico.
Nathaly depositou $12.500 em sua conta bancária, onde ganhará 4% de juros. Quanto interesse Nathaly ganhará em 5 anos?
\[\begin{aligned} I &=? \\ P &=\$ 12,500 \\ r &=4 \% \\ t &=5 \text { years } \end{aligned}\]
- Responda
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of interest earned}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for.}} &{\text{Let I = the amount of interest.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{I = (12500)(.04)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{I = 2500} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {\qquad \text{Is } $2,500 \text{ is a reasonable interest} } &{} \\ {\qquad \text{on }$12,500? \text{ Yes.}} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The interest is }$2500} \\ {\text{complete sentence.}} &{} \ \end{array}\)
Areli investiu um principal de $950 em sua conta bancária com taxa de juros de 3%. Quanto de juros ela ganhou em 5 anos?
- Responda
-
$142,50
Susana investiu um principal de $36.000 em sua conta bancária com taxa de juros de 6,5%. Quanto de juros ela ganhou em 3 anos?
- Responda
-
$7020
Pode haver momentos em que sabemos o valor dos juros ganhos sobre um determinado principal durante um determinado período de tempo, mas não sabemos a taxa. Para encontrar a taxa, usamos a fórmula simples de juros, substituímos os valores fornecidos pelo principal e pelo tempo e, em seguida, resolvemos a taxa.
Loren emprestou a seu irmão $3.000 para ajudá-lo a comprar um carro. Em 4 anos, seu irmão lhe pagou de volta os $3.000 mais $660 em juros. Qual foi a taxa de juros?
\[\begin{array}{lll} {I} &{=} &{\$ 660} \\ {P} &{=} &{\$ 3000} \\ {r} &{=} &{?} \\ {t} &{=} &{4 \text { years } }\end{array}\]
- Responda
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the rate of interest}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. Choose}} &{\text{Let r = the rate of interest.}} \\ {\text{ a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{660 = (3000)r(4)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{660 = (12000)r} \\ {\text{Divide.}} &{0.055 = r} \\ {\text{Change to percent form.}} &{5.5\% = r} \\\\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {I = Prt} &{} \\ {660 \stackrel{?}{=} (3000)(0.055)(4)} &{} \\ {660 = 660\checkmark} &{} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The rate of interest was }5.5%} \\ {\text{complete sentence.}} &{} \end{array}\)
Observe que, neste exemplo, o irmão de Loren pagou juros a Loren, assim como um banco pagaria juros se Loren investisse seu dinheiro lá.
Jim emprestou à irmã $5.000 para ajudá-la a comprar uma casa. Em 3 anos, ela pagou a ele os $5.000, mais $900 de juros. Qual foi a taxa de juros?
- Responda
-
6%
Hang emprestou $7.500 de seus pais para pagar sua mensalidade. Em 5 anos, ela pagou a eles $1.500 de juros, além dos $7.500 emprestados. Qual foi a taxa de juros?
- Responda
-
4%
Eduardo percebeu que seus novos papéis de empréstimo de carro afirmavam que, com uma taxa de juros de 7,5%, ele pagaria $6.596,25 em juros em 5 anos. Quanto ele pediu emprestado para pagar seu carro?
- Responda
-
\(\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount borrowed (the principal)}} \\ {\text{a variable to represent that quantity.}} &{} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{Let P = principal borrowed.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{6596.25 = P(0.075)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{6596.25 = 0.375P} \\ {\text{Divide.}} &{17590 = P} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ {I = Prt} &{} \\ {6596.25 \stackrel{?}{=} (17590)(0.075)(5)} &{} \\ {6596.25 = 6596.25\checkmark} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The principal is }$17590} \\ {\text{complete sentence.}} &{} \ \end{array}\)
A nova declaração de empréstimo de carro de Sean disse que ele pagaria $4.866,25 em juros a partir de uma taxa de juros de 8,5% em 5 anos. Quanto ele pediu emprestado para comprar seu carro novo?
- Responda
-
$11.450
Em 5 anos, a conta bancária de Gloria ganhou $2.400 de juros a 5%. Quanto ela depositou na conta?
- Responda
-
$9.600
Resolva aplicativos com desconto ou margem
As aplicações de desconto são muito comuns em ambientes de varejo. Quando você compra um item à venda, o preço original foi descontado em algum valor em dólares. A taxa de desconto, geralmente dada como uma porcentagem, é usada para determinar o valor do desconto. Para determinar o valor do desconto, multiplicamos a taxa de desconto pelo preço original.
Resumimos o modelo de desconto na caixa abaixo.
\[\begin{array}{l}{\text { amount of discount }=\text { discount rate } \times \text { original price }} \\ {\text { sale price }=\text { original price - amount of discount }}\end{array}\]
Lembre-se de que o preço de venda deve ser sempre menor que o preço original.
Elise comprou um vestido com desconto de 35% sobre o preço original de $140. Qual foi ⓐ o valor do desconto e ⓑ o preço de venda do vestido?
- Responda
-
1. \(\begin{array} {lll} {\text{Original price}} &{=} &{$140} \\ {\text{Discount rate}} &{=} &{35\%} \\ {\text{Discount?}} &{=} &{?} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{} \\ {\text{Translate into an equation}} &{d = 0.35(140)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 49} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is a }$49\text{ discount reasonable for a}} &{} \\ {$140\text{ dress? Yes.}} &{} \\\\ {\textbf{Step 7. Write} \text{ a complete sentence to answer}} &{\text{The amount of discount was }$49} \\ {\text{the question.}} &{} \ \end{array}\)2.
Leia o problema novamente.Etapa 1. Identifique o que estamos procurando. o preço de venda do vestido Etapa 2. Diga o que estamos procurando. Escolha uma variável para representar essa quantidade. Seja s = o preço de venda. Etapa 3. Traduza em uma equação. Escreva uma frase que forneça as informações para encontrá-la. 
Traduza em uma equação. 
Etapa 4. Resolva a equação. 
Etapa 5. Verifique. Isso faz sentido? O preço de venda é menor do que o preço original? Sim, $91 é menos de $140. Etapa 6. Responda à pergunta com uma frase completa. O preço de venda do vestido foi de $91.
Encontre ⓐ o valor do desconto e ⓑ o preço de venda:
Sergio comprou um cinto com desconto de 40% em relação ao preço original de $29.
- Responda
-
ⓐ 11,60€ ⓑ 17,40€
Encontre ⓐ o valor do desconto e ⓑ o preço de venda:
Oscar comprou um churrasco que teve um desconto de 65% em relação ao preço original de $395.
- Responda
-
ⓐ $256,75 ⓑ $138,25
Pode haver momentos em que saibamos o preço original e o preço de venda e queremos saber a taxa de desconto. Para encontrar a taxa de desconto, primeiro encontraremos o valor do desconto e depois o usaremos para calcular a taxa como uma porcentagem do preço original. O exercício\(\PageIndex{37}\) mostrará esse caso.
Jeannette comprou um maiô a um preço de venda de $13,95. O preço original do maiô era de $31. Encontre o valor ⓐ do desconto e a taxa de desconto ⓑ.
- Responda
-
ⓐ\(\begin{array} {lll} {\text{Original price}} &{=} &{$31} \\ {\text{Discount}} &{=} &{?} \\ {\text{Sale Price}} &{=} &{$ 13.95} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{\text{The discount is the difference between the original}} \\ {} &{\text{price and the sale price.}} \\{\text{Translate into an equation}} &{d = 31 - 13.95} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 17.05} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is }17.05\text{ less than 31? Yes.}} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a complete sentence.}} &{\text{The amount of discount was }$17.05} \end{array}\)ⓑ
1. Quando traduzimos isso em uma equação, obtemos 17,05 igual a r vezes 31. Somos instruídos a resolver a equação 17.05 é igual a 31r. Dividimos por 31 para obter 0,55 igual a r. Colocamos isso em forma percentual para obter r igual a 55%. Somos instruídos a verificar: isso faz sentido? 7,05 é igual a 55% de >1? Abaixo disso, temos 17,05 iguais com um ponto de interrogação acima de 0,55 vezes 31. Abaixo disso, temos 17,05 igual a 17,05 com uma marca de seleção ao lado. Em seguida, somos instruídos a responder à pergunta com uma frase completa: A taxa de desconto foi de 55%.” >
Leia o problema novamente.Etapa 1. Identifique o que estamos procurando. a taxa de desconto Etapa 2. Diga o que estamos procurando. Escolha uma variável para representá-la. Seja r=r= a taxa de desconto. Etapa 3. Traduza em uma equação. Escreva uma frase que forneça as informações para encontrá-la. 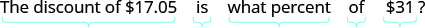
Traduza em uma equação. 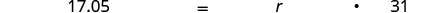
Etapa 4. Resolva a equação. 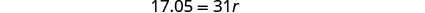
Divida os dois lados por 31. 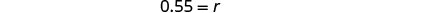
Alteração para o formulário percentual. 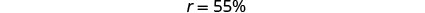
Etapa 5. Verifique. Isso faz sentido? $17,05 é igual a 55% de $31? \(17.05\stackrel{?}{=}0.55(31)\) \(17.05=17.05\checkmark\) Etapa 6. Responda à pergunta com uma frase completa. A taxa de desconto foi de 55%.
Encontre
- a quantidade de desconto e
- a taxa de desconto.
Lena comprou uma mesa de cozinha ao preço de venda de $375,20. O preço original da mesa era de $560.
- Responda
-
- $184,80
- 33%
Encontre
- a quantidade de desconto e
- a taxa de desconto.
Nick comprou um ar condicionado para vários quartos a um preço de venda de $340. O preço original do ar condicionado era de $400.
- Responda
-
- $60
- 15%
As aplicações de marcação são muito comuns em ambientes de varejo. O preço que um varejista paga por um item é chamado de custo original. O varejista então adiciona uma margem de lucro ao custo original para obter o preço sugerido, o preço pelo qual ele vende o item. A margem de lucro geralmente é calculada como uma porcentagem do custo original. Para determinar o valor da margem de lucro, multiplique a taxa de margem pelo custo original.
Resumimos o modelo de marcação na caixa abaixo.
\[\begin{array}{l}{\text { amount of mark-up }=\text { mark-up rate } \times \text { original cost }} \\ {\text { list price }=\text { original cost }+\text { amount of mark up }}\end{array}\]
Lembre-se de que o preço sugerido sempre deve ser maior do que o custo original.
A galeria de arte de Adam comprou uma fotografia pelo custo original de $250. Adam aumentou o preço em 40%. Encontre o
- quantidade de margem de lucro e
- o preço sugerido da fotografia.
- Responda
-
1.
2.Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. a quantidade de margem Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Seja m= a quantidade de marcação. Etapa 4. Traduza em uma equação. Escreva uma frase que forneça as informações para encontrá-la. 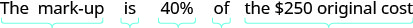
Traduza em uma equação. 
Etapa 5. Resolva a equação. 
Etapa 6. Verifique. Isso faz sentido? Sim, 40% é menos da metade e 100 é menos da metade de 250. Etapa 7. Responda à pergunta com uma frase completa. A margem na fotografia foi de $100. Etapa 1. Leia o problema novamente. Etapa 2. Identifique o que estamos procurando. o preço sugerido Etapa 3. Diga o que estamos procurando. Escolha uma variável para representá-la. Seja p = o preço sugerido. Etapa 4. Traduza em uma equação. Escreva uma frase que forneça as informações para encontrá-la. 
Traduza em uma equação. 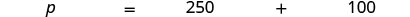
Etapa 5. Resolva a equação. 
Etapa 6. Verifique. Isso faz sentido? O preço sugerido é maior do que o preço líquido?
$350 é mais do que $250? Sim.Etapa 7. Responda à pergunta com uma frase completa. O preço sugerido da fotografia foi de $350.
Encontre
- a quantidade de margem e
- o preço sugerido.
A loja de música de Jim comprou uma guitarra ao custo original de $1.200. Jim aumentou o preço em 50%.
- Responda
-
- $600
- $1.800
Encontre
- a quantidade de margem e
- o preço sugerido.
A loja de revenda de automóveis comprou o Toyota de Pablo por $8.500. Eles aumentaram o preço em 35%.
- Responda
-
- $2.975
- $11.475
Conceitos chave
- Aumento percentual Para encontrar o aumento percentual:
- Encontre a quantidade de aumento. incremento=nova quantia−quantia originalaumente=nova quantia−quantia originalamount
- Encontre o aumento percentual. O aumento é qual a porcentagem do valor original?
- Diminuição percentual Para encontrar a redução percentual:
- Determine a quantidade de diminuição. diminuição=quantia original−novaquantiddiminue=quantia original−nova quantia
- Encontre a redução percentual. Diminuição é qual a porcentagem do valor original?
- Juros simples Se uma quantia em dinheiro, P, chamada de principal, for investida por um período de t anos a uma taxa de juros anual r, a quantia de juros, I, ganha é
\[\begin{aligned} I &=P r t \\ \text { where } I &=\text { interest } \\ P &=\text { principal } \\ r &=\text { rate } \\ t &=\text { time } \end{aligned}\]
- Desconto
- o valor do desconto é a taxa de desconto · preço original
- o preço de venda é o preço original — desconto
- Marcação
- quantidade de margem é taxa de margem · custo original
- o preço sugerido é o custo original + margem
Glossário
- quantidade de desconto
- O valor do desconto é o valor resultante quando uma taxa de desconto é multiplicada pelo preço original de um item.
- taxa de desconto
- A taxa de desconto é a porcentagem usada para determinar o valor de um desconto, comum em ambientes de varejo.
- interesse
- Juros são o dinheiro que um banco paga a seus clientes para manter seu dinheiro no banco.
- preço sugerido
- O preço sugerido é o preço pelo qual um varejista vende um item.
- marcação
- Uma margem de lucro é uma porcentagem do custo original usado para aumentar o preço de um item.
- custo original
- O custo original em um ambiente de varejo é o preço que um varejista paga por um item.
- diretor
- O principal é a quantia original de dinheiro investida ou emprestada por um período de tempo a uma taxa de juros específica.
- taxa de juros
- A taxa de juros é uma porcentagem do principal, geralmente expressa como uma porcentagem ao ano.
- juros simples
- Juros simples são os juros ganhos de acordo com a fórmula I = Prt.


