1.6: Visualize frações
- Page ID
- 184449
Ao final desta seção, você poderá:
- Encontre frações equivalentes
- Simplifique frações
- Multiplique frações
- Divida frações
- Simplifique expressões escritas com uma barra de fração
- Traduza frases em expressões com frações
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, Frações.
Encontre frações equivalentes
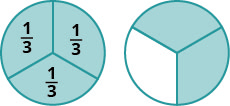
As frações são uma forma de representar partes de um todo. A fração\(\dfrac{1}{3}\) significa que um todo foi dividido em 3 partes iguais e cada parte é uma das três partes iguais. Veja a Figura\(\PageIndex{1}\). A fração\(\dfrac{2}{3}\) representa duas das três partes iguais. Na fração\(\dfrac{2}{3}\), o 2 é chamado de numerador e o 3 é chamado de denominador.
Uma fração é escrita\(\dfrac{a}{b}\), onde\(b\neq 0\) e
- \(a\)é o numerador e\(b\) é o denominador.
Uma fração representa partes de um todo. O denominador\(b\) é o número de partes iguais em que o todo foi dividido e o numerador\(a\) indica quantas partes estão incluídas.
Se uma torta inteira foi cortada em 6 pedaços e comemos todas as 6 peças, comemos\(\dfrac{6}{6}\) pedaços ou, em outras palavras, uma torta inteira.
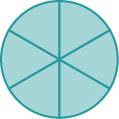
Então\(\dfrac{6}{6}=1\). Isso nos leva à propriedade de um que nos diz que qualquer número, exceto zero, dividido por si mesmo é\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
Qualquer número, exceto zero, dividido por si só é um.
Fazer a atividade de Matemática Manipulativa “Frações equivalentes a um” ajudará você a desenvolver uma melhor compreensão das frações que são equivalentes a uma.
Se uma torta foi cortada em 6 pedaços e comemos todas as 6, comemos\(\dfrac{6}{6}\) pedaços, ou, em outras palavras, uma torta inteira. Se a torta foi cortada em 8 pedaços e comemos todas as 8, comemos\(\dfrac{8}{8}\) pedaços ou uma torta inteira. Comemos a mesma quantidade: uma torta inteira.
As frações\(\dfrac{6}{6}\)\(\dfrac{8}{8}\) têm o mesmo valor, 1, e por isso são chamadas de frações equivalentes. Frações equivalentes são frações que têm o mesmo valor.
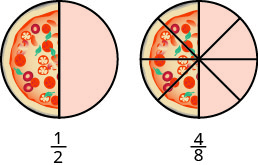
Vamos pensar em pizzas dessa vez. \(\PageIndex{3}\)A figura mostra duas imagens: uma única pizza à esquerda, cortada em dois pedaços iguais, e uma segunda pizza do mesmo tamanho, cortada em oito pedaços à direita. Essa é uma forma de mostrar que\(\dfrac{1}{2}\) é equivalente\(\dfrac{4}{8}\) a. Em outras palavras, são frações equivalentes.
Frações equivalentes são frações que têm o mesmo valor.
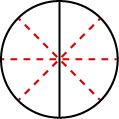
Como podemos usar a matemática para\(\dfrac{1}{2}\) nos transformar em\(\dfrac{4}{8}\)? Como podemos pegar uma pizza cortada em 2 pedaços e cortá-la em 8 pedaços? Poderíamos cortar cada um dos 2 pedaços maiores em 4 pedaços menores! A pizza inteira seria então cortada em 88 pedaços em vez de apenas 2. Matematicamente, o que descrevemos poderia ser escrito assim como\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). Veja a Figura\(\PageIndex{4}\).
Esse modelo leva à seguinte propriedade:
Se\(a,b,c\) são números onde\(b\neq 0, c\neq 0\), então
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
Se tivéssemos cortado a pizza de forma diferente, poderíamos obter
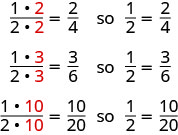
Então, dizemos que\(\dfrac{1}{2}\)\(\dfrac{2}{4}\),\(\dfrac{3}{6}\), e\(\dfrac{10}{20}\) são frações equivalentes.
Fazer a atividade de Matemática Manipulativa “Frações Equivalentes” ajudará você a desenvolver uma melhor compreensão do que significa quando duas frações são equivalentes.
Encontre três frações equivalentes\(\dfrac{2}{5}\) a.
- Resposta
-
Para encontrar uma fração equivalente a\(\dfrac{2}{5}\), multiplicamos o numerador e o denominador pelo mesmo número. Podemos escolher qualquer número, exceto zero. Vamos multiplicá-los por 2, 3 e depois 5.
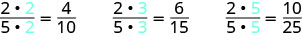
-
Então,\(\dfrac{4}{10}\),\(\dfrac{6}{15}\), e\(\dfrac{10}{25}\) são equivalentes\(\dfrac{2}{5}\) a.
Encontre três frações equivalentes\(\dfrac{3}{5}\) a.
- Resposta
-
\(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\); as respostas podem variar
Encontre três frações equivalentes\(\dfrac{4}{5}\) a.
- Resposta
-
\(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\); as respostas podem variar
Simplifique as frações
Uma fração é considerada simplificada se não houver fatores comuns, além de 1, em seu numerador e denominador.
Por exemplo,
- \(\dfrac{2}{3}\)é simplificado porque não há fatores comuns de 2 e 3.
- \(\dfrac{10}{15}\)não é simplificado porque 5 é um fator comum de 10 e 15.
Uma fração é considerada simplificada se não houver fatores comuns em seu numerador e denominador.
A frase reduzir uma fração significa simplificar a fração. Simplificamos ou reduzimos uma fração removendo os fatores comuns do numerador e do denominador. Uma fração não é simplificada até que todos os fatores comuns tenham sido removidos. Se uma expressão tiver frações, ela não será completamente simplificada até que as frações sejam simplificadas.
No Exercício\(\PageIndex{4}\), usamos a propriedade de frações equivalentes para encontrar frações equivalentes. Agora, usaremos a propriedade de frações equivalentes ao contrário para simplificar as frações. Podemos reescrever a propriedade para mostrar os dois formulários juntos.
Se\(a,b,c\) forem números em que\(b\neq 0,c\neq 0\),
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
Simplifique:\(-\dfrac{32}{56}\)
- Resposta
-
\(-\dfrac{32}{56}\) Reescreva o numerador e o denominador mostrando os fatores comuns. \(-\dfrac{4\cdot 8}{7\cdot 8}\) Simplifique usando a propriedade de frações equivalentes. \(-\dfrac{4}{7}\) Observe que a fração\(-\dfrac{4}{7}\) é simplificada porque não há mais fatores comuns.
Simplifique:\(-\dfrac{42}{54}\)
- Resposta
-
\(-\dfrac{7}{9}\)
Simplifique:\(-\dfrac{42}{54}\)
- Resposta
-
\(-\dfrac{5}{9}\)
Às vezes, pode não ser fácil encontrar fatores comuns do numerador e do denominador. Quando isso acontece, uma boa ideia é fatorar o numerador e o denominador em números primos s. Em seguida, divida os fatores comuns usando a propriedade de frações equivalentes.
Simplifique:\(-\dfrac{210}{385}\)
- Resposta
-



Simplifique:\(-\dfrac{69}{120}\)
- Resposta
-
\(-\dfrac{23}{40}\)
Simplifique:\(-\dfrac{120}{192}\)
- Resposta
-
\(-\dfrac{5}{8}\)
Agora resumimos as etapas que você deve seguir para simplificar as frações.
- Reescreva o numerador e o denominador para mostrar os fatores comuns.
Se necessário, primeiro fatore o numerador e o denominador em números primos. - Simplifique o uso da propriedade de frações equivalentes dividindo os fatores comuns.
- Multiplique os fatores restantes, se necessário.
Simplifique:\(\dfrac{5x}{5y}\)
- Resposta
-
\(\dfrac{5x}{5y}\) Reescreva mostrando os fatores comuns e depois divida os fatores comuns. 
Simplifique. \(\dfrac{x}{y}\)
Simplifique:\(\dfrac{7x}{7y}\)
- Resposta
-
\(\dfrac{x}{y}\)
Simplifique:\(\dfrac{3a}{3b}\)
- Resposta
-
\(\dfrac{a}{b}\)
Multiplique frações
Muitas pessoas acham mais fácil multiplicar e dividir frações do que somar e subtrair frações. Então, começaremos com a multiplicação de frações.
Fazer a atividade de Matemática Manipulativa “Multiplicação de Frações do Modelo” ajudará você a desenvolver uma melhor compreensão da multiplicação de frações.Usaremos um modelo para mostrar como multiplicar duas frações e para ajudá-lo a se lembrar do procedimento. Vamos começar com\(\dfrac{3}{4}\).

Agora vamos\(\dfrac{1}{2}\) decolar\(\dfrac{3}{4}\).

Note que agora, o todo está dividido em 8 partes iguais. Então\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
Para multiplicar frações, multiplicamos os numeradores e multiplicamos os denominadores.
Se\(a,b,c\) e\(d\) são números onde\(b\neq 0\) e\(d\neq 0\), então
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
Para multiplicar frações, multiplique os numeradores e multiplique os denominadores.
Ao multiplicar frações, as propriedades dos números positivos e negativos ainda se aplicam, é claro. É uma boa ideia determinar o sinal do produto como primeira etapa. No Exercício\(\PageIndex{13}\), multiplicaremos o negativo e o positivo, então o produto será negativo.
Multiplique:\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- Resposta
-
O primeiro passo é encontrar o sinal do produto. Como os sinais são diferentes, o produto é negativo.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
Multiplique:\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- Resposta
-
\(-\dfrac{4}{21}\)
Multiplique:\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- Resposta
-
\(-\dfrac{3}{16}\)
Ao multiplicar uma fração por um número inteiro, pode ser útil escrever o inteiro como uma fração. Qualquer número inteiro, a, pode ser escrito como\(\dfrac{a}{1}\). Então, por exemplo,\(3 = \dfrac{3}{1}\).
Multiplique:\(-\dfrac{12}{5}(-20x)\)
- Resposta
-
Determine o sinal do produto. Os sinais são os mesmos, então o produto é positivo.
\(-\dfrac{12}{5}(-20x)\) Escreva\(20x\) como uma fração. \(\dfrac{12}{5}(\dfrac{20x}{1})\) Multiplique. Reescreva\(20\) para mostrar o fator comum\(5\) e divida-o. 
Simplifique. \(48x\)
Multiplique:\(\dfrac{11}{3}(-9a)\)
- Resposta
-
\(-33a\)
Multiplique:\(\dfrac{13}{7}(-14b)\)
- Resposta
-
\(-26b\)
Divida frações
Agora que sabemos como multiplicar frações, estamos quase prontos para dividir. Antes de podermos fazer isso, precisamos de algum vocabulário.
O inverso de uma fração é encontrado invertendo a fração, colocando o numerador no denominador e o denominador no numerador. O recíproco de\(\dfrac{2}{3}\) é\(\dfrac{3}{2}\).
Observe isso\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). Um número e sua multiplicação recíproca para\(1\).
Para obter um produto positivo\(1\) ao multiplicar dois números, os números devem ter o mesmo sinal. Portanto, os recíprocos devem ter o mesmo sinal.
O recíproco de\(-\dfrac{10}{7}\) é\(-\dfrac{7}{10}\), desde\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
O recíproco de\(\dfrac{a}{b}\) é\(\dfrac{b}{a}\).
Um número e sua multiplicação recíproca por um\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
Fazer a atividade de Matemática Manipulativa “Divisão de Frações do Modelo” ajudará você a desenvolver uma melhor compreensão da divisão de frações.
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda.
Se\(a,b,c\) e\(d\) são números onde\(b\neq 0, c\neq 0\) e\(d\neq 0\), então
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda.
Precisamos dizer\(b\neq 0, c\neq 0\) e\(d\neq 0\) ter certeza de que não dividimos por zero!
Divida:\(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- Resposta
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
Divida:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- Resposta
-
\(-\dfrac{21}{5p}\)
Divida:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- Resposta
-
\(-\dfrac{15}{8q}\)
Encontre o quociente:
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- Resposta
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) Para dividir, multiplique a primeira fração pelo inverso da segunda. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) Determine o sinal do produto e multiplique.. \(\dfrac{7\cdot 27}{18\cdot 14}\) Reescreva mostrando fatores comuns. 
Remova os fatores comuns. \(\dfrac{3}{2\cdot 2}\) Simplifique. \(\dfrac{3}{4}\)
Encontre o quociente:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Resposta
-
\(\dfrac{4}{15}\)
Encontre o quociente:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Resposta
-
\(\dfrac{2}{3}\)
Há várias maneiras de lembrar quais etapas devem ser tomadas para multiplicar ou dividir frações. Uma maneira é repetir as chamadas para si mesmo. Se você fizer isso toda vez que fizer um exercício, terá as etapas memorizadas.
- “Para multiplicar frações, multiplique os numeradores e multiplique os denominadores.”
- “Para dividir frações, multiplique a primeira fração pelo inverso da segunda.”
Outra forma é manter dois exemplos em mente:
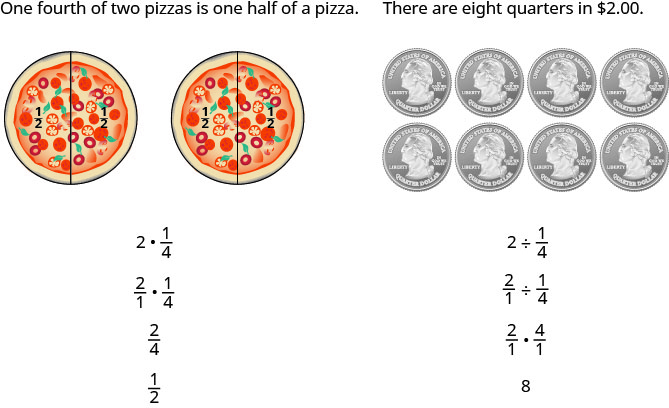
Os numeradores ou denominadores de algumas frações contêm as próprias frações. Uma fração na qual o numerador ou o denominador é uma fração é chamada de fração complexa.
Uma fração complexa é uma fração na qual o numerador ou o denominador contém uma fração.
Alguns exemplos de frações complexas são:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
Para simplificar uma fração complexa, lembramos que a barra de fração significa divisão. Por exemplo, a fração complexa\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) significa\(\dfrac{3}{4} \div \dfrac{5}{8}\).
Simplifique:\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- Resposta
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) Reescreva como divisão. \(\dfrac{3}{4} \div \dfrac{5}{8}\) Multiplique a primeira fração pelo inverso da segunda. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) Multiplique. \(\dfrac{3\cdot 8}{4\cdot 5}\) Procure fatores comuns. 
Divida os fatores comuns e simplifique. \(\dfrac{6}{5}\)
Simplifique:\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- Resposta
-
\(\dfrac{4}{5}\)
Simplifique:\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- Resposta
-
\(\dfrac{11}{14}\)
Simplifique:\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- Resposta
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) Reescreva como divisão. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) Multiplique a primeira fração pelo inverso da segunda. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) Multiplique. \(\dfrac{x\cdot 6}{2\cdot xy}\) Procure fatores comuns. 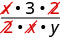
Divida os fatores comuns e simplifique. \(\dfrac{3}{y}\)
Simplifique:\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- Resposta
-
\(\dfrac{3}{4b}\)
Simplifique:\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- Resposta
-
\(\dfrac{4}{q}\)
Simplifique expressões com uma barra de fração
A linha que separa o numerador do denominador em uma fração é chamada de barra fracionária. Uma barra de fração atua como símbolo de agrupamento. A ordem das operações então nos diz para simplificar o numerador e depois o denominador. Em seguida, dividimos.
Para simplificar a expressão\(\dfrac{5 - 3}{7 + 1}\), primeiro simplificamos o numerador e o denominador separadamente. Em seguida, dividimos.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- Simplifique a expressão no numerador. Simplifique a expressão no denominador.
- Simplifique a fração.
Simplifique:\(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- Resposta
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
Simplifique:\(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- Resposta
-
\(-\dfrac{3}{4}\)
Simplifique:\(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- Resposta
-
\(-\dfrac{5}{3}\)
Para onde vai o sinal negativo em uma fração? Normalmente, o sinal negativo está na frente da fração, mas às vezes você verá uma fração com um numerador negativo ou às vezes com um denominador negativo. Lembre-se de que frações representam divisão. Quando o numerador e o denominador têm sinais diferentes, o quociente é negativo.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
Para quaisquer números positivos\(a\) e\(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
Simplifique:\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- Resposta
-
A barra de fração age como um símbolo de agrupamento. Portanto, simplifique completamente o numerador e o denominador separadamente.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
Simplifique:\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- Resposta
-
\(4\)
Simplifique:\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- Resposta
-
\(2\)
Traduza frases em expressões com frações
Agora que fizemos alguns trabalhos com frações, estamos prontos para traduzir frases que resultariam em expressões com frações.
As palavras em inglês quociente e razão são frequentemente usadas para descrever frações. Lembre-se de que “quociente” significa divisão. O quociente de aa e bb é o resultado que obtemos da divisão\(a\) por\(b\), ou\(\dfrac{a}{b}\).
Traduza a frase em inglês em uma expressão algébrica: o quociente da diferença de\( m\) e\(n\),\(p\) e.
- Resposta
-
Estamos procurando o quociente da diferença de\(m\) e\(n\), e\(p\).. Isso significa que queremos dividir a diferença de\(m\) e\(n\),\(p\) e.
\[\dfrac{m - n}{p}\]
Traduza a frase em inglês em uma expressão algébrica: o quociente da diferença de\(a\) e\(b\),\(cd\) e.
- Resposta
-
\(\dfrac{a - b}{cd}\)
Traduza a frase em inglês em uma expressão algébrica: o quociente da soma de\(p\) e\(q\),\(r\) e.
- Resposta
-
\(\dfrac{p + q}{r}\)
Conceitos chave
- Propriedade de frações equivalentes: Se\(a, b, c\) são números onde\(b\neq 0, c\neq 0\), então
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) e\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - Divisão de frações: se\(a, b, c\) e\(d\) são números onde\(b\neq 0, c\neq 0\) e\(d \neq 0\), então\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). Para dividir frações, multiplique a primeira fração pelo inverso da segunda.
- Multiplicação de frações: Se\(a,b,c\) e\(d\) são números onde\(b\neq 0, d\neq 0\), então\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). Para multiplicar frações, multiplique os numeradores e multiplique os denominadores.
- Colocação do sinal negativo em uma fração: Para qualquer número positivo\(a\) e\(b\),\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- Propriedade de Um:\(\dfrac{a}{a} = 1\) Qualquer número, exceto zero, dividido por si só é um.
- Simplifique uma fração
- Reescreva o numerador e o denominador para mostrar os fatores comuns. Se necessário, primeiro fatore o numerador e o denominador em números primos.
- Simplifique o uso da propriedade de frações equivalentes dividindo os fatores comuns.
- Multiplique todos os fatores restantes.
- Simplifique uma expressão com uma barra de fração
- Simplifique a expressão no numerador. Simplifique a expressão no denominador.
- Simplifique a fração.
Glossário
- fração complexa
- Uma fração complexa é uma fração na qual o numerador ou o denominador contém uma fração.
- denominador
- O denominador é o valor na parte inferior da fração que indica o número de partes iguais nas quais o todo foi dividido.
- frações equivalentes
- Frações equivalentes são frações que têm o mesmo valor.
- fração
- Uma fração é escrita\(\frac{a}{b}\), onde\(b\neq 0\), a é o numerador e b é o denominador. Uma fração representa partes de um todo. O denominador b é o número de partes iguais em que o todo foi dividido, e o numerador aa indica quantas partes estão incluídas.
- numerador
- O numerador é o valor na parte superior da fração que indica quantas partes do todo estão incluídas.
- recíproca
- O recíproco de\(\frac{a}{b}\) é\(\frac{b}{a}\). Um número e sua multiplicação recíproca por um:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- fração simplificada
- Uma fração é considerada simplificada se não houver fatores comuns em seu numerador e denominador.


