1.6E: Exercícios
- Page ID
- 184455
A prática leva à perfeição
Encontre frações equivalentes
Nos exercícios a seguir, encontre três frações equivalentes à fração dada. Mostre seu trabalho, usando figuras ou álgebra.
\(\dfrac{3}{8}\)
- Responda
-
\(\dfrac{6}{16}\),\(\dfrac{9}{24}\),\(\dfrac{12}{32}\), as respostas podem variar
\(\dfrac{5}{8}\)
\(\dfrac{5}{9}\)
- Responda
-
\(\dfrac{10}{18}\),\(\dfrac{15}{27}\),\(\dfrac{20}{36}\), as respostas podem variar
\(\dfrac{1}{8}\)
Simplifique as frações
Nos exercícios a seguir, simplifique.
\(-\dfrac{40}{88}\)
- Responda
-
\(-\dfrac{5}{11}\)
\(-\dfrac{63}{99}\)
\(-\dfrac{108}{63}\)
- Responda
-
\(-\dfrac{12}{7}\)
\(-\dfrac{104}{48}\)
\(\dfrac{120}{252}\)
- Responda
-
\(\dfrac{10}{21}\)
\(\dfrac{182}{294}\)
\(-\dfrac{3x}{12y}\)
- Responda
-
\(-\dfrac{x}{4y}\)
\(-\dfrac{4x}{32y}\)
\(\dfrac{14x^{2}}{21y}\)
- Responda
-
\(\dfrac{2x^{2}}{3y}\)
\(\dfrac{24a}{32b^{2}}\)
Multiplique frações
Nos exercícios a seguir, multiplique.
\(\dfrac{3}{4}\cdot \dfrac{9}{10}\)
- Responda
-
\(\dfrac{27}{40}\)
\(\dfrac{4}{5}\cdot \dfrac{2}{7}\)
\(-\dfrac{2}{3}\cdot -\dfrac{3}{8}\)
- Responda
-
\(\dfrac{1}{4}\)
\(-\dfrac{3}{4}\left(-\dfrac{4}{9}\right)\)
\(-\dfrac{5}{9}\cdot \dfrac{3}{10}\)
- Responda
-
\(-\dfrac{1}{6}\)
\(-\dfrac{3}{8}\cdot \dfrac{4}{15}\)
\(\left(-\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)
- Responda
-
\(-\dfrac{21}{50}\)
\(\left(-\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)
\(\left(-\dfrac{63}{84}\right)\left(-\dfrac{44}{90}\right)\)
- Resposta
-
\(\dfrac{11}{30}\)
\(\left(-\dfrac{63}{60}\right)\left(-\dfrac{40}{88}\right)\)
\(4\cdot \dfrac{5}{11}\)
- Resposta
-
\(\dfrac{20}{11}\)
\(5\cdot \dfrac{8}{3}\)
\(\dfrac{3}{7}\cdot 21n\)
- Resposta
-
9n
\(\dfrac{5}{6}\cdot 30m\)
\(-8\cdot\dfrac{17}{4}\)
- Resposta
-
−34
\((-1)\left(-\dfrac{6}{7}\right)\)
Divida frações
Nos exercícios a seguir, divida.
\(\dfrac{3}{4}\div \dfrac{2}{3}\)
- Resposta
-
\(\dfrac{9}{8}\)
\(\dfrac{4}{5}\div \dfrac{3}{4}\)
\(-\dfrac{7}{9}\div \left(-\dfrac{7}{4}\right)\)
- Resposta
-
1
\(-\dfrac{5}{6}\div \left(-\dfrac{5}{6}\right)\)
\(\dfrac{3}{4}\div \dfrac{x}{11}\)
- Resposta
-
\(\dfrac{33}{4x}\)
\(\dfrac{2}{5}\div \dfrac{y}{9}\)
\(\dfrac{5}{18}\div -\dfrac{15}{24}\)
- Resposta
-
\(-\dfrac{4}{9}\)
\(\dfrac{7}{18}\div \left(-\dfrac{14}{27}\right)\)
\(\dfrac{8u}{15} \div \dfrac{12v}{25}\)
- Resposta
-
\(\dfrac{10u}{9v}\)
\(\dfrac{12r}{25}\div \dfrac{18s}{35}\)
\(-5\div \dfrac{1}{2}\)
- Resposta
-
-10
\(-3\div \dfrac{1}{4}\)
\(\dfrac{3}{4}\div (-12)\)
- Resposta
-
\(\dfrac{1}{16}\)
\(-15\div -\dfrac{5}{3}\)
Nos exercícios a seguir, simplifique.
\(\dfrac{-\dfrac{8}{21}}{\dfrac{12}{35}}\)
- Resposta
-
\(-\dfrac{10}{9}\)
\(\dfrac{-\dfrac{9}{16}}{\dfrac{33}{40}}\)
\(\dfrac{-\dfrac{4}{5}}{2}\)
- Resposta
-
\(-\dfrac{2}{5}\)
\(\dfrac{5}{\dfrac{3}{10}}\)
\(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)
- Resposta
-
\(\dfrac{2m}{3n}\)
\(\dfrac{-\dfrac{3}{8}}{-\dfrac{y}{12}}\)
Simplifique expressões escritas com uma barra de fração
Nos exercícios a seguir, simplifique.
\(\dfrac{22 + 3}{10}\)
- Resposta
-
\(\dfrac{5}{2}\)
\(\dfrac{19 - 4}{6}\)
\(\dfrac{48}{24 - 15}\)
- Resposta
-
\(\dfrac{16}{3}\)
\(\dfrac{46}{4 + 4}\)
\(\dfrac{-6 + 6}{8 + 4}\)
- Resposta
-
0
\(\dfrac{-6 + 3}{17 - 8}\)
\(\dfrac{4\cdot 3}{6\cdot 6}\)
- Resposta
-
\(\dfrac{1}{3}\)
\(\dfrac{6\cdot 6}{9\cdot 2}\)
\(\dfrac{4^{2} - 1}{25}\)
- Resposta
-
\(\dfrac{3}{5}\)
\(\dfrac{7^{2} + 1}{60}\)
\(\dfrac{8\cdot 3 + 2\cdot 9}{14 + 3}\)
- Resposta
-
\(2\dfrac{8}{17}\)
\(\dfrac{9\cdot 6 - 4\cdot 7}{22 + 3}\)
\(\dfrac{5\cdot 6 - 3\cdot 4}{4\cdot 5 -2\cdot 3}\)
- Resposta
-
\(\dfrac{9}{7}\)
\(\dfrac{8\cdot 9 - 7\cdot 6}{5\cdot 6 - 9\cdot 2}\)
\(\dfrac{5^{2} - 3^{2}}{3 - 5}\)
- Resposta
-
\(-8\)
\(\dfrac{6^{2} - 4^{2}}{4 - 6}\)
\(\dfrac{7\cdot 4 - 2(8 - 5)}{9\cdot 3 - 3\cdot 5}\)
- Resposta
-
\(\dfrac{11}{6}\)
\(\dfrac{9\cdot 7 - 3(12- 8)}{8\cdot 7- 6\cdot 6}\)
\(\dfrac{9(8-2)-3(15-7)}{6(7-1) - 3(17-9)}\)
- Resposta
-
\(\dfrac{5}{2}\)
\(\dfrac{8(9-2) - 4(14 - 9)}{7(8-3)-3(16 -9)}\)
Traduza frases em expressões com frações
Nos exercícios a seguir, traduza cada frase em inglês em uma expressão algébrica.
o quociente de\(r\) e a soma de\(s\) e\(10\)
- Resposta
-
\(\dfrac{r}{s + 10}\)
o quociente de\(A\) e a diferença de\(3\) e\(B\)
o quociente da diferença de\(x\) e\(y\), e\(−3\)
- Resposta
-
\(\dfrac{x - y}{-3}\)
o quociente da soma de\(m\) e\(n\), e\(4q\)
Matemática diária
Cozimento. Uma receita de biscoitos de chocolate exige uma\(\frac{3}{4}\) xícara de açúcar mascavo. Imelda quer dobrar a receita.
- De quanto açúcar mascavo Imelda precisará? Mostre seu cálculo.
- Os copos medidores geralmente vêm em conjuntos de\(\frac{1}{4}\)\(\frac{1}{3}\),\(\frac{1}{2}\), e\(1\) copo. Faça um diagrama para mostrar duas maneiras diferentes de Imelda medir o açúcar mascavo necessário para dobrar a receita do biscoito.
- Resposta
-
- \(1\frac{1}{2}\)copos
- as respostas variarão
Cozimento. Nina está fazendo 4 panelas de chocolate para servir depois de um recital de música. Para cada panela, ela precisa de uma\(\frac{2}{3}\) xícara de leite condensado.
- Quanto leite condensado Nina precisará? Mostre seu cálculo.
- Os copos medidores geralmente vêm em conjuntos de\(\frac{1}{4}\)\(\frac{1}{3}\),\(\frac{1}{2}\), e\(1\) copo. Desenhe um diagrama para mostrar duas maneiras diferentes de Nina medir o leite condensado necessário para\(4\) panelas de chocolate.
Porções Don comprou um pacote a granel de doces que pesa\(5\) libras. Ele quer vender os doces em saquinhos com capacidade para\(\frac{1}{4}\) libras. Quantos saquinhos de doces ele pode encher da embalagem a granel?
- Resposta
-
\(20\)bolsas
Porções de Kristen tem\(\frac{3}{4}\) metros de fita que ela quer cortar em partes\(6\) iguais para fazer fitas de cabelo para as\(6\) bonecas de sua filha. Quanto tempo durará a fita de cabelo de cada boneca?
exercícios de escrita
Rafael queria pedir meia pizza média em um restaurante. O garçom disse a ele que uma pizza média poderia ser cortada\(6\) ou\(8\) fatiada. Ele preferiria\(3\) sem\(6\) fatias ou\(4\) sem\(8\) fatias? Rafael respondeu que, como não estava com muita fome,\(3\) preferia não usar\(6\) fatias. Explique o que há de errado com o raciocínio de Rafael.
- Resposta
-
As respostas podem variar
Dê um exemplo da vida cotidiana que demonstre como\(\dfrac{1}{2}\cdot \dfrac{2}{3}\) é\(\dfrac{1}{3}\).
Explique como você encontra o recíproco de uma fração.
- Resposta
-
As respostas podem variar
Explique como você encontra o inverso de um número negativo.
Verificação automática
ⓐ Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.
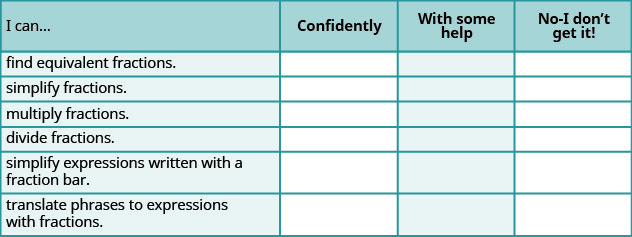
ⓑ Depois de ver a lista de verificação, você acha que está bem preparado para a próxima seção? Por que ou por que não?


