1.7: Adicionar e subtrair frações
- Page ID
- 184473
Ao final desta seção, você poderá:
- Adicione ou subtraia frações com um denominador comum
- Adicione ou subtraia frações com denominadores diferentes
- Use a ordem das operações para simplificar frações complexas
- Avalie expressões variáveis com frações
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, Frações.
Adicionar ou subtrair frações com um denominador comum
Quando multiplicamos frações, apenas multiplicamos os numeradores e multiplicamos os denominadores diretamente. Para somar ou subtrair frações, elas devem ter um denominador comum.
Se\(a,b\), e\(c\) são números onde\(c\neq 0\), então
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
Para adicionar ou subtrair frações, adicione ou subtraia os numeradores e coloque o resultado sobre o denominador comum.
Fazer as atividades de Matemática Manipulativa “Adição de Fração de Modelo” e “Subtração de Fração de Modelo” ajudará você a desenvolver uma melhor compreensão da adição e subtração de frações.
Encontre a soma:\(\dfrac{x}{3} + \dfrac{2}{3}\).
- Resposta
-
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
Encontre a soma:\(\dfrac{x}{4} + \dfrac{3}{4}\).
- Resposta
-
\(\dfrac{x + 3}{4}\)
Encontre a soma:\(\dfrac{y}{8} + \dfrac{5}{8}\).
- Resposta
-
\(\dfrac{y + 5}{8}\)
Descubra a diferença:\(-\dfrac{23}{24} - \dfrac{13}{24}\)
- Resposta
-
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
Descubra a diferença:\(-\dfrac{19}{28} - \dfrac{7}{28}\)
- Resposta
-
\(-\dfrac{26}{28}\)
Descubra a diferença:\(-\dfrac{27}{32} - \dfrac{1}{32}\)
- Resposta
-
\(-\dfrac{7}{8}\)
Descubra a diferença:\(-\dfrac{10}{x} - \dfrac{4}{x}\)
- Resposta
-
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
Descubra a diferença:\(-\dfrac{9}{x} - \dfrac{7}{x}\)
- Resposta
-
\(-\dfrac{16}{x}\)
Descubra a diferença:\(-\dfrac{17}{a} - \dfrac{5}{a}\)
- Resposta
-
\(-\dfrac{22}{a}\)
Simplifique:\(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
- Resposta
-
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
Simplifique:\(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Resposta
-
\(-1\)
Simplifique:\(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Resposta
-
\(-\dfrac{2}{3}\)
Adicione ou subtraia frações com denominadores diferentes
Como vimos, para somar ou subtrair frações, seus denominadores devem ser os mesmos. O denominador menos comum (LCD) de duas frações é o menor número que pode ser usado como denominador comum das frações. O LCD das duas frações é o mínimo múltiplo comum (LCM) de seus denominadores.
O menor denominador comum (LCD) de duas frações é o mínimo múltiplo comum (LCM) de seus denominadores.
Fazer a atividade de matemática manipulativa “Encontrar o denominador menos comum” ajudará você a desenvolver uma melhor compreensão do LCD.
Depois de encontrarmos o denominador menos comum de duas frações, convertemos as frações em frações equivalentes com o LCD. Juntar essas etapas nos permite somar e subtrair frações porque seus denominadores serão os mesmos!
Adicionar:\(\dfrac{7}{12} + \dfrac{5}{18}\)
- Resposta
-



Adicionar:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Resposta
-
\(\dfrac{79}{60}\)
Adicionar:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Resposta
-
\(\dfrac{103}{60}\)
- Eles têm um denominador comum?
- Sim, vá para a etapa 2.
- Não — reescreva cada fração com o LCD (denominador menos comum). Encontre o LCD. Altere cada fração em uma fração equivalente com o LCD como seu denominador.
- Adicione ou subtraia as frações.
- Simplifique, se possível.
Ao encontrar as frações equivalentes necessárias para criar os denominadores comuns, existe uma maneira rápida de encontrar o número necessário para multiplicar o numerador e o denominador. Esse método funciona se encontrarmos o LCD fatorando em números primos.
Veja os fatores do LCD e, em seguida, em cada coluna acima desses fatores. Os fatores “ausentes” de cada denominador são os números de que precisamos.

No Exercício\(\PageIndex{13}\), o LCD, 36, tem dois fatores de 2 e dois fatores de 3.
O numerador 12 tem dois fatores de 2, mas apenas um de 3 - então está “faltando” um 3 - multiplicamos o numerador e o denominador por 3.
O numerador 18 não tem um fator de 2 — então multiplicamos o numerador e o denominador por 2.
Aplicaremos esse método à medida que subtrairmos as frações no Exercício\(\PageIndex{16}\).
Subtrair:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Resposta
-
As frações têm um denominador comum? Não, então precisamos encontrar o LCD.
Encontre o LCD. 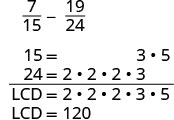
Observe que 15 está “faltando” três fatores de 2 e 24 está “faltando” os 5 dos fatores do LCD. Então, multiplicamos 8 na primeira fração e 5 na segunda fração para obter o LCD. Reescreva como frações equivalentes com o LCD. 
Simplifique. 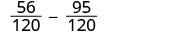
Subtrair. \(-\dfrac{39}{120}\) Verifique se a resposta pode ser simplificada. \(-\dfrac{13\cdot3}{40\cdot3}\) Tanto 39 quanto 120 têm um fator de 3. Simplifique. \(-\dfrac{13}{40}\) Não simplifique as frações equivalentes! Se fizer isso, você voltará às frações originais e perderá o denominador comum!
Subtrair:\(\dfrac{13}{24} - \dfrac{17}{32}\)
- Resposta
-
\(\dfrac{1}{96}\)
Subtrair:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Resposta
-
\(\dfrac{75}{224}\)
No próximo exemplo, uma das frações tem uma variável em seu numerador. Observe que fazemos as mesmas etapas de quando os dois numeradores são números.
Adicionar:\(\dfrac{3}{5} + \dfrac{x}{8}\)
- Resposta
-
As frações têm denominadores diferentes.
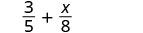
Encontre o LCD. 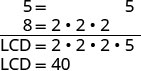
Reescreva como frações equivalentes com o LCD. 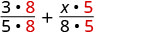
Simplifique. 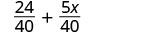
Adicionar. 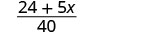
Lembre-se de que só podemos adicionar termos semelhantes:\(24\) e não\(5x\) são termos semelhantes.
Adicionar:\(\dfrac{y}{6} + \dfrac{7}{9}\)
- Resposta
-
\(\dfrac{3y + 14}{18}\)
Adicionar:\(\dfrac{x}{6} + \dfrac{7}{15}\)
- Responda
-
\(\dfrac{15x + 42}{153}\)
Agora temos todas as quatro operações para frações. A tabela\(\PageIndex{1}\) resume as operações de frações.
| Multiplicação de frações | Divisão de frações |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) Multiplique os numeradores e multiplique os denominadores |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) Multiplique a primeira fração pelo inverso da segunda. |
| Adição de frações | Subtração de frações |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Adicione os numeradores e coloque a soma sobre o denominador comum. |
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Subtraia os numeradores e coloque a diferença sobre o denominador comum. |
| Para multiplicar ou dividir frações, o LCD NÃO é necessário. Para adicionar ou subtrair frações, é necessário um LCD. | |
Simplifique:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
- Responda
-
Primeiro pergunte: “O que é a operação?” Depois de identificarmos a operação, isso determinará se precisamos de um denominador comum. Lembre-se de que precisamos de um denominador comum para somar ou subtrair, mas não para multiplicar ou dividir.
1. O que é a operação? A operação é subtração.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. O que é a operação? Multiplicação.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
Simplifique:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- Responda
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
Simplifique:
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- Responda
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
Use a ordem das operações para simplificar frações complexas
Vimos que uma fração complexa é uma fração na qual o numerato ou denominador contém uma fração. A barra de fração indica divisão. Simplificamos a fração\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) complexa dividindo\(\dfrac{3}{4}\) por\(\dfrac{5}{8}\).
Agora, veremos frações complexas em que o numerador ou denominador contém uma expressão que pode ser simplificada. Portanto, primeiro devemos simplificar completamente o numerador e o denominador separadamente usando a ordem das operações. Em seguida, dividimos o numerador pelo denominador.
Simplifique:\(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
- Responda
-



Simplifique:\(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- Responda
-
\(\dfrac{1}{90}\)
Simplifique:\(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- Responda
-
\(272\)
- Simplifique o numerador.
- Simplifique o denominador.
- Divida o numerador pelo denominador. Simplifique, se possível.
Simplifique:\(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
- Responda
-
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
Simplifique:\(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- Responda
-
\(2\)
Simplifique:\(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- Responda
-
\(\dfrac{2}{7}\)
Avalie expressões variáveis com frações
Já avaliamos expressões antes, mas agora podemos avaliar expressões com frações. Lembre-se de que, para avaliar uma expressão, substituímos o valor da variável na expressão e depois simplificamos.
Avalie\(x + \dfrac{1}{3}\) quando
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
- Responda
-
1. Para avaliar\(x + \dfrac{1}{3}\) quando\(x = -\dfrac{1}{3}\), substitua\(-\dfrac{1}{3}\) por\(x\) na expressão.
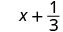
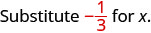
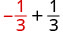
Simplifique. \(0\)
2. Para avaliar\(x + \dfrac{1}{3}\) quando\(x = -\dfrac{3}{4}\), substitua\(-\dfrac{3}{4}\) por\(x\) na expressão.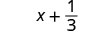

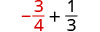
Reescreva como frações equivalentes com o LCD, 12. 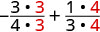
Simplifique. 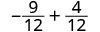
Adicionar. \(-\dfrac{5}{12}\)
Avalie\(x + \dfrac{3}{4}\) quando
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- Responda
-
- \(-1\)
- \(-\dfrac{1}{2}\)
Avalie\(y + \dfrac{1}{2}\) quando
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- Responda
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
Avalie\(-\dfrac{5}{6} - y\) quando\(y = -\dfrac{2}{3}\)
- Responda
-
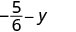
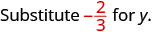
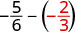
Reescreva como frações equivalentes com o LCD,\(6\). 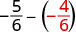
Subtrair. 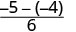
Simplifique. \(-\dfrac{1}{6}\)
Avalie\(y + \dfrac{1}{2}\) quando\(y = \dfrac{2}{3}\)
- Responda
-
\(-\dfrac{1}{4}\)
Avalie\(y + \dfrac{1}{2}\) quando\(y = \dfrac{2}{3}\)
- Responda
-
\(-\dfrac{17}{8}\)
Avalie\(2x^{2}y\) quando\(x = \dfrac{1}{4}\)\(y = -\dfrac{2}{3}\) e.
- Responda
-
Substitua os valores na expressão.
\(2x^{2}y\) 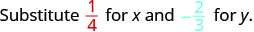
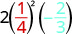
Simplifique primeiro os expoentes. \(2(\frac{1}{16})(-\frac{2}{3})\) Multiplique. Divida os fatores comuns. Observe\(16\) que escrevemos\(2\cdot2\cdot4\) para facilitar a remoção \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) Simplifique. \(-\frac{1}{12}\)
Avalie\(3ab^{2}\) quando\(a = -\dfrac{2}{3}\)\(b = -\dfrac{1}{2}\) e.
- Responda
-
\(-\dfrac{1}{2}\)
Avalie\(4c^{3}d\) quando\(c = -\dfrac{1}{2}\)\(d = -\dfrac{4}{3}\) e.
- Responda
-
\(\dfrac{2}{3}\)
O próximo exemplo terá apenas variáveis, sem constantes.
Avalie\(\dfrac{p + q}{r}\) quando\(p = -4, q = -2\),\(r = 8\) e.
- Responda
-
Para avaliar\(\dfrac{p + q}{r}\) quando e\(p = -4, q = -2\)\(r = 8\), substituímos os valores na expressão.
\(\dfrac{p + q}{r}\) 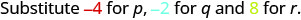
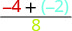
Adicione primeiro o numerador. \(\dfrac{-6}{8}\) Simplifique. \(-\dfrac{3}{4}\)
Avalie\(\dfrac{a+b}{c}\) quando\(a = -8, b = -7\),\(c = 6\) e.
- Responda
-
\(-\dfrac{5}{2}\)
Avalie\(\dfrac{x+y}{z}\) quando\(x = 9, y = -18\),\(z = -6\) e.
- Responda
-
\(\dfrac{3}{2}\)
Conceitos-chave
- Adição e subtração de frações: Se\(a, b\), e\(c\) são números onde\(c\neq 0\), então
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) e\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
Para adicionar ou subtrair frações, adicione ou subtraia os numeradores e coloque o resultado sobre o denominador comum.
- Estratégia para adicionar ou subtrair frações
- Eles têm um denominador comum?
Sim, vá para a etapa 2.
Não — Reescreva cada fração com o LCD (Least Common Denominator). Encontre o LCD. Altere cada fração em uma fração equivalente com o LCD como seu denominador. - Adicione ou subtraia as frações.
- Simplifique, se possível. Para multiplicar ou dividir frações, não é necessário um LCD. Para adicionar ou subtrair frações, é necessário um LCD.
- Eles têm um denominador comum?
- Simplifique frações complexas
- Simplifique o numerador.
- Simplifique o denominador.
- Divida o numerador pelo denominador. Simplifique, se possível.


