Skip to main content
Global

16.6E: Exercícios para a Seção 16.6

  1. Last updated
  2. Save as PDF
  • Page ID
    188482

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 4, determine se as afirmações são verdadeiras ou falsas.

    1. Se a superfície\(S\) for dada por\(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}\), então\(\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx \, dy.\)

    Resposta
    É verdade

    2. Se a superfície\(S\) for dada por\(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}\), então\(\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx \, dy.\)

    3. A superfície\(\vecs r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle,\) para\( 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) é a mesma superfície\(\vecs r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle,\) para\( 0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4\).

    Resposta
    É verdade

    4. Dada a parametrização padrão de uma esfera, os vetores normais\(t_u \times t_v\) são vetores normais externos.

    Nos exercícios 5 a 10, encontre descrições paramétricas para as seguintes superfícies.

    5. Avião\(3x - 2y + z = 2\)

    Resposta
    \(\vecs r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle \)para\(-\infty \leq u < \infty\)\( - \infty \leq v < \infty\) e.

    6. Parabolóide\(z = x^2 + y^2\), para\(0 \leq z \leq 9\).

    7. Avião\(2x - 4y + 3z = 16\)

    Resposta
    \(\vecs r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle \)para\(|u| < \infty\)\(|v| < \infty\) e.

    8. O tronco do cone\(z^2 = x^2 + y^2\), para\(2 \leq z \leq 8\)

    9. A porção do cilindro\(x^2 + y^2 = 9\) no primeiro octante, para\(0 \leq z \leq 3\)

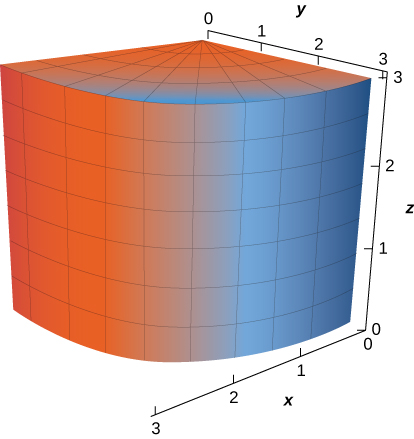
    Um diagrama em três dimensões de uma seção de um cilindro com raio 3. O centro de sua parte superior circular é (0,0,3). A seção existe para x, y e z entre 0 e 3.

    Resposta
    \(\vecs r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle \) for \(0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3\)

    10. A cone with base radius \(r\) and height \(h,\) where \(r\) and \(h\) are positive constants.

    For exercises 11 - 12, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.

    11. [T] Half cylinder \(\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}\)

    Answer
    \(A = 87.9646\)

    12. [T] Plane \(z = 10 - z - y\) above square \(|x| \leq 2, \, |y| \leq 2\)

    In exercises 13 - 15, let \(S\) be the hemisphere \(x^2 + y^2 + z^2 = 4\), with \(z \geq 0\), and evaluate each surface integral, in the counterclockwise direction.

    13. \(\displaystyle \iint_S z\, dS\)

    Answer
    \(\displaystyle \iint_S z \, dS = 8\pi\)

    14. \(\displaystyle \iint_S (x - 2y) \, dS\)

    15. \(\displaystyle \iint_S (x^2 + y^2) \, dS\)

    Answer
    \(\displaystyle \iint_S (x^2 + y^2) \, dS = 16 \pi\)

    In exercises 16 - 18, evaluate \(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS\) for vector field \(\vecs F\) where \(\vecs N\) is an outward normal vector to surface \(S.\)

    16. \(\vecs F(x,y,z) = x\,\mathbf{\hat i}+ 2y\,\mathbf{\hat j} = 3z\,\mathbf{\hat k}\), and \(S\) is that part of plane \(15x - 12y + 3z = 6\) that lies above unit square \(0 \leq x \leq 1, \, 0 \leq y \leq 1\).

    17. \(\vecs F(x,y) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j}\), and \(S\) is hemisphere \(z = \sqrt{1 - x^2 - y^2}\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{4\pi}{3}\)

    18. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}\), and \(S\) is the portion of plane \(z = y + 1\) that lies inside cylinder \(x^2 + y^2 = 1\).

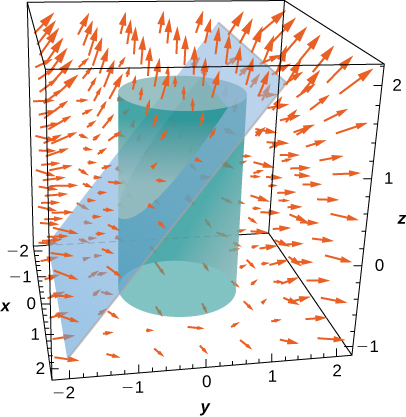
    A cylinder and an intersecting plane shown in three-dimensions. S is the portion of the plane z = y + 1 inside the cylinder x^2 + y ^2 = 1.

    Nos exercícios 19 a 20, aproxime a massa da lâmina homogênea que tem a forma de determinada superfície.\(S.\) Arredonde até quatro casas decimais.

    19. [T]\(S\) é superfície\(z = 4 - x - 2y\), com\(z \geq 0, \, x \geq 0, \, y \geq 0; \, \xi = x.\)

    Resposta
    \(m \approx 13.0639\)

    20. [T]\(S\) é superfície\(z = x^2 + y^2\), com\(z \leq 1; \, \xi = z\).

    21. [T]\(S\) é superfície\(x^2 + y^2 + x^2 = 5\), com\(z \geq 1; \, \xi = \theta^2\).

    Resposta
    \(m \approx 228.5313\)

    22. Avalie\(\displaystyle \iint_S (y^2 z\,\mathbf{\hat i}+ y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}) \cdot dS,\) onde\(S\) está a superfície do cubo\(-1 \leq x \leq 1, \, -1 \leq y \leq 1\) e\(0 \leq z \leq 2\) no sentido anti-horário.

    23. Avalie a integral da superfície\(\displaystyle \iint_S g \, dS,\) onde\(g(x,y,z) = xz + 2x^2 - 3xy\) e\(S\) é a parte do plano\(2x - 3y + z = 6\) que fica sobre a unidade quadrada\(R: 0 \leq x \leq 1, \, 0 \leq y \leq 1\).

    Resposta
    \(\displaystyle \iint_S g\,dS = 3 \sqrt{4}\)

    24. Avalie\(\displaystyle \iint_S (x + y + z)\, dS,\) onde\(S\) está a superfície definida parametricamente\(\vecs R(u,v) = (2u + v)\,\mathbf{\hat i} + (u - 2v)\,\mathbf{\hat j} + (u + 3v)\,\mathbf{\hat k}\) por for\(0 \leq u \leq 1\),\(0 \leq v \leq 2\) e.

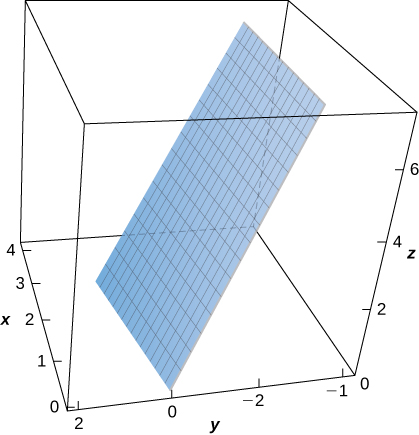
    Um diagrama tridimensional da superfície dada, que parece ser um plano inclinado acentuadamente que se estende pelo plano (x, y).

    25. [T] Avaliar\(\displaystyle \iint_S (x - y^2 + z)\, dS,\) where \(S\) is the surface defined parametrically by \(\vecs R(u,v) = u^2\,\mathbf{\hat i} + v\,\mathbf{\hat j} + u\,\mathbf{\hat k}\) for \(0 \leq u \leq 1, \, 0 \leq v \leq 1\).

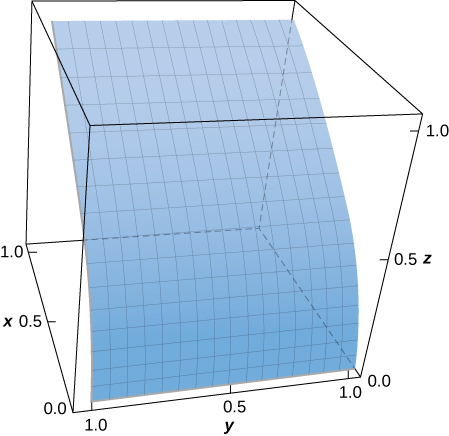
    A three-dimensional diagram of the given surface, which appears to be a curve with edges parallel to the y-axis. It increases in x components and decreases in z components the further it is from the y axis.

    Resposta
    \(\displaystyle \iint_S (x^2 + y - z) \, dS \approx 0.9617\)

    26. [T] Avalie onde\(S\) está a superfície definida\(\vecs R(u,v) = u\,\mathbf{\hat i} - u^2\,\mathbf{\hat j} + v\,\mathbf{\hat k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1\) por for\(0 \leq u \leq 1, \, 0 \leq v \leq 2\).

    27. Avalie\(\displaystyle \iint_S (x^2 + y^2) \, dS,\) onde\(S\) está a superfície delimitada acima do hemisfério\(z = \sqrt{1 - x^2 - y^2}\) e abaixo pelo plano\(z = 0\).

    Resposta
    \(\displaystyle \iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}\)

    28. Avalie\(\displaystyle \iint_S (x^2 + y^2 + z^2) \, dS,\) onde\(S\) está a parte do plano que está dentro do cilindro\(x^2 + y^2 = 1\).

    29. [T] Avalie\(\displaystyle \iint_S x^2 z \, dS,\) onde\(S\) está a parte do cone\(z^2 = x^2 + y^2\) que fica entre os planos\(z = 1\)\(z = 4\) e.

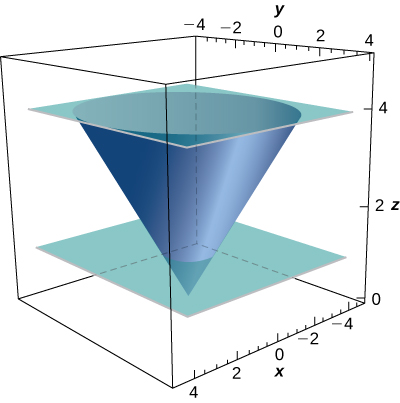
    Um diagrama do cone de abertura ascendente fornecido em três dimensões. O cone é cortado pelos planos z=1 e z=4.

    Resposta
    \(\text{div}\,\vecs F = a + b\)

    \(\displaystyle \iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}\)

    30. [T] Evaluate \(\displaystyle \iint_S \frac{xz}{y} \, dS,\) where \(S\) is the portion of cylinder \(x = y^2\) that lies in the first octant between planes \(z = 0, \, z = 5\), and \(y = 4\).

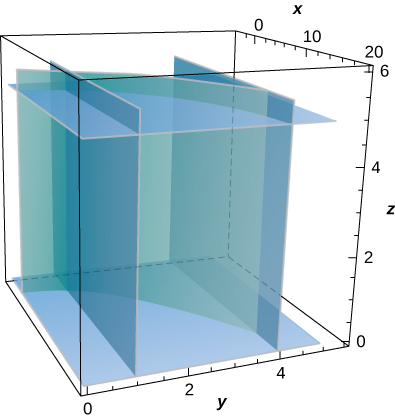
    A diagram of the given cylinder in three-dimensions. It is cut by the planes z=0, z=5, y=1, and y=4.

    31. [T] Avalie\(\displaystyle \iint_S (z + y) \, dS,\) onde\(S\) está a parte do gráfico de\( z = \sqrt{1 - x^2}\) na primeira octante entre o\(xy\) plano -e o plano\(y = 3\).

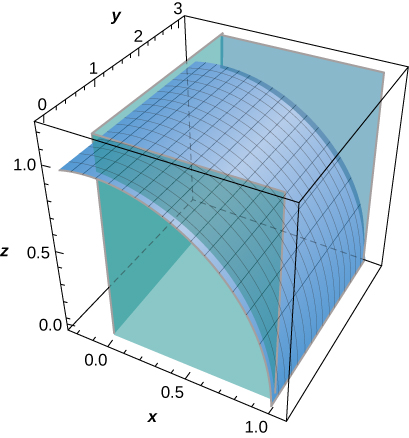
    Um diagrama da superfície dada em três dimensões na primeira octante entre o plano xz e o plano y=3. O gráfico dado de z= a raiz quadrada de (1-x^2) se estende para baixo em uma curva côncava descendente de ao longo (0, y,1) até along (1, y,0). Parece uma parte de um cilindro horizontal com base ao longo do plano xz e altura ao longo do eixo y.

    Resposta
    \(\displaystyle \iint_S (z + y) \, dS \approx 10.1\)

    32. Evaluate \(\displaystyle \iint_S xyz\, dS\) if \(S\) is the part of plane \(z = x + y\) that lies over the triangular region in the \(xy\)-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).

    33. Find the mass of a lamina of density \(\xi (x,y,z) = z\) in the shape of hemisphere \(z = (a^2 - x^2 - y^2)^{1/2}\).

    Answer
    \(m = \pi a^3\)

    34. Compute \(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} - 5y\,\mathbf{\hat j} + 4z\,\mathbf{\hat k}\) and \(\vecs N\) is an outward normal vector \(S,\) where \(S\) is the union of two squares \(S_1\) : \(x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) and \(S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1\).

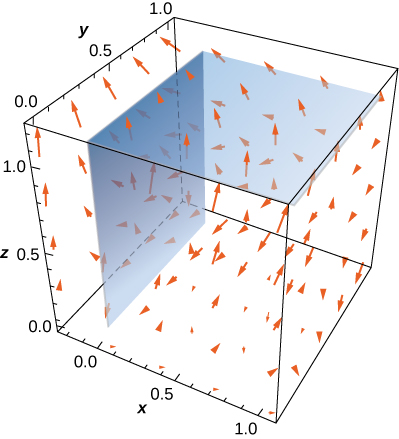
    A diagram in three dimensions. It shows the square formed by the components x=0, 0 <= y <= 1, and 0 <= z <= 1. It also shows the square formed by the components z=1, 0 <= x <= 1, and 0 <= y <= 1.

    35. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + z\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}\)Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) onde e\(\vecs N\) é um vetor normal externo\(S,\) onde\(S\) está a região triangular cortada do plano\(x + y + z = 1\) pelos eixos de coordenadas positivas.

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{13}{24}\)

    36. \(\vecs F(x,y,z) = 2yz\,\mathbf{\hat i} + (\tan^{-1}xz)\,\mathbf{\hat j} + e^{xy}\,\mathbf{\hat k}\)Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) onde e\(\vecs N\) é um vetor normal externo\(S,\) onde\(S\) está a superfície da esfera\(x^2 + y^2 + z^2 = 1\).

    37. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + xyz\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}\)Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) onde e\(\vecs N\) é um vetor normal externo\(S,\) onde\(S\) está\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) faltando a superfície das cinco faces do cubo unitário\(z = 0\).

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{3}{4}\)

    Para os exercícios 38 a 39, expresse a integral da superfície como uma integral dupla iterada usando uma projeção\(S\) no\(yz\) plano.

    38. \(\displaystyle \iint_S xy^2 z^3 \, dS;\)\(S\)é a primeira porção octante do plano\(2x + 3y + 4z = 12\).

    39. \(\displaystyle \iint_S (x^2 - 2y + z) \, dS;\)\(S\)é a parte do gráfico\(4x + y = 8\) limitado pelos planos e planos coordenados\(z = 6\).

    Resposta
    \(\displaystyle \int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz \, dy\)

    Para os exercícios 40 a 41, expresse a integral da superfície como uma integral dupla iterada usando uma projeção\(S\) no\(xz\) plano.

    40. \(\displaystyle \iint_S xy^2z^3 \, dS;\)\(S\)é a primeira porção octante do plano\(2x + 3y + 4z = 12\).

    41. \(\displaystyle \iint_S (x^2 - 2y + z) \, dS;\)é a parte do gráfico\(4x + y = 8\) limitado pelos planos e planos coordenados\(z = 6\).

    Resposta
    \(\displaystyle \int_0^2 \int_0^6 \big[x^2 - 2 (8 - 4x) + z\big] \sqrt{17} \, dz \, dx\)

    42. Avalie a integral da superfície\(\displaystyle \iint_S yz \, dS,\) onde\(S\) está a primeira parte octante do plano\(x + y + z = \lambda\), onde\(\lambda\) está uma constante positiva.

    43. Avalie a integral da superfície\(\displaystyle \iint_S (x^2 z + y^2 z) \, dS,\) onde\(S\) está o hemisf\(x^2 + y^2 + z^2 = a^2, \, z \geq 0.\)

    Resposta
    \(\displaystyle \iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}\)

    44. Avalie a integral da superfície\(\displaystyle \iint_S z \, dA,\) onde\(S\) está a superfície\(z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2\).

    45. Avalie a integral da superfície\(\displaystyle \iint_S x^2 yz \, dS,\) onde\(S\) está a parte do plano\(z = 1 + 2x + 3y\) que fica acima do retângulo\(0 \leq x \leq 3\)\(0 \leq y \leq 2\) e.

    Resposta
    \(\displaystyle \iint_S x^2 yz \, dS = 171 \sqrt{14}\)

    46. Avalie a integral da superfície\(\displaystyle \iint_S yz \, dS,\) onde\(S\) está o plano\(x + y + z = 1\) que está no primeiro octante.

    47. Avalie a integral da superfície\(\displaystyle \iint_S yz \, dS,\) onde\(S\) está a parte do plano\(z = y + 3\) que está dentro do cilindro\(x^2 + y^2 = 1\).

    Resposta
    \(\displaystyle \iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}\)

    Para os exercícios 48 a 50, use o raciocínio geométrico para avaliar as integrais de superfície fornecidas.

    48. \(\displaystyle \iint_S \sqrt{x^2 + y^2 + z^2} \, dS,\)onde\(S\) está a superfície\(x^2 + y^2 + z^2 = 4, \, z \geq 0\)

    49. \(\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS,\)onde\(S\) é a superfície\(x^2 + y^2 = 4, \, 1 \leq z \leq 3\), orientada com vetores unitários normais apontando para fora

    Resposta
    \(\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS = 16 \pi\)

    50. \(\displaystyle \iint_S (z\,\mathbf{\hat k}) \cdot dS,\)onde\(S\) está o disco\(x^2 + y^2 \leq 9\) no plano\(z = 4\) orientado com vetores unitários normais apontando para cima

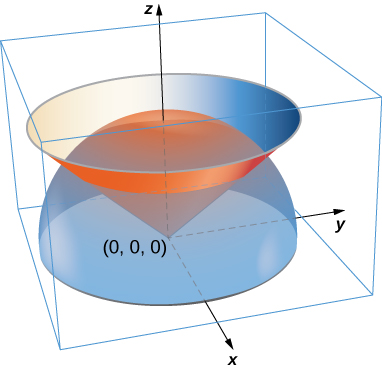
    51. Uma lâmina tem a forma de uma porção da esfera\(x^2 + y^2 + z^2 = a^2\) que fica dentro do cone\(z = \sqrt{x^2 + y^2}\). \(S\)Seja a concha esférica centrada na origem com o raio a, e\(C\) seja o cone circular direito com um vértice na origem e um eixo de simetria que\(z\) coincide com o eixo. Determine a massa da lâmina se\(\delta(x,y,z) = x^2 y^2 z\).

    Um diagrama em três dimensões. Um cone se abre para cima com um ponto na origem e uma base de simetria que coincide com o eixo z. A metade superior de um hemisfério com centro na origem se abre para baixo e é cortada pelo plano xy.

    Resposta
    \(m = \dfrac{\pi a^7}{192}\)

    52. A lamina has the shape of a portion of sphere \(x^2 + y^2 + z^2 = a^2\) that lies within cone \(z = \sqrt{x^2 + y^2}\). Let \(S\) be the spherical shell centered at the origin with radius a, and let \(C\) be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is \(\phi_0\), with \(0 \leq \phi_0 < \dfrac{\pi}{2}\). Determine the mass of that portion of the shape enclosed in the intersection of \(S\) and \(C.\) Assume \(\delta(x,y,z) = x^2y^2z.\)

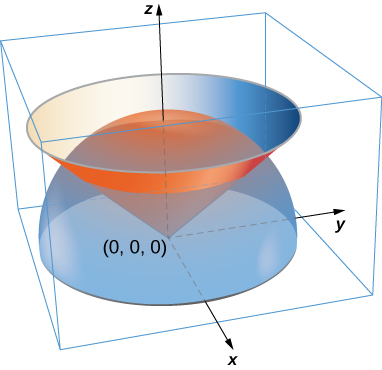
    A diagram in three dimensions. A cone opens upward with point at the origin and an asic of symmetry that coincides with the z-axis. The upper half of a hemisphere with center at the origin opens downward and is cut off by the xy-plane.

    53. Um copo de papel tem a forma de um cone circular direito invertido de altura de 6 polegadas e raio de 3 polegadas superiores. Se o copo estiver cheio de água pesando\(62.5 \, lb/ft^3\), determine a magnitude da força total exercida pela água na superfície interna do copo.

    Resposta
    \(F \approx 4.57 \, lb\)

    Para os exercícios 54 - 55, o campo vetorial de fluxo de calor para objetos condutores i\(\vecs F = - k\vecs\nabla T\), onde\(T(x,y,z)\) está a temperatura no objeto e\(k > 0\) é uma constante que depende do material. Encontre o fluxo externo\(\vecs F\) nas seguintes superfícies\(S\) para as distribuições de temperatura fornecidas e suponha\(k = 1\).

    54. \(T(x,y,z) = 100 e^{-x-y}\);\(S\) consiste nas faces do cubo\(|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1\).

    55. \(T(x,y,z) = - \ln (x^2 + y^2 + z^2)\);\(S\) é esfera\(x^2 + y^2 + z^2 = a^2\).

    Resposta
    \(8\pi a\)

    Para os exercícios 56 a 57, considere os campos radiais\(\vecs F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{\dfrac{p}{2}}} = \dfrac{r}{|r|^p}\), onde\(p\) está um número real. Vamos\(S\) consistir em esferas\(A\) e\(B\) centradas na origem com raios\(0 < a < b\). O fluxo externo total\(S\) consiste no fluxo externo através da esfera externa,\(B\) menos o fluxo para dentro\(S\) da esfera interna.\(A.\)

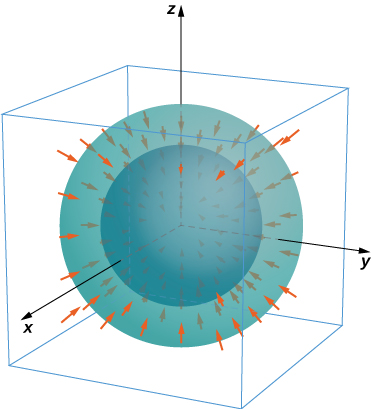
    Um diagrama em três dimensões de duas esferas, uma contida completamente dentro da outra. Seus centros estão ambos na origem. As setas apontam para a origem de fora de ambas as esferas.

    56. Encontre o fluxo total entre

    Template:ContribOpenStaxCalc