16.6: Integrais de superfície
- Page ID
- 188468
- Encontre as representações paramétricas de um cilindro, um cone e uma esfera.
- Descreva a integral da superfície de uma função de valor escalar sobre uma superfície paramétrica.
- Use uma integral de superfície para calcular a área de uma determinada superfície.
- Explique o significado de uma superfície orientada, dando um exemplo.
- Descreva a integral da superfície de um campo vetorial.
- Use integrais de superfície para resolver problemas aplicados.
Vimos que uma integral de linha é uma integral sobre um caminho em um plano ou no espaço. No entanto, se quisermos nos integrar sobre uma superfície (um objeto bidimensional) em vez de um caminho (um objeto unidimensional) no espaço, precisamos de um novo tipo de integral que possa lidar com a integração de objetos em dimensões mais altas. Podemos estender o conceito de uma integral de linha para uma integral de superfície para nos permitir realizar essa integração.
Integrais de superfície são importantes pelos mesmos motivos que integrais de linha. Eles têm muitas aplicações em física e engenharia e nos permitem desenvolver versões de maior dimensão do Teorema Fundamental do Cálculo. Em particular, integrais de superfície nos permitem generalizar o teorema de Green para dimensões mais altas, e elas aparecem em alguns teoremas importantes que discutimos em seções posteriores.
Superfícies paramétricas
Uma integral de superfície é semelhante a uma integral de linha, exceto que a integração é feita sobre uma superfície em vez de um caminho. Nesse sentido, integrais de superfície expandem nosso estudo de integrais de linha. Assim como com integrais de linha, existem dois tipos de integrais de superfície: uma integral de superfície de uma função de valor escalar e uma integral de superfície de um campo vetorial.
No entanto, antes de podermos nos integrar sobre uma superfície, precisamos considerar a superfície em si. Lembre-se de que, para calcular uma integral de linha escalar ou vetorial sobre a curva\(C\), primeiro precisamos parametrizar\(C\). De forma semelhante, para calcular uma superfície integral sobre a superfície\(S\), precisamos parametrizar\(S\). Ou seja, precisamos de um conceito funcional de uma superfície parametrizada (ou superfície paramétrica), da mesma forma que já temos um conceito de curva parametrizada.
Uma superfície parametrizada é dada por uma descrição do formulário
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
Observe que essa parametrização envolve dois parâmetros\(u\) e\(v\), como uma superfície é bidimensional, são necessárias duas variáveis para traçar a superfície. Os parâmetros\(u\)\(v\) variam em uma região chamada domínio do parâmetro, ou espaço de parâmetros — o conjunto de pontos no\(uv\) plano -que podem ser substituídos\(\vecs r\). Cada opção de\(u\) e\(v\) no domínio do parâmetro fornece um ponto na superfície, assim como cada escolha de um parâmetro\(t\) fornece um ponto em uma curva parametrizada. Toda a superfície é criada fazendo todas as escolhas possíveis de\(u\) e\(v\) sobre o domínio do parâmetro.
Dada uma parametrização da superfície
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
o domínio do parâmetro da parametrização é o conjunto de pontos no\(uv\) plano -que podem ser substituídos\(\vecs r\).
Descreva superfície\(S\) parametrizada por
\[\vecs{r}(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, -\infty < u < \infty, \, -\infty < v < \infty. \nonumber \]
Solução
Para ter uma ideia da forma da superfície, primeiro traçamos alguns pontos. Como o domínio do parâmetro é tudo\(\mathbb{R}^2\), podemos escolher qualquer valor para u e v e traçar o ponto correspondente. Se\(u = v = 0\), então\(\vecs r(0,0) = \langle 1,0,0 \rangle\), o ponto (1, 0, 0) estiver ativado\(S\). Da mesma forma, aponta\(\vecs r(\pi, 2) = (-1,0,2)\) e\(\vecs r \left(\dfrac{\pi}{2}, 4\right) = (0,1,4)\) está ligado\(S\).
Embora os pontos de plotagem possam nos dar uma ideia da forma da superfície, geralmente precisamos de alguns pontos para ver a forma. Como é demorado traçar dezenas ou centenas de pontos, usamos outra estratégia. Para visualizar\(S\), visualizamos duas famílias de curvas que se encontram\(S\). Na primeira família de curvas, mantemos\(u\) constantes; na segunda família de curvas, mantemos\(v\) constantes. Isso nos permite construir um “esqueleto” da superfície, tendo assim uma ideia de sua forma.
- Suponha que\(u\) seja uma constante\(K\). Então, a curva traçada pela parametrização é\(\langle \cos K, \, \sin K, \, v \rangle \), que fornece uma linha vertical que passa pelo ponto\((\cos K, \sin K, v \rangle\) no\(xy\) plano.
- Suponha que\(v\) seja uma constante\(K\). Então, a curva traçada pela parametrização é\(\langle \cos u, \, \sin u, \, K \rangle \), que dá um círculo no plano\(z = K\) com raio 1 e centro\((0, 0, K)\).
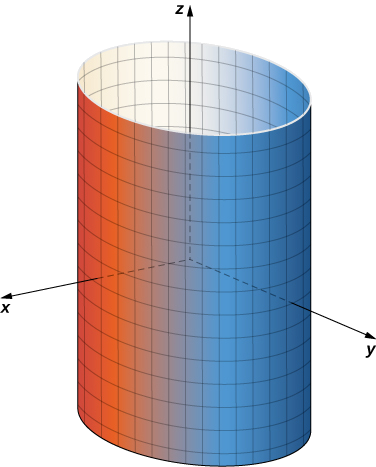
Se\(u\) for mantido constante, obtemos linhas verticais; se\(v\) for mantido constante, obtemos círculos de raio 1 centrados em torno da linha vertical que passa pela origem. Portanto, a superfície traçada pela parametrização é cilíndrica\(x^2 + y^2 = 1\) (Figura\(\PageIndex{1}\)).
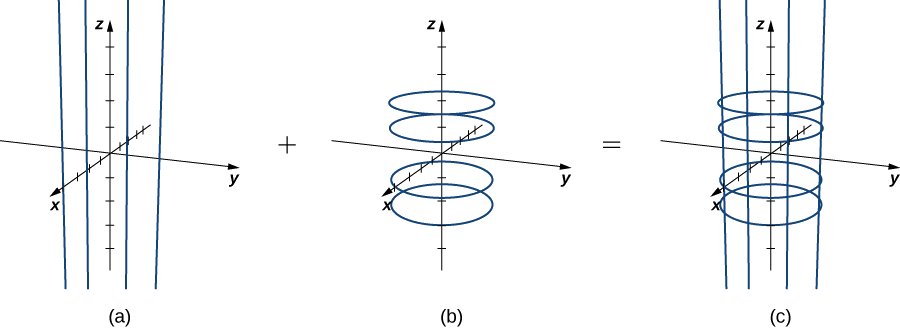
Observe que se\(x = \cos u\) e\(y = \sin u\), então\(x^2 + y^2 = 1\), os pontos de S realmente estão no cilindro. Por outro lado, cada ponto do cilindro está contido em algum círculo\(\langle \cos u, \, \sin u, \, k \rangle \) para alguns e\(k\), portanto, cada ponto no cilindro está contido na superfície parametrizada (Figura\(\PageIndex{2}\)).
Análise
Observe que, se mudarmos o domínio do parâmetro, poderemos obter uma superfície diferente. Por exemplo, se restringirmos o domínio a\(0 \leq u \leq \pi, \, -\infty < v < 6\), a superfície seria um meio cilindro de altura 6.
Descreva a superfície com parametrização
\[\vecs{r} (u,v) = \langle 2 \, \cos u, \, 2 \, \sin u, \, v \rangle, \, 0 \leq u \leq 2\pi, \, -\infty < v < \infty \nonumber \]
- Dica
-
Mantenha a posição\(v\) constante\(u\) e veja que tipo de curvas resultam.
- Responda
-
cilindro\(x^2 + y^2 = 4\)
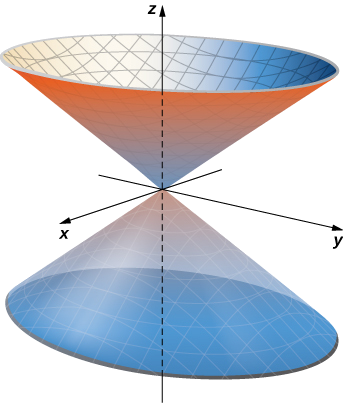
Dê uma parametrização do cone que\(x^2 + y^2 = z^2\) está sobre ou acima do plano\(z = -2\).
Solução
A seção transversal horizontal do cone em altura\(z = u\) é circular\(x^2 + y^2 = u^2\). Portanto, um ponto no cone em altura\(u\) tem coordenadas\((u \, \cos v, \, u \, \sin v, \, u)\) para o ângulo\(v\). Portanto, uma parametrização do cone é\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle \). Como não estamos interessados em todo o cone, somente na parte no plano ou acima dele\(z = -2\), o domínio do parâmetro é dado por\(-2 < u < \infty, \, 0 \leq v < 2\pi\) (Figura\(\PageIndex{4}\)).
Dê uma parametrização para a porção do cone\(x^2 + y^2 = z^2\) que está no primeiro octante.
- Dica
-
Considere o domínio do parâmetro para essa superfície.
- Responda
-
\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 < u < \infty, \, 0 \leq v < \dfrac{\pi}{2}\)
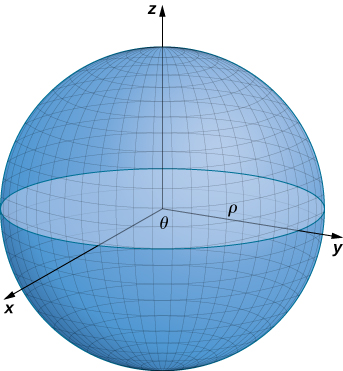
Discutimos as parametrizações de várias superfícies, mas dois tipos importantes de superfícies precisam de uma discussão separada: esferas e gráficos de funções com duas variáveis. Para parametrizar uma esfera, é mais fácil usar coordenadas esféricas. A esfera de raio\(\rho\) centrada na origem é dada pela parametrização
\(\vecs r(\phi,\theta) = \langle \rho \, \cos \theta \, \sin \phi, \, \rho \, \sin \theta \, \sin \phi, \, \rho \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi.\)
A ideia dessa parametrização é que,\(\phi\) à medida que avança para baixo a partir do\(z\) eixo positivo, um círculo de raio\(\rho \, \sin \phi\) é traçado deixando\(\theta\) correr de 0 para\(2\pi\). Para ver isso, vamos\(\phi\) consertar. Então
\ [\ begin {align*} x^2 + y^2 &= (\ rho\,\ cos\ theta\,\ sin\ phi) ^2 + (\ rho\,\ sin\ theta\,\ sin\ phi) ^2\\ [4pt]
&=\ rho^2\ sin^2\ phi (\ cos^2\ theta +\ sin^2\ theta)\\ [4pt]
&=\ rho^2\,\ sin^2\ phi\\ [4pt]
&= (\ rho\,\ sin\ phi) ^2. \ end {align*}\]
Isso resulta no círculo desejado (Figura\(\PageIndex{5}\)).
Finalmente, para parametrizar o gráfico de uma função de duas variáveis, primeiro deixamos\(z = f(x,y)\) ser uma função de duas variáveis. A parametrização mais simples do gráfico de\(f\) é\(\vecs r(x,y) = \langle x,y,f(x,y) \rangle\), onde\(x\) e\(y\) varia sobre o domínio de\(f\) (Figura\(\PageIndex{6}\)). Por exemplo, o gráfico de\(f(x,y) = x^2 y\) pode ser parametrizado por\(\vecs r(x,y) = \langle x,y,x^2y \rangle\), onde\(x\) os parâmetros\(y\) variam no domínio de\(f\). Se nos importarmos apenas com uma parte do gráfico\(f\) - digamos, a parte do gráfico sobre o retângulo\([ 1,3] \times [2,5]\) - então podemos restringir o domínio do parâmetro para dar essa parte da superfície:
\[\vecs r(x,y) = \langle x,y,x^2y \rangle, \, 1 \leq x \leq 3, \, 2 \leq y \leq 5. \nonumber \]
Da mesma forma, se\(S\) for uma superfície dada por equação\(x = g(y,z)\) ou equação\(y = h(x,z)\), então uma parametrização de\(S\) é\(\vecs r(y,z) = \langle g(y,z), \, y,z\rangle\) ou\(\vecs r(x,z) = \langle x,h(x,z), z\rangle\), respectivamente. Por exemplo, o gráfico do parabolóide\(2y = x^2 + z^2\) pode ser parametrizado por\(\vecs r(x,y) = \left\langle x, \dfrac{x^2+z^2}{2}, z \right\rangle, \, 0 \leq x < \infty, \, 0 \leq z < \infty\). Observe que não precisamos variar em todo o domínio de\(y\) porque\(x\) e\(z\) estamos ao quadrado.
Vamos agora generalizar as noções de suavidade e regularidade para uma superfície paramétrica. Lembre-se de que a parametrização da curva\(\vecs r(t), \, a \leq t \leq b\) é regular (ou suave), se for\(\vecs r'(t) \neq \vecs 0\) para todos\(t\)\([a,b]\). Para uma curva, essa condição garante que a imagem de\(\vecs r\) realmente seja uma curva, e não apenas um ponto. Por exemplo, considere a parametrização de curvas\(\vecs r(t) = \langle 1,2\rangle, \, 0 \leq t \leq 5\). A imagem dessa parametrização é simplesmente um ponto\((1,2)\), que não é uma curva. Observe também que\(\vecs r'(t) = \vecs 0\). O fato de a derivada ser o vetor zero indica que não estamos realmente olhando para uma curva.
Analogamente, gostaríamos de ter uma noção de regularidade (ou suavidade) para superfícies para que uma parametrização de superfície realmente trace uma superfície. Para motivar a definição da regularidade de uma parametrização de superfície, considere a parametrização
\[\vecs r(u,v) = \langle 0, \, \cos v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq \pi. \nonumber \]
Embora essa parametrização pareça ser a parametrização de uma superfície, observe que a imagem é na verdade uma linha (Figura\(\PageIndex{7}\)). Como podemos evitar parametrizações como essa? Parametrizações que não fornecem uma superfície real? Observe que\(\vecs r_u = \langle 0,0,0 \rangle\) e\(\vecs r_v = \langle 0, -\sin v, 0\rangle\), e o produto cruzado correspondente é zero. O análogo da condição\(\vecs r'(t) = \vecs 0\) é que não\(\vecs r_u \times \vecs r_v\) é zero para o ponto\((u,v)\) no domínio do parâmetro, que é uma parametrização regular.
A parametrização\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) é uma parametrização regular se não\(\vecs r_u \times \vecs r_v\) for zero para o ponto\((u,v)\) no domínio do parâmetro.
Se a parametrização\(\vec{r}\) for regular, a imagem de\(\vec{r}\) é um objeto bidimensional, como uma superfície deveria ser. Ao longo deste capítulo, as parametrizações\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) são consideradas regulares.
Lembre-se de que a parametrização da curva\(\vecs r(t), \, a \leq t \leq b\)\(\vecs r'(t)\) é suave se for contínua e\(\vecs r'(t) \neq \vecs 0\) para todos\(t\) em\([a,b]\). Informalmente, a parametrização da curva é suave se a curva resultante não tiver cantos nítidos. A definição de uma parametrização de superfície lisa é similar. Informalmente, a parametrização da superfície é suave se a superfície resultante não tiver cantos afiados.
A parametrização da superfície\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) é suave se o vetor\(\vecs r_u \times \vecs r_v\) não for zero para qualquer opção de\(u\) e\(v\) no domínio do parâmetro.
Uma superfície também pode ser lisa por partes se tiver faces lisas, mas também tiver locais onde as derivadas direcionais não existem.
Qual das figuras na Figura\(\PageIndex{8}\) é lisa?

Solução
A superfície na Figura\(\PageIndex{8a}\) pode ser parametrizada por
\[\vecs r(u,v) = \langle (2 + \cos v) \cos u, \, (2 + \cos v) \sin u, \, \sin v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v < 2\pi \nonumber \]
(podemos usar a tecnologia para verificar). Observe que os vetores
\[\vecs r_u = \langle - (2 + \cos v)\sin u, \, (2 + \cos v) \cos u, 0 \rangle \nonumber \]
e
\[\vecs r_v = \langle -\sin v \, \cos u, \, - \sin v \, \sin u, \, \cos v \rangle \nonumber \]
existe para qualquer opção de\(u\) e\(v\) no domínio do parâmetro, e
\[ \begin{align*} \vecs r_u \times \vecs r_v &= \begin{vmatrix} \mathbf{\hat{i}}& \mathbf{\hat{j}}& \mathbf{\hat{k}} \\ -(2 + \cos v)\sin u & (2 + \cos v)\cos u & 0\\ -\sin v \, \cos u & - \sin v \, \sin u & \cos v \end{vmatrix} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [2 + \cos v) \sin u \, \cos v] \mathbf{\hat{j}} + [(2 + \cos v)\sin v \, \sin^2 u + (2 + \cos v) \sin v \, \cos^2 u]\mathbf{\hat{k}} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [(2 + \cos v) \sin u \, \cos v]\mathbf{\hat{j}} + [(2 + \cos v)\sin v ] \mathbf{\hat{k}}. \end{align*}\]
O\(\mathbf{\hat{k}}\) componente desse vetor é zero somente se\(v = 0\) ou\(v = \pi\). Se\(v = 0\) ou\(v = \pi\), então as únicas opções para\(u\) que o\(\mathbf{\hat{j}}\) componente seja zero são\(u = 0\) ou\(u = \pi\). Porém, essas escolhas de\(u\) não tornam o\(\mathbf{\hat{i}}\) componente zero. Portanto, não\(\vecs r_u \times \vecs r_v\) é zero para qualquer opção de\(u\) e\(v\) no domínio do parâmetro, e a parametrização é suave. Observe que a superfície correspondente não tem cantos afiados.
Na pirâmide da Figura\(\PageIndex{8b}\), a nitidez dos cantos garante que não existam derivadas direcionais nesses locais. Portanto, a pirâmide não tem uma parametrização suave. No entanto, a pirâmide consiste em quatro faces lisas e, portanto, essa superfície é lisa por partes.
A parametrização da superfície é\(\vecs r(u,v) = \langle u^{2v}, v + 1, \, \sin u \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3\) suave?
- Dica
-
Investigue o produto cruzado\(\vecs r_u \times \vecs r_v\).
- Responda
-
sim
Área de superfície de uma superfície paramétrica
Nosso objetivo é definir uma integral de superfície e, como primeira etapa, examinamos como parametrizar uma superfície. A segunda etapa é definir a área da superfície de uma superfície paramétrica. A notação necessária para desenvolver essa definição é usada no restante deste capítulo.
\(S\)Seja uma superfície com parametrização\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) sobre algum domínio de parâmetros\(D\). Assumimos aqui e por toda parte que a parametrização da superfície\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) é continuamente diferenciável, ou seja, cada função componente tem derivadas parciais contínuas. Suponha, por uma questão de simplicidade, que\(D\) seja um retângulo (embora o material a seguir possa ser estendido para lidar com domínios de parâmetros não retangulares). Divida o retângulo\(D\) em sub-retângulos\(D_{ij}\) com largura horizontal\(\Delta u\) e comprimento vertical\(\Delta v\). Suponha que i varie de 1 a m e j varie de 1 a n, de modo que\(D\) seja subdividido em mn retângulos. Essa divisão de\(D\) em sub-retângulos fornece uma divisão correspondente da superfície\(S\) em pedaços\(S_{ij}\). Escolha um ponto\(P_{ij}\) em cada peça\(S_{ij}\). O ponto\(P_{ij}\) corresponde ao ponto\((u_i, v_j)\) no domínio do parâmetro.
Observe que podemos formar uma grade com linhas paralelas ao\(u\) eixo -e ao\(v\) eixo\(uv\) -no plano. Essas linhas de grade correspondem a um conjunto de curvas de grade na superfície\(S\) que é parametrizado por\(\vecs r(u,v)\). Sem perda de generalidade, assumimos que\(P_{ij}\) está localizado no canto de duas curvas de grade, como na Figura\(\PageIndex{9}\). Se pensarmos em um mapeamento do\(uv\) plano -para\(\mathbb{R}^3\), as curvas da grade são a imagem das linhas da grade abaixo\(\vecs r\).\(\vecs r\) Para ser preciso, considere as linhas da grade que passam pelo ponto\((u_i, v_j)\). Uma linha é dada por\(x = u_i, \, y = v\); a outra é dada por\(x = u, \, y = v_j\). Na primeira linha da grade, o componente horizontal é mantido constante, produzindo uma linha vertical\((u_i, v_j)\). Na segunda linha da grade, o componente vertical é mantido constante, produzindo uma linha horizontal\((u_i, v_j)\). As curvas de grade correspondentes são\(\vecs r(u_i, v)\)\((u, v_j)\) e e essas curvas se cruzam no ponto\(P_{ij}\).
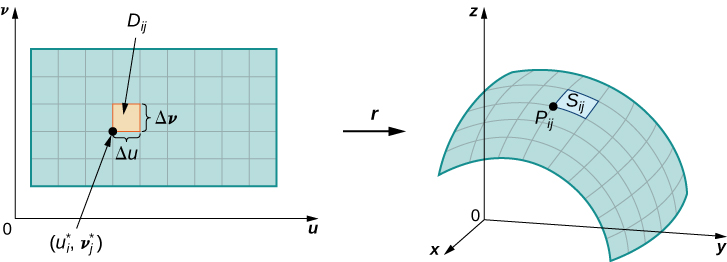
Agora, considere os vetores que são tangentes a essas curvas de grade. Para curva de grade\(\vecs r(u_i,v)\), o vetor tangente em\(P_{ij}\) é
\[\vecs t_v (P_{ij}) = \vecs r_v (u_i,v_j) = \langle x_v (u_i,v_j), \, y_v(u_i,v_j), \, z_v (u_i,v_j) \rangle. \nonumber \]
Para curva de grade\(\vecs r(u, v_j)\), o vetor tangente em\(P_{ij}\) é
\[\vecs t_u (P_{ij}) = \vecs r_u (u_i,v_j) = \langle x_u (u_i,v_j), \, y_u(u_i,v_j), \, z_u (u_i,v_j) \rangle. \nonumber \]
Se o vetor\(\vecs N = \vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})\) existe e não é zero, então o plano tangente em\(P_{ij}\) existe (Figura\(\PageIndex{10}\)). Se a peça\(S_{ij}\) for pequena o suficiente, então o plano tangente no ponto\(P_{ij}\) é uma boa aproximação da peça\(S_{ij}\).
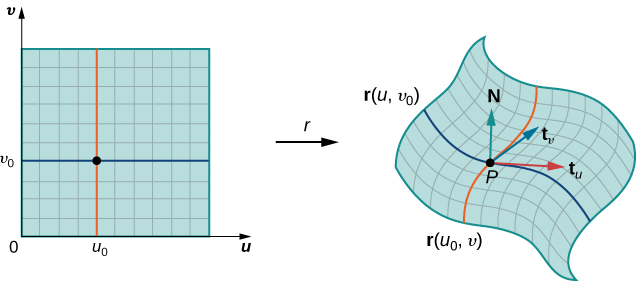
O plano tangente em\(P_{ij}\) contém vetores\(\vecs t_u(P_{ij})\)\(\vecs t_v(P_{ij})\) e, portanto, o paralelogramo abrangido por\(\vecs t_u(P_{ij})\) e\(\vecs t_v(P_{ij})\) está no plano tangente. Como o retângulo original no\(uv\) plano -correspondente a\(S_{ij}\) tem largura\(\Delta u\) e comprimento\(\Delta v\), o paralelogramo que usamos para aproximar\(S_{ij}\) é o paralelogramo abrangido por\(\Delta u \vecs t_u(P_{ij})\)\(\Delta v \vecs t_v(P_{ij})\) e. Em outras palavras, escalamos os vetores tangentes pelas constantes\(\Delta u\) e\(\Delta v\) para corresponder à escala da divisão original dos retângulos no domínio do parâmetro. Portanto, a área do paralelogramo usada para aproximar a área de\(S_{ij}\) é
\[\Delta S_{ij} \approx ||(\Delta u \vecs t_u (P_{ij})) \times (\Delta v \vecs t_v (P_{ij})) || = ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij}) || \Delta u \,\Delta v. \nonumber \]
O ponto variável\(P_{ij}\) sobre todas as peças\(S_{ij}\) e a aproximação anterior levam à seguinte definição da área de superfície de uma superfície paramétrica (Figura\(\PageIndex{11}\)).
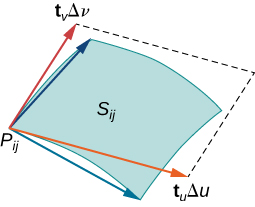
\(D\)Seja\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) com o domínio do parâmetro uma parametrização suave da superfície\(S\). Além disso, suponha que\(S\) seja rastreado apenas uma vez, pois\((u,v)\) varia\(D\). A área da superfície de\(S\) é
\[\iint_D ||\vecs t_u \times \vecs t_v || \,dA, \label{equation1} \]
onde\(\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\)
e
\[\vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
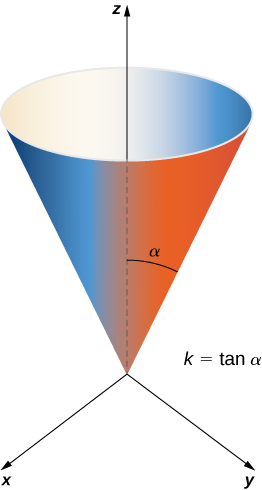
Calcule a área da superfície lateral (a área do “lado”, sem incluir a base) do cone circular direito com altura h e raio r.
Solução
Antes de calcular a área da superfície desse cone usando a Equação\ ref {equation1}, precisamos de uma parametrização. Assumimos que esse cone está\(\mathbb{R}^3\) com seu vértice na origem (Figura\(\PageIndex{12}\)). Para obter uma parametrização,\(\alpha\) seja o ângulo que é varrido começando no eixo z positivo e terminando no cone, e deixe\(k = \tan \alpha\). Para um valor de altura\(v\) com\(0 \leq v \leq h\), o raio do círculo formado pela interseção do cone com o plano\(z = v\) é\(kv\). Portanto, uma parametrização desse cone é
\[\vecs s(u,v) = \langle kv \, \cos u, \, kv \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h. \nonumber \]
A ideia por trás dessa parametrização é que, para um\(v\) valor fixo, o círculo varrido deixando\(u\) variar é o círculo em altura\(v\) e raio\(kv\). À medida que\(v\) aumenta, a parametrização varre uma “pilha” de círculos, resultando no cone desejado.
Com uma parametrização em mãos, podemos calcular a área da superfície do cone usando a Equação\ ref {equation1}. Os vetores tangentes são\(\vecs t_u = \langle - kv \, \sin u, \, kv \, \cos u, \, 0 \rangle\)\(\vecs t_v = \langle k \, \cos u, \, k \, \sin u, \, 1 \rangle\) e. Portanto,
\[ \begin{align*} \vecs t_u \times \vecs t_v &= \begin{vmatrix} \mathbf{\hat{i}} & \mathbf{\hat{j}} & \mathbf{\hat{k}} \\ -kv \sin u & kv \cos u & 0 \\ k \cos u & k \sin u & 1 \end{vmatrix} \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \, \sin^2 u - k^2 v \, \cos^2 u \rangle \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, - k^2 v \rangle. \end{align*}\]
A magnitude desse vetor é
\[ \begin{align*} ||\langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \rangle || &= \sqrt{k^2 v^2 \cos^2 u + k^2 v^2 \sin^2 u + k^4v^2} \\[4pt] &= \sqrt{k^2v^2 + k^4v^2} \\[4pt] &= kv\sqrt{1 + k^2}. \end{align*}\]
Pela Equação\ ref {equation1}, a área da superfície do cone é
\[ \begin{align*}\iint_D ||\vecs t_u \times \vecs t_v|| \, dA &= \int_0^h \int_0^{2\pi} kv \sqrt{1 + k^2} \,du\, dv \\[4pt] &= 2\pi k \sqrt{1 + k^2} \int_0^h v \,dv \\[4pt] &= 2 \pi k \sqrt{1 + k^2} \left[\dfrac{v^2}{2}\right]_0^h \\[4pt] \\[4pt] &= \pi k h^2 \sqrt{1 + k^2}. \end{align*}\]
Uma vez que\(k = \tan \alpha = r/h\),
\[ \begin{align*} \pi k h^2 \sqrt{1 + k^2} &= \pi \dfrac{r}{h}h^2 \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] &= \pi r h \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] \\[4pt] &= \pi r \sqrt{h^2 + h^2 \left(\dfrac{r^2}{h^2}\right) } \\[4pt] &= \pi r \sqrt{h^2 + r^2}. \end{align*}\]
Portanto, a área da superfície lateral do cone é\(\pi r \sqrt{h^2 + r^2}\).
AnáliseA área da superfície de um cone circular reto com raio\(r\) e altura geralmente\(h\) é dada como\(\pi r^2 + \pi r \sqrt{h^2 + r^2}\). A razão para isso é que a base circular é incluída como parte do cone e, portanto, a área da base\(\pi r^2\) é adicionada à área da superfície lateral\(\pi r \sqrt{h^2 + r^2}\) que encontramos.
Encontre a área da superfície com parametrização\(\vecs r(u,v) = \langle u + v, \, u^2, \, 2v \rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 2\).
- Dica
-
Use a Equação\ ref {equation1}.
- Responda
-
\(\≈ 43.02\)
Mostre que a área da superfície da esfera\(x^2 + y^2 + z^2 = r^2\) é\(4 \pi r^2\).
Solução
A esfera tem parametrização
\(r \, \cos \theta \, \sin \phi, \, r \, \sin \theta \, \sin \phi, \, r \, \cos \phi \rangle, \, 0 \leq \theta < 2\pi, \, 0 \leq \phi \leq \pi.\)
Os vetores tangentes são
\(\vecs t_{\theta} = \langle -r \, \sin \theta \, \sin \phi, \, r \, \cos \theta \, \sin \phi, \, 0 \rangle\)
e
\(\vecs t_{\phi} = \langle r \, \cos \theta \, \cos \phi, \, r \, \sin \theta \, \cos \phi, \, -r \, \sin \phi \rangle.\)
Portanto,
\[ \begin{align*}\vecs t_{\phi} \times \vecs t_{\theta} &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin^2 \theta \, \sin \phi \, \cos \phi + r^2 \cos^2 \theta \, \sin \phi \, \cos \phi \rangle \\[4pt] &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin \phi \, \cos \phi \rangle. \end{align*}\]
Agora,
\[ \begin{align*}||\vecs t_{\phi} \times \vecs t_{\theta} || &= \sqrt{r^4\sin^4\phi \, \cos^2 \theta + r^4 \sin^4 \phi \, \sin^2 \theta + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= \sqrt{r^4 \sin^4 \phi + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= r^2 \sqrt{\sin^2 \phi} \\[4pt] &= r \, \sin \phi.\end{align*}\]
Observe isso\(\sin \phi \geq 0\) no domínio do parâmetro porque\(0 \leq \phi < \pi\), e isso justifica a equação\(\sqrt{\sin^2 \phi} = \sin \phi\). A área da superfície da esfera é
\[\int_0^{2\pi} \int_0^{\pi} r^2 \sin \phi \, d\phi \,d\theta = r^2 \int_0^{2\pi} 2 \, d\theta = 4\pi r^2. \nonumber \]
Derivamos a fórmula familiar para a área de superfície de uma esfera usando integrais de superfície.
Mostre que a área da superfície do cilindro\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\) é\(2\pi rh\). Observe que esse cilindro não inclui os círculos superior e inferior.
- Dica
-
Use a parametrização padrão de um cilindro e siga o exemplo anterior.
- Responda
-
Com a parametrização padrão de um cilindro, a Equação\ ref {equation1} mostra que a área da superfície é\(2 \pi rh\).
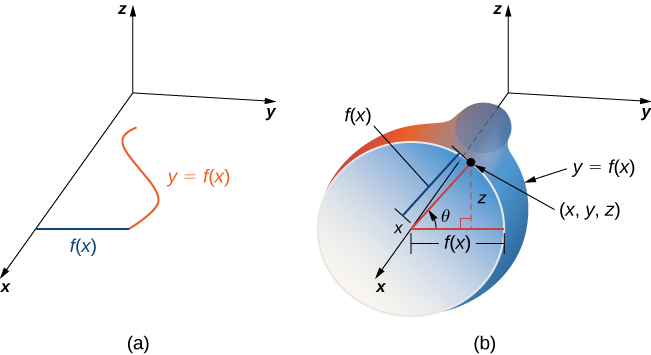
Além de parametrizar superfícies dadas por equações ou formas geométricas padrão, como cones e esferas, também podemos parametrizar superfícies de revolução. Portanto, podemos calcular a área da superfície de uma superfície de revolução usando as mesmas técnicas. \(y = f(x) \geq 0\)Seja uma função positiva de variável única no domínio\(a \leq x \leq b\) e\(S\) seja a superfície obtida girando em\(f\) torno do\(x\) eixo -( Figura\(\PageIndex{13}\)). \(\theta\)Seja o ângulo de rotação. Em seguida,\(S\) pode ser parametrizado com parâmetros\(x\) e\(\theta\) por
\[\vecs r(x, \theta) = \langle x, f(x) \, \cos \theta, \, f(x) \sin \theta \rangle, \, a \leq x \leq b, \, 0 \leq x \leq 2\pi. \nonumber \]
Encontre a área da superfície de revolução obtida girando em\(y = x^2, \, 0 \leq x \leq b\) torno do eixo x (Figura\(\PageIndex{14}\)).
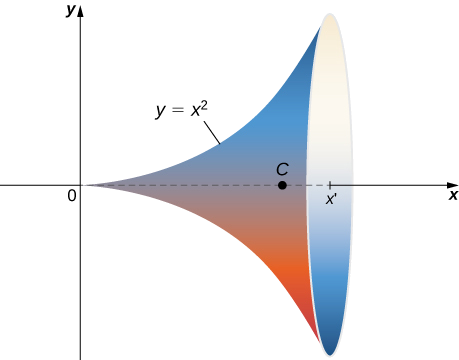
Solução
Esta superfície tem parametrização\(\vecs r(x, \theta) = \langle x, \, x^2 \cos \theta, \, x^2 \sin \theta \rangle, \, 0 \leq x \leq b, \, 0 \leq x < 2\pi.\)
Os vetores tangentes são\( \vecs t_x = \langle 1, \, 2x \, \cos \theta, \, 2x \, \sin \theta \rangle\)\(\vecs t_{\theta} = \langle 0, \, -x^2 \sin \theta, \, -x^2 \cos \theta \rangle\) e.
Portanto,
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \langle 2x^3 \cos^2 \theta + 2x^3 \sin^2 \theta, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \\[4pt] &= \langle 2x^3, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \end{align*}\]
e
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \sqrt{4x^6 + x^4\cos^2 \theta + x^4 \sin^2 \theta} \\[4pt] &= \sqrt{4x^6 + x^4} \\[4pt] &= x^2 \sqrt{4x^2 + 1} \end{align*}\]
A área da superfície da revolução é
\ [\ begin {align*}\ int_0^b\ int_0^ {2\ pi} x^2\ sqrt {4x^2 + 1}\, d\ theta\, dx &= 2\ pi\ int_0^b x^2\ sqrt {4x^2 + 1}\, dx\\ [4pt]
&= 2\ pi\ left [\ dfrac {1} {64}\ esquerda (2\ sqrt {4x^2 + 1} (8x^3 + x)\,\ sinh^ {-1} (2x)\ direita)\ direita] _0^b\\ [4pt]
&= 2\ pi\ left [\ dfrac {1} {64}\ left (2 \ sqrt {4b^2 + 1} (8b^3 + b)\,\ sinh^ {-1} (2b)\ direita)\ direita]. \ end {align*}\]
Use a Equação\ ref {equation1} para encontrar a área da superfície de revolução obtida pela curva de rotação em\(y = \sin x, \, 0 \leq x \leq \pi\) torno do\(x\) eixo.
- Dica
-
Use a parametrização das superfícies de revolução fornecida antes do Exemplo\(\PageIndex{7}\).
- Responda
-
\(2\pi (\sqrt{2} + \sinh^{-1} (1))\)
Integral de superfície de uma função de valor escalar
Agora que podemos parametrizar superfícies e calcular suas áreas de superfície, podemos definir integrais de superfície. Primeiro, vamos examinar a integral da superfície de uma função de valor escalar. Informalmente, a integral de superfície de uma função de valor escalar é um análogo de uma integral de linha escalar em uma dimensão superior. O domínio de integração de uma integral de linha escalar é uma curva parametrizada (um objeto unidimensional); o domínio de integração de uma integral de superfície escalar é uma superfície parametrizada (um objeto bidimensional). Portanto, a definição de uma integral de superfície segue bem de perto a definição de uma integral de linha. Para integrais de linha escalar, cortamos a curva do domínio em pequenos pedaços, escolhemos um ponto em cada peça, calculamos a função nesse ponto e calculamos o limite da soma de Riemann correspondente. Para integrais de superfície escalar, cortamos a região do domínio (não mais uma curva) em pequenos pedaços e procedemos da mesma forma.
\(S\)Seja uma superfície lisa por partes com parametrização\(\vecs{r}(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle \) com domínio de parâmetros\(D\) e\(f(x,y,z)\) seja uma função com um domínio que contém\(S\). Por enquanto, suponha que o domínio do parâmetro\(D\) seja um retângulo, mas podemos estender a lógica básica de como procedemos para qualquer domínio de parâmetros (a escolha de um retângulo é simplesmente tornar a notação mais gerenciável). Divida o retângulo\(D\) em sub-retângulos\(D_{ij}\) com largura horizontal\(\Delta u\) e comprimento vertical\(\Delta v\). Suponha que\(i\) varie de\(1\) até\(m\) e\(j\) varie de\(1\) até\(n\), de modo que\(D\) seja subdividido em\(mn\) retângulos. Essa divisão de\(D\) em subretângulos fornece uma divisão correspondente de\(S\) em pedaços\(S_{ij}\). Escolha um ponto\(P_{ij}\) em cada peça\(f\),\(S_{ij}\) avalie\(P_{ij}\) em e multiplique por área\(S_{ij}\) para formar a soma de Riemann.
\[\sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \, \Delta S_{ij}. \nonumber \]
Para definir uma integral de superfície de uma função de valor escalar, deixamos as áreas das peças\(S\) encolherem para zero tomando um limite.
A integral da superfície de uma função de valor escalar de\(f\) sobre uma superfície lisa por partes\(S\) é
\[\iint_S f(x,y,z) dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}. \nonumber \]
Novamente, observe as semelhanças entre essa definição e a definição de uma integral de linha escalar. Na definição de uma integral de linha, cortamos uma curva em pedaços, calculamos uma função em um ponto em cada peça e deixamos o comprimento das peças encolher até zero, tomando o limite da soma de Riemann correspondente. Na definição de uma integral de superfície, cortamos uma superfície em pedaços, avaliamos uma função em um ponto de cada peça e deixamos a área das peças encolher até zero, tomando o limite da soma de Riemann correspondente. Assim, uma integral de superfície é semelhante a uma integral de linha, mas em uma dimensão superior.
A definição de uma integral de linha escalar pode ser estendida para domínios de parâmetros que não são retângulos usando a mesma lógica usada anteriormente. A ideia básica é dividir o domínio do parâmetro em pequenos pedaços, escolher um ponto de amostra em cada peça e assim por diante. A forma exata de cada peça no domínio da amostra se torna irrelevante à medida que as áreas das peças diminuem para zero.
Integrais de superfície escalar são difíceis de calcular a partir da definição, assim como integrais de linha escalar. Para desenvolver um método que torne as integrais de superfície mais fáceis de calcular, aproximamos as áreas da superfície\(\Delta S_{ij}\) com pequenos pedaços de um plano tangente, assim como fizemos na subseção anterior. Lembre-se da definição de vetores\(\vecs t_u\) e\(\vecs t_v\):
\[\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\, \text{and} \, \vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Pelo material que já estudamos, sabemos que
\[\Delta S_{ij} \approx ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})|| \,\Delta u \,\Delta v. \nonumber \]
Portanto,
\[\iint_S f(x,y,z) \,dS \approx \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij})|| \vecs t_u(P_{ij}) \times \vecs t_v(P_{ij}) ||\,\Delta u \,\Delta v. \nonumber \]
Essa aproximação se torna arbitrariamente próxima à\(\displaystyle \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}\) medida que aumentamos o número de peças deixando\(m\) e\(S_{ij}\) indo\(n\) para o infinito. Portanto, temos a seguinte equação para calcular integrais de superfície escalar:
\[\iint_S f(x,y,z)\,dS = \iint_D f(\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA. \label{scalar surface integrals} \]
A equação\ ref {integrais de superfície escalar} nos permite calcular uma integral de superfície transformando-a em uma integral dupla. Essa equação para integrais de superfície é análoga à equação para integrais de linha:
\[\iint_C f(x,y,z)\,ds = \int_a^b f(\vecs r(t))||\vecs r'(t)||\,dt. \nonumber \]
Nesse caso, o vetor\(\vecs t_u \times \vecs t_v\) é perpendicular à superfície, enquanto o vetor\(\vecs r'(t)\) é tangente à curva.
Calcular a integral da superfície
\[\iint_S 5 \, dS, \nonumber \]
onde\(S\) está a superfície com parametrização\(\vecs r(u,v) = \langle u, \, u^2, \, v \rangle\) para\(0 \leq u \leq 2\)\(0 \leq v \leq u\) e.
Solução
Observe que esse domínio de parâmetros\(D\) é um triângulo e, portanto, o domínio do parâmetro não é retangular. No entanto, isso não é um problema, porque a Equação\ ref {integrais de superfície escalar} não impõe nenhuma restrição à forma do domínio do parâmetro.
Para usar a Equação\ ref {integrais de superfície escalar} para calcular a integral da superfície, primeiro encontramos vetores\(\vecs t_u\)\(\vecs t_v\) e. Observe isso\(\vecs t_u = \langle 1, 2u, 0 \rangle\)\(\vecs t_v = \langle 0,0,1 \rangle\) e. Portanto,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \nonumber \\ 1 & 2u & 0 \nonumber \\ 0 & 0 & 1 \end{vmatrix} = \langle 2u, \, -1, \, 0 \rangle\ \nonumber \]
e
\[||\vecs t_u \times \vecs t_v|| = \sqrt{1 + 4u^2}. \nonumber \]
Pela equação\ ref {integrais de superfície escalar},
\ [\ begin {align*}\ Iint_s 5\, dS &= 5\ Iint_d\ sqrt {1 + 4u^2}\, dA\\
&= 5\ int_0^2\ int_0^u\ sqrt {1 + 4u^2}\, dv\, du = 5\ int_0^2 u\ sqrt {1 + 4u^2}, du\\
&= 5\ left [\ dfrac {(1+4u^2) ^ {3/2}} {3}\ right] _0^2\\
&=\ dfrac {5 (17^ {3/2} -1)} {3}\ aprox. 115. 15. \ end {align*}\]
Calcular a integral da superfície\[\iint_S (x + y^2) \, dS, \nonumber \] onde\(S\) está o cilindro\(x^2 + y^2 = 4, \, 0 \leq z \leq 3\) (Figura\(\PageIndex{15}\)).
Solução
Para calcular a integral da superfície, primeiro precisamos de uma parametrização do cilindro. Uma parametrização é\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, 0 \leq u \leq 2\pi, \, 0 \leq v \leq 3.\)
Os vetores tangentes são\(\vecs t_u = \langle \sin u, \, \cos u, \, 0 \rangle\)\(\vecs t_v = \langle 0,0,1 \rangle\) e. Então,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \end{vmatrix} = \langle \cos u, \, \sin u, \, 0 \rangle \nonumber \]
\(||\vecs t_u \times \vecs t_v || = \sqrt{\cos^2 u + \sin^2 u} = 1\)e. Pela equação\ ref {integrais de superfície escalar},
\ [\ begin {align*}\ iint_s f (x, y, z) dS &=\ Iint_d f (\ vecs r (u, v)) ||\ vecs t_u\ times\ vecs t_v||\, dA\\
&=\ int_0^3\ int_0^ {2\ pi} (\ cos u +\ sin^2 u)\, du\, dv\\
&=\ int_0^3\ left [\ sin u +\ dfrac {u} {2} -\ dfrac {\ sin (2u)} {4}\ direita] _0^ {2\ pi}\, dv\\
&= \ int_0^3\ pi\, dv = 3\ pi. \ end {align*}\]
Calcule\[\iint_S (x^2 - z) \,dS, \nonumber \] onde\(S\) está a superfície com parametrização\(\vecs r(u,v) = \langle v, \, u^2 + v^2, \, 1 \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3.\)
- Dica
-
Use a Equação\ ref {integrais de superfície escalar}.
- Responda
-
24
\(f(x,y,z) = z^2\)Calcule a integral da superfície\[\iint_S f(x,y,z)\,dS, \nonumber \] onde e\(S\) é a superfície que consiste no pedaço de esfera\(x^2 + y^2 + z^2 = 4\) que está no plano ou acima\(z = 1\) dele e no disco que é delimitado pelo plano de interseção\(z = 1\) e pela esfera dada (Figura\(\PageIndex{16}\)).
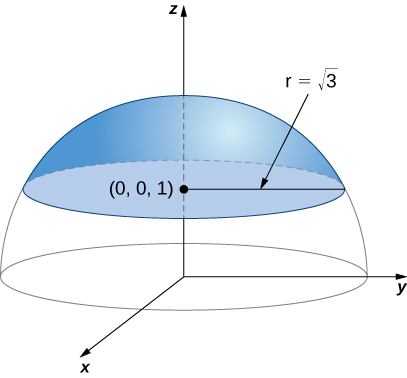
Solução
Observe que não\(S\) é suave, mas é suave por partes;\(S\) pode ser escrito como a união de sua base\(S_1\) e seu topo esférico\(S_2\),\(S_1\) e ambos\(S_2\) são lisos. Portanto, para calcular
\[\iint_S z^2 dS, \nonumber \]
escrevemos essa integral como
\[\iint_{S_1} z^2 \,dS + \iint_{S_2} z^2 \,dS \nonumber \]
e calculamos integrais
\[\iint_{S_1} z^2 \,dS \nonumber \]
e
\[\iint_{S_2}Z^2 \,dS. \nonumber \]
Primeiro, calculamos.\(\displaystyle \iint_{S_1} z^2 \,dS.\) Para calcular essa integral, precisamos de uma parametrização de\(S_1\). Essa superfície é um disco no plano\(z = 1\) centrado em\((0,0,1)\). Para parametrizar esse disco, precisamos saber seu raio. Como o disco é formado onde o plano\(z = 1\) cruza a esfera\(x^2 + y^2 + z^2 = 4\), podemos substituir\(z = 1\) na equação\(x^2 + y^2 + z^2 = 4\):
\[x^2 + y^2 + 1 = 4 \Rightarrow x^2 + y^2 = 3. \nonumber \]
Portanto, o raio do disco é\(\sqrt{3}\) e uma parametrização de\(S_1\) é\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq \sqrt{3}, \, 0 \leq v \leq 2\pi\). Os vetores tangentes são\(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) e\(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, \, 0 \rangle\), e, portanto,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \cos v & \sin v & 0 \\ -u\sin v & u\cos v& 0 \end{vmatrix} = \langle 0, \, 0, u \, \cos^2 v + u \, \sin^2 v \rangle = \langle 0, 0, u \rangle. \nonumber \]
A magnitude desse vetor é\(u\). Portanto,
\ [\ begin {align*}\ iint_ {S_1} z^2\, dS &=\ int_0^ {\ sqrt {3}}\ int_0^ {2\ pi} f (r (u, v)) ||t_u\ times t_v||\, dv\, du\\
&=\ int_0^ {\ sqrt {3}}\ int__0^ {2\ pi} u\, dv\, du\\
&= 2\ pi\ int_0^ {\ sqrt {3}} u\, du\\
&= 2\ pi\ sqrt {3}. \ end {align*}\]
Agora calculamos
\[\iint_{S_2} \,dS. \nonumber \]
Para calcular essa integral, precisamos de uma parametrização de\(S_2\). A parametrização da esfera completa\(x^2 + y^2 + z^2 = 4\) é
\[\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. \nonumber \]
Como estamos apenas pegando o pedaço da esfera no plano ou acima dele\(z = 1\), temos que restringir o domínio de\(\phi\). Para ver até onde esse ângulo se arrasta, observe que o ângulo pode ser localizado em um triângulo reto, conforme mostrado na Figura\(\PageIndex{17}\) (isso\(\sqrt{3}\) vem do fato de que a base de\(S\) é um disco com raio\(\sqrt{3}\)). Portanto, a tangente de\(\phi\) é\(\sqrt{3}\), o que implica que\(\phi\) é\(\pi / 6\). Agora temos uma parametrização de\(S_2\):
\(\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi / 3.\)
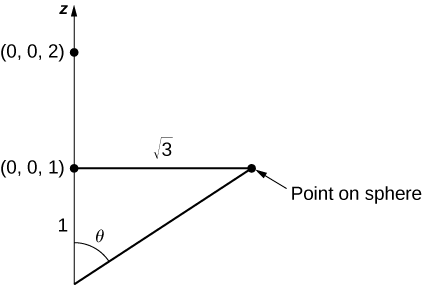
Os vetores tangentes são\(\vecs t_{\phi} = \langle 2 \, \cos \theta \, \cos \phi, \, 2 \, \sin \theta \,\cos \phi, \, -2 \, \sin \phi \rangle\) e\(\vecs t_{\theta} = \langle - 2 \sin \theta \sin \phi, \, u\cos \theta \sin \phi, \, 0 \rangle\), e, portanto,
\ [\ begin {align*}\ vecs t_ {\ phi}\ times\ vecs t_ {\ theta} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\ nonumber\\ 2\ cos\ theta\ cos\ cos\ cos\ cos\ cos\ phi e 2\ sin\ theta\ cos\ phi & -2\ sin\ phi\\ -2\ sin\ theta\ sin\ phi e 2\ cos\ theta\ sin\ phi e 0\ end {vmatrix}\\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ sin^2\ phi,\, 4\,\ sin\ theta\,\ sin^2\ phi,\, 4\,\ cos^2\ theta\,\ cos\ phi\,\ sin\ phi + 4\,\ sin^2\ theta\,\ cos\ phi\,\ sin\ phi\ rangle\\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ sin^2\ phi,\, 4\,\ sin\ theta\,\ sin^2\ phi,\, 4\,\ cos\ phi\,\ sin\ phi\ rangle. \ end {align*}\]
A magnitude desse vetor é
\ [\ begin {align*}\ vecs t_ {\ phi}\ times\ vecs t_ {\ theta} &=\ sqrt {16\,\ cos^2\ theta\,\ sin^4\ phi + 16\,\ sin^2\ theta\,\ sin^4\ phi + 16\,\ cos^2\ phi\,\ sin^2\ phi\,\ sin^2\ phi}\\ [4 pt]
&= 4\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}. \ end {align*}\]
Portanto,
\ [\ begin {align*}\ iint_ {S_2} z\, dS &=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} f (\ vecs r (\ phi,\ theta)) ||\ vecs t_ {\ phi}\ times\ vecs t_ {\ theta} ||\, d\ theta\, d\ pheta\, d\ phi}\ i\\
&=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} 16\,\ cos^2\ phi\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ theta\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\,\ sin\ phi\ sqrt\ sin^2\ phi +\ cos^2\ phi}\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\,\ sin\ phi\, d\ phi\\
& = 32\ pi\ left [-\ dfrac {\ cos^3\ phi} {3}\ direita] _0^ {\ pi/6}\\
&= 32\ pi\ left [\ dfrac {1} {3} -\ dfrac {\ sqrt {3}} {8}\ direita] =\ dfrac {32\ pi} {3} - 4\ sqrt {3}}. \ end {align*}\]
Desde
\[\iint_S z^2 \,dS = \iint_{S_1}z^2 \,dS + \iint_{S_2}z^2 \,dS, \nonumber \]
nós temos
\[\iint_S z^2 \,dS = (2\pi - 4) \sqrt{3} + \dfrac{32\pi}{3}. \nonumber \]
Análise
Neste exemplo, dividimos uma integral de superfície sobre uma superfície por partes na adição de integrais de superfície sobre subsuperfícies lisas. Havia apenas duas subsuperfícies lisas neste exemplo, mas essa técnica se estende a um número finito de subsuperfícies lisas.
Calcule a integral da linha\(\displaystyle \iint_S (x - y) \, dS,\) onde\(S\) está o cilindro\(x^2 + y^2 = 1, \, 0 \leq z \leq 2\), incluindo a parte superior e inferior circulares.
- Dica
-
Divida a integral em três integrais de superfície separadas.
- Responda
-
0
Integrais de superfície escalar têm várias aplicações no mundo real. Lembre-se de que integrais de linha escalar podem ser usados para calcular a massa de um fio dada sua função de densidade. De forma semelhante, podemos usar integrais de superfície escalar para calcular a massa de uma folha dada sua função de densidade. Se uma fina folha de metal tem a forma da superfície\(S\) e a densidade da folha no ponto\((x,y,z)\) é\(\rho(x,y,z)\), então a massa\(m\) da folha é
\[\displaystyle m = \iint_S \rho (x,y,z) \,dS. \label{mass} \]
Uma folha plana de metal tem a forma de superfície\(z = 1 + x + 2y\) que fica acima do retângulo\(0 \leq x \leq 4\)\(0 \leq y \leq 2\) e. Se a densidade da folha for dada por\(\rho (x,y,z) = x^2 yz\), qual é a massa da folha?
Solução
\(S\)Seja a superfície que descreve a folha. Então, a massa da folha é dada por\(\displaystyle m = \iint_S x^2 yx \, dS.\) Para calcular essa integral de superfície, primeiro precisamos de uma parametrização de\(S\). Como\(S\) é dada pela função\(f(x,y) = 1 + x + 2y\), uma parametrização de\(S\) é\(\vecs r(x,y) = \langle x, \, y, \, 1 + x + 2y \rangle, \, 0 \leq x \leq 4, \, 0 \leq y \leq 2\).
Os vetores tangentes são\(\vecs t_x = \langle 1,0,1 \rangle\)\(\vecs t_y = \langle 1,0,2 \rangle\) e. Portanto,\(\vecs t_x + \vecs t_y = \langle -1,-2,1 \rangle\)\(||\vecs t_x \times \vecs t_y|| = \sqrt{6}\) e.
Pela definição da integral de linha (Seção 16.2),\ [\ begin {align*} m &=\ Iint_s x^2 yz\, dS\\ [4pt]
&=\ sqrt {6}\ int_0^4\ int_0^2 x^2 y (1 + x + 2y)\, dy\, dx\\ [4pt]
&=\ sqrt {6}\ int_0^4\ dfrac {22x^2} {3} + 2x^3\, dx\\ [4pt]
&=\ dfrac {2560\ sqrt { 6}} {9}\ aproximadamente 696,74. \ end {align*}\]
Uma peça de metal tem uma forma modelada por parabolóide\(z = x^2 + y^2, \, 0 \leq z \leq 4,\) e a densidade do metal é dada por\(\rho (x,y,z) = z + 1\). Encontre a massa da peça de metal.
- Dica
-
A massa de uma folha é dada pela Equação\ ref {mass}. Uma parametrização útil de um parabolóide foi dada em um exemplo anterior.
- Responda
-
\(38.401 \pi \approx 120.640\)
Orientação de uma superfície
Lembre-se de que, quando definimos uma integral de linha escalar, não precisávamos nos preocupar com a orientação da curva de integração. O mesmo aconteceu com integrais de superfície escalar: não precisávamos nos preocupar com uma “orientação” da superfície de integração.
Por outro lado, quando definimos integrais de linha vetorial, a curva de integração precisava de uma orientação. Ou seja, precisávamos da noção de uma curva orientada para definir uma integral de linha vetorial sem ambigüidade. Da mesma forma, quando definimos uma superfície integral de um campo vetorial, precisamos da noção de uma superfície orientada. Uma superfície orientada recebe uma orientação “para cima” ou “para baixo” ou, no caso de superfícies como uma esfera ou cilindro, uma orientação “para fora” ou “para dentro”.
Deixe S ser uma superfície lisa. Para qualquer ponto\((x,y,z)\)\(S\), podemos identificar dois vetores normais unitários\(\vecs N\)\(-\vecs N\) e. Se for possível escolher um vetor normal unitário\(\vecs N\) em cada ponto\((x,y,z)\), de forma que\(\vecs N\) varie continuamente\(S\), então\(S\) é “orientável”.\(S\) Essa escolha do vetor normal unitário em cada ponto fornece a orientação de uma superfície\(S\). Se você pensar no campo normal como uma descrição do fluxo de água, então o lado da superfície para o qual a água flui é o lado “negativo” e o lado da superfície em que a água flui é o lado “positivo”. Informalmente, uma escolha de orientação fornece\(S\) um lado “externo” e um lado “interno” (ou um lado “para cima” e um lado “para baixo”), assim como a escolha da orientação de uma curva dá à curva as direções “para frente” e “para trás”.
Superfícies fechadas, como esferas, são orientáveis: se escolhermos o vetor normal externo em cada ponto da superfície da esfera, os vetores normais unitários variam continuamente. Isso é chamado de orientação positiva da superfície fechada (Figura\(\PageIndex{18}\)). Também poderíamos escolher o vetor normal interno em cada ponto para dar uma orientação “interna”, que é a orientação negativa da superfície.
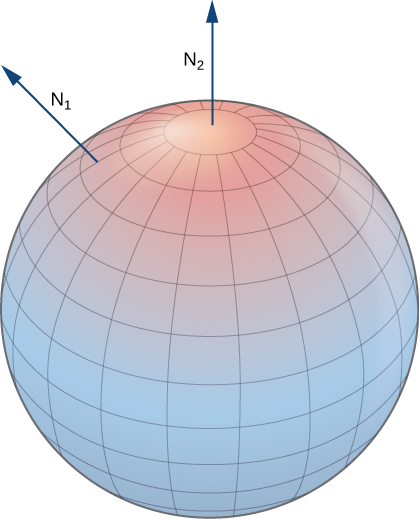
Uma parte do gráfico de qualquer função suave também\(z = f(x,y)\) é orientável. Se escolhermos o vetor normal unitário que aponta “acima” da superfície em cada ponto, os vetores normais unitários variam continuamente sobre a superfície. Também podemos escolher o vetor normal unitário que aponta “abaixo” da superfície em cada ponto. Para obter essa orientação, parametrizamos o gráfico\(f\) de da maneira padrão:\(\vecs r(x,y) = \langle x,\, y, \, f(x,y)\rangle\), onde\(x\) e\(y\) variamos no domínio de\(f\). Então,\(\vecs t_x = \langle 1,0,f_x \rangle\) e\(\vecs t_y = \langle 0,1,f_y \rangle \), portanto, o produto cruzado\(\vecs t_x \times \vecs t_y\) (que é normal para a superfície em qualquer ponto da superfície) é\(\langle -f_x, \, -f_y, \, 1 \rangle \) Como o\(z\) componente -desse vetor é um, a unidade correspondente do vetor normal aponta “para cima” e o lado ascendente da superfície é escolhido para seja o lado “positivo”.
\(S\)Seja uma superfície lisa e orientável com parametrização\(\vecs r(u,v)\). Para cada ponto\(\vecs r(a,b)\) na superfície, os\(\vecs t_u\) vetores\(\vecs t_v\) estão no plano tangente nesse ponto. \(\vecs t_u \times \vecs t_v\)O vetor é normal ao plano tangente em\(\vecs r(a,b)\) e, portanto, é normal a esse\(S\) ponto. Portanto, a escolha do vetor normal unitário
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
fornece uma orientação da superfície\(S\).
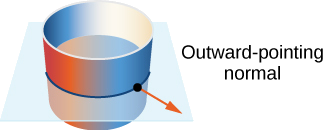
Dê uma orientação do cilindro\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\).
Solução
Esta superfície tem parametrização\(\vecs r(u,v) = \langle r \, \cos u, \, r \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h.\)
Os vetores tangentes são\(\vecs t_u = \langle -r \, \sin u, \, r \, \cos u, \, 0 \rangle \)\(\vecs t_v = \langle 0,0,1 \rangle\) e. Para obter uma orientação da superfície, calculamos o vetor normal unitário
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
Nesse caso,\(\vecs t_u \times \vecs t_v = \langle r \, \cos u, \, r \, \sin u, \, 0 \rangle\) e, portanto,
\[||\vecs t_u \times \vecs t_v|| = \sqrt{r^2 \cos^2 u + r^2 \sin^2 u} = r. \nonumber \]
Uma orientação do cilindro é
\[\vecs N(u,v) = \dfrac{\langle r \, \cos u, \, r \, \sin u, \, 0 \rangle }{r} = \langle \cos u, \, \sin u, \, 0 \rangle. \nonumber \]
Observe que todos os vetores são paralelos ao\(xy\) plano -, o que deve ser o caso dos vetores que são normais ao cilindro. Além disso, todos os vetores apontam para fora e, portanto, essa é uma orientação externa do cilindro (Figura\(\PageIndex{19}\)).
Dê a orientação “ascendente” do gráfico de\(f(x,y) = xy\).
- Dica
-
Parametrize a superfície e use o fato de que a superfície é o gráfico de uma função.
- Responda
-
\[\vecs{N}(x,y) = \left\langle \dfrac{-y}{\sqrt{1+x^2+y^2}}, \, \dfrac{-x}{\sqrt{1+x^2+y^2}}, \, \dfrac{1}{\sqrt{1+x^2+y^2}} \right\rangle \nonumber \]
Como toda curva tem uma direção “para frente” e “para trás” (ou, no caso de uma curva fechada, no sentido horário e anti-horário), é possível orientar qualquer curva. Portanto, é possível pensar em cada curva como uma curva orientada. No entanto, esse não é o caso das superfícies. Algumas superfícies não podem ser orientadas; essas superfícies são chamadas de não orientáveis. Essencialmente, uma superfície pode ser orientada se a superfície tiver um lado “interno” e um lado “externo”, ou um lado “para cima” e um lado “para baixo”. Algumas superfícies são torcidas de tal forma que não há uma noção bem definida de um lado “interno” ou “externo”.
O exemplo clássico de uma superfície não orientável é a faixa de Möbius. Para criar uma tira Möbius, pegue uma tira retangular de papel, dê meia torção no pedaço de papel e cole as pontas (Figura\(\PageIndex{20}\)). Por causa da meia torção na faixa, a superfície não tem lado “externo” ou lado “interno”. Se você imaginar colocar um vetor normal em um ponto da faixa e fazer com que o vetor viaje ao redor da banda, então (por causa da meia torção) o vetor aponta na direção oposta quando volta à sua posição original. Portanto, a faixa realmente tem apenas um lado.

Como algumas superfícies não são orientáveis, não é possível definir uma superfície vetorial integral em todas as superfícies lisas por partes. Isso contrasta com as integrais de linha vetorial, que podem ser definidas em qualquer curva suave por partes.
Integral de superfície de um campo vetorial
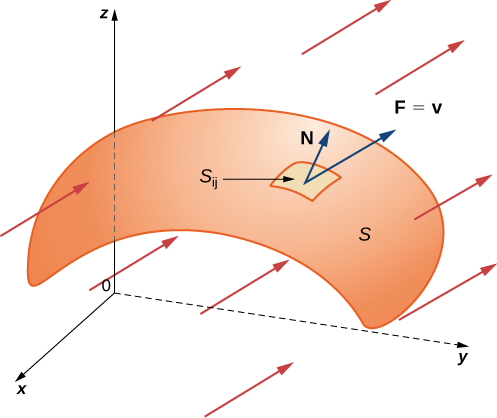
Com a ideia de superfícies orientáveis no lugar, agora estamos prontos para definir uma superfície integral de um campo vetorial. A definição é análoga à definição do fluxo de um campo vetorial ao longo de uma curva plana. Lembre-se de que se\(\vecs{F}\) for um campo vetorial bidimensional e\(C\) uma curva plana, então a definição do fluxo de\(\vecs{F}\) longo\(C\) envolve cortar\(C\) em pequenos pedaços, escolher um ponto dentro de cada peça e calcular\(\vecs{F} \cdot \vecs{N}\) no ponto (onde\(\vecs{N}\) está o vetor normal unitário no ponto). A definição de uma superfície integral de um campo vetorial ocorre da mesma forma, exceto que agora cortamos a superfície\(S\) em pequenos pedaços, escolhemos um ponto na peça pequena (bidimensional) e calculamos\(\vecs{F} \cdot \vecs{N}\) no ponto.
Para colocar essa definição em uma configuração do mundo real,\(S\) seja uma superfície orientada com vetor normal unitário\(\vecs{N}\). \(\vecs{v}\)Seja o campo de velocidade de um fluido\(S\) fluindo e suponha que o fluido tenha densidade\(\rho(x,y,z)\) Imagine que o fluido flui\(S\), mas\(S\) é completamente permeável para não impedir o fluxo do fluido (Figura\(\PageIndex{21}\)). O fluxo de massa do fluido é a taxa de fluxo de massa por unidade de área. O fluxo de massa é medido em massa por unidade de tempo por unidade de área. Como podemos calcular o fluxo de massa do fluido\(S\)?
A taxa de fluxo, medida em massa por unidade de tempo por unidade de área, é\(\rho \vecs N\). Para calcular o fluxo de massa transversal\(S\), corte\(S\) em pedaços pequenos\(S_{ij}\). Se\(S_{ij}\) for pequeno o suficiente, então ele pode ser aproximado por um plano tangente\(P\) em algum ponto\(S_{ij}\). Portanto, o vetor normal unitário at\(P\) pode ser usado para aproximar\(\vecs N(x,y,z)\) toda a peça\(S_{ij}\) porque o vetor normal para um plano não muda à medida que nos movemos pelo plano. O componente do vetor\(\rho v\) em P na direção de\(\vecs{N}\) está\(\rho \vecs v \cdot \vecs N\) em\(P\). Como\(S_{ij}\) é pequeno, o produto escalar\(\rho v \cdot N\) muda muito pouco à medida que variamos\(S_{ij}\) e, portanto,\(\rho \vecs v \cdot \vecs N\) pode ser considerado aproximadamente constante\(S_{ij}\). Para aproximar a massa de fluido por unidade de tempo fluindo\(S_{ij}\) (e não apenas localmente no ponto\(P\)), precisamos multiplicar\((\rho \vecs v \cdot \vecs N) (P)\) pela área de\(S_{ij}\). Portanto, a massa de fluido por unidade de tempo fluindo\(S_{ij}\) na direção de\(\vecs{N}\) pode ser aproximada por\((\rho \vecs v \cdot \vecs N)\Delta S_{ij}\) onde\(\vecs{N}\),\(\rho\) e todas\(\vecs{v}\) são avaliadas em\(P\) (Figura\(\PageIndex{22}\)). Isso é análogo ao fluxo do campo\(\vecs{F}\) vetorial bidimensional na curva plana\(C\), no qual aproximamos o fluxo em um pequeno pedaço\(C\) com a expressão\((\vecs{F} \cdot \vecs{N}) \,\Delta s\). Para aproximar o fluxo de massa\(S\), forme a soma
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
À medida que as peças\(S_{ij}\) ficam menores, a soma
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij} \nonumber \]
fica arbitrariamente próximo do fluxo de massa. Portanto, o fluxo de massa é
\[\iint_s \rho \vecs v \cdot \vecs N \, dS = \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Essa é uma superfície integral de um campo vetorial. Deixar o campo vetorial\(\rho \vecs{v}\) ser um campo vetorial arbitrário\(\vecs{F}\) leva à seguinte definição.
\(\vecs{F}\)Seja um campo vetorial contínuo com um domínio que contém superfície orientada\(S\) com vetor normal unitário\(\vecs{N}\). A parte integral da superfície de\(\vecs{F}\) over\(S\) é
\[\iint_S \vecs{F} \cdot \vecs{S} = \iint_S \vecs{F} \cdot \vecs{N} \,dS. \label{surfaceI} \]
Observe o paralelo entre essa definição e a definição de integral de linha vetorial\(\displaystyle \int_C \vecs F \cdot \vecs N\, dS\). Uma integral de superfície de um campo vetorial é definida de forma semelhante a uma integral de linha de fluxo em uma curva, exceto que o domínio de integração é uma superfície (um objeto bidimensional) em vez de uma curva (um objeto unidimensional). Integral\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) é chamado de fluxo\(\vecs{F}\) transversal\(S\), assim como integral\(\displaystyle \int_C \vecs F \cdot \vecs N\,dS\) é o fluxo da curva\(\vecs F\) transversal\(C\). Uma integral de superfície sobre um campo vetorial também é chamada de integral de fluxo.
Assim como com integrais de linha vetorial, a integral de superfície\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) é mais fácil de calcular após a superfície ter\(S\) sido parametrizada. \(\vecs r(u,v)\)Seja uma parametrização de\(S\) com domínio de parâmetros\(D\). Então, o vetor normal unitário é dado por\(\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||}\) e, da Equação\ ref {surfaceI}, temos
\ [\ begin {align*}\ int_C\ vecs F\ cdot\ vecs N\, dS &=\ Iint_s\ vecs F\ cdot\ dfrac {\ vecs t_u\ times\ vecs t_v} {||\ vecs t_u\ times\ vecs t_v||}\, dS\\ [4pt]
&=\ iInt_d\ esquerda (\ vecs F (\ vecs r (u, v))\ cdot\ dfrac {\ vecs t_u\ times\ vecs t_v} {||\ vecs t_u\ times\ vecs t_v||}\ direita) ||\ vecs t_u \ times\ vecs t_v ||\, dA\\ [4pt]
&=\ Iint_d (\ vecs F (\ vecs r (u, v))\ cdot (\ vecs t_u\ times\ vecs t_v))\, dA. \ end {align*}\]
Portanto, para calcular uma integral de superfície sobre um campo vetorial, podemos usar a equação
\[\iint_S \vecs F \cdot \vecs N\, dS = \iint_D (\vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v)) \,dA. \label{equation 5} \]
Calcule a integral da superfície
\[\iint_S \vecs F \cdot \vecs N\,dS, \nonumber \]
onde\(\vecs{F} = \langle -y,x,0\rangle\) e\(S\) é a superfície com parametrização
\[\vecs r(u,v) = \langle u,v^2 - u, \, u + v\rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 4. \nonumber \]
Solução
Os vetores tangentes são\(\vecs t_u = \langle 1,-1,1\rangle\)\(\vecs t_v = \langle 0,2v,1\rangle\) e. Portanto,
\[\vecs t_u \times \vecs t_v = \langle -1 -2v, -1, 2v\rangle. \nonumber \]
Pela equação\ ref {equação 5},
\[ \begin{align*} \iint_S \vecs F \cdot dS &= \int_0^4 \int_0^3 F (\vecs r(u,v)) \cdot (\vecs t_u \times \vecs t_v) \, du \,dv \\[4pt] &= \int_0^4 \int_0^3 \langle u - v^2, \, u, \, 0\rangle \cdot \langle -1 -2v, \, -1, \, 2v\rangle \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 [(u - v^2)(-1-2v) - u] \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 (2v^3 + v^2 - 2uv - 2u) \, du\,dv \\[4pt] &= \int_0^4 \left.[2v^3u + v^2u - vu^2 - u^2]\right|_0^3 \, dv \\[4pt] &= \int_0^4 (6v^3 + 3v^2 - 9v - 9) \, dv \\[4pt] &= \left[ \dfrac{3v^4}{2} + v^3 - \dfrac{9v^2}{2} - 9v\right]_0^4\\[4pt] &= 340. \end{align*}\]
Portanto, o fluxo de\(\vecs{F}\) cruzamento\(S\) é 340.
\(\vecs F = \langle 0, -z, y \rangle\)Calcule a integral da superfície\[\iint_S \vecs F \cdot \vecs N \, dS, \nonumber \] onde e\(S\) é a porção da esfera unitária no primeiro octante com orientação externa.
- Dica
-
Use a Equação\ ref {equação 5}.
- Responda
-
0
Vamos\(\vecs v(x,y,z) = \langle 2x, \, 2y, \, z\rangle\) representar um campo de velocidade (com unidades de metros por segundo) de um fluido com densidade constante 80 kg/m 3. \(S\)Seja um hemisfério\(x^2 + y^2 + z^2 = 9\) com\(z \leq 0\) um que\(S\) esteja orientado para fora. Encontre a taxa de fluxo de massa do fluido\(S\).
Solução
A parametrização da superfície é
\[\vecs r(\phi, \theta) = \langle 3 \, \cos \theta \, \sin \phi, \, 3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi/2. \nonumber \]
Como no exemplo, os vetores tangentes são\(\vecs t_{\theta} = \langle -3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \theta \, \sin \phi, \, 0 \rangle \) e\( \vecs t_{\phi} = \langle 3 \, \cos \theta \, \cos \phi, \, 3 \, \sin \theta \, \cos \phi, \, -3 \, \sin \phi \rangle,\) e seu produto cruzado é
\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle. \nonumber \]
Observe que cada componente do produto cruzado é positivo e, portanto, esse vetor fornece a orientação externa. Portanto, usamos a orientação
\(\vecs N = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle \)
para a esfera.
Por\ label {surfaceI},
\ [\ begin {align*}\ Iint_s\ rho v\ cdot\, dS &= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} v (r (\ phi,\ theta))\ cdot (t_ {\ phi}\ times t_ {\ theta})\, d\ phi\, d\ theta\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2}\ langle 6\,\ cos\ theta\,\ sin\ phi,\, 6\,\ sin\ theta\,\ sin\ phi,\, 3\,\ cos\ phi\ rangle\ cdot\ langle 9\,\ cos\ theta\,\ sin^2\ phi,\, 9\,\ sin\ theta\,\ sin^2\ phi,\, 9\,\ sin\ phi\,\ cos\ phi\ rangle\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ sin^3\ phi + 27\,\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54 (1 -\ cos^2\ phi)\,\ sin\ phi + 27\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ sin\ phi - 27,\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ Grande [-54\,\ cos\ phi + 9\,\ cos^3\ phi\ Big] _ {\ phi =0} ^ {\ phi=2\ pi}\, d\ theta\\
&=80\ int_0^ {2\ pi} 45\, d\ theta\\
&= 7200\ pi. \ end {align*}\ nonumber\]
Portanto, a taxa de fluxo de massa é\(7200\pi \, \text{kg/sec/m}^2\).
Deixe\(\vecs v(x,y,z) = \langle x^2 + y^2, \, z, \, 4y \rangle\) m/seg representar um campo de velocidade de um fluido com densidade constante de 100 kg/m 3. \(S\)Seja o meio cilindro\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) orientado para fora. Calcule o fluxo de massa do fluido transversalmente\(S\).
- Dica
-
Use\ label {surfaceI}.
- Responda
-
400 kg/seg/m
No exemplo\(\PageIndex{14}\), calculamos o fluxo de massa, que é a taxa de fluxo de massa por unidade de área. Se quisermos encontrar a taxa de fluxo (medida em volume por tempo), podemos usar a integral de fluxo
\[\iint_S \vecs v \cdot \vecs N \, dS, \nonumber \]
o que deixa de fora a densidade. Como a vazão de um fluido é medida em volume por unidade de tempo, a vazão não leva em consideração a massa. Portanto, temos a seguinte caracterização da taxa de fluxo de um fluido com velocidade\(\vecs v\) em uma superfície\(S\):
\[\text{Flow rate of fluid across S} = \iint_S \vecs v \cdot dS. \nonumber \]
Para calcular a taxa de fluxo do fluido no exemplo, simplesmente removemos a constante de densidade, que fornece uma taxa de fluxo de\(90 \pi \, m^3/sec\).
Tanto o fluxo de massa quanto a taxa de fluxo são importantes em física e engenharia. O fluxo de massa mede a quantidade de massa que está fluindo em uma superfície; a taxa de fluxo mede quanto volume de fluido está fluindo em uma superfície.
Além de modelar o fluxo de fluido, as integrais de superfície podem ser usadas para modelar o fluxo de calor. Suponha que a temperatura\((x,y,z)\) no ponto de um objeto seja\(T(x,y,z)\). Então, o fluxo de calor é um campo vetorial proporcional ao gradiente negativo de temperatura no objeto. Para ser preciso, o fluxo de calor é definido como campo vetorial\(F = - k \nabla T\), onde a constante k é a condutividade térmica da substância da qual o objeto é feito (essa constante é determinada experimentalmente). A taxa de fluxo de calor através da superfície S no objeto é dada pela integral de fluxo
\[\iint_S \vecs F \cdot dS = \iint_S -k \vecs \nabla T \cdot dS. \nonumber \]
Um cilindro sólido de ferro fundido é dado por desigualdades\(x^2 + y^2 \leq 1, \, 1 \leq z \leq 4\). A temperatura em um ponto\((x,y,z)\) em uma região que contém o cilindro é\(T(x,y,z) = (x^2 + y^2)z\). Dado que a condutividade térmica do ferro fundido é 55, determine o fluxo de calor através do limite do sólido se esse limite estiver orientado para fora.
Solução
Vamos\(S\) indicar o limite do objeto. Para encontrar o fluxo de calor, precisamos calcular a integral do fluxo.\[\iint_S -k\vecs \nabla T \cdot dS. \nonumber \] Observe que não\(S\) é uma superfície lisa, mas é lisa por partes, pois\(S\) é a união de três superfícies lisas (a parte superior e inferior circulares e o lado cilíndrico). Portanto, calculamos três integrais separadas, uma para cada peça lisa de\(S\). Antes de calcular qualquer integral, observe que o gradiente da temperatura é\(\vecs \nabla T = \langle 2xz, \, 2yz, \, x^2 + y^2 \rangle\).
Primeiro, consideramos a parte inferior circular do objeto, que denotamos\(S_1\). Podemos ver que\(S_1\) é um círculo de raio 1 centrado no ponto\((0,0,1)\) sentado no plano\(z = 1\). Esta superfície tem parametrização\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 1 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Portanto,
\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\)e\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle\),\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0, \, 0, -v \rangle\) e.
Como a superfície está orientada para fora e\(S_1\) é a parte inferior do objeto, faz sentido que esse vetor aponte para baixo. Por equação, o fluxo de calor\(S_1\) é
\[ \begin{align*}\iint_{S_1} -k \vecs \nabla T \cdot dS &= - 55 \int_0^{2\pi} \int_0^1 \vecs \nabla T(u,v) \cdot (\vecs t_u \times \vecs t_v) \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2 \cos^2 u + v^2 \sin^2 u \rangle \cdot \langle 0,0, -v\rangle \, dv \,du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2\rangle \cdot \langle 0, 0, -v \rangle \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 -v^3 \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} -\dfrac{1}{4} du \\[4pt] &= \dfrac{55\pi}{2}.\end{align*}\]
Agora vamos considerar a parte superior circular do objeto, que denotamos\(S_2\). Vemos que\(S_2\) é um círculo de raio 1 centrado no ponto\((0,0,4)\), sentado no plano\(z = 4\). Esta superfície tem parametrização\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 4 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Portanto,\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\) e\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle \),\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0,0,-v\rangle\) e.
Como a superfície é orientada para fora e\(S_1\) é a parte superior do objeto, em vez disso, tomamos o vetor\(\vecs t_v \times \vecs t_u = \langle 0,0,v\rangle\). Por equação, o fluxo de calor\(S_1\) é
\ [\ begin {align*}\ iint_ {S_2} -k\ vecs\ nabla T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_0^1\ vecs\ nabla T (u, v)\ cdot\, (\ vecs t_u\ times\ vecs t_v)\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ cos^2 u + v^2\ sin^2 u\ rangle\ cdot\ langle 0,0, -v\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ rangle\ cdot\ langle 0, 0, -v\ rangle\,\, dv\, du\\ [4 pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 -v^3\, dv\, du = - 55\ int_0^ {2\ pi} -\ dfrac {1} {4}\, du = -\ dfrac {55\ pi} {2}. \ end {align*}\]
Por último, vamos considerar o lado cilíndrico do objeto. Essa superfície tem parametrização\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 1 \leq v \leq 4\). Por exemplo, sabemos disso\(\vecs t_u \times \vecs t_v = \langle \cos u, \, \sin u, \, 0 \rangle\). Por equação,
\ [\ begin {align*}\ iint_ {S_3} -k\ vecs\ nabla T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_1^4\ vecs\ nabla T (u, v)\ cdot (\ vecs t_u\ times\ vecs t_v)\, dv\, du\\ [4pt]
= - 55\ int_0^ {2\ pi}\ int_1^4\ langle 2v\,\ cos u,\, 2v\,\ sin u,\ cos^2 u +\ sin^2 u\ rangle\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 2v\,\ cos^2 u,\, 2v\,\ sin u,\, 1\ rangle\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, dv\,\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 (2v\,\ cos^2 u + 2v\,\ sin^2 u)\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 2v\, dv\, du\\ [4pt]
&= -55\ int_0^ {2\ pi} du\\ [4pt]
&= -110\ pi. \ end {align*}\]
Portanto, a taxa de fluxo de calor\(S\) é
\[\dfrac{55\pi}{2} - \dfrac{55\pi}{2} - 110\pi = -110\pi. \nonumber \]
Uma bola sólida de ferro fundido é dada pela desigualdade\(x^2 + y^2 + z^2 \leq 1\). A temperatura em um ponto em uma região que contém a bola é\(T(x,y,z) = \dfrac{1}{3}(x^2 + y^2 + z^2)\). Encontre o fluxo de calor através do limite do sólido se esse limite estiver orientado para fora.
- Dica
-
Siga as etapas do Exemplo\(\PageIndex{15}\).
- Responda
-
\(-\dfrac{440\pi}{3}\)
Conceitos-chave
- As superfícies podem ser parametrizadas, assim como as curvas podem ser parametrizadas. Em geral, as superfícies devem ser parametrizadas com dois parâmetros.
- Às vezes, as superfícies podem ser orientadas, assim como as curvas podem ser orientadas. Algumas superfícies, como uma faixa de Möbius, não podem ser orientadas.
- Uma integral de superfície é como uma integral de linha em uma dimensão superior. O domínio de integração de uma integral de superfície é uma superfície em um plano ou espaço, em vez de uma curva em um plano ou espaço.
- O integrando de uma integral de superfície pode ser uma função escalar ou um campo vetorial. Para calcular uma integral de superfície com um integrando que é uma função, use Equação. Para calcular uma integral de superfície com um integrando que é um campo vetorial, use Equação.
- Se\(S\) for uma superfície, então a área de\(S\) é\[\iint_S \, dS. \nonumber \]
Equações-chave
- Uma superfície calar integral
\[\iint_S f(x,y,z) \,dS = \iint_D f (\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA \nonumber \]
- Fluxo integral
\[\iint_S \vecs F \cdot \vecs N \, dS = \iint_S \vecs F \cdot dS = \iint_D \vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \nonumber \]
Glossário
- integral de fluxo
- outro nome para uma superfície integral de um campo vetorial; o termo preferido em física e engenharia
- curvas de grade
- curvas em uma superfície que são paralelas às linhas de grade em um plano coordenado
- fluxo de calor
- um campo vetorial proporcional ao gradiente negativo de temperatura em um objeto
- fluxo de massa
- a taxa de fluxo de massa de um fluido por unidade de área, medida em massa por unidade de tempo por unidade de área
- orientação de uma superfície
- se uma superfície tem um lado “interno” e um lado “externo”, então uma orientação é uma escolha do lado interno ou externo; a superfície também pode ter orientações “para cima” e “para baixo”
- domínio de parâmetros (espaço de parâmetros)
- a região do\(uv\) plano -sobre a qual os parâmetros\(u\)\(v\) variam para parametrização\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\)
- superfície parametrizada (superfície paramétrica)
- uma superfície dada por uma descrição do formulário\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\), em que\(u\) os parâmetros\(v\) variam em um domínio de parâmetros no\(uv\) plano -
- parametrização regular
- parametrização de\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\) forma que não\(r_u \times r_v\) seja zero para o ponto\((u,v)\) no domínio do parâmetro
- área de superfície
- a área da superfície\(S\) dada pela integral da superfície\[\iint_S \,dS \nonumber \]
- superfície integral
- uma integral de uma função sobre uma superfície
- integral de superfície de uma função de valor escalar
- uma integral de superfície na qual o integrando é uma função escalar
- integral de superfície de um campo vetorial
- uma integral de superfície na qual o integrando é um campo vetorial



Resulta do exemplo\(\PageIndex{1}\) que podemos parametrizar todos os cilindros do formulário\(x^2 + y^2 = R^2\). Se S é um cilindro dado pela equação\(x^2 + y^2 = R^2\), então uma parametrização de\(S\) é\(\vecs r(u,v) = \langle R \, \cos u, \, R \, \sin u, \, v \rangle, \, 0 \leq u \leq 2 \pi, \, -\infty < v < \infty.\)
Também podemos encontrar diferentes tipos de superfícies devido à sua parametrização, ou podemos encontrar uma parametrização quando recebemos uma superfície.
Exemplo\(\PageIndex{2}\): Describing a Surface
Descreva a superfície\(S\) parametrizada por\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u^2 \rangle, \, 0 \leq u < \infty, \, 0 \leq v < 2\pi\).
Solução
Observe que, se\(u\) for mantida constante, a curva resultante é um círculo de raio\(u\) no plano\(z = u\). Portanto, à medida que\(u\) aumenta, o raio do círculo resultante aumenta. Se\(v\) for mantida constante, a curva resultante é uma parábola vertical. Portanto, esperamos que a superfície seja um parabolóide elíptico. Para confirmar isso, observe que
\[\begin{align*} x^2 + y^2 &= (u \, \cos v)^2 + (u \, \sin v)^2 \\[4pt] &= u^2 \cos^2 v + u^2 sin^2 v \\[4pt] &= u^2 \\[4pt] &=z\end{align*}\]
Portanto, a superfície é o parabolóide elíptico\(x^2 + y^2 = z\) (Figura\(\PageIndex{3}\)).
Exercício\(\PageIndex{2}\)
Descreva a superfície parametrizada por\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, - \infty < u < \infty, \, 0 \leq v < 2\pi\).
Mantenha-se\(u\) constante e veja que tipo de curvas resultam. Imagine o que acontece à medida que\(u\) aumenta ou diminui.
Cone\(x^2 + y^2 = z^2\)