15.1: Integrais duplos sobre regiões retangulares
- Page ID
- 188048
- Reconheça quando uma função de duas variáveis é integrável em uma região retangular.
- Reconheça e use algumas das propriedades das integrais duplas.
- Avalie uma integral dupla sobre uma região retangular escrevendo-a como uma integral iterada.
- Use uma integral dupla para calcular a área de uma região, o volume sob uma superfície ou o valor médio de uma função sobre uma região plana.
Nesta seção, investigamos integrais duplas e mostramos como podemos usá-las para encontrar o volume de um sólido sobre uma região retangular no plano xy. Muitas das propriedades das integrais duplas são semelhantes às que já discutimos para integrais simples.
Volumes e integrais duplos
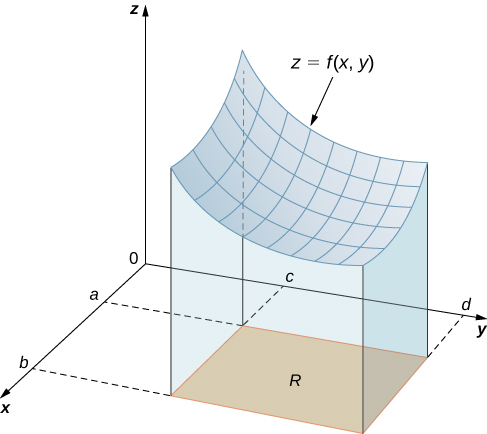
Começamos considerando o espaço acima de uma região retangular\(R\). Considere uma função contínua\(f(x,y)≥0\) de duas variáveis definidas no retângulo fechado\(R\):
\[R=[a,b] \times [c,d]= \left\{(x,y) ∈ \mathbb{R}^2| \, a ≤ x ≤ b, \, c ≤ y ≤ d \right\} \nonumber \]
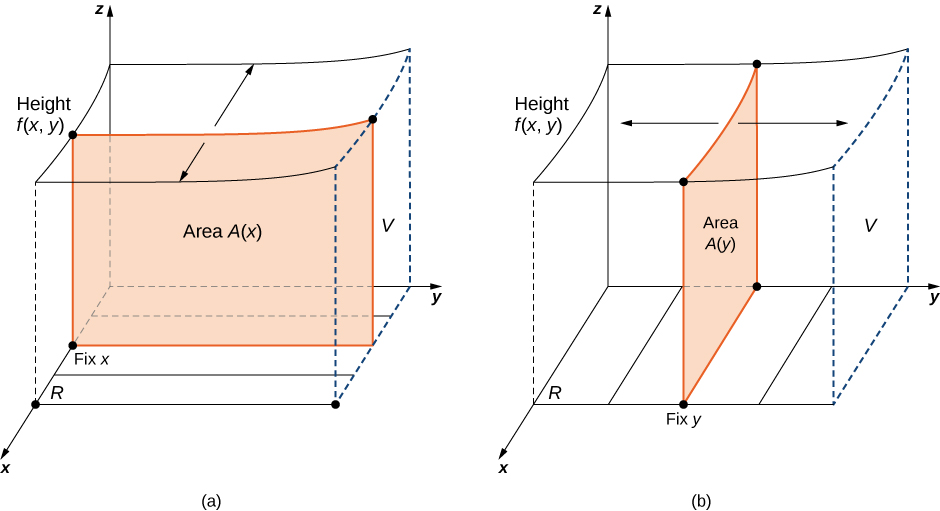
Aqui\([a,b] \times [c,d]\) indica o produto cartesiano dos dois intervalos fechados\([a,b]\)\([c,d]\) e. Consiste em pares retangulares\((x,y)\) como\(a≤x≤b\)\(c≤y≤d\) e. O gráfico de\(f\) representa uma superfície acima do\(xy\) plano -com a equação\(z = f(x,y)\) onde\(z\) é a altura da superfície no ponto\((x,y)\). \(S\)Seja o sólido que está acima\(R\) e abaixo do gráfico de\(f\) (Figura\(\PageIndex{1}\)). A base do sólido é o retângulo\(R\) no\(xy\) plano -. Queremos encontrar o volume\(V\) do sólido\(S\).
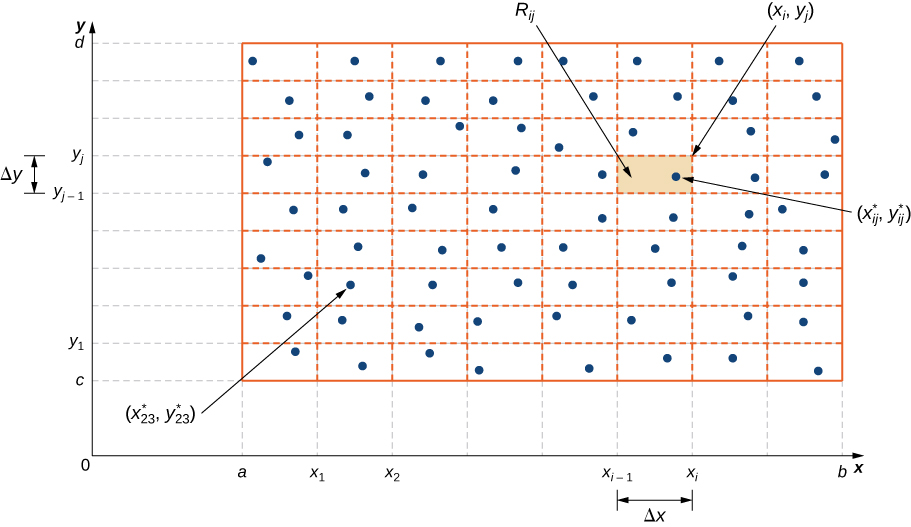
Dividimos a região\(R\) em pequenos retângulos\(R_{ij}\), cada um com área\(ΔA\) e com lados\(Δx\) e\(Δy\) (Figura\(\PageIndex{2}\)). Fazemos isso dividindo o intervalo\([a,b]\) em\(m\) subintervalos e dividindo o intervalo\([c,d]\) em\(n\) subintervalos. Conseqüentemente\(\Delta x = \frac{b - a}{m}\)\(\Delta y = \frac{d - c}{n}\),,\(\Delta A = \Delta x \Delta y\) e.
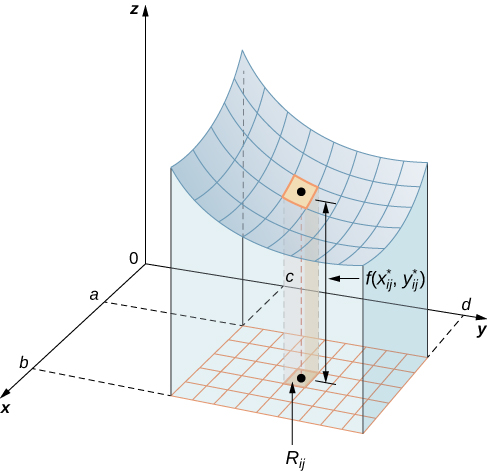
O volume de uma caixa retangular fina acima\(R_{ij}\) é\(f(x_{ij}^*, \, y_{ij}^*)\,\Delta A\), onde (\(x_{ij}^*, \, y_{ij}^*\)) é um ponto de amostra arbitrário em cada uma,\(R_{ij}\) conforme mostrado na figura a seguir,\(f(x_{ij}^*, \, y_{ij}^*)\) é a altura da caixa retangular fina correspondente e\(\Delta A\) é a área de cada retângulo\(R_{ij}\).
Usando a mesma ideia para todos os sub-retângulos, obtemos um volume aproximado do sólido S como
\[V \approx \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Essa soma é conhecida como soma dupla de Riemann e pode ser usada para aproximar o valor do volume do sólido. Aqui, a soma dupla significa que, para cada sub-retângulo, avaliamos a função no ponto escolhido, multiplicamos pela área de cada retângulo e, em seguida, adicionamos todos os resultados.
Como vimos no caso de variável única, obtemos uma melhor aproximação do volume real se\(m\) e nos\(n\) tornamos maiores.
\[V = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*) \Delta A \nonumber \]
ou
\[V=\lim_{\Delta x, \, \Delta y \rightarrow 0} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Observe que a soma se aproxima de um limite em qualquer um dos casos e o limite é o volume do sólido com a base\(R\). Agora estamos prontos para definir a integral dupla.
A integral dupla da função\(f(x, \, y)\) sobre a região retangular\(R\) no\(xy\) plano -é definida como
\[\iint_R f(x, \, y) dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Se\(f(x,y)\geq 0\), then the volume \(V\) of the solid \(S\), which lies above \(R\) in the \(xy\)-plane and under the graph of \(f\), is the double integral of the function \(f(x,y)\) over the rectangle \(R\). If the function is ever negative, then the double integral can be considered a “signed” volume in a manner similar to the way we defined net signed area in a integral definida.
Considere a função\(z = f(x, \, y) = 3x^2 - y\) sobre a região retangular\(R = [0, 2] \times [0, 2]\) (Figura\(\PageIndex{4}\)).
- Configure uma integral dupla para encontrar o valor do volume assinado do sólido\(S\) que está acima\(R\) e “abaixo” do gráfico de\(f\).
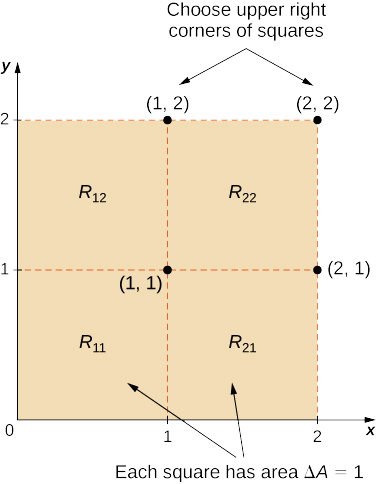
- Divida\(R\) em quatro quadrados com\(m = n = 2\) e escolha o ponto de amostra como o ponto do canto superior direito de cada quadrado (1,1), (2,1), (1,2) e (2,2) (Figura\(\PageIndex{4}\)) para aproximar o volume assinado do sólido\(S\) que está acima\(R\) e “abaixo” do gráfico de\(f\).
- Divida\(R\) em quatro quadrados com\(m = n = 2\) e escolha o ponto de amostra como o ponto médio de cada quadrado: (1/2, 1/2), (3/2, 1/2), (1/2,3/2) e (3/2, 3/2) para aproximar o volume assinado.
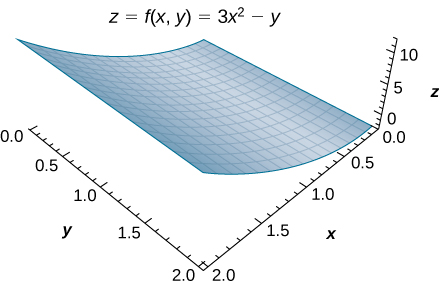
Figura\(\PageIndex{4}\): A função\(z=f(x,y)\) representada graficamente sobre a região retangular\(R=[0,2]×[0,2]\).
Solução
- Como podemos ver, a função\(z = f(x,y) = 3x^2 - y\) está acima do plano. Para encontrar o volume assinado de\(S\), precisamos dividir a região\(R\) em pequenos retângulos\(R_{ij}\), cada um com área\(ΔA\) e com lados e\(Δy\),\(Δx\) e escolher\((x_{ij}^*, y_{ij}^*)\) como pontos de amostra em cada um\(R_{ij}\). Portanto, uma integral dupla é configurada como
\[V = \iint_R (3x^2 - y) dA = \lim_{m,n→∞} \sum_{i=1}^m \sum_{j=1}^n [3(x_{ij}^*)^2 - y_{ij}^*] \Delta A. \nonumber \]
- Aproximando o volume assinado usando uma soma de Riemann com\(m = n = 2\) nós temos\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). Além disso, os pontos de amostra são (1, 1), (2, 1), (1, 2) e (2, 2) conforme mostrado na figura a seguir.
Conseqüentemente,
\ [\ begin {align*} V &\ approx\ sum_ {i=1} ^2\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
&=\ sum_ {i=1} ^2 (f (x_ {i1} ^*, y_ {i1} ^*) + f (x_ {i2} ^*, y_ {i2} ^*))\ Delta A\\ [4pt]
&=f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*)\ Delta UM + f (x_ {22} ^*, y_ {22} ^*)\ Delta A\\ [4pt]
&= f (1,1) (1) + f (2,1) (1) + f (1,2) (1) + f (2,2) (1)\ [4pt]
&= (3 - 1) (1) + (12 - 1) (1) + (1) + (3 - 2) (1) + (12 - 2) (1)\\ [4pt]
&= 2 + 1 + 1 + 10 = 24. \ end {align*}\]
- Aproximando o volume assinado usando uma soma de Riemann com\(m = n = 2\) nós temos\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). Nesse caso, os pontos de amostra são (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) e (3/2, 3/2).
Portanto,
\ [\ begin {align*} V &\ approx\ sum_ {i=1} ^2\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
&=f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*)\ Delta A + f (x_ {22} ^*, y_ {22} ^*)\ Delta A\\ [4pt]
&= f (1/2,1/2) (1) + f (3/2,1/2) (1) + f (1/2,3/2) (1) + f (3/2,3/2) (1)\\ [4pt]
&=\ left (\ frac {3} {4} -\ frac {1} {4}\ direita) (1) +\ esquerda (\ frac {27} {4}} -\ frac {1} {2}\ direita) (1) +\ left (\ frac {3} {4} -\ frac {3} {2}\ direita) (1) +\ left (\ frac {27} {4} -\ frac {3} {2}\ direita) (1)\\ [4pt]
&=\ frac {2} {4} +\ frac {25} {4} +\ left (-\ frac {3} {4}\ direita) +\ frac {21} {4} =\ frac {45} {4} = 11. \ end {align*}\]
Análise
Observe que as respostas aproximadas diferem devido às escolhas dos pontos da amostra. Em ambos os casos, estamos introduzindo algum erro porque estamos usando apenas alguns pontos de amostra. Portanto, precisamos investigar como podemos obter uma resposta precisa.
Use a mesma função\(z = f(x, y) = 3x^2 - y\) na região retangular\(R=[0,2]×[0,2]\).
Divida\(R\) nos mesmos quatro quadrados com\(m = n = 2\) e escolha os pontos de amostra como o ponto do canto superior esquerdo de cada quadrado (0,1), (1,1), (0,2) e (1,2) (Figura\(\PageIndex{5}\)) para aproximar o volume assinado do sólido\(S\) que está acima\(R\) e “abaixo” do gráfico de\(f\).
- Dica
-
Siga as etapas do exemplo anterior.
- Responda
-
\[V \approx \sum_{i=1}^2 \sum_{j=1}^2 f(x_{ij}^*, y_{ij}^*)\,\Delta A = 0 \nonumber \]
Observe que desenvolvemos o conceito de integral dupla usando uma região retangular\(R\). Esse conceito pode ser estendido a qualquer região geral. No entanto, quando uma região não é retangular, os sub-retângulos podem não se encaixar perfeitamente\(R\), especialmente se a área base for curva. Examinaremos essa situação com mais detalhes na próxima seção, onde estudamos regiões que nem sempre são retangulares e os sub-retângulos podem não se encaixar perfeitamente na região\(R\). Além disso, as alturas podem não ser exatas se a superfície\(z=f(x,y)\) for curva. No entanto, os erros nas laterais e a altura em que as peças podem não se encaixar perfeitamente dentro do sólido se\(S\) aproximam de 0\(m\) e se\(n\) aproximam do infinito. Além disso, a integral dupla da função\(z=f(x,y)\) existe desde que a função não\(f\) seja muito descontínua. Se a função for limitada e contínua,\(R\) exceto em um número finito de curvas suaves, então a integral dupla existe e dizemos que ff é integrável\(R\).
Desde então\(\Delta A = \Delta x \Delta y = \Delta y \Delta x\), podemos expressar\(dA\) como\(dx \, dy\) ou\(dy \, dx\). Isso significa que, quando estamos usando coordenadas retangulares, a integral dupla sobre uma região\(R\) denotada por
\[\iint_R f(x,y)\,dA \nonumber \]
pode ser escrito como
\[\iint_R f(x,y)\,dx\,dy \nonumber \]
ou
\[\iint_R f(x,y)\,dy\,dx. \nonumber \]
Agora, vamos listar algumas das propriedades que podem ser úteis para calcular integrais duplos.
Propriedades das integrais duplas
As propriedades das integrais duplas são muito úteis ao computá-las ou trabalhar com elas. Listamos aqui seis propriedades de integrais duplas. As propriedades 1 e 2 são chamadas de linearidade da integral, a propriedade 3 é a aditividade da integral, a propriedade 4 é a monotonicidade da integral e a propriedade 5 é usada para encontrar os limites da integral. A propriedade 6 é usada se\(f(x,y)\) for um produto de duas funções\(g(x)\)\(h(y)\) e.
Suponha que as funções\(f(x,y)\) e\(g(x,y)\) sejam integráveis sobre a região retangular\(R\);\(S\) e\(T\) sejam sub-regiões de\(R\); e suponha que\(m\)\(M\) sejam números reais.
- A soma\(f(x,y)+g(x,y)\) é integrável e
\[\iint_R [f(x, y) + g(x, y)]\,dA = \iint_R f(x,y)\, dA + \iint_R g(x, y) \,dA. \nonumber \]
- Se c é uma constante, então\(cf(x,y)\) é integrável e
\[\iint_R cf(x,y)\,dA = c\iint_R f(x,y)\,dA. \nonumber \]
- Se\(R=S∪T\) e\(S∩T=∅\) exceto uma sobreposição nos limites, então
\[\iint_R f(x,y)\,dA = \iint_S f(x,y) \,dA + \iint_T f(x,y)\, dA. \nonumber \]
- Se for\(f(x,y) \geq g(x,y)\) para\((x,y)\) dentro\(R\), então
\[\iint_R f(x,y)\,dA \geq \iint_R g(x,y)\,dA. \nonumber \]
- Se\(m \leq f(x,y) \leq M\) e\(A(R) = \, \text{the area of}\,R\), então
\[m \cdot A(R) \leq \iint_R f(x,y)\,dA \leq M \cdot A(R). \nonumber \]
- No caso em que\(f(x,y)\) pode ser fatorado como um produto de uma função\(g(x)\) de\(x\) apenas e uma função\(h(y)\) de\(y\) apenas, então, sobre a região\(R = \big\{(x,y) \,|\,a \leq x \leq b, \, c \leq y \leq d \big\}\), a integral dupla pode ser escrita como
\[\iint_R f(x,y)\,dA = \left(\int_a^b g(x)\,dx \right)\left(\int_c^d h(y) \,dy \right). \nonumber \]
Essas propriedades são usadas na avaliação de integrais duplas, como veremos mais adiante. Nós nos tornaremos hábeis no uso dessas propriedades assim que nos familiarizarmos com as ferramentas computacionais de integrais duplas. Então, vamos falar sobre isso agora.
Integrais iterados
Até agora, vimos como configurar uma integral dupla e como obter um valor aproximado para ela. Também podemos imaginar que avaliar integrais duplos usando a definição pode ser um processo muito demorado se escolhermos valores maiores para\(m\)\(n\) e. Portanto, precisamos de uma técnica prática e conveniente para calcular integrais duplos. Em outras palavras, precisamos aprender a calcular integrais duplos sem empregar a definição que usa limites e somas duplas.
A ideia básica é que a avaliação se torne mais fácil se pudermos dividir uma integral dupla em integrais simples, integrando primeiro em relação a uma variável e depois em relação à outra. A principal ferramenta de que precisamos é chamada de integral iterada.
Suponha que\(a\)\(b\)\(c\),, e\(d\) sejam números reais. Definimos uma integral iterada para uma função\(f(x,y)\) sobre a região retangular\(R =[a,b]×[c,d]\) como
\[\int_a^b\int_c^d f(x,y)\,dy \, dx = \int_a^b \left[\int_c^d f(x,y)\,dy \right] dx \nonumber \]
ou
\[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d \left[\int_a^b f(x,y)\,dx \right] dy. \nonumber \]
A notação\(\int_a^b \left[\int_c^d f(x,y)\,dy \right] dx\) significa que nos integramos em\(f(x,y)\) relação a\(y\) enquanto mantemos\(x\) constante. Da mesma forma, a notação\(\int_c^d \left[\int_a^b f(x,y)\,dx \right] dy\) significa que nos integramos em\(f(x,y)\) relação a\(x\) enquanto mantemos\(y\) constante. O fato de integrais duplos poderem ser divididos em integrais iterados é expresso no teorema de Fubini. Pense nesse teorema como uma ferramenta essencial para avaliar integrais duplos.
Suponha que\(f(x,y)\) seja uma função de duas variáveis que seja contínua em uma região retangular\(R = \big\{(x,y) ∈ \mathbb{R}^2 | \, a \leq x \leq b, \, c \leq y \leq d \big\}\). Então vemos na Figura\(\PageIndex{6}\) que a integral dupla de\(f\) sobre a região é igual a uma integral iterada,
\[\iint_R f(x,y)\,dA = \iint_R f(x,y)\,dx \, dy = \int_a^b \int_c^d f(x,y)\,dy \, dx = \int_c^d \int_a^b f(x,y)\,dx \, dy. \nonumber \]
De forma mais geral, o teorema de Fubini\(f\) é verdadeiro se for limitado\(R\) e\(f\) for descontínuo somente em um número finito de curvas contínuas. Em outras palavras,\(f\) tem que ser integrável\(R\).
Use o teorema de Fubini para calcular a integral dupla\(\displaystyle \iint_R f(x,y) \,dA\) onde\(f(x,y) = x\)\(R = [0, 2] \times [0, 1]\) e.
Solução
O teorema de Fubini oferece uma maneira mais fácil de calcular a integral dupla pelo uso de uma integral iterada. Observe como os valores de limite da região\(R\) se tornam os limites superior e inferior da integração.
\ [\ begin {align*}\ iint_R f (x, y)\, dA &=\ Iint_r f (x, y)\, dx\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {x=0} ^ {x=2} x\, dx\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1}\ left [\ frac {x^2} {2}\ bigg|_ {x=0} ^ {x=2}\ direita]\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1} 2\, dy = 2y\ bigg|_ {y=0 } ^ {y=1} = 2\ end {align*}\]
A integração dupla neste exemplo é simples o suficiente para usar o teorema de Fubini diretamente, permitindo converter uma integral dupla em uma integral iterada. Consequentemente, agora estamos prontos para converter todas as integrais duplas em integrais iteradas e demonstrar como as propriedades listadas anteriormente podem nos ajudar a avaliar integrais duplas quando a função\(f(x,y)\) é mais complexa. Observe que a ordem da integração pode ser alterada (consulte o Exemplo 7).
Avalie a integral dupla\[\iint_R (xy - 3xy^2) \,dA, \, \text{where} \, R = \big\{(x,y) \,| \, 0 \leq x \leq 2, \, 1 \leq y \leq 2 \big\}.\nonumber \]
Solução
Essa função tem duas partes: uma peça é\(xy\) e a outra é\(3xy^2\). Além disso, a segunda peça tem uma constante 3. Observe como usamos as propriedades i e ii para ajudar a avaliar a integral dupla.
\ [\ begin {align*}\ Iint_R (xy - 3xy^2)\, dA &=\ Iint_R xy\, dA +\ Iint_R (-3xy^2)\, dA & &\ text {Propriedade i: A integral de uma soma é a soma das integrais.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2} int_ {x=0} ^ {x=2} xy\, dx\, dy -\ int_ {y=1} ^ {y=2}\ int_ {x=0} ^ {x=2} 3xy^2\, dx\, dy & &\ texto {Converta integrais duplos em integrais iterados.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2}\ left (\ frac {x^2} {2} y\ right)\ bigg|_ {x=0} ^ {x=2}\, dy - 3\ int_ {y=1} ^ {y=2}\ left (\ frac {y=1} ^ {y=2}\ left (\ frac {x^2} {2} y^2\ right)\ bigg|_ {x=0} ^ {x=2}\, dy & &\ text {Integre em relação a $ x $, mantendo $ y $ constante.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2} 2y\, dy -\ int_ {y=1} ^ {y=2} 6y^2 dy & &\ text {Propriedade ii: Colocando a constante antes da integral.}\\ [4pt]
&= 2\ int_1^2 y\, dy - 6\ int_1^2 y^2\, dy & &\ text {Integre em relação a y.}\\ [4pt]
&= 2\ frac {y^2} {2}\ bigg|_1^2 - 6\ frac {y^3} {3}\ bigg|_1^2\\ [4pt]
&=y^2\ bigg|_1^2 - 2y^3\ bigg|_1^2\\ [4pt]
& =( 4−1) − 2 (8−1) = 3 − 2 (7) = 3 − 14 = −11. \ end {align*}\]
Sobre a região\(R = \big\{(x,y)\,| \, 1 \leq x \leq 3, \, 1 \leq y \leq 2 \big\}\), nós temos\(2 \leq x^2 + y^2 \leq 13\). Encontre um limite inferior e um limite superior para a integral\(\displaystyle \iint_R (x^2 + y^2)\,dA.\)
Solução
Para um limite inferior, integre a função constante 2 sobre a região\(R\). Para um limite superior, integre a função constante 13 sobre a região\(R\).
\[\begin{align*} \int_1^2 \int_1^3 2 \,dx \, dy &= \int_1^2 [2x\bigg|_1^3] \,dy = \int_1^2 2(2)dy = 4y\bigg|_1^2 = 4(2 - 1) = 4 \\[4pt] \int_1^2 \int_1^3 13dx \, dy &= \int_1^2 [13x\bigg|_1^3] \,dy = \int_1^2 13(2)\,dy = 26y\bigg|_1^2 = 26(2 - 1) = 26. \end{align*}\]
Conseqüentemente, obtemos\(\displaystyle 4 \leq \iint_R (x^2 + y^2) \,dA \leq 26.\)
Avalie\(\displaystyle \iint_R e^y \cos x \, dA\) a integral na região\(R = \big\{(x,y)\,| \, 0 \leq x \leq \frac{\pi}{2}, \, 0 \leq y \leq 1 \big\}\).
Solução
Esse é um ótimo exemplo para a propriedade vi porque a função\(f(x,y)\) é claramente o produto de duas funções de variável única\(e^y\)\(\cos x\) e. Assim, podemos dividir a integral em duas partes e, em seguida, integrar cada uma como um problema de integração de variável única.
\ [\ begin {align*}\ iint_R e^y\ cos x\, dA &=\ int_0^1\ int_0^ {\ pi/2} e^y\ cos x\, dx\, dy\\ [4pt]
&=\ left (\ int_0^1 e^y dy\ right)\ left (\ int_0^ {\ pi/2}\ cos x\, dx\ right)\\ [4pt]
&= (e^y\ bigg|_0^1) (\ sin x\ bigg|_0^ {\ pi/2})\\ [4pt]
&= e - 1. \ end {align*}\]
a. Use as propriedades da integral dupla e do teorema de Fubini para calcular a integral
\[\int_0^1 \int_{-1}^3 (3 - x + 4y) \,dy \, dx. \nonumber \]
b. Mostre\(\displaystyle 0 \leq \iint_R \sin \pi x \, \cos \pi y \, dA \leq \frac{1}{32}\) onde\(R = \left(0, \frac{1}{4}\right)\left(\frac{1}{4}, \frac{1}{2}\right)\).
- Dica
-
Use as propriedades i. e ii. e avalie a integral iterada e, em seguida, use a propriedade v.
- Responda
-
uma.\(26\)
b. As respostas podem variar.
Como mencionamos anteriormente, quando estamos usando coordenadas retangulares, a integral dupla sobre uma região\(R\) indicada por\(\iint_R f(x,y) \, dA\) pode ser escrita como\(\iint_R\, f(x,y) \, dx \, dy\) ou\(\iint_R \, f(x,y) \,dy \, dx.\) O próximo exemplo mostra que os resultados são os mesmos, independentemente da ordem de integração escolhida.
Vamos retornar à função\(f(x,y) = 3x^2 - y\) do Exemplo 1, desta vez na região retangular\(R = [0,2] \times [0,3]\). Use o teorema de Fubini para avaliar\(\iint_R f(x,y) \,dA\) de duas maneiras diferentes:
- Primeiro, integre com relação a\(y\) e depois com relação a\(x\);
- Primeiro, integre com relação a\(x\) e depois com relação\(y\) a.
Solução
A figura\(\PageIndex{6}\) mostra como o cálculo funciona de duas maneiras diferentes.
- Primeiro, integre com relação a\(y\) e, em seguida, integre com relação a\(x\):
\ [\ begin {align*}\ iint_R f (x, y)\, dA &=\ int_ {x=0} ^ {x=2}\ int_ {y=0} ^ {y=3} (3x^2 - y)\, dy\, dx\\ [4pt]
&=\ int_ {x=0} ^ {x=2}\ left (\ int_ {y=0} ^ {y=3} (3x^2 - y)\, dy\ direita)\, dx =\ int_ {x=0} ^ {x=2}\ esquerda [3x^2y -\ frac {y^2} {2}\ bigg|_ {y=0} ^ {y=3}\ direita]\, dx\\ [4pt]
&=\ int_ {x=0} ^ {x=2}\ esquerda (9x^2 -\ frac {9} {2}\ direita)\, dx = 3x^3 -\ frac {9} {2} x\ bigg|_ {x=0} ^ {x=2} = 15. \ end {align*}\]
- Primeiro\(x\) integre com relação a\(y\):
\ [\ begin {align*}\ iint_R f (x, y)\, dA &=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ left (\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\ right)\, dy \\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ left [x^3 - xy\ bigg|_ {x=0} ^ {x=2}\ direita] dy\\ [4pt]
&=\ int_ {y=0} ^ {y=3} (8 - 2y)\, dy = 8y - y^2\ bigg|_ {y=3} (8 - 2y)\, dy = 8y - y^2\ bigg|_ {y=3} =0} ^ {y=3} = 15. \ end {align*}\]
Análise
Com qualquer ordem de integração, a integral dupla nos dá uma resposta de\(15\). Talvez queiramos interpretar essa resposta como um volume em unidades cúbicas do sólido\(S\) abaixo da função\(f(x,y) = 3x^2 - y\) sobre a região\(R = [0,2] \times [0,3]\). No entanto, lembre-se de que a interpretação de uma integral dupla como um volume (sem sinal) funciona somente quando o integrando\(f\) é uma função não negativa sobre a região base\(R\).
Avalie
\[\int_{y=-3}^{y=2} \int_{x=3}^{x=5} (2 - 3x^2 + y^2) \,dx \, dy. \nonumber \]
- Dica
-
Use o teorema de Fubini.
- Responda
-
\(-\frac{1340}{3}\)
No exemplo a seguir, vemos que, na verdade, pode ser benéfico mudar a ordem da integração para facilitar a computação. Voltaremos a essa ideia várias vezes neste capítulo.
Considere a integral dupla\(\displaystyle \iint_R x \, \sin (xy) \, dA\) sobre a região\(R = \big\{(x,y) \,| \, 0 \leq x \leq \pi, \, 1 \leq y \leq 2 \big\}\) (Figura\(\PageIndex{7}\)).
- Expresse a integral dupla de duas maneiras diferentes.
- Analise se avaliar a integral dupla de uma forma é mais fácil do que a outra e por quê.
- Avalie a integral.
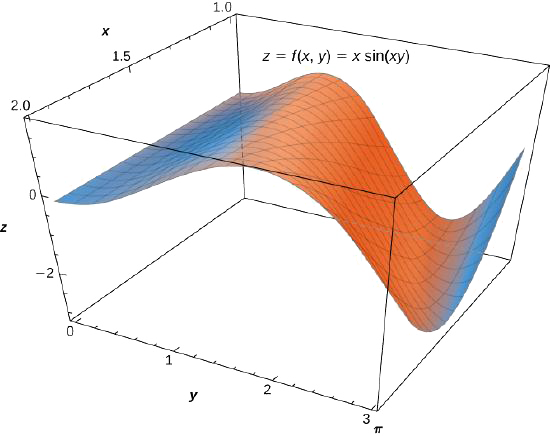
- Podemos\(\iint_R x \, \sin (xy) \,dA\) nos expressar das duas maneiras a seguir: primeiro integrando com relação a\(y\) e depois com relação a\(x\); segundo, integrando com relação a\(x\) e depois com relação\(y\) a.
\[\iint_R x \, \sin (xy) \,dA= \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \,dy \, dx \nonumber \]
Integre primeiro em relação\(y\) a.
\[= \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \, \sin (xy) \,dx \, dy \nonumber \]
Integre primeiro em relação\(x\) a. - Se quisermos integrar em relação a y primeiro e depois integrar com relação a\(x\), vemos que podemos usar a substituição\(u = xy\), que dá\(du = x \, dy\). Portanto, a integral interna é simples\(\int \sin u \, du\) e podemos mudar os limites para serem funções de\(x\),
\[\iint_R x \, \sin (xy) \,dA = \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \, dy \, dx = \int_{x=0}^{x=\pi} \left[\int_{u=x}^{u=2x} \sin (u) \,du \right] \, dx.\nonumber \]
No entanto, integrar em relação\(x\) primeiro e depois integrar em relação a\(y\) requer integração por partes para a integral interna, com\(u = x\) e\(dv = \sin(xy)dx\)
Então\(du = dx\) e\(v = - \frac{\cos(xy)}{y}\), então
\[\iint_R x \sin(xy) \,dA = \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \sin(xy) \,dx \, dy = \int_{y=1}^{y=2} \left[ - \frac{x \, \cos (xy)}{y} \bigg|_{x=0}^{x=\pi} + \frac{1}{y} \int_{x=0}^{x=\pi} \cos(xy)\,dx \right] \, dy.\nonumber \]
Como a avaliação está ficando complicada, só faremos o cálculo mais fácil de fazer, que é claramente o primeiro método.
- Avalie a integral dupla usando a maneira mais fácil.
\ [\ begin {align*}\ iint_R x\,\ sin (xy)\, dA &=\ int_ {x=0} ^ {x=\ pi}\ int_ {y=1} ^ {y=2} x\,\ sin (xy)\, dy\, dx\\ [4pt]
&=\ int_ {x=0} ^ {x=\ pi} esquerda [\ int_ {u=x} ^ {u=2x}\ sin (u)\, du\ right]\, dx =\ int_ {x=0} ^ {x=\ pi}\ esquerda [-\ cos u\ bigg|_ {u=x} ^ {u=2x}\ direita]\, dx\\ [4pt]
&=\ int _ {x=0} ^ {x=\ pi} (-\ cos 2x +\ cos x)\, dx\\ [4pt]
&=\ left (-\ frac {1} {2}\ sin 2x +\ sin x\ direita)\ bigg|_ {x=0} ^ {x=\ pi} = 0. \ end {align*}\]
Avalie a integral\(\displaystyle \iint_R xe^{xy}\,dA\) onde\(R = [0,1] \times [0, \ln 5]\).
- Dica
-
Integre com relação ao\(y\) primeiro.
- Responda
-
\(\frac{4 - \ln 5}{\ln 5}\)
Aplicações de integrais duplos
Integrais duplos são muito úteis para encontrar a área de uma região delimitada por curvas de funções. Descreveremos essa situação com mais detalhes na próxima seção. No entanto, se a região tiver uma forma retangular, podemos encontrar sua área integrando a função constante\(f(x,y) = 1\) sobre a região\(R\).
A área da região\(R\) é dada por\[A(R) = \iint_R 1 \, dA. \nonumber \]
Essa definição faz sentido porque usar\(f(x,y) = 1\) e avaliar a integral a tornam um produto de comprimento e largura. Vamos verificar essa fórmula com um exemplo e ver como isso funciona.
Encontre a área da região\(R = \big\{\,(x,y)\,|\,0 \leq x \leq 3, \, 0 \leq y \leq 2\big\}\) usando uma integral dupla, ou seja, integrando-se\(1\) sobre a região\(R\).
Solução
A região é retangular com comprimento\(3\) e largura\(2\), então sabemos que a área é\(6\). Recebemos a mesma resposta quando usamos uma integral dupla:
\[A(R) = \int_0^2 \int_0^3 1 \, dx \, dy = \int_0^2 \left[x\big|_0^3\right] \, dy = \int_0^2 3 dy = 3 \int_0^2 dy = 3y\bigg|_0^2 = 3(2) = 6 \, \text{units}^2.\nonumber \]
Já vimos como integrais duplas podem ser usadas para encontrar o volume de um sólido limitado acima por uma função\(f(x,y) \geq 0\) sobre uma região\(R\) fornecida\(f(x,y) \geq 0\) para all\((x,y)\) in\(R\). Aqui está outro exemplo para ilustrar esse conceito.
Encontre o volume\(V\) do sólido\(S\) que é limitado pelo parabolóide elíptico\(2x^2 + y^2 + z = 27\), os planos\(x = 3\) e\(y = 3\) e os três planos coordenados.
Solução
Primeiro observe o gráfico da superfície\(z = 27 - 2x^2 - y^2\) na Figura\(\PageIndex{8}\) (a) e acima da região quadrada\(R_1 = [-3,3] \times [-3,3]\). No entanto, precisamos do volume do sólido limitado pelo parabolóide elíptico\(2x^2 + y^2 + z = 27\), pelos planos\(x = 3\) e\(y = 3\) e pelos três planos coordenados.
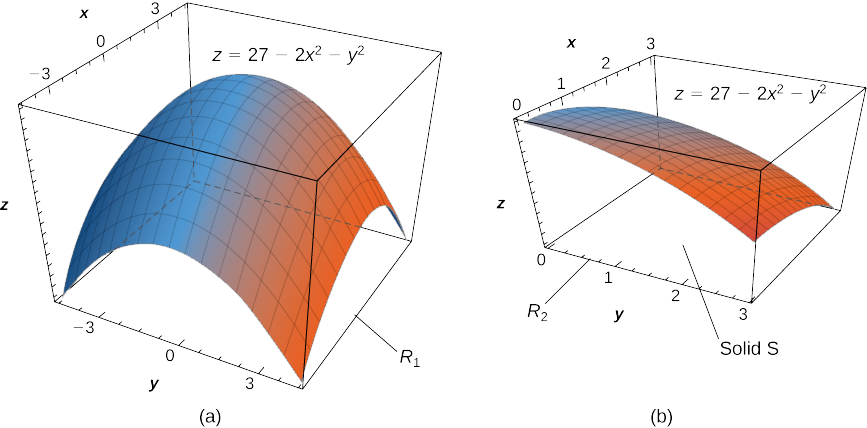
Agora vamos ver o gráfico da superfície na Figura\(\PageIndex{8}\) (b). Determinamos o volume\(V\) avaliando a integral dupla sobre\(R_2\):
\ [\ begin {align*} V &=\ Iint_R z\, dA =\ Iint_R (27 - 2x^2 - y^2)\, dA\\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x=3} (27 - 2x^2 - y^2)\, dx\, dy & &\ text {Converter em integral literal.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} [27x -\ frac {2} {3} x^3 - y^2x]\ bigg|_ {x=0} ^ {x=3}\ , dy & &\ text {Integre em relação a $x$.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} (63 - 3y^2) dy = 63 y - y^3\ bigg|_ {y=0} ^ {y=3} = 162. \ end {align*}\]
Encontre o volume do sólido delimitado acima pelo gráfico de\(f(x,y) = xy \sin(x^2y)\) e abaixo pelo\(xy\) plano -na região retangular\(R = [0,1] \times [0,\pi]\).
- Dica
-
Faça um gráfico da função, configure a integral e use uma integral iterada.
- Responda
-
\(\frac{\pi}{2}\)
Lembre-se de que definimos o valor médio de uma função de uma variável em um intervalo\([a,b]\) como
\[f_{ave} = \frac{1}{b - a} \int_a^b f(x) \, dx. \nonumber \]
Da mesma forma, podemos definir o valor médio de uma função de duas variáveis em uma região \(R\). A principal diferença é que dividimos por uma área em vez da largura de um intervalo.
O valor médio de uma função de duas variáveis em uma região\(R\) é
\[F_{ave} = \frac{1}{\text{Area of} \, R} \iint_R f(x,y)\, dx \, dy. \nonumber \]
No próximo exemplo, encontramos o valor médio de uma função sobre uma região retangular. Esse é um bom exemplo de como obter informações úteis para uma integração fazendo medições individuais em uma grade, em vez de tentar encontrar uma expressão algébrica para uma função.
O mapa meteorológico na Figura\(\PageIndex{9}\) mostra um sistema de tempestades invulgarmente úmido associado aos restos do furacão Karl, que despejou 4—8 polegadas (100-200 mm) de chuva em algumas partes do Centro-Oeste de 22 a 23 de setembro de 2010. A área de precipitação mediu 300 milhas de leste a oeste e 250 milhas de norte a sul. Estime a precipitação média em toda a área nesses dois dias.
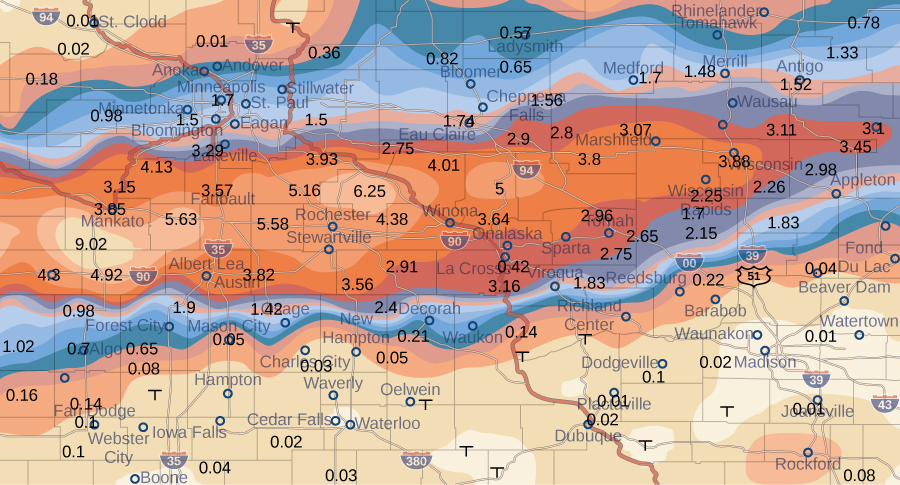
Solução
Coloque a origem no canto sudoeste do mapa para que todos os valores possam ser considerados como estando no primeiro quadrante e, portanto, todos sejam positivos. Agora divida o mapa inteiro em seis retângulos\((m = 2\) e\(n = 3)\), conforme mostrado na Figura\(\PageIndex{9}\). Suponha que\(f(x,y)\) denota a precipitação da tempestade em polegadas em um ponto aproximadamente\(x\) milhas a leste da origem e\(y\) milhas ao norte da origem. Vamos\(R\) representar toda a área de milhas\(250 \times 300 = 75000\) quadradas. Então, a área de cada sub-retângulo é
\[\Delta A = \frac{1}{6} (75000) = 12500.\nonumber \]
Suponha que\((x_{ij}*,y_{ij}*)\) sejam aproximadamente os pontos médios de cada sub-retângulo\(R_{ij}\). Observe a região codificada por cores em cada um desses pontos e estime a precipitação. A precipitação em cada um desses pontos pode ser estimada como:
- Em (\(x_{11}, y_{11}\)), a pluviosidade é de 0,08.
- Em (\(x_{12}, y_{12}\)), a pluviosidade é de 0,08.
- Em (\(x_{13}, y_{13}\)), a pluviosidade é de 0,01.
- Em (\(x_{21}, y_{21}\)), a pluviosidade é de 1,70.
- Em (\(x_{22}, y_{22}\)), a pluviosidade é de 1,74.
- Em (\(x_{23}, y_{23}\)), a pluviosidade é de 3.00.
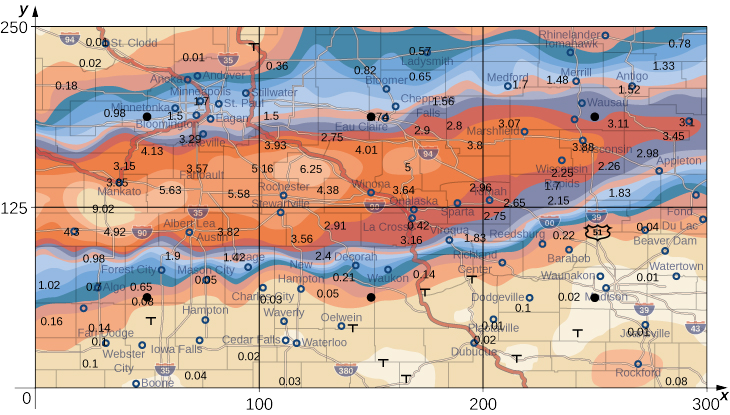
De acordo com nossa definição, a precipitação média de tempestade em toda a área durante esses dois dias foi
\ [\ begin {align*} f_ {ave} =\ frac {1} {Área\, R}\ Iint_r f (x, y)\, dx\, dy &=\ frac {1} {75000}\ Iint_r f (x, y)\, dx\, dy\\ [4pt]
&\ approx\ frac {1} {75000} sum_ {i=1} ^3\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Delta A\\ [4pt]
&=\ frac {1} {75000}\ Bigg [f (x_ {11} ^*, y_ {11} ^*)\ Delta A + f (x_ {12} ^*, y_ {12} ^*)\ Delta A + f (x_ {13} ^*, y_ {13} ^*)\ Delta A + f (x_ {21} ^*, y_ {21} ^*)\ Delta A + f (x_ {22} ^*, y_ {22} ^*)\ Delta A + f (x_ {22} ^*)\ Delta A + f (x_ {22} ^*)\ Delta A + f (x_ {22} ^*)\ Delta A + f (x_ {22} ^*} ^*, y_ {23} ^*)\ Delta A\ Bigg]\\ [4 pontos]
&\ approx\ frac {1} {75000}\ Grande [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Grande]\ Delta A\\ [4 pontos]
&=\ frac {1} {75000}\ Grande [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Grande] 12500\\ [4 pontos]
&=\ frac {1} {6}\ Grande [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Grande]\\[4pt] &\approx 1.10 \;\text{in}. \end{align*}\]
De 22 a 23 de setembro de 2010, essa área teve uma precipitação média de tempestade de aproximadamente 1,10 polegadas.
Um mapa de contorno é exibido para uma função\(f(x,y)\) no retângulo\(R = [-3,6] \times [-1, 4]\).
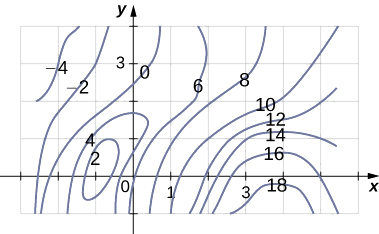
a. Use a regra do ponto médio com\(m = 3\) e\(n = 2\) para estimar o valor de\(\displaystyle \iint_R f(x,y) \,dA.\)
b. Estime o valor médio da função\(f(x,y)\).
- Dica
-
Divida a região em seis retângulos e use as linhas de contorno para estimar os valores de\(f(x,y)\).
- Responda
-
As respostas para ambas as partes a. e b. podem variar.
Conceitos-chave
- Podemos usar uma soma dupla de Riemann para aproximar o volume de um sólido limitado acima por uma função de duas variáveis em uma região retangular. Ao tomar o limite, isso se torna uma integral dupla representando o volume do sólido.
- As propriedades da integral dupla são úteis para simplificar a computação e encontrar limites em seus valores.
- Podemos usar o teorema de Fubini para escrever e calcular uma integral dupla como uma integral iterada.
- Integrais duplas são usadas para calcular a área de uma região, o volume sob uma superfície e o valor médio de uma função de duas variáveis sobre uma região retangular.
Equações-chave
- \[\iint_R f(x,y) \,dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(x_ij*,y_ij*)\,ΔA\nonumber \]
- \[\int_a^b \int_c^d f(x,y)\,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \,dy \right] dx\nonumber \]ou
\[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d\left[ \int_a^b f(x,y) \,dx \right] dy\nonumber \]
- \[f_{ave} = \frac{1}{\text{Area of}\, R} \iint_R f(x,y) \,dx \, dy\nonumber \]
Glossário
- integral duplo
- da função\(f(x,y)\) sobre a região\(R\) no\(xy\) plano -é definido como o limite de uma soma dupla de Riemann,
- \[ \iint_R f(x,y) \,dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A.\nonumber \]
- soma dupla de Riemann
- da função\(f(x,y)\) sobre uma região retangular\(R\) é
- \[\sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A,\nonumber \]
- onde\(R\) é dividido em sub-retângulos menores\(R_{ij}\) e\((x_{ij}^*, y_{ij}^*)\) é um ponto arbitrário em\(R_{ij}\)
- Teorema de Fubini
- se\(f(x,y)\) é uma função de duas variáveis que é contínua sobre uma região retangular\(R = \big\{(x,y) \in \mathbb{R}^2 \,|\,a \leq x \leq b, \, c \leq y \leq d\big\}\), então a integral dupla de\(f\) sobre a região é igual a uma integral iterada,
- \[\displaystyle\iint_R f(x,y) \, dA = \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_c^d \int_a^b f(x,y) \,dx \, dy\nonumber \]
- integral iterado
- para uma função\(f(x,y)\) na região\(R\) é
uma.\(\displaystyle \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \, dy\right] \, dx,\)
b.\(\displaystyle \int_c^d \int_a^b f(x,y) \, dx \, dy = \int_c^d \left[\int_a^b f(x,y) \, dx\right] \, dy,\)
onde\(a,b,c\) e\(d\) são quaisquer números reais e\(R = [a,b] \times [c,d]\)


