Skip to main content
Global

15.1E: Exercícios para a Seção 15.1

  1. Last updated
  2. Save as PDF
  • Page ID
    188062

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 e 2, use a regra do ponto médio com\(m = 4\) e\(n = 2\) para estimar o volume do sólido limitado pela superfície\(z = f(x,y)\), os planos verticais\(x = 1\)\(x = 2\)\(y = 1\),\(y = 2\), e e o plano horizontal\(x = 0\).

    1)\(f(x,y) = 4x + 2y + 8xy\)

    Resposta
    \(27\)

    2)\(f(x,y) = 16x^2 + \frac{y}{2}\)

    Nos exercícios 3 e 4, estime o volume do sólido sob a superfície\(z = f(x,y)\) e acima da região retangular R usando uma soma de Riemann com\(m = n = 2\) e os pontos de amostra como sendo os cantos inferiores esquerdos dos sub-retângulos da partição.

    3)\(f(x,y) = \sin x - \cos y\),\(R = [0, \pi] \times [0, \pi]\)

    Resposta
    \(0\)

    4)\(f(x,y) = \cos x + \cos y\),\(R = [0, \pi] \times [0, \frac{\pi}{2}]\)

    5) Use a regra do ponto médio com\(m = n = 2\) para estimar\(\iint_R f(x,y) \,dA\), onde os valores da função f on\(R = [8,10] \times [9,11]\) são fornecidos na tabela a seguir.

    \(y\)
    \(x\) \ (y\) ">9 9.5 10 10,5 11
    8 \ (y\) ">9,8 5 6.7 5 5.6
    8.5 \ (y\) ">9,4 4.5 8 5.4 3.4
    9 \ (y\) ">8,7 4.6 6 5.5 3.4
    9.5 \ (y\) ">6,7 6 4.5 5.4 6.7
    10 \ (y\) ">6,8 6.4 5.5 5.7 6.8
    Resposta
    \(21.3\)

    6) Os valores da função\(f\) no retângulo\(R = [0,2] \times [7,9]\) são fornecidos na tabela a seguir. Estime a integral dupla\(\iint_R f(x,y)\,dA\) usando uma soma de Riemann com\(m = n = 2\). Selecione os pontos de amostra para serem os cantos superiores direitos dos subquadrados de R.

    \(y_0 = 7\) \(y_1 = 8\) \(y_2 = 9\)
    \(x_0 = 0\) \ (y_0 = 7\) ">10,22 \ (y_1 = 8\) ">10,21 \ (y_2 = 9\) ">9,85
    \(x_1 = 1\) \ (y_0 = 7\) ">6,73 \ (y_1 = 8\) ">9,75 \ (y_2 = 9\) ">9,63
    \(x_2 = 2\) \ (y_0 = 7\) ">5,62 \ (y_1 = 8\) ">7,83 \ (y_2 = 9\) ">8,21

    7) A profundidade de uma piscina infantil de 4 pés por 4 pés, medida em intervalos de 1 pé, é dada na tabela a seguir.

    1. Estime o volume de água na piscina usando uma soma de Riemann com\(m = n = 2\). Selecione os pontos de amostra usando a regra do ponto médio ativada\(R = [0,4] \times [0,4]\).
    2. Encontre a profundidade média da piscina.
      \(y\)
      \(x\) \ (y\) ">0 1 2 3 4
      0 \ (y\) ">1 1,5 2 2,5 3
      1 \ (y\) ">1 1,5 2 2,5 3
      2 \ (y\) ">1 1,5 1,5 2,5 3
      3 \ (y\) ">1 1 1,5 2 2,5
      4 \ (y\) ">1 1 1 1,5 2
    Resposta
    a. 28\(\text{ft}^3\)
    b. 1,75 pés

    8) A profundidade de um furo de 3 pés por 3 pés no solo, medida em intervalos de 1 pé, é dada na tabela a seguir.

    1. Estime o volume do furo usando uma soma de Riemann com\(m = n = 3\) e os pontos de amostra como sendo os cantos superiores esquerdos dos subquadrados de \(R\).
    2. Encontre a profundidade média do furo.
      \(y\)
      \(x\) \ (y\) ">0 1 2 3
      0 \ (y\) ">6 6.5 6.4 6
      1 \ (y\) ">6,5 7 7.5 6.5
      2 \ (y\) ">6,5 6.7 6.5 6
      3 \ (y\) ">6 6.5 5 5.6

    9) As curvas\(f(x,y) = k\) de nível da função\(f\) são dadas no gráfico a seguir, onde\(k\) é uma constante.

    1. Aplique a regra do ponto médio com\(m = n = 2\) para estimar a integral dupla\(\iint_R f(x,y)\,dA\), onde\(R = [0.2,1] \times [0,0.8]\).
    2. Estime o valor médio da função\(f\) ativada\(R\).

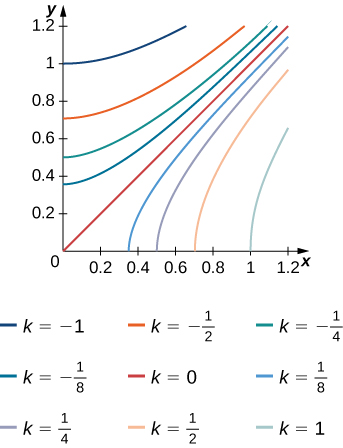
    Resposta
    a. 0,112
    b.\(f_{ave} ≃ 0.175\); aqui\(f(0.4,0.2) ≃ 0.1\),\(f(0.2,0.6) ≃− 0.2\)\(f(0.8,0.2) ≃ 0.6\), e\(f(0.8,0.6) ≃ 0.2\)

    10) As curvas\(f(x,y) = k\) de nível da função\(f\) são dadas no gráfico a seguir, onde\(k\) é uma constante.

    1. Aplique a regra do ponto médio com\(m = n = 2\) para estimar a integral dupla\(\iint_R f(x,y)\,dA\), onde\(R = [0.1,0.5] \times [0.1,0.5]\).
    2. Estime o valor médio da função f on\(R\).

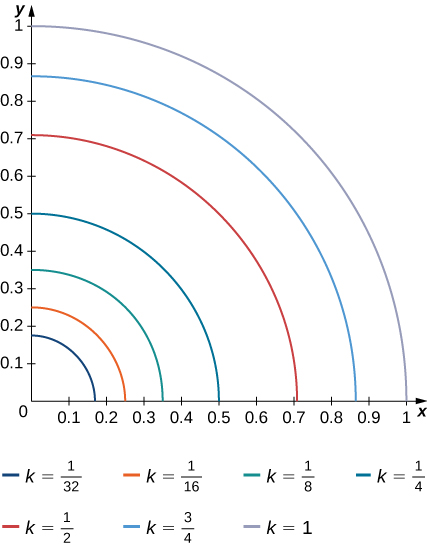
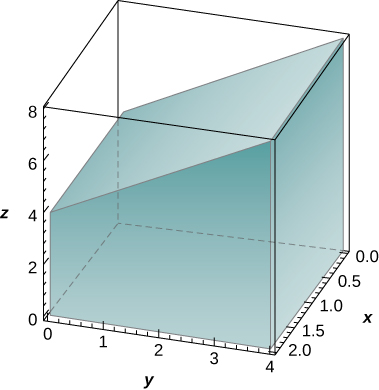
    11) O sólido que está sob a superfície\(z = \sqrt{4 - y^2}\) e acima da região retangular\( R = [0,2] \times [0,2]\) é ilustrado no gráfico a seguir. Calcule a integral dupla\(\iint_Rf(x,y)\), onde\(f(x,y) = \sqrt{4 - y^2}\) encontra o volume do sólido correspondente.

    Resposta
    \(2\pi\)

    12) O sólido que está abaixo do plano\(z = y + 4\) e acima da região retangular\(R = [0,2] \times [0,4]\) é ilustrado no gráfico a seguir. Calcule a integral dupla\(\iint_R f(x,y)\,dA\)\(f(x,y) = y + 4\), onde, encontrando o volume do sólido correspondente.

    Nos exercícios 13 a 20, calcule as integrais invertendo a ordem de integração.

    13)\(\displaystyle \int_{-1}^1\left(\int_{-2}^2 (2x + 3y + 5)\,dx \right) \space dy\)

    Resposta
    \(40\)

    14)\(\displaystyle \int_0^2\left(\int_0^1 (x + 2e^y + 3)\,dx \right) \space dy\)

    15)\(\displaystyle \int_1^{27}\left(\int_1^2 (\sqrt[3]{x} + \sqrt[3]{y})\,dy \right) \space dx\)

    Resposta
    \(\frac{81}{2} + 39\sqrt[3]{2}\)

    16)\(\displaystyle \int_1^{16}\left(\int_1^8 (\sqrt[4]{x} + 2\sqrt[3]{y})\,dy \right) \space dx\)

    17)\(\displaystyle \int_{\ln 2}^{\ln 3}\left(\int_0^1 e^{x+y}\,dy \right) \space dx\)

    Resposta
    \(e - 1\)

    18)\(\displaystyle \int_0^2\left(\int_0^1 3^{x+y}\,dy \right) \space dx\)

    19)\(\displaystyle \int_1^6\left(\int_2^9 \frac{\sqrt{y}}{x^2}\,dy \right) \space dx\)

    Resposta
    \(15 - \frac{10\sqrt{2}}{9}\)

    20)\(\displaystyle \int_1^9 \left(\int_4^2 \frac{\sqrt{x}}{y^2}\,dy \right)\,dx\)

    Nos exercícios 21 a 34, avalie as integrais iteradas escolhendo a ordem de integração.

    21)\(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \sin(2x)\cos(3y)\,dx \space dy\)

    Resposta
    \(0\)

    22)\(\displaystyle \int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)]\,dx \space dy\)

    23)\(\displaystyle \int_1^e \int_1^e \left[\frac{1}{x}\sin(\ln x) + \frac{1}{y}\cos (\ln y)\right] \,dx \space dy\)

    Resposta
    \((e − 1)(1 + \sin 1 − \cos 1)\)

    24)\(\displaystyle \int_1^e \int_1^e \frac{\sin(\ln x)\cos (\ln y)}{xy} \,dx \space dy\)

    25)\(\displaystyle \int_1^2 \int_1^2 \left(\frac{\ln y}{x} + \frac{x}{2y + 1}\right)\,dy \space dx\)

    Resposta
    \(\frac{3}{4}\ln \left(\frac{5}{3}\right) + 2 (\ln 2)^2 - \ln 2\)

    26)\(\displaystyle \int_1^e \int_1^2 x^2 \ln(x)\,dy \space dx\)

    27)\(\displaystyle \int_1^{\sqrt{3}} \int_1^2 y \space \arctan \left(\frac{1}{x}\right) \,dy \space dx\)

    Resposta
    \(\frac{1}{8}[(2\sqrt{3} - 3) \pi + 6 \space \ln 2]\)

    28)\(\displaystyle \int_0^1 \int_0^{1/2} (\arcsin x + \arcsin y)\,dy \space dx\)

    29)\(\displaystyle \int_0^1 \int_1^2 xe^{x+4y}\,dy \space dx\)

    Resposta
    \(\frac{1}{4}e^4 (e^4 - 1)\)

    30)\(\displaystyle \int_1^2 \int_0^1 xe^{x-y}\,dy \space dx\)

    31)\(\displaystyle \int_1^e \int_1^e \left(\frac{\ln y}{\sqrt{y}} + \frac{\ln x}{\sqrt{x}}\right)\,dy \space dx\)

    Resposta
    \(4(e - 1)(2 - \sqrt{e})\)

    32)\(\displaystyle \int_1^e \int_1^e \left(\frac{x \space \ln y}{\sqrt{y}} + \frac{y \space \ln x}{\sqrt{x}}\right)\,dy \space dx\)

    33)\(\displaystyle \int_0^1 \int_1^2 \left(\frac{x}{x^2 + y^2} \right)\,dy \space dx\)

    Resposta
    \(-\frac{\pi}{4} + \ln \left(\frac{5}{4}\right) - \frac{1}{2} \ln 2 + \arctan 2\)

    34)\(\displaystyle \int_0^1 \int_1^2 \frac{y}{x + y^2}\,dy \space dx\)

    Nos exercícios 35 a 38, encontre o valor médio da função sobre os retângulos fornecidos.

    35)\(f(x,y) = −x +2y\),\(R = [0,1] \times [0,1]\)

    Resposta
    \(\frac{1}{2}\)

    36)\(f(x,y) = x^4 + 2y^3\),\(R = [1,2] \times [2,3]\)

    37)\(f(x,y) = \sinh x + \sinh y\),\(R = [0,1] \times [0,2]\)

    Resposta
    \(\frac{1}{2}(2 \space \cosh 1 + \cosh 2 - 3)\).

    38)\(f(x,y) = \arctan(xy)\),\(R = [0,1] \times [0,1]\)

    39) Seja\(f\) e\(g\) seja duas funções contínuas,\(0 \leq m_1 \leq f(x) \leq M_1\) para qualquer\(x ∈ [a,b]\) e\(0 \leq m_2 \leq g(y) \leq M_2\) para qualquer uma\( y ∈ [c,d]\). Mostre que a seguinte desigualdade é verdadeira:

    \[m_1m_2(b-a)(c-d) \leq \int_a^b \int_c^d f(x) g(y)\,dy dx \leq M_1M_2 (b-a)(c-d). \nonumber \]

    Nos exercícios 40 a 43, use a propriedade v. de integrais duplas e a resposta do exercício anterior para mostrar que as seguintes desigualdades são verdadeiras.

    40)\(\frac{1}{e^2} \leq \iint_R e^{-x^2 - y^2} \space dA \leq 1\), onde\(R = [0,1] \times [0,1]\)

    41)\(\frac{\pi^2}{144} \leq \iint_R \sin x \cos y \space dA \leq \frac{\pi^2}{48}\), onde\(R = \left[ \frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[ \frac{\pi}{6}, \frac{\pi}{3}\right]\)

    42)\(0 \leq \iint_R e^{-y}\space \cos x \space dA \leq \frac{\pi}{2}\), onde\(R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]\)

    43)\(0 \leq \iint_R (\ln x)(\ln y) \,dA \leq (e - 1)^2\), onde\(R = [1, e] \times [1, e] \)

    44) Seja\(f\) e\(g\) seja duas funções contínuas,\(0 \leq m_1 \leq f(x) \leq M_1\) para qualquer\(x ∈ [a,b]\) e\(0 \leq m_2 \leq g(y) \leq M_2\) para qualquer uma\(y ∈ [c,d]\). Mostre que a seguinte desigualdade é verdadeira:

    \[(m_1 + m_2) (b - a)(c - d) \leq \int_a^b \int_c^d |f(x) + g(y)| \space dy \space dx \leq (M_1 + M_2)(b - a)(c - d) \nonumber \]

    Nos exercícios 45 a 48, use a propriedade v. de integrais duplas e a resposta do exercício anterior para mostrar que as seguintes desigualdades são verdadeiras.

    45)\(\frac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) \,dA \leq 2\), onde\(R = [0,1] \times [0,1]\)

    46)\(\frac{\pi^2}{36}\iint_R (\sin x + \cos y)\,dA \leq \frac{\pi^2 \sqrt{3}}{36}\), onde\(R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]\)

    47)\(\frac{\pi}{2}e^{-\pi/2} \leq \iint_R (\cos x + e^{-y})\,dA \leq \pi\), onde\(R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]\)

    48)\(\frac{1}{e} \leq \iint_R (e^{-y} - \ln x) \,dA \leq 2\), onde\(R = [0, 1] \times [0, 1]\)

    Nos exercícios 49 a 50, a função\(f\) é dada em termos de integrais duplas.

    1. Determine a forma explícita da função\(f\).
    2. Encontre o volume do sólido abaixo da superfície\(z = f(x,y)\) e acima da região\(R\).
    3. Encontre o valor médio da função\(f\) em\(R\).
    4. Use um sistema computacional de álgebra (CAS) para traçar\(z = f(x,y)\) e\(z = f_{ave}\) no mesmo sistema de coordenadas.

    49) [T]\(f(x,y) = \int_0^y \int_0^x (xs + yt) ds \space dt\), onde\((x,y) \in R = [0,1] \times [0,1]\)

    Resposta

    a.\(f(x,y) = \frac{1}{2} xy (x^2 + y^2)\);
    b.\(V = \int_0^1 \int_0^1 f(x,y)\,dx \space dy = \frac{1}{8}\);
    c.\(f_{ave} = \frac{1}{8}\);

    d.

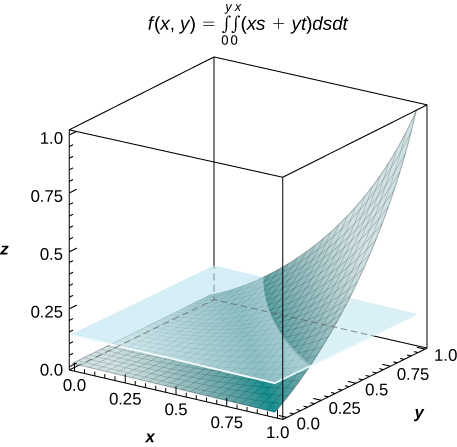
    50) [T]\(f(x,y) = \int_0^x \int_0^y [\cos(s) + \cos(t)] \, dt \space ds\), onde\((x,y) \in R = [0,3] \times [0,3]\)

    51) Mostre que se\(f\) e\(g\) são contínuos\([a,b]\) e\([c,d]\), respectivamente, então

    \(\displaystyle \int_a^b \int_c^d |f(x) + g(y)| dy \space dx = (d - c) \int_a^b f(x)\,dx\)

    \(\displaystyle + \int_a^b \int_c^d g(y)\,dy \space dx = (b - a) \int_c^d g(y)\,dy + \int_c^d \int_a^b f(x)\,dx \space dy\).

    52) Mostre isso\(\displaystyle \int_a^b \int_c^d yf(x) + xg(y)\,dy \space dx = \frac{1}{2} (d^2 - c^2) \left(\int_a^b f(x)\,dx\right) + \frac{1}{2} (b^2 - a^2) \left(\int_c^d g(y)\,dy\right)\).

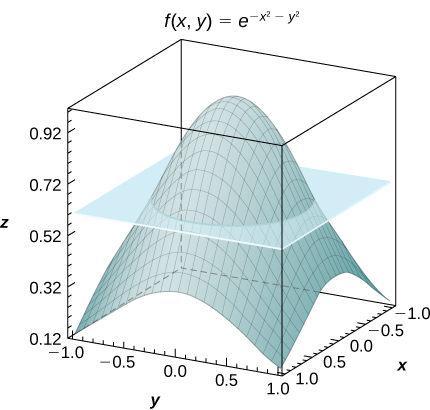
    53) [T] Considere a função\(f(x,y) = e^{-x^2-y^2}\), onde\((x,y) \in R = [−1,1] \times [−1,1]\).

    1. Use a regra do ponto médio com\(m = n = 2,4,..., 10\) para estimar a integral dupla\(I = \iint_R e^{-x^2 - y^2} dA\). Arredonde suas respostas para os centésimos mais próximos.
    2. Para\(m = n = 2\), encontre o valor médio de f sobre a região R. Arredonde sua resposta para os centésimos mais próximos.
    3. Use um CAS para representar graficamente no mesmo sistema de coordenadas o sólido cujo volume é dado por\(\iint_R e^{-x^2-y^2} dA\) e o plano\(z = f_{ave}\).
    Resposta

    a. Para\(m = n = 2\),\(I = 4e^{-0.5} \approx 2.43\)
    b.\(f_{ave} = e^{-0.5} \simeq 0.61\);

    c.

    54) [T] Considere a função\(f(x,y) = \sin (x^2) \space \cos (y^2)\), onde\((x,y \in R = [−1,1] \times [−1,1]\).

    1. Use a regra do ponto médio com\(m = n = 2,4,..., 10\) para estimar a integral dupla\(I = \iint_R \sin (x^2) \cos (y^2) \space dA\). Arredonde suas respostas para os centésimos mais próximos.
    2. Para\(m = n = 2\), encontre o valor médio de\(f\) mais da região R. Arredonde sua resposta para os centésimos mais próximos.
    3. Use um CAS para representar graficamente no mesmo sistema de coordenadas o sólido cujo volume é dado por\(\iint_R \sin(x^2) \cos(y^2) \space dA\) e o plano\(z = f_{ave}\).

    Nos exercícios 55 a 56, as funções\(f_n\) são dadas, onde\(n \geq 1\) está um número natural.

    1. Encontre o volume dos sólidos\(S_n\) sob as superfícies\(z = f_n(x,y)\) e acima da região\(R\).
    2. Determine o limite dos volumes dos sólidos à\(S_n\) medida que\(n\) aumenta sem limite.

    55)\(f(x,y) = x^n + y^n + xy, \space (x,y) \in R = [0,1] \times [0,1]\)

    Resposta
    a.\(\frac{2}{n + 1} + \frac{1}{4}\)
    b.\(\frac{1}{4}\)

    56)\(f(x,y) = \frac{1}{x^n} + \frac{1}{y^n}, \space (x,y) \in R = [1,2] \times [1,2]\)

    57) Mostre que o valor médio de uma função\(f\) em uma região retangular\(R = [a,b] \times [c,d]\) é\(f_{ave} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\), onde\((x_{ij}^*,y_{ij}^*)\) estão os pontos de amostra da partição de\(R\), onde\(1 \leq i \leq m\)\(1 \leq j \leq n\) e.

    58) Use a regra do ponto médio com\(m = n\) para mostrar que o valor médio de uma função\(f\) em uma região retangular\(R = [a,b] \times [c,d]\) é aproximado por

    \[f_{ave} \approx \frac{1}{n^2} \sum_{i,j =1}^n f \left(\frac{1}{2} (x_{i=1} + x_i), \space \frac{1}{2} (y_{j=1} + y_j)\right). \nonumber \]

    59) Um mapa isotérmico é um gráfico conectando pontos com a mesma temperatura em um determinado momento por um determinado período de tempo. Use o exercício anterior e aplique a regra do ponto médio com\(m = n = 2\) para encontrar a temperatura média na região dada na figura a seguir.

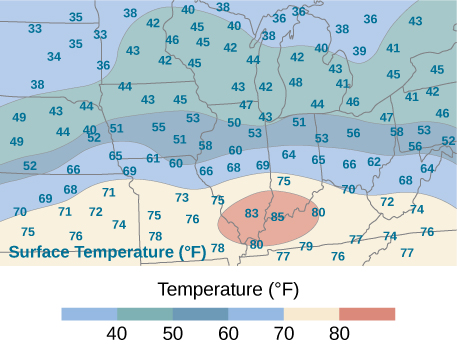
    Resposta
    \(56.5^{\circ}\)F; aqui\(f(x_1^*,y_1^*) = 71, \space f(x_2^*, y_1^*) = 72, \space f(x_2^*,y_1^*) = 40, \space f(x_2^*,y_2^*) = 43\), onde\(x_i^*\) e\(y_j^*\) são os pontos médios dos subintervalos das partições de\([a,b]\) e\([c,d]\), respectivamente.