14.8E: Exercícios para a Seção 14.8

Last updated
Save as PDF

Page ID: 188020

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1-15, use o método dos multiplicadores de Lagrange para encontrar os valores máximo e mínimo da função sujeita à restrição dada.

1) Função objetiva:$f(x, y) = 4xy$ Restrição:$\dfrac{x^2}{9} + \dfrac{y^2}{16} = 1$

Responda: Sujeito à restrição dada, a função$f$ tem um mínimo relativo de$-24$ em ambos$ \left(-\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $$ \left(\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $ e um máximo relativo de$24$ em ambos$ \left(\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $ e$ \left(-\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $

2) Função objetiva:$f(x, y) = x^2y$ Restrição:$x^2 + 2y^2 = 6$

3) Função objetiva:$f(x,y)=x^2 +y^2 +2x−2y+1$ Restrição:$ g(x,y)= x^2 +y^2 =2 $

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$-1$ at$ (-1, 1) $ e um máximo relativo de$7$ at$ (1,-1) $.

4) Função objetiva:$f(x, y) = xy$ Restrição:$4x^2 + 8y^2 = 16$

5) Função objetiva:$f(x, y) = x^2 + y^2$ Restrição:$xy = 1$

Responda: $f$tem um mínimo relativo de$2$ em ambos$ (-1, -1) $ e$ (1,1) $, sujeito à restrição dada.

6) Função objetiva:$f(x, y) = x^2 - y^2$ Restrição:$x−2y+6=0$

7) Função objetiva:$f(x, y) = x^2 + y^2$ Restrição:$x+2y−5=0$

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$ f(1,2)=5$ no ponto$ (1, 2) $.

8) Função objetiva:$f(x, y) = x^2 + y^2$ Restrição:$(x−1)^2+4y^2=4$

9) Função objetiva:$f(x, y) = 4x^3 + y^2$ Restrição:$2x^2 + y^2 = 1$

Responda: Sujeito à restrição dada, a função$f$ tem um mínimo relativo de$-\sqrt{2}$ at$ \left(-\frac{\sqrt{2}}{2}, 0\right) $,
um mínimo relativo de$\frac{25}{27}$ ambos os pontos$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $ e$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $,
um máximo relativo de$\sqrt{2}$ at$ \left(\frac{\sqrt{2}}{2}, 0\right) $ e um máximo relativo de $1$em ambos os pontos$ (0,1) $$ (0,-1) $ e.

Solução:: $g(x,y) = 2x^2 + y^2$Seja a função de restrição. Então:

$\vecs\nabla f(x,y) = 12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$ e$\vecs\nabla g(x,y) = 4x \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$

usando a equação do Multiplicador de Lagrange,\[\vecs\nabla f(x, y) = \lambda\vecs\nabla g(x, y),\nonumber \]
temos: nos\[12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j} = 4x\lambda \, \hat{\mathbf i} + 2y\lambda \,\hat{\mathbf j}\nonumber \]
dando o sistema de equações:\[12x^2 = 4x\lambda, \quad 2y = 2y\lambda, \quad \text{and the constraint}\quad 2x^2 + y^2 = 1\nonumber \]
Reescrevendo o primeiro duas equações como produtos zero (movendo-se para um lado e fatorando), obtemos:
\[\begin{align*} 4x(3x - \lambda) &= 0 & \text{and} && 2y(1 - \lambda) &= 0 \\ x = 0 \quad \text{or}\quad \lambda &= 3x & & &y = 0 \quad \text{or}\quad \lambda &= 1 \end{align*}\]
Agora, consideramos as combinações dessas soluções com as duas equações acima e conectamos cada uma delas à equação de restrição para resolver os pontos de Lagrange correspondentes.

A combinação$x = 0$ e$y = 0$ produz uma contradição quando colocada na equação de restrição, já que esse ponto não está na elipse.

Tomando a combinação$x = 0$ e$\lambda = 1$, colocamos para$0$$x$ na restrição e resolvemos para$y$, obtendo:$ y = \pm 1$. Isso nos dá dois pontos de Lagrange:$ (0, 1) $$ (0, -1)$ e.

Tomando a combinação$\lambda = 3x$ e$y = 0$, colocamos para$0$$y$ na restrição e resolvemos para$x$, obtendo:$ x = \pm \frac{\sqrt{2}}{2}$. Isso nos dá dois pontos de Lagrange:$ \left(-\frac{\sqrt{2}}{2}, 0\right) $$ \left(\frac{\sqrt{2}}{2}, 0\right) $ e.

Tomando a combinação$\lambda = 3x$ e$\lambda = 1$, substituímos$1$ na primeira equação por$\lambda$, dando-nos$ 1 = 3x$ isso$x = \frac{1}{3}$. Inserindo esse valor para$x$ na equação de restrição e resolvendo para$y$, obtemos o$y = \pm \frac{\sqrt{7}}{3}$ que nos dá os dois pontos de Lagrange:$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $ e.

Avaliando a função$f$ nesses pontos de Lagrange, encontramos:\[\begin{align*} f(0, -1) &= 1 & f(0, 1) &= 1 \\ f\left(-\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{-4(\sqrt{2})^3}{8} = -\sqrt{2} & f\left(\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{4(\sqrt{2})^3}{8} = \sqrt{2} \\ f\left(\tfrac{1}{3}, -\tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} & f\left(\tfrac{1}{3}, \tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} \end{align*}\]

Comparando esses valores com onde os pontos de Lagrange correspondentes estão na curva de restrição, concluímos os resultados declarados na resposta acima.

10) Função objetiva:$f(x,y)=2x^2 +y^2$ Restrição:$ g(x,y)= x^2 +y^2 =1 $

11) Função objetiva:$f(x,y,z)=x+3y−z$ Restrição:$ x^2+y^2+z^2=4 $

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$-2\sqrt{11}$ no ponto$ \left(-\frac{2\sqrt{11}}{11}, \, -\frac{6\sqrt{11}}{11}, \, \frac{2\sqrt{11}}{11}\right) $ e um máximo relativo de$2\sqrt{11}$ no ponto$ \left(\frac{2\sqrt{11}}{11}, \, \frac{6\sqrt{11}}{11}, \, -\frac{2\sqrt{11}}{11}\right).$

12) Função objetiva:$f(x, y, z) = x + y + z$ Restrição:$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$

13) Função objetiva:$f(x, y, z) = xyz$ Restrição:$x^2+2y^2+3z^2=6$

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$-\frac{2\sqrt{3}}{3}$$ \left( \sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),$ e$ \left( -\sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right) $ e um máximo relativo$\frac{2\sqrt{3}}{3}$ de$ \left( \sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),$$ \left( -\sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right) $ e.

14) Função objetiva:$f(x, y, z) = x^2 + y^2 + z^2$ Restrição:$x^4+y^4+z^4=1$

15) Função objetiva:$f(x, y, z) = x^2 + y^2 + z^2$ Restrição:$xyz=4$

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$ 6\sqrt[3]{2}$ pontos$ \left(\sqrt[3]{4},\,\sqrt[3]{4},\,\sqrt[3]{4}\right),$$ \left(\sqrt[3]{4},\,-\sqrt[3]{4},\,-\sqrt[3]{4}\right),$$ \left(-\sqrt[3]{4},\,\sqrt[3]{4},\,-\sqrt[3]{4}\right),$ e$ \left(-\sqrt[3]{4},\,-\sqrt[3]{4},\,\sqrt[3]{4}\right).$
Para ver uma visualização 3D desse problema, consulte: CalcPlot3d para o Problema 15.

Nos exercícios 16-21, use o método dos multiplicadores de Lagrange para encontrar a extremidade solicitada da função dada sujeita à restrição dada.

16) Maximize o$f(x,y) = \sqrt{6 - x^2 - y^2}$ sujeito à restrição,$ x+y−2=0$.

17) Maximize o$f(x,y) = x^2 - y^2$ sujeito às restrições,$ g(x,y)=y−x^2=0, \quad x>0,\quad y>0$.

Responda: Sujeito às restrições dadas,$f$ tem um máximo relativo de$ f\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)=\frac{1}{4}$ no ponto$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) $. Se não$x > 0$ fosse uma restrição, haveria dois outros pontos de Lagrange com extrema relativa$f$ sujeição às outras duas restrições. Isso teria sido$ (0, 0) $ e$ \left(-\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) .$

Para verificar se$f$ realmente tem um máximo relativo no ponto,$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right), $ precisaríamos verificar o valor de$f$ em ambos os lados desse ponto na curva de restrição,$y−x^2=0.$

Se$ x = 0.5$ qual é menor que$\frac{\sqrt{2}}{2}$,$y$ seria$ y = (0.5)^2 = 0.25.$
Se$ x = 1$ o que é maior que$\frac{\sqrt{2}}{2}$,$y$ seria$ y = (1)^2 = 1.$

Então comparamos o valor de $f$no ponto de Lagrange$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)$,, com os valores de$f$ nesses outros pontos da restrição.
Temos$f(0.5, 0.25) = (0.5)^2 - (0.25)^2 = 0.25 - 0.0625 = 0.1875 < \frac{1}{4}$ e,$f(1, 1) = (1)^2 - (1)^2 = 0 < \frac{1}{4}.$

portanto, podemos concluir que, de$f$ fato, tem um máximo relativo de$\frac{1}{4}$ no ponto$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right).$

18) Maximize o$U(x,y) = 8x^{4/5}y^{1/5}$ sujeito à restrição,$ 4x+2y=12$.

19) Minimize$f(x,y,z)=x^2+y^2+z^2$ sujeito à restrição,$x+y+z=1$.

Responda: Sujeito à restrição dada,$f$ tem um mínimo relativo de$ f\left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right)=\frac{1}{3}$ no ponto$ \left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right) $.

20) Minimize$f(x,y)=xy$ na elipse$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$.

21) Maximize$f(x,y,z)=2x+3y+5z$ na esfera$x^2+y^2+z^2=19$.

Responda: Sujeito à restrição dada,$f$ tem um máximo relativo de$ 19\sqrt{2} $ no ponto$ \left( \sqrt{2},\, \frac{3\sqrt{2}}{2},\, \frac{5\sqrt{2}}{2} \right) $.
Observe que, sujeito a essa restrição,$f$ também tem um mínimo relativo de$ -19\sqrt{2} $ no ponto$ \left( -\sqrt{2},\, -\frac{3\sqrt{2}}{2},\, -\frac{5\sqrt{2}}{2} \right) $.
Para ver uma visualização em 3D desse problema, consulte: CalcPlot3D para o Problema 21.

Nos exercícios 22-23, use o método dos multiplicadores de Lagrange com duas restrições.

22) Otimize$f(x,y,z)=yz+xy$ de acordo com as restrições:$xy=1, \quad y^2+z^2=1$.

Responda: máximo:$\frac{3}{2}$, mínimo:$\frac{1}{2}$

23) Minimize$f(x,y,z)=x^2+y^2+z^2$ quando$x+y+z=9$$x+2y+3z=20$ e.

Responda: mínimo:$f(2,3,4)=29$

Use o método dos multiplicadores de Lagrange para resolver os seguintes problemas aplicados.

24) Um recipiente grande na forma de um sólido retangular deve ter um volume de 480 m ³. A parte inferior do contêiner custa $5/m ² para ser construída, enquanto a parte superior e as laterais custam $3/m ² para construir. Use multiplicadores de Lagrange para encontrar as dimensões do contêiner desse tamanho que tenha o custo mínimo.

25) Uma caixa retangular sem tampa (uma caixa de topless) deve ser feita de 12 pés ² de papelão. Encontre o volume máximo dessa caixa.

Responda: O volume máximo é$4$ ft ³. As dimensões são$1×2×2$ pés.

26) Encontre a distância mínima da parábola$y=x^2$ até o ponto$(0,3)$.

27) Encontre o ponto na linha$y=2x+3$ que está mais próximo do ponto$(4,2)$.

Responda: $ (25,195) $

29) Encontre a distância mínima do ponto$(0,1)$ até a parábola$x^2=4y.$

Responda: $1.0$unidade

30) Encontre as distâncias mínima e máxima entre a elipse$x^2+xy+2y^2=1$ e a origem.

31) Encontre a distância mínima do avião$x+y+z=1$ até o ponto$(2,1,1)$.

Responda: $\sqrt{3}$unidades

32) Encontre o ponto no plano$4x+3y+z=2 $ que está mais próximo do ponto$(1,−1,1)$.

33) Encontre o ponto na superfície$x^2−2xy+y^2−x+y=0$ mais próximo do ponto$(1,2,−3).$

Responda: $ \left(1,\,\frac{1}{2},\,−3\right) $

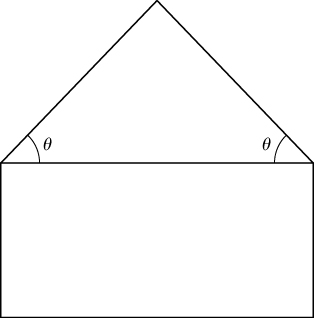
34) Um pentágono é formado colocando um triângulo isósceles em um retângulo, conforme mostrado no diagrama. Se o perímetro do pentágono for de 10 polegadas, encontre os comprimentos dos lados do pentágono que maximizarão a área do pentágono.

$CNX_Calc_Figure_14_08_201.jpg$

35) [T] Ao investir$x$ unidades de trabalho e$y$ unidades de capital, um fabricante de relógios pode produzir$P(x,y)=50x^{0.4}y^{0.6}$ relógios. Encontre o número máximo de relógios que podem ser produzidos com um orçamento de $20.000 se a mão de obra custar $100/unidade e o capital custar $200/unidade. Use um gráfico como CalcPlot3D para esboçar um gráfico de contorno da função.

Responda

Aproximadamente 3365 relógios no ponto crítico ($80,60).$

$Uma série de curvas no primeiro quadrante, com a primeira começando perto (2.120), diminuindo bruscamente para perto (20, 20) e depois diminuindo lentamente para (120, 5). A próxima curva começa perto de (10, 120), diminui bruscamente para perto (40, 40) e depois diminui lentamente para (120, 20). A próxima curva começa perto de (20, 120), diminui bruscamente para perto (60, 60) e depois diminui lentamente para (120, 40). A próxima curva começa perto de (40, 120), diminui para perto (80, 80) e depois diminui um pouco lentamente para (120, 60). A última curva começa perto de (60, 120) e diminui de forma bastante uniforme de (100, 100) até (120, 90).$

36) Um sólido retangular está contido em um tetraedro com vértices em$(1,0,0),\,(0,1,0),\,(0,0,1)$ e a origem. A base da caixa tem dimensões$x$ e$y$, e a altura da caixa é$z$. Se a soma de$x$$y$, e$z$ for$1$, encontre as dimensões que maximizam o volume do sólido retangular.

37) Encontre o valor máximo de$f(x,y)=\sin x\sin y,$ onde$x$ e$y$ denote os ângulos agudos de um triângulo reto. Desenhe o gráfico de superfície e o gráfico de contorno da função usando um CAS.

Responda: Sujeito a essa restrição,$f$ tem um máximo relativo de$\frac{1}{2}$ quando$x = \frac{\pi}{4}$$y = \frac{\pi}{4}$ e.
Gráfico de superfície e gráfico de contorno para$f$: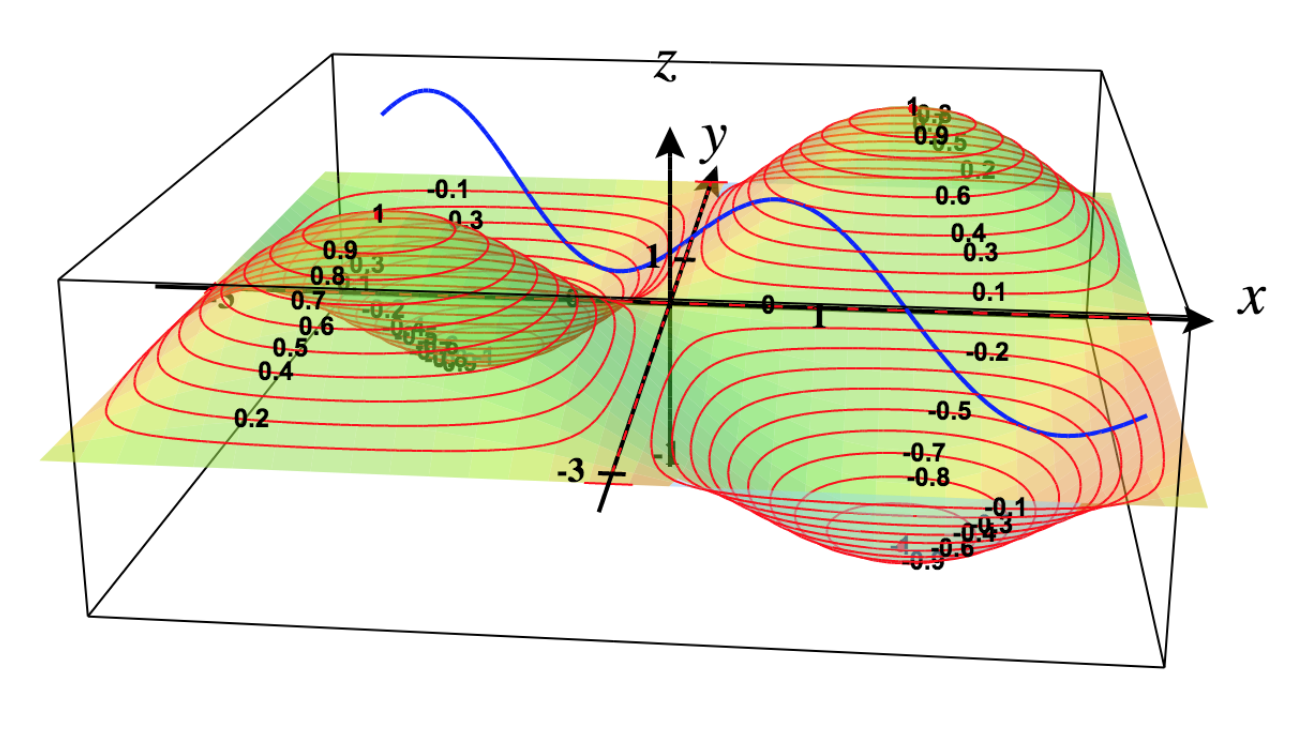
$Uma série alternada de colinas e vales de amplitude 1 no espaço xyz.$ $Gráfico de contorno para f (x, y) = sin x sin y$

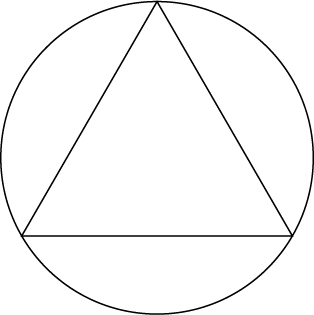
38) Mostre que, de todos os triângulos inscritos em um círculo de raio$R$ (veja o diagrama), o triângulo equilátero tem o maior perímetro.

$Um círculo com um triângulo equilátero desenhado dentro dele de forma que cada vértice do triângulo toque o círculo.$

Contributors

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) reordered these problems, adding problems 3 and 10 and answers for problems 15 and 17. He also added a full worked-out solution for problem 9 and a link to CalcPlot3D in problems 15, 21 and 35. He also created new images for Problem 37 and expanded the answers for many problems.