14.8: Multiplicadores de Lagrange

Objetivos de

• Use o método dos multiplicadores de Lagrange para resolver problemas de otimização com uma restrição.
• Use o método dos multiplicadores de Lagrange para resolver problemas de otimização com duas restrições.

Resolver problemas de otimização para funções de duas ou mais variáveis pode ser semelhante a resolver esses problemas no cálculo de variável única. No entanto, técnicas para lidar com várias variáveis nos permitem resolver problemas de otimização mais variados para os quais precisamos lidar com condições ou restrições adicionais. Nesta seção, examinamos um dos métodos mais comuns e úteis para resolver problemas de otimização com restrições.

Multiplicadores de Lagrange

Na seção anterior, uma situação aplicada foi explorada envolvendo a maximização de uma função de lucro, sujeita a certas restrições. Nesse exemplo, as restrições envolviam um número máximo de bolas de golfe que poderiam ser produzidas e vendidas em um\(1\) mês\((x),\) e um número máximo de horas de publicidade que poderiam ser compradas por mês\((y)\). Suponha que eles tenham sido combinados em uma única restrição orçamentária, como\(20x+4y≤216\), por exemplo, que levou em consideração o custo de produção das bolas de golfe e o número de horas de publicidade compradas por mês. O objetivo ainda é maximizar o lucro, mas agora há um tipo diferente de restrição nos valores de\(x\)\(y\) e. Essa restrição e a função de lucro correspondente

\[f(x,y)=48x+96y−x^2−2xy−9y^2 \nonumber \]

é um exemplo de um problema de otimização, e a função\(f(x,y)\) é chamada de função objetivo. Segue um gráfico de várias curvas de nível\(f(x,y)\) da função.

Figura\(\PageIndex{1}\): Gráfico mostrando as curvas de nível da função\(f(x,y)=48x+96y−x^2−2xy−9y^2\) correspondente a\(c=150,250,350,\) e\(400.\)

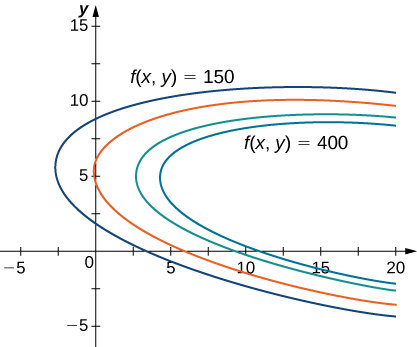
Na Figura\(\PageIndex{1}\), o valor\(c\) representa diferentes níveis de lucro (ou seja, valores da função\(f\)). Conforme o valor de\(c\) aumenta, a curva muda para a direita. Como nosso objetivo é maximizar o lucro, queremos escolher uma curva o mais à direita possível. Se não houvesse restrições quanto ao número de bolas de golfe que a empresa poderia produzir ou ao número de unidades de publicidade disponíveis, poderíamos produzir quantas bolas de golfe quisermos e anunciar o quanto quisermos, e não haveria um lucro máximo para a empresa. Infelizmente, temos uma restrição orçamentária que é modelada pela desigualdade.\(20x+4y≤216.\) Para ver como essa restrição interage com a função de lucro, a Figura\(\PageIndex{2}\) mostra o gráfico da linha\(20x+4y=216\) sobreposta no gráfico anterior.

Figura\(\PageIndex{2}\): Gráfico das curvas de nível da função\(f(x,y)=48x+96y−x^2−2xy−9y^2\) correspondente a\(c=150,250,350,\)\(395\) e. O gráfico vermelho é a função de restrição.

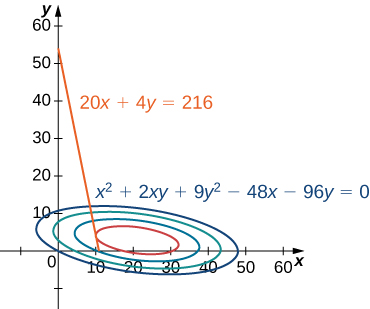
Conforme mencionado anteriormente, o lucro máximo ocorre quando a curva de nível está o mais à direita possível. No entanto, o nível de produção correspondente a esse lucro máximo também deve satisfazer a restrição orçamentária, portanto, o ponto em que esse lucro ocorre também deve estar (ou à esquerda) da linha vermelha na Figura\(\PageIndex{2}\). A inspeção deste gráfico revela que esse ponto existe onde a linha é tangente à curva de nível de\(f\). Tentativa e erro revelam que esse nível de lucro parece estar próximo\(395\), quando\(x\) e ambos\(y\) são um pouco menores que\(5\). Retornaremos à solução desse problema posteriormente nesta seção. Do ponto de vista teórico, no ponto em que a curva de lucro é tangente à linha de restrição, o gradiente de ambas as funções avaliadas nesse ponto deve apontar na mesma direção (ou oposta). Lembre-se de que o gradiente de uma função de mais de uma variável é um vetor. Se dois vetores apontarem nas mesmas direções (ou opostas), então um deve ser um múltiplo constante do outro. Essa ideia é a base do método dos multiplicadores de Lagrange.

Método de multiplicadores de Lagrange: uma restrição

Teorema\(\PageIndex{1}\):\(g\) Seja\(f\) e seja funções de duas variáveis com derivadas parciais contínuas em cada ponto de algum conjunto aberto contendo a curva suave\(g(x,y)=0.\) Suponha que\(f\), quando restrito a pontos na curva\(g(x,y)=0\), tenha uma extremidade local no ponto\((x_0,y_0)\) e isso\(\vecs ∇g(x_0,y_0)≠0\). Depois, há um número\(λ\) chamado multiplicador de Lagrange, para o qual

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0). \nonumber \]

Prova

Suponha que uma extremidade restrita ocorra no ponto.\((x_0,y_0).\) Além disso, assumimos que a equação\(g(x,y)=0\) pode ser facilmente parametrizada como

\(x=x(s) \; \text{and}\; y=y(s)\)

onde\(s\) é um parâmetro de comprimento de arco com ponto de referência\((x_0,y_0)\) em\(s=0\). Portanto, a quantidade\(z=f(x(s),y(s))\) tem um máximo relativo ou mínimo relativo em\(s=0\), e isso implica que nesse\(\dfrac{dz}{ds}=0\) ponto. Da regra da cadeia,

\[\begin{align*} \dfrac{dz}{ds} &=\dfrac{∂f}{∂x}⋅\dfrac{∂x}{∂s}+\dfrac{∂f}{∂y}⋅\dfrac{∂y}{∂s} \\[4pt] &=\left(\dfrac{∂f}{∂x}\hat{\mathbf i}+\dfrac{∂f}{∂y}\hat{\mathbf j}\right)⋅\left(\dfrac{∂x}{∂s}\hat{\mathbf i}+\dfrac{∂y}{∂s}\hat{\mathbf j}\right)\\[4pt] &=0, \end{align*}\]

onde as derivadas são todas avaliadas\(s=0\). No entanto, o primeiro fator no produto escalar é o gradiente de\(f\), e o segundo fator é o vetor tangente unitário\(\vec{\mathbf T}(0)\) à curva de restrição. Como o ponto\((x_0,y_0)\) corresponde a\(s=0\), decorre dessa equação que

\[\vecs ∇f(x_0,y_0)⋅\vecs{\mathbf T}(0)=0, \nonumber \]

o que implica que o gradiente é o vetor zero\(\vecs 0\) ou é normal para a curva de restrição em uma extremidade relativa restrita. No entanto, a curva de restrição\(g(x,y)=0\) é uma curva de nível para a função\(g(x,y)\), de modo que\(\vecs ∇g(x_0,y_0)≠0\), se então\(\vecs ∇g(x_0,y_0)\) for normal para essa curva em\((x_0,y_0)\) Segue-se, então, que existe algum escalar\(λ\) tal que

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0) \nonumber \]

\(\square\)

Para aplicar o Teorema\(\PageIndex{1}\) a um problema de otimização semelhante ao do fabricante da bola de golfe, precisamos de uma estratégia de resolução de problemas.

Estratégia de resolução de problemas: etapas para usar multiplicadores de Lagrange

1. Determine a função objetivo\(f(x,y)\) e a função de restrição\(g(x,y).\) O problema de otimização envolve maximizar ou minimizar a função objetivo?
2. Configure um sistema de equações usando o seguinte modelo:\[\begin{align} \vecs ∇f(x_0,y_0) &=λ\vecs ∇g(x_0,y_0) \\[4pt] g(x_0,y_0) &=0 \end{align}. \nonumber \]
3. Resolva para\(x_0\)\(y_0\) e.
4. O maior dos valores de\(f\) at nas soluções encontradas na etapa\(3\) maximiza\(f\); o menor desses valores é minimizado\(f\).

Exemplo\(\PageIndex{1}\): Using Lagrange Multipliers

Use o método dos multiplicadores de Lagrange para encontrar o valor mínimo de\(f(x,y)=x^2+4y^2−2x+8y\) sujeito à restrição\(x+2y=7.\)

Solução

Vamos seguir a estratégia de resolução de problemas:

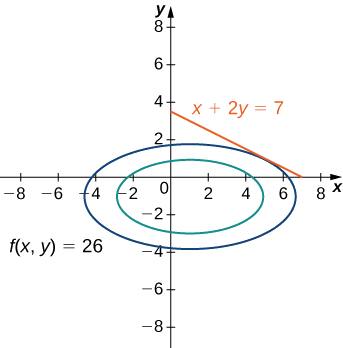
1. A função objetivo é\(f(x,y)=x^2+4y^2−2x+8y.\) Para determinar a função de restrição, devemos primeiro subtrair\(7\) de ambos os lados da restrição. Isso dá\(x+2y−7=0.\) A função de restrição é igual ao lado esquerdo, então\(g(x,y)=x+2y−7\). O problema pede que resolvamos o valor mínimo de\(f\), sujeito à restrição (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Gráfico das curvas de nível da função\(f(x,y)=x^2+4y^2−2x+8y\) correspondente a\(c=10\)\(26\) e. O gráfico vermelho é a função de restrição.

2. Em seguida, devemos calcular os gradientes de ambos\(f\) e\(g\):

\[\begin{align*} \vecs \nabla f \left( x, y \right) &= \left( 2x - 2 \right) \hat{\mathbf{i}} + \left( 8y + 8 \right) \hat{\mathbf{j}} \\ \vecs \nabla g \left( x, y \right) &= \hat{\mathbf{i}} + 2 \hat{\mathbf{j}}. \end{align*}\]

A equação\(\vecs \nabla f \left( x_0, y_0 \right) = \lambda \vecs \nabla g \left( x_0, y_0 \right)\) se torna

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \left( \hat{\mathbf{i}} + 2 \hat{\mathbf{j}} \right), \nonumber \]

que pode ser reescrito como

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \hat{\mathbf{i}} + 2 \lambda \hat{\mathbf{j}}. \nonumber \]

Em seguida, definimos os coeficientes\(\hat{\mathbf{i}}\) e\(\hat{\mathbf{j}}\) iguais entre si:

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda. \end{align*}\]

A equação\(g \left( x_0, y_0 \right) = 0\) se torna\(x_0 + 2 y_0 - 7 = 0\). Portanto, o sistema de equações que precisa ser resolvido é

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda \\ x_0 + 2 y_0 - 7 &= 0. \end{align*}\]

3. Este é um sistema linear de três equações em três variáveis. Começamos resolvendo a segunda equação\(λ\) e substituindo-a pela primeira equação. Isso dá\(λ=4y_0+4\), então, substituir isso na primeira equação dá\[2x_0−2=4y_0+4.\nonumber \] Resolver esta equação por\(x_0\) dá\(x_0=2y_0+3\). Em seguida, substituímos isso na terceira equação:

\[\begin{align*} (2y_0+3)+2y_0−7 =0 \\[4pt]4y_0−4 =0 \\[4pt]y_0 =1. \end{align*}\]

Uma vez que\(x_0=2y_0+3,\) isso dá\(x_0=5.\)

4. Em seguida, avaliamos\(f(x,y)=x^2+4y^2−2x+8y\) no ponto\((5,1)\):\[f(5,1)=5^2+4(1)^2−2(5)+8(1)=27. \nonumber \] Para garantir que isso corresponda a um valor mínimo na função de restrição, vamos tentar alguns outros pontos na restrição de ambos os lados do ponto\((5,1)\), como as interceptações de\(g(x,y)=0\), Quais são\((7,0)\)\((0,3.5)\) e.

Nós recebemos\(f(7,0)=35 \gt 27\)\(f(0,3.5)=77 \gt 27\) e.

Portanto, parece que\(f\) tem um mínimo relativo de\(27\) at\((5,1)\), sujeito à restrição dada.

Exercício\(\PageIndex{1}\)

Use o método dos multiplicadores de Lagrange para encontrar o valor máximo de

\[f(x,y)=9x^2+36xy−4y^2−18x−8y \nonumber \]

sujeito à restrição\(3x+4y=32.\)

Dica

Use a estratégia de resolução de problemas para o método dos multiplicadores de Lagrange.

Resposta

Sujeito à restrição dada,\(f\) tem um valor máximo de\(976\) no ponto\((8,2)\).

Vamos agora voltar ao problema apresentado no início da seção.

Exemplo\(\PageIndex{2}\): Golf Balls and Lagrange Multipliers

O fabricante de bolas de golfe, Pro-T, desenvolveu um modelo de lucro que depende do número\(x\) de bolas de golfe vendidas por mês (medido em milhares) e do número de horas por mês de publicidade y, de acordo com a função

\[z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]

onde\(z\) é medido em milhares de dólares. A função de restrição orçamentária que relaciona o custo de produção de milhares de bolas de golfe e unidades publicitárias é dada por\(20x+4y=216.\) Encontre os valores de\(x\) e\(y\) que maximizam o lucro e encontre o lucro máximo.

Solução:

Novamente, seguimos a estratégia de resolução de problemas:

1. A função objetivo é\(f(x,y)=48x+96y−x^2−2xy−9y^2.\) Para determinar a função de restrição, primeiro subtraímos\(216\) de ambos os lados da restrição e, em seguida, dividimos os dois lados por\(4\),\(5x+y−54=0.\) o que dá A função de restrição é igual ao lado esquerdo, então\(g(x,y)=5x+y−54.\) O problema nos pede para resolver o valor máximo de\(f\), sujeito a essa restrição.
2. Então, calculamos os gradientes de ambos\(f\) e\(g\):\[\begin{align*} \vecs ∇f(x,y) &=(48−2x−2y)\hat{\mathbf i}+(96−2x−18y)\hat{\mathbf j}\\[4pt]\vecs ∇g(x,y) &=5\hat{\mathbf i}+\hat{\mathbf j}. \end{align*}\] A equação\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\) se torna\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ(5\hat{\mathbf i}+\hat{\mathbf j}),\nonumber \] que pode ser reescrita à medida que\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ5\hat{\mathbf i}+λ\hat{\mathbf j}.\nonumber \] definimos os coeficientes\(\hat{\mathbf i}\) e\(\hat{\mathbf j}\) iguais entre si:\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ. \end{align*}\] A equação\(g(x_0,y_0)=0\) se torna\(5x_0+y_0−54=0\). Portanto, o sistema de equações que precisa ser resolvido é\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ \\[4pt]5x_0+y_0−54 =0. \end{align*}\]
3. Usamos o lado esquerdo da segunda equação para substituir\(λ\) na primeira equação:\[\begin{align*} 48−2x_0−2y_0 &=5(96−2x_0−18y_0) \\[4pt]48−2x_0−2y_0 &=480−10x_0−90y_0 \\[4pt] 8x_0 &=432−88y_0 \\[4pt] x_0 &=54−11y_0. \end{align*}\] Em seguida, substituímos isso pela terceira equação:\[\begin{align*} 5(54−11y_0)+y_0−54 &=0\\[4pt] 270−55y_0+y_0-54 &=0\\[4pt]216−54y_0 &=0 \\[4pt]y_0 &=4. \end{align*}\] Uma vez que\(x_0=54−11y_0,\) isso dá\(x_0=10.\)
4. Em seguida,\((10,4)\) substituímos o\(f(x,y)=48x+96y−x^2−2xy−9y^2,\) que dá\[\begin{align*} f(10,4) &=48(10)+96(4)−(10)^2−2(10)(4)−9(4)^2 \\[4pt] &=480+384−100−80−144 \\[4pt] &=540.\end{align*}\] Portanto, o lucro máximo que pode ser alcançado, sujeito a restrições orçamentárias, é\($540,000\) com um nível de produção de bolas de\(10,000\) golfe e\(4\) horas de publicidade compradas por mês. Vamos verificar se isso realmente é o máximo. Os pontos finais da linha que define a restrição são\((10.8,0)\) e\((0,54)\) Vamos avaliar\(f\) em ambos os pontos:\[\begin{align*} f(10.8,0) &=48(10.8)+96(0)−10.8^2−2(10.8)(0)−9(0^2) \\[4pt] &=401.76 \\[4pt] f(0,54) &=48(0)+96(54)−0^2−2(0)(54)−9(54^2) \\[4pt] &=−21,060. \end{align*}\] O segundo valor representa uma perda, já que nenhuma bola de golfe é produzida. Nenhum desses valores excede\(540\), então parece que nosso extremo é um valor máximo de\(f\), sujeito à restrição dada.

Exercício\(\PageIndex{2}\): Optimizing the Cobb-Douglas function

Uma empresa determinou que seu nível de produção é dado pela função Cobb-Douglas,\(f(x,y)=2.5x^{0.45}y^{0.55}\) onde\(x\) representa o número total de horas de trabalho no\(1\) ano e\(y\) representa a entrada total de capital para a empresa. Suponha custos\(1\) unitários de mão de obra\($40\) e\(1\) unidade de custos de capital\($50\). Use o método dos multiplicadores de Lagrange para encontrar o valor máximo de\(f(x,y)=2.5x^{0.45}y^{0.55}\) sujeito a uma restrição orçamentária de\($500,000\) por ano.

Dica

Use a estratégia de resolução de problemas para o método dos multiplicadores de Lagrange.

Resposta

Sujeito à restrição dada, um nível máximo de produção de\(13890\) ocorre com as horas de\(5625\) trabalho e com a entrada total\($5500\) de capital.

No caso de uma função objetiva com três variáveis e uma única função de restrição, é possível usar o método dos multiplicadores de Lagrange para resolver também um problema de otimização. Um exemplo de uma função objetiva com três variáveis poderia ser a função Cobb-Douglas no Exercício\(\PageIndex{2}\):\(f(x,y,z)=x^{0.2}y^{0.4}z^{0.4},\) onde\(x\) representa o custo do trabalho,\(y\) representa a entrada de capital e\(z\) representa o custo da publicidade. O método é o mesmo do método com uma função de duas variáveis; as equações a serem resolvidas são

\[\begin{align*} \vecs ∇f(x,y,z) &=λ\vecs ∇g(x,y,z) \\[4pt] g(x,y,z) &=0. \end{align*}\]

Exemplo\(\PageIndex{3}\): Lagrange Multipliers with a Three-Variable objective function

Maximize a função\(f(x,y,z)=x^2+y^2+z^2\) sujeita à restrição\(x+y+z=1.\)

Solução

1. A função objetivo é\(f(x,y,z)=x^2+y^2+z^2.\) Para determinar a função de restrição, subtraímos\(1\) de cada lado da restrição: o\(x+y+z−1=0\) que fornece a função de restrição como\(g(x,y,z)=x+y+z−1.\)

2. Em seguida, calculamos\(\vecs ∇f(x,y,z)\) e\(\vecs ∇g(x,y,z):\)\[\begin{align*} \vecs ∇f(x,y,z) &=⟨2x,2y,2z⟩ \\[4pt] \vecs ∇g(x,y,z) &=⟨1,1,1⟩. \end{align*}\] isso leva às equações\[\begin{align*} ⟨2x_0,2y_0,2z_0⟩ &=λ⟨1,1,1⟩ \\[4pt] x_0+y_0+z_0−1 &=0 \end{align*}\] que podem ser reescritas da seguinte forma:\[\begin{align*} 2x_0 &=λ\\[4pt] 2y_0 &=λ \\[4pt] 2z_0 &=λ \\[4pt] x_0+y_0+z_0−1 &=0. \end{align*}\]

3. Como cada uma das três primeiras equações está\(λ\) no lado direito, sabemos disso\(2x_0=2y_0=2z_0\) e todas as três variáveis são iguais entre si. Substituir\(y_0=x_0\) e\(z_0=x_0\) na última equação produz\(3x_0−1=0,\) assim\(x_0=\frac{1}{3}\) e\(y_0=\frac{1}{3}\) e\(z_0=\frac{1}{3}\) que corresponde a um ponto crítico na curva de restrição.

4. Em seguida, avaliamos\(f\) no ponto\(\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\):\[f\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2=\dfrac{3}{9}=\dfrac{1}{3} \nonumber \] Portanto, um possível extremo da função é\(\frac{1}{3}\). Para verificar se é mínimo, escolha outros pontos que satisfaçam a restrição de ambos os lados do ponto que obtivemos acima e calcule\(f\) nesses pontos. Por exemplo,\[\begin{align*} f(1,0,0) &=1^2+0^2+0^2=1 \\[4pt] f(0,−2,3) &=0^2++(−2)^2+3^2=13. \end{align*}\] ambos os valores são maiores que\(\frac{1}{3}\), o que nos leva a acreditar que o extremo é um mínimo, sujeito à restrição dada.

Exercício\(\PageIndex{3}\)

Use o método dos multiplicadores de Lagrange para encontrar o valor mínimo da função

\[f(x,y,z)=x+y+z \nonumber \]

sujeito à restrição\(x^2+y^2+z^2=1.\)

Dica

Use a estratégia de resolução de problemas para o método dos multiplicadores de Lagrange com uma função objetiva de três variáveis.

Resposta

Avaliando\(f\) em ambos os pontos que obtivemos, nos dá:\[\begin{align*} f\left(\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3}\right) =\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}=\sqrt{3} \\ f\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right) =−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}=−\sqrt{3}\end{align*}\] Como a restrição é contínua, comparamos esses valores e concluímos que\(f\) tem um mínimo relativo de\(−\sqrt{3}\) no ponto\(\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right)\), sujeito à restrição dada.

Problemas com duas restrições

O método dos multiplicadores de Lagrange pode ser aplicado a problemas com mais de uma restrição. Nesse caso, a função objetivo\(w\) é uma função de três variáveis:

\[w=f(x,y,z) \nonumber \]

e está sujeito a duas restrições:

\[g(x,y,z)=0 \; \text{and} \; h(x,y,z)=0. \nonumber \]

Existem dois multiplicadores de Lagrange\(λ_1\) e\(λ_2\), e o sistema de equações se torna

\[\begin{align*} \vecs ∇f(x_0,y_0,z_0) &=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0) \\[4pt] g(x_0,y_0,z_0) &=0\\[4pt] h(x_0,y_0,z_0) &=0 \end{align*}\]

Exemplo\(\PageIndex{4}\): Lagrange Multipliers with Two Constraints

Encontre os valores máximo e mínimo da função

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

sujeito às restrições\(z^2=x^2+y^2\) e\(x+y−z+1=0.\)

Solução

Vamos seguir a estratégia de resolução de problemas:

1. A função objetivo é\(f(x,y,z)=x^2+y^2+z^2.\) Para determinar as funções de restrição, primeiro subtraímos\(z^2\) de ambos os lados da primeira restrição, o que dá\(x^2+y^2−z^2=0\), então\(g(x,y,z)=x^2+y^2−z^2\). A segunda função de restrição é\(h(x,y,z)=x+y−z+1.\)
2. Em seguida, calculamos os gradientes de\(f,g,\) e\(h\):\[\begin{align*} \vecs ∇f(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}+2z\hat{\mathbf k} \\[4pt] \vecs ∇g(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}−2z\hat{\mathbf k} \\[4pt] \vecs ∇h(x,y,z) &=\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}. \end{align*}\] A equação\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\) se torna a\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=λ_1(2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}−2z_0\hat{\mathbf k})+λ_2(\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}), \nonumber \] que pode ser reescrita como\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=(2λ_1x_0+λ_2)\hat{\mathbf i}+(2λ_1y_0+λ_2)\hat{\mathbf j}−(2λ_1z_0+λ_2)\hat{\mathbf k}. \nonumber \] Próxima, definimos os coeficientes\(\hat{\mathbf i}\) e\(\hat{\mathbf j}\) iguais entre si:\[\begin{align*}2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2. \end{align*}\] As duas equações que surgem das restrições são \(z_0^2=x_0^2+y_0^2\)\(x_0+y_0−z_0+1=0\)e. A combinação dessas equações com as três equações anteriores dá\[\begin{align*} 2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2 \\[4pt]z_0^2 &=x_0^2+y_0^2 \\[4pt]x_0+y_0−z_0+1 &=0. \end{align*}\]
3. As três primeiras equações contêm a variável\(λ_2\). Resolver a terceira equação\(λ_2\) e substituí-la pela primeira e segunda equações reduz o número de equações para quatro:\[\begin{align*}2x_0 &=2λ_1x_0−2λ_1z_0−2z_0 \\[4pt] 2y_0 &=2λ_1y_0−2λ_1z_0−2z_0\\[4pt] z_0^2 &=x_0^2+y_0^2\\[4pt] x_0+y_0−z_0+1 &=0. \end{align*}\] Em seguida, resolvemos a primeira e a segunda equação para\(λ_1\). A primeira equação dá\(λ_1=\dfrac{x_0+z_0}{x_0−z_0}\), a segunda equação dá\(λ_1=\dfrac{y_0+z_0}{y_0−z_0}\). Definimos o lado direito de cada equação igual um ao outro e multiplicamos cruzadamente:\[\begin{align*} \dfrac{x_0+z_0}{x_0−z_0} &=\dfrac{y_0+z_0}{y_0−z_0} \\[4pt](x_0+z_0)(y_0−z_0) &=(x_0−z_0)(y_0+z_0) \\[4pt]x_0y_0−x_0z_0+y_0z_0−z_0^2 &=x_0y_0+x_0z_0−y_0z_0−z_0^2 \\[4pt]2y_0z_0−2x_0z_0 &=0 \\[4pt]2z_0(y_0−x_0) &=0. \end{align*}\] Portanto, ou\(z_0=0\) ou\(y_0=x_0\). Se\(z_0=0\), então a primeira restrição se torna\(0=x_0^2+y_0^2\). A única solução real para essa equação é\(x_0=0\) e\(y_0=0\), que dá o triplo ordenado\((0,0,0)\). Esse ponto não satisfaz a segunda restrição, então não é uma solução. Em seguida, consideramos\(y_0=x_0\), o que reduz o número de equações para três:\[\begin{align*}y_0 &= x_0 \\[4pt] z_0^2 &= x_0^2 +y_0^2 \\[4pt] x_0 + y_0 -z_0+1 &=0. \end{align*} \nonumber \] Substituímos a primeira equação na segunda e terceira equações:\[\begin{align*} z_0^2 &= x_0^2 +x_0^2 \\[4pt] &= x_0+x_0-z_0+1 &=0. \end{align*} \nonumber \] Então, resolvemos a segunda equação para\(z_0\), que dá\(z_0=2x_0+1\). Em seguida, substituímos isso na primeira equação\[\begin{align*} z_0^2 &= 2x_0^2 \\[4pt] (2x_0^2 +1)^2 &= 2x_0^2 \\[4pt] 4x_0^2 + 4x_0 +1 &= 2x_0^2 \\[4pt] 2x_0^2 +4x_0 +1 &=0, \end{align*}\] e usamos a fórmula quadrática para resolver\(x_0\):\[ x_0 = \dfrac{-4 \pm \sqrt{4^2 -4(2)(1)} }{2(2)} = \dfrac{-4\pm \sqrt{8}}{4} = \dfrac{-4 \pm 2\sqrt{2}}{4} = -1 \pm \dfrac{\sqrt{2}}{2}. \nonumber \] Recall\(y_0=x_0\), então isso\(y_0\) também resolve. Então\(z_0=2x_0+1\),\[z_0 = 2x_0 +1 =2 \left( -1 \pm \dfrac{\sqrt{2}}{2} \right) +1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2} . \nonumber \] portanto, existem duas soluções trigêmeas ordenadas:\[\left( -1 + \dfrac{\sqrt{2}}{2} , -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) \; \text{and} \; \left( -1 -\dfrac{\sqrt{2}}{2} , -1 -\dfrac{\sqrt{2}}{2} , -1 -\sqrt{2} \right). \nonumber \]
4. Substituímos\(\left(−1+\dfrac{\sqrt{2}}{2},−1+\dfrac{\sqrt{2}}{2}, −1+\sqrt{2}\right) \) em\(f(x,y,z)=x^2+y^2+z^2\), o que dá\[\begin{align*} f\left( -1 + \dfrac{\sqrt{2}}{2}, -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) &= \left( -1+\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 + \dfrac{\sqrt{2}}{2} \right)^2 + (-1+\sqrt{2})^2 \\[4pt] &= \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + (1 -2\sqrt{2} +2) \\[4pt] &= 6-4\sqrt{2}. \end{align*}\] Então, substituímos\(\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2}\right)\) em\(f(x,y,z)=x^2+y^2+z^2\), que dá\[\begin{align*} f\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2} \right) &= \left( -1-\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 - \dfrac{\sqrt{2}}{2} \right)^2 + (-1-\sqrt{2})^2 \\[4pt] &= \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + (1 +2\sqrt{2} +2) \\[4pt] &= 6+4\sqrt{2}. \end{align*}\]\(6+4\sqrt{2}\) é o valor máximo e\(6−4\sqrt{2}\) é o valor mínimo de\(f(x,y,z)\), sujeito às restrições dadas.

Exercício\(\PageIndex{4}\)

Use o método dos multiplicadores de Lagrange para encontrar o valor mínimo da função

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

sujeito às restrições\(2x+y+2z=9\) e\(5x+5y+7z=29.\)

Dica

Use a estratégia de resolução de problemas para o método dos multiplicadores de Lagrange com duas restrições.

Resposta

\(f(2,1,2)=9\)é um valor mínimo de\(f\), sujeito às restrições dadas.

Conceitos-chave

• Uma função objetiva combinada com uma ou mais restrições é um exemplo de um problema de otimização.
• Para resolver problemas de otimização, aplicamos o método dos multiplicadores de Lagrange usando uma estratégia de resolução de problemas em quatro etapas.

Equações-chave

• Método de multiplicadores de Lagrange, uma restrição

\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\)

\(g(x_0,y_0)=0\)

• Método de multiplicadores de Lagrange, duas restrições

\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\)

\(g(x_0,y_0,z_0)=0\)

\(h(x_0,y_0,z_0)=0\)

Glossário

restrição

uma desigualdade ou equação envolvendo uma ou mais variáveis que é usada em um problema de otimização; a restrição impõe um limite nas possíveis soluções para o problema

Multiplicador de Lagrange

a constante (ou constantes) usada no método dos multiplicadores de Lagrange; no caso de uma constante, ela é representada pela variável\(λ\)

método dos multiplicadores de Lagrange

um método para resolver um problema de otimização sujeito a uma ou mais restrições

função objetiva

a função que deve ser maximizada ou minimizada em um problema de otimização

problema de otimização

cálculo de um valor máximo ou mínimo de uma função de várias variáveis, geralmente usando multiplicadores de Lagrange