14.1: Funções de várias variáveis

Last updated
Save as PDF

Page ID: 187968

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Reconheça uma função de duas variáveis e identifique seu domínio e alcance.
Esboce um gráfico de uma função de duas variáveis.
Esboce vários traços ou curvas de nível de uma função de duas variáveis.
Reconheça uma função de três ou mais variáveis e identifique suas superfícies niveladas.

Nosso primeiro passo é explicar o que é uma função de mais de uma variável, começando com funções de duas variáveis independentes. Essa etapa inclui identificar o domínio e a variedade dessas funções e aprender a representá-las graficamente. Também examinamos maneiras de relacionar os gráficos de funções em três dimensões com gráficos de funções planares mais familiares.

Funções de duas variáveis

A definição de uma função de duas variáveis é muito semelhante à definição de uma função de uma variável. A principal diferença é que, em vez de mapear valores de uma variável para valores de outra variável, mapeamos pares ordenados de variáveis para outra variável.

Definição: função de duas variáveis

Uma função de duas variáveis$z=f(x,y)$ mapeia cada par ordenado$(x,y)$ em um subconjunto$D$ do plano real$R^2$ para um número real exclusivo z. O conjunto$D$ é chamado de domínio da função. O intervalo de$f$ é o conjunto de todos os números reais z que tem pelo menos um par ordenado$(x,y)∈D$,$f(x,y)=z$ como mostrado na Figura$\PageIndex{1}$.

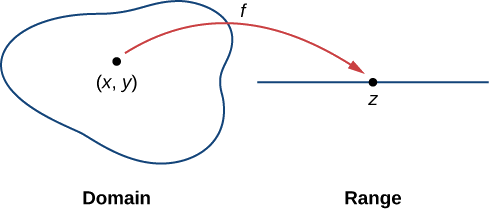
Uma forma bulbosa é marcada como domínio e contém o ponto (x, y). A partir desse ponto, há uma seta marcada com f que aponta para um ponto z em uma linha reta marcada como faixa. — Figura$\PageIndex{1}$: O domínio de uma função de duas variáveis consiste em pares ordenados$(x,y)$.

Determinar o domínio de uma função de duas variáveis envolve levar em consideração quaisquer restrições de domínio que possam existir. Vamos dar uma olhada.

Exemplo$\PageIndex{1}$: Domains and Ranges for Functions of Two Variables

Encontre o domínio e o alcance de cada uma das seguintes funções:

$f(x,y)=3x+5y+2$
$g(x,y)=\sqrt{9−x^2−y^2}$

Solução

a. Este é um exemplo de uma função linear em duas variáveis. Não há valores ou combinações de$x$ e$y$ que$f(x,y)$ façam com que seja indefinido, então o domínio de$f$ é$R^2$. Para determinar o intervalo, primeiro escolha um valor para z. Precisamos encontrar uma solução para a equação$f(x,y)=z,$ ou$3x−5y+2=z.$ uma dessas soluções pode ser obtida pela primeira configuração$y=0$, que produz a equação$3x+2=z$. A solução para essa equação é$x=\dfrac{z−2}{3}$, que fornece o par ordenado$\left(\dfrac{z−2}{3},0\right)$ como uma solução para a equação$f(x,y)=z$ para qualquer valor de$z$. Portanto, o intervalo da função é todo em números reais, ou$R$.

b. Para que$g(x,y)$ a função tenha um valor real, a quantidade abaixo da raiz quadrada não deve ser negativa:

\[ 9−x^2−y^2≥0. \nonumber \]

Essa desigualdade pode ser escrita na forma

\[ x^2+y^2≤9. \nonumber \]

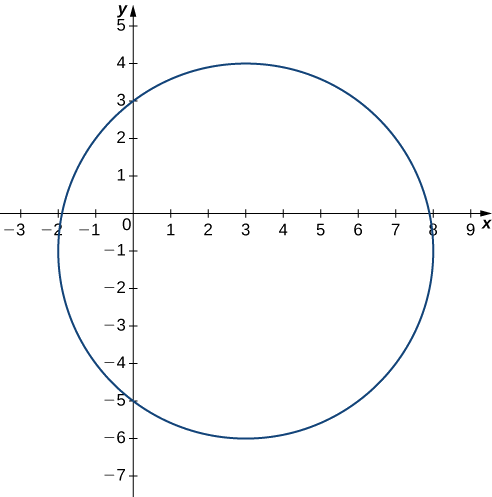
Portanto, o domínio de$g(x,y)$ é$\{(x,y)∈R^2∣x^2+y^2≤9\}$. O gráfico desse conjunto de pontos pode ser descrito como um disco de raio 3 centrado na origem. O domínio inclui o círculo limite, conforme mostrado no gráfico a seguir.

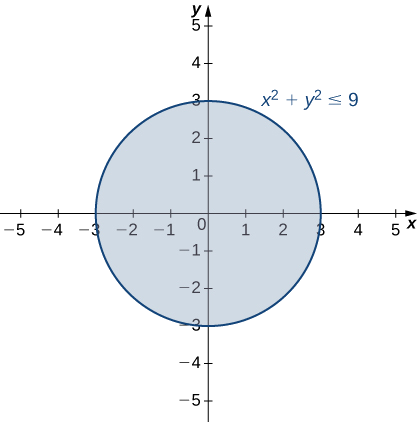
Um círculo de raio três com o centro na origem. A equação x2 + y2 = 9 é dada. — Figura$\PageIndex{2}$: O domínio da função$g(x,y)=\sqrt{9−x^2−y^2}$ é um disco fechado de raio 3.

Para determinar o alcance de,$g(x,y)=\sqrt{9−x^2−y^2}$ começamos com um ponto$(x_0,y_0)$ no limite do domínio, que é definido pela relação$x^2+y^2=9$. Daqui resulta que$x^2_0+y^2_0=9$ e

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0} \\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−9}\\[4pt] =0. \end{align*}\]

Se$x^2_0+y^2_0=0$ (em outras palavras$x_0=y_0=0)$, então

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0}\\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−0}=3. \end{align*}\]

Esse é o valor máximo da função. Dado qualquer valor$c$ entre$0$ e$3$, podemos encontrar um conjunto inteiro de pontos dentro do domínio de$g$ tal forma que$g(x,y)=c:$

\[\begin{align*} \sqrt{9−x^2−y^2} =c \\[4pt] 9−x^2−y^2 =c^2 \\[4pt] x^2+y^2 =9−c^2. \end{align*}\]

Uma vez que$9−c^2>0$, isso descreve um círculo de raio$\sqrt{9−c^2}$ centrado na origem. Qualquer ponto dessa circunferência satisfaz a equação$g(x,y)=c$. Portanto, o intervalo dessa função pode ser escrito em notação de intervalo como$[0,3].$

Exercício$\PageIndex{1}$

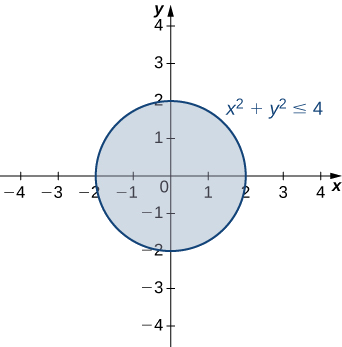
Encontre o domínio e o alcance da função$f(x,y)=\sqrt{36−9x^2−9y^2}$.

Dica

Determine o conjunto de pares ordenados que não tornam os radicandos negativos.

Solução

O domínio é$\{(x, y) | x^2+y^2≤4 \}$ o círculo sombreado definido pela desigualdade$x^2+y^2≤4$, que tem um círculo de raio$2$ como limite. O alcance é$[0,6].$

$Um círculo de raio dois com centro na origem. A equação x2 + y2 ≤ 4 é dada.$

Funções gráficas de duas variáveis

Suponha que desejemos representar graficamente a função.$z=f(x,y).$ Essa função tem duas variáveis independentes ($x$e$y$) e uma variável dependente$(z)$. Ao representar graficamente uma função$y=f(x)$ de uma variável, usamos o plano cartesiano. Somos capazes de representar graficamente qualquer par ordenado$(x,y)$ no plano, e cada ponto no plano tem um par ordenado$(x,y)$ associado a ele. Com uma função de duas variáveis, cada par ordenado$(x,y)$ no domínio da função é mapeado para um número real$z$. Portanto, o gráfico da função$f$ consiste em triplos ordenados$(x,y,z)$. O gráfico de uma função$z=f(x,y)$ de duas variáveis é chamado de superfície.

Para entender mais completamente o conceito de traçar um conjunto de triplos ordenados para obter uma superfície no espaço tridimensional, imagine o sistema de$(x,y)$ coordenadas plano. Então, cada ponto no domínio da função f tem um$z$ valor -exclusivo associado a ele. Se$z$ for positivo, então o ponto representado graficamente está localizado acima do$xy$ plano -, se$z$ for negativo, então o ponto representado graficamente está localizado abaixo do$xy$ plano -. O conjunto de todos os pontos representados graficamente se torna a superfície bidimensional que é o gráfico da função$f$.

Exemplo$\PageIndex{2}$: Graphing Functions of Two Variables

Crie um gráfico de cada uma das seguintes funções:

$g(x,y)=\sqrt{9−x^2−y^2}$
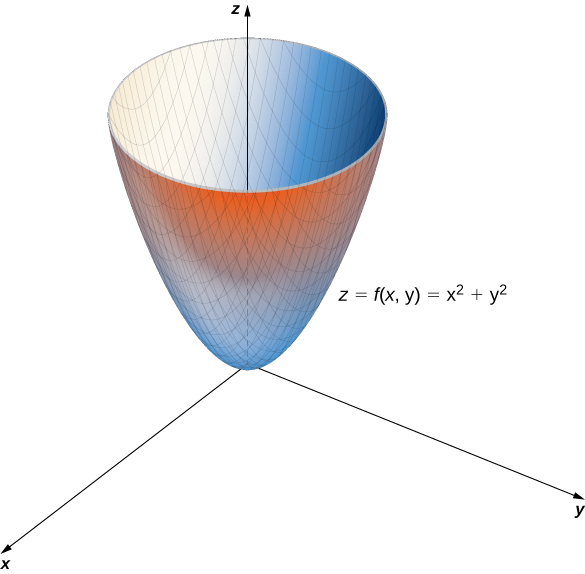
$f(x,y)=x^2+y^2$

Solução

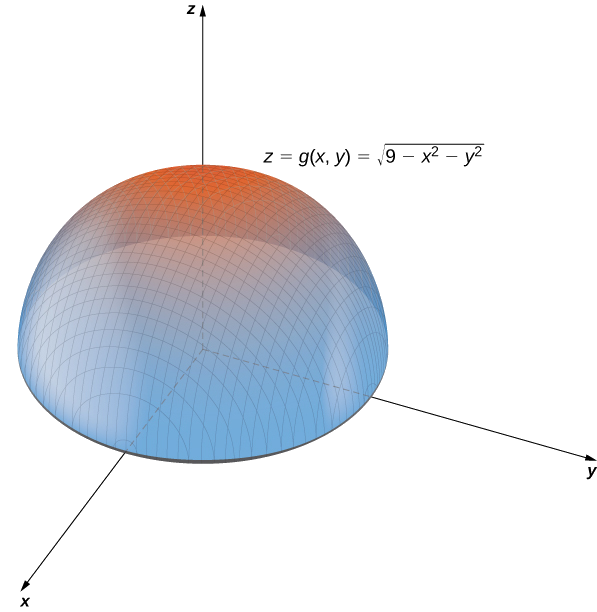
a. No exemplo$\PageIndex{2}$, determinamos que o domínio de$g(x,y)=\sqrt{9−x^2−y^2}$ é$\{(x,y)∈R^2∣x^2+y^2≤9\}$ e o intervalo são$\{z∈R^2∣0≤z≤3\}$. Quando$x^2+y^2=9$ temos$g(x,y)=0$. Portanto, qualquer ponto no círculo de raio$3$ centrado na origem no$xy$ plano -é mapeado para$z=0$ in$R^3$. Se$x^2+y^2=8$,$g(x,y)=1,$ então, qualquer ponto no círculo de raio$2\sqrt{2}$ centrado na origem no$xy$ plano -mapeia para$z=1$ in$R^3$. À medida$x^2+y^2$ que se aproxima de zero, o valor das$z$ aproximações$3$. Quando$x^2+y^2=0$, então$g(x,y)=3$. Essa é a origem no$xy$ plano -Se$x^2+y^2$ for igual a qualquer outro valor entre$0$ e$9$, então é$g(x,y)$ igual a alguma outra constante entre$0$$3$ e. A superfície descrita por esta função é um hemisfério centrado na origem com raio$3$, conforme mostrado no gráfico a seguir.

Um hemisfério com centro na origem. A equação z = g (x, y) = a raiz quadrada da quantidade (9 — x2 — y2) é dada. — Figura$\PageIndex{3}$: Gráfico do hemisfério representado pela função dada de duas variáveis.

b. Essa função também contém a expressão$x^2+y^2$. Definindo essa expressão igual a vários valores começando em zero, obtemos círculos de raio crescente. O valor mínimo de$f(x,y)=x^2+y^2$ é zero (alcançado quando$x=y=0.$. Quando$x=0$, a função se torna$z=y^2$, e quando$y=0$, então a função se torna$z=x^2$. Essas são seções transversais do gráfico e são parábolas. Lembre-se de Introdução aos Vectores no Espaço que o nome do gráfico de$f(x,y)=x^2+y^2$ é um parabolóide. O gráfico de$f$ aparece no gráfico a seguir.

Um parabolóide com vértice na origem. A equação z = f (x, y) = x2 + y2 é fornecida. — Figura$\PageIndex{4}$: Um parabolóide é o gráfico da função dada de duas variáveis.

Exemplo$\PageIndex{3}$: Nuts and Bolts

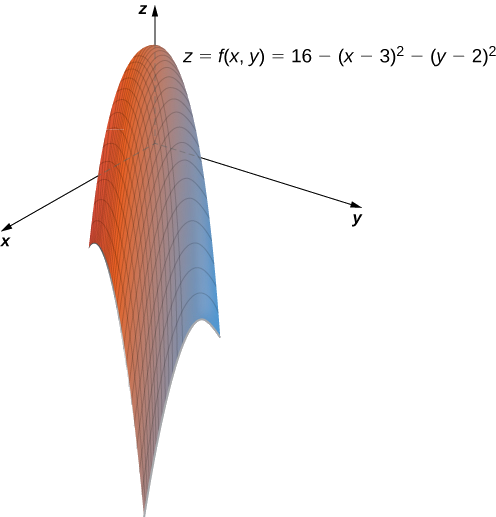
Uma função de lucro para um fabricante de hardware é dada por

\[f(x,y)=16−(x−3)^2−(y−2)^2, \nonumber \]

onde$x$ está o número de nozes vendidas por mês (medido em milhares) e$y$ representa o número de parafusos vendidos por mês (medido em milhares). O lucro é medido em milhares de dólares. Esboce um gráfico dessa função.

Solução

Essa função é uma função polinomial em duas variáveis. O domínio de$f$ consiste em pares de$(x,y)$ coordenadas que geram um lucro não negativo:

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 ≥ 0 \\[4pt] (x−3)^2+(y−2)^2 ≤ 16. \end{align*}\]

Este é um disco de raio$4$ centrado em$(3,2)$. Uma restrição adicional é que ambos$x$ e não$y$ devem ser negativos. Quando$x=3$ e$y=2, f(x,y)=16.$ Observe que é possível que qualquer valor não seja inteiro; por exemplo, é possível vender$2.5$ milhares de nozes em um mês. O domínio, portanto, contém milhares de pontos, então podemos considerar todos os pontos dentro do disco. Para qualquer um$z<16$, podemos resolver a equação$f(x,y)=16:$

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 =z \\[4pt] (x−3)^2+(y−2)^2 =16−z. \end{align*}\]

Como$z<16,$ sabemos disso$16−z>0,$, a equação anterior descreve uma circunferência com raio$\sqrt{16−z}$ centrado no ponto$(3,2)$. Portanto, o intervalo de$f(x,y)$ é$\{z∈\mathbb{R}|z≤16\}.$ O gráfico de também$f(x,y)$ é um parabolóide, e esse parabolóide aponta para baixo, conforme mostrado.

Um centro parabolóide aparentemente no eixo z positivo. A equação z = f (x, y) = 16 — (x — 3) 2 — (y — 2) 2 é dada. — Figura$\PageIndex{5}$: O gráfico da função dada de duas variáveis também é um parabolóide.

Curvas de nível

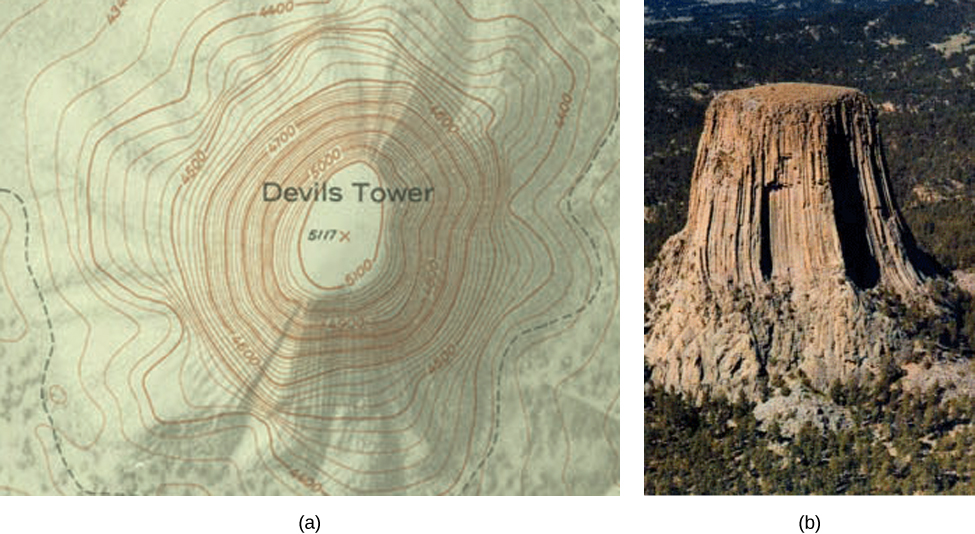
Se os caminhantes caminharem por trilhas acidentadas, eles podem usar um mapa topográfico que mostra a intensidade com que as trilhas mudam. Um mapa topográfico contém linhas curvas chamadas linhas de contorno. Cada linha de contorno corresponde aos pontos no mapa que têm igual elevação (Figura$\PageIndex{6}$). Uma curva de nível de uma função de duas variáveis$f(x,y)$ é completamente análoga a uma linha de contorno em um mapa topográfico.

Esta figura consiste em duas figuras marcadas a e b. A Figura a mostra um mapa topográfico da Torre do Diabo, que tem suas linhas muito próximas para indicar o terreno muito íngreme. A Figura b mostra uma imagem da Torre do Diabo, que tem lados muito íngremes. — Figura$\PageIndex{6}$: (a) Um mapa topográfico da Devil's Tower, Wyoming. Linhas próximas indicam terrenos muito íngremes. (b) Uma foto em perspectiva da Devil's Tower mostra o quão íngremes são suas laterais. Observe que o topo da torre tem a mesma forma do centro do mapa topográfico.

Definição: curvas de nível

Dada uma função$f(x,y)$ e um número$c$ na faixa de$f$, uma curva de nível de uma função de duas variáveis para o valor$c$ é definida como o conjunto de pontos que satisfazem a equação$f(x,y)=c.$

Retornando à função$g(x,y)=\sqrt{9−x^2−y^2}$, podemos determinar as curvas de nível dessa função. O intervalo de$g$ é o intervalo fechado$[0,3]$. Primeiro, escolhemos qualquer número nesse intervalo fechado — digamos,$c=2$. A curva de nível correspondente a$c=2$ é descrita pela equação

\[ \sqrt{9−x^2−y^2}=2. \nonumber \]

Para simplificar, eleve ao quadrado os dois lados dessa equação:

\[ 9−x^2−y^2=4. \nonumber \]

Agora, multiplique os dois lados da equação por$−1$ e adicione$9$ a cada lado:

\[ x^2+y^2=5. \nonumber \]

Essa equação descreve um círculo centrado na origem com raio$\sqrt{5}$. O uso de valores$c$ entre$0$ e$3$ produz outros círculos também centralizados na origem. Se$c=3$, então, o círculo tem raio$0$, então ele consiste apenas na origem. A figura$\PageIndex{7}$ é um gráfico das curvas de nível dessa função correspondente a$c=0,1,2,$$3$ e. Observe que, na derivação anterior, pode ser possível que tenhamos introduzido soluções extras ao quadrado dos dois lados. Esse não é o caso aqui porque o intervalo da função de raiz quadrada não é negativo.

Três círculos concêntricos com centro na origem. O maior círculo marcado com c = 0 tem um raio de 3. O círculo médio marcado com c = 1 tem um raio ligeiramente menor que 3. O menor círculo marcado com c = 2 tem um raio ligeiramente maior que 2. — Figura$\PageIndex{7}$: Curvas de nível da função$g(x,y)=\sqrt{9−x^2−y^2}$, usando$c=0,1,2,$ e$3 (c=3$ corresponde à origem).

Um gráfico das várias curvas de nível de uma função é chamado de mapa de contorno.

Exemplo$\PageIndex{4}$: Making a Contour Map

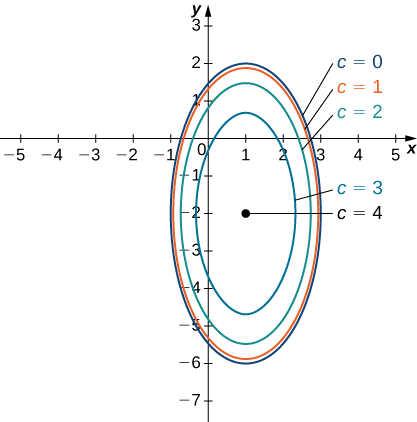
Dada a função$f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}$, encontre a curva de nível correspondente$c=0$ a. Em seguida, crie um mapa de contorno para essa função. Quais são o domínio e a variedade de$f$?

Solução

Para encontrar a curva de nível,$c=0,$ definimos$f(x,y)=0$ e resolvemos. Isso dá

$0=\sqrt{8+8x−4y−4x^2−y^2}$.

Em seguida, quadramos os dois lados e multiplicamos os dois lados da equação por$−1$:

$4x^2+y^2−8x+4y−8=0.$

Agora, reorganizamos os termos, juntando os$x$ termos e os$y$ termos juntos, e adicionamos$8$ a cada lado:

$4x^2−8x+y^2+4y=8.$

Em seguida, agrupamos os pares de termos contendo a mesma variável entre parênteses e o fator$4$ do primeiro par:

$4(x^2−2x)+(y^2+4y)=8.$

Em seguida, completamos o quadrado em cada par de parênteses e adicionamos o valor correto ao lado direito:

$4(x^2−2x+1)+(y^2+4y+4)=8+4(1)+4.$

Em seguida, fatoramos o lado esquerdo e simplificamos o lado direito:

$4(x−1)^2+(y+2)^2=16.$

Por último, dividimos os dois lados por$16:$

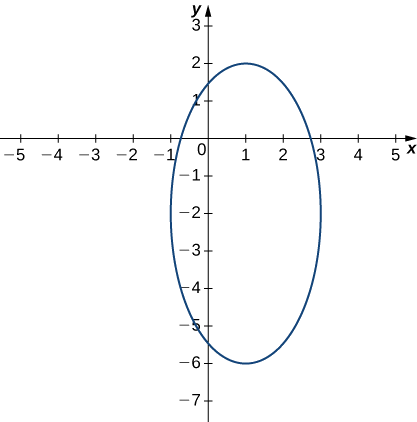
$\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}=1.\label{conteq0}$

Esta equação descreve uma elipse centrada em$(1,−2).$ O gráfico dessa elipse aparece no gráfico a seguir.

Uma elipse com centro (1, —2), eixo maior vertical e comprimento 8 e eixo menor horizontal de comprimento 4. — Figura$\PageIndex{8}$: Curva de nível da função$f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}$ correspondente a$c=0$

Podemos repetir a mesma derivação para valores$c$ menores que$4.$ Então, a Equação\ ref {conteq0} se torna

$\dfrac{4(x−1)^2}{16−c^2}+\dfrac{(y+2)^2}{16−c^2}=1$

por um valor arbitrário de$c$. A figura$\PageIndex{9}$ mostra um mapa de contorno para$f(x,y)$ usar os valores$c=0,1,2,$$3$ e. Quando$c=4,$ a curva de nível é o ponto$(−1,2)$.

Uma série de quatro elipses concêntricas com centro (1, —2). O maior está marcado com c = 0 e tem eixo maior vertical e de comprimento 8 e eixo menor horizontal de comprimento 4. O próximo menor está marcado com c = 1 e é apenas um pouco menor. Os próximos dois estão marcados com c = 2 e c = 3 e são cada vez menores. Finalmente, há um ponto marcado com c = 4 no centro (1, —2). — Figura$\PageIndex{9}$: Mapa de contorno da função$f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}$ usando os valores$c=0,1,2,3,$$4$ e.

Encontrando o domínio e o alcance

Como essa é uma função de raiz quadrada, o radicando não deve ser negativo. Então nós temos

\[8+8x−4y−4x^2−y^2\ge 0 \nonumber \]

Reconhecendo que o limite do domínio é uma elipse, repetimos as etapas mostradas acima para obter

\[\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}\le 1 \nonumber \]

Portanto, o domínio de$f$ pode ser escrito:$\big\{ (x,y) \,|\, \frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}\le 1 \big\}.$

Para encontrar o intervalo de,$f,$ precisamos considerar as possíveis saídas dessa função de raiz quadrada. Sabemos que a saída não pode ser negativa, então precisamos verificar se a saída é alguma vez.$0.$ Do trabalho que concluímos acima para encontrar a curva de nível, pois$c = 0,$ sabemos que o valor de$f$ é$0$ para qualquer ponto dessa curva de nível (na elipse,$\frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}=1$). Portanto, sabemos que o limite inferior do intervalo dessa função é$0.$

Para determinar o limite superior do intervalo da função nesse problema, é mais fácil se primeiro completarmos o quadrado abaixo do radical.

\ [\ begin {align*} f (x, y) &=\ sqrt {8+8x−4y−4x^2−y^2}\\ [5pt]
&=\ sqrt {8 - 4 (x^2 - 2x\ quad) - (y^2 + 4y\ quad)}\\ [5pt]
&=\ sqrt {8 - 4 (x^2) - 2x +1 - 1) - (y^2 + 4y + 4 - 4)}\\ [5pt]
&=\ sqrt {8 - 4 (x^2 - 2x +1) + 4 - (y^2 + 4y + 4) +4}\\ [5pt]
&=\ sqrt {16 - 4 (x-1) ^2 - (y+2) ^2}\ end {align*}\]

Agora que temos$f$ esse formulário, podemos ver o tamanho do radicando. Como estamos subtraindo dois quadrados perfeitos de,$16,$ sabemos que o valor do radicando não pode ser maior do que$16.$ No ponto em que$(1, -2),$ podemos ver que o radicando será 16 (já que subtrairemos neste$0$$16$ ponto). Isso nos dá o valor máximo de$f$, ou seja$f(1, -2) = \sqrt{16} = 4.$

Portanto, o alcance dessa função é$[0, 4].$

Exercício$\PageIndex{2}$

Encontre e represente graficamente a curva de nível da função$g(x,y)=x^2+y^2−6x+2y$ correspondente a$c=15.$

Dica

Primeiro, defina$g(x,y)=15$ e depois complete o quadrado.

Solução

A equação da curva de nível pode ser escrita como$(x−3)^2+(y+1)^2=25,$ que é um círculo com raio$5$ centrado em$(3,−1).$

$Um círculo de raio 5 com centro (3, —1).$

Outra ferramenta útil para entender o gráfico de uma função de duas variáveis é chamada de traço vertical. As curvas de nível são sempre representadas graficamente no$xy-plane$, mas, como o nome indica, os traços verticais são representados graficamente nos$yz$ planos$xz$ - ou.

Definição: traços verticais

Considere uma função$z=f(x,y)$ com domínio$D⊆\mathbb{R}^2$. Um traço vertical da função pode ser o conjunto de pontos que resolve a equação$f(a,y)=z$ para uma determinada constante$x=a$ ou$f(x,b)=z$ para uma determinada constante.$y=b.$

Exemplo$\PageIndex{5}$: Finding Vertical Traces

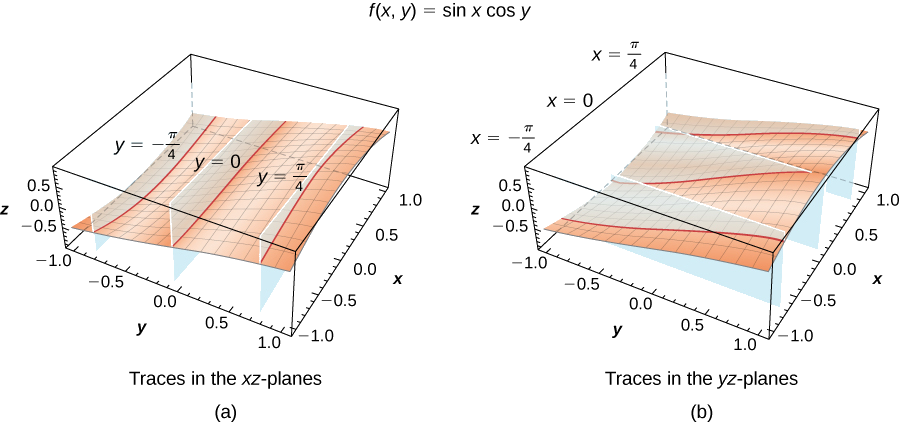
Encontre traços verticais para a função$f(x,y)=\sin x \cos y$ correspondente a$x=−\dfrac{π}{4},0,$ e$\dfrac{π}{4}$$y=−\dfrac{π}{4},0$, e$\dfrac{π}{4}$ e.

Solução

Primeiro conjunto$x=−\dfrac{π}{4}$ na equação$z=\sin x \cos y:$

$z=\sin(−\dfrac{π}{4})\cos y=−\dfrac{\sqrt{2}\cos y}{2}≈−0.7071\cos y.$

Isso descreve um gráfico de cosseno no plano$x=−\dfrac{π}{4}$. Os outros valores de z aparecem na tabela a seguir.

Traços verticais paralelos$xz-Plane$ aos da função$f(x,y)=\sin x \cos y$
$c$	Rastreamento vertical para$x=c$
\ (c\)” style="alinhamento vertical: médio; ">$−\dfrac{π}{4}$	\ (x=c\)” style="alinhamento vertical: médio; ">$z=−\dfrac{\sqrt{2}\cos y}{2}$
\ (c\)” style="alinhamento vertical: médio; ">0	\ (x=c\)” style="alinhamento vertical: médio; ">$z=0$
\ (c\)” style="alinhamento vertical: médio; ">$\dfrac{π}{4}$	\ (x=c\)” style="alinhamento vertical: médio; ">$z=\dfrac{\sqrt{2}\cos y}{2}$

De forma semelhante, podemos substituir o$y-values$ na equação$f(x,y)$ para obter os traços$yz-plane,$ conforme listado na tabela a seguir.

Traços verticais paralelos$yz-Plane$ aos da função$f(x,y)=\sin x \cos y$
$d$	Rastreamento vertical para$y=d$
\ (d\)” style="alinhamento vertical: médio; ">$\dfrac{π}{4}$	\ (y=d\)” style="alinhamento vertical: médio; ">$z=\dfrac{\sqrt{2}\sin x}{2}$
\ (d\)” style="alinhamento vertical: médio; ">0	\ (y=d\)” style="alinhamento vertical: médio; ">$z=\sin x$
\ (d\)” style="alinhamento vertical: médio; ">$−\dfrac{π}{4}$	\ (y=d\)” style="alinhamento vertical: médio; ">$z=\dfrac{\sqrt{2}\sin x}{2}$

Os três traços no$xz-plane$ são funções de cosseno; os três traços na$yz-plane$ são funções senoidais. Essas curvas aparecem nas interseções da superfície com os planos$x=−\dfrac{π}{4},x=0,x=\dfrac{π}{4}$ e$y=−\dfrac{π}{4},y=0,y=\dfrac{π}{4}$ conforme mostrado na figura a seguir.

Esta figura consiste em duas figuras marcadas a e b. Na figura a, uma função é dada em três dimensões e é intersectada por três planos x-z paralelos em y = ±π /4 e 0. Na figura b, uma função é dada em três dimensões e é intersectada por três planos y-z paralelos em x = ±π /4 e 0. — Figura$\PageIndex{10}$: Traços verticais da função$f(x,y)$ são curvas de cosseno em$xz-planes$ (a) e curvas senoidais em$yz-planes$ (b).

Exercício$\PageIndex{3}$

Determine a equação do traço vertical da função$g(x,y)=−x^2−y^2+2x+4y−1$ correspondente e descreva seu gráfico.$y=3$

Dica: $y=3$Defina a equação$z=−x^2−y^2+2x+4y−1$ e complete o quadrado.
Solução: $z=3−(x−1)^2$. Esta função descreve uma parábola que se abre para baixo no plano$y=3$.

Funções de duas variáveis podem produzir algumas superfícies de aparência impressionante. A figura$\PageIndex{11}$ mostra dois exemplos.

Esta figura consiste em duas figuras marcadas a e b. Na figura a, a função f (x, y) = x2 sin y é dada; ela tem algumas propriedades senoidais aumentando à medida que o quadrado ao longo dos máximos da função seno. Na figura b, a função f (x, y) = sin (ex) cos (ln y) é dada em três dimensões; ela diminui suavemente a partir do canto mais próximo (—2, 20), mas depois parece se agrupar em uma série de dobras paralelas aos eixos x e y. — Figura$\PageIndex{11}$: Exemplos de superfícies representando funções de duas variáveis: (a) uma combinação de uma função de potência e uma função senoidal e (b) uma combinação de funções trigonométricas, exponenciais e logarítmicas.

Funções de mais de duas variáveis

Até agora, examinamos apenas funções de duas variáveis. No entanto, é útil dar uma breve olhada nas funções de mais de duas variáveis. Dois desses exemplos são

\[ \underbrace{f(x,y,z)=x^2−2xy+y^2+3yz−z^2+4x−2y+3x−6}_{\text{a polynomial in three variables}} \nonumber \]

\[g(x,y,t)=(x^2−4xy+y^2)\sin t−(3x+5y)\cos t. \nonumber \]

Na primeira função,$(x,y,z)$ representa um ponto no espaço, e a função$f$ mapeia cada ponto no espaço para uma quarta quantidade, como temperatura ou velocidade do vento. Na segunda função,$(x,y)$ pode representar um ponto no plano e$t$ pode representar o tempo. A função pode mapear um ponto no plano para uma terceira quantidade (por exemplo, pressão) em um determinado momento$t$. O método para encontrar o domínio de uma função de mais de duas variáveis é análogo ao método para funções de uma ou duas variáveis.

Exemplo$\PageIndex{6}$: Domains for Functions of Three Variables

Encontre o domínio de cada uma das seguintes funções:

$f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}$
$g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}$

Solução:

a. Para que$f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}$ a função seja definida (e seja um valor real), duas condições devem ser válidas:

O denominador não pode ser zero.
O radicando não pode ser negativo.

A combinação dessas condições leva à desigualdade

\[9−x^2−y^2−z^2>0.\nonumber \]

Mover as variáveis para o outro lado e reverter a desigualdade dá ao domínio como

\[domain(f)=\{(x,y,z)∈R^3∣x^2+y^2+z^2<9\},\nonumber \]

que descreve uma bola de raio$3$ centrada na origem. (Nota: A superfície da bola não está incluída neste domínio.)

b. Para que$g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}$ a função seja definida (e seja um valor real), duas condições devem ser válidas:

O radicando não pode ser negativo.
O denominador não pode ser zero.

Como o radicando não pode ser negativo, isso implica e$2t−4≥0$, portanto, aquilo$t≥2$. Como o denominador não pode ser zero$x^2−y^2≠0$,, ou$x^2≠y^2$, Que pode ser reescrito como$y=±x$, quais são as equações de duas retas passando pela origem. Portanto, o domínio de$g$ é

\[ domain(g)=\{(x,y,t)|y≠±x,t≥2\}. \nonumber \]

Exercício$\PageIndex{4}$

Encontre o domínio da função$h(x,y,t)=(3t−6)\sqrt{y−4x^2+4}$.

Dica: Verifique os valores que tornam os radicandos negativos ou os denominadores iguais a zero.
Solução: \[domain(h)=\{(x,y,t)\in \mathbb{R}^3∣y≥4x^2−4\} \nonumber \]

As funções de duas variáveis têm curvas de nível, que são mostradas como curvas no$xy-plane.$ No entanto, quando a função tem três variáveis, as curvas se tornam superfícies, então podemos definir superfícies de nível para funções de três variáveis.

Definição: superfície nivelada de uma função de três variáveis

Dada uma função$f(x,y,z)$ e um número$c$ na faixa de$f$, uma superfície nivelada de uma função de três variáveis é definida como o conjunto de pontos que satisfazem a equação$f(x,y,z)=c.$

Exemplo$\PageIndex{7}$: Finding a Level Surface

Encontre a superfície nivelada para a função$f(x,y,z)=4x^2+9y^2−z^2$ correspondente$c=1$ a.

Solução

A superfície nivelada é definida pela equação$4x^2+9y^2−z^2=1.$ Esta equação descreve um hiperbolóide de uma folha, conforme mostrado na Figura$\PageIndex{12}$.

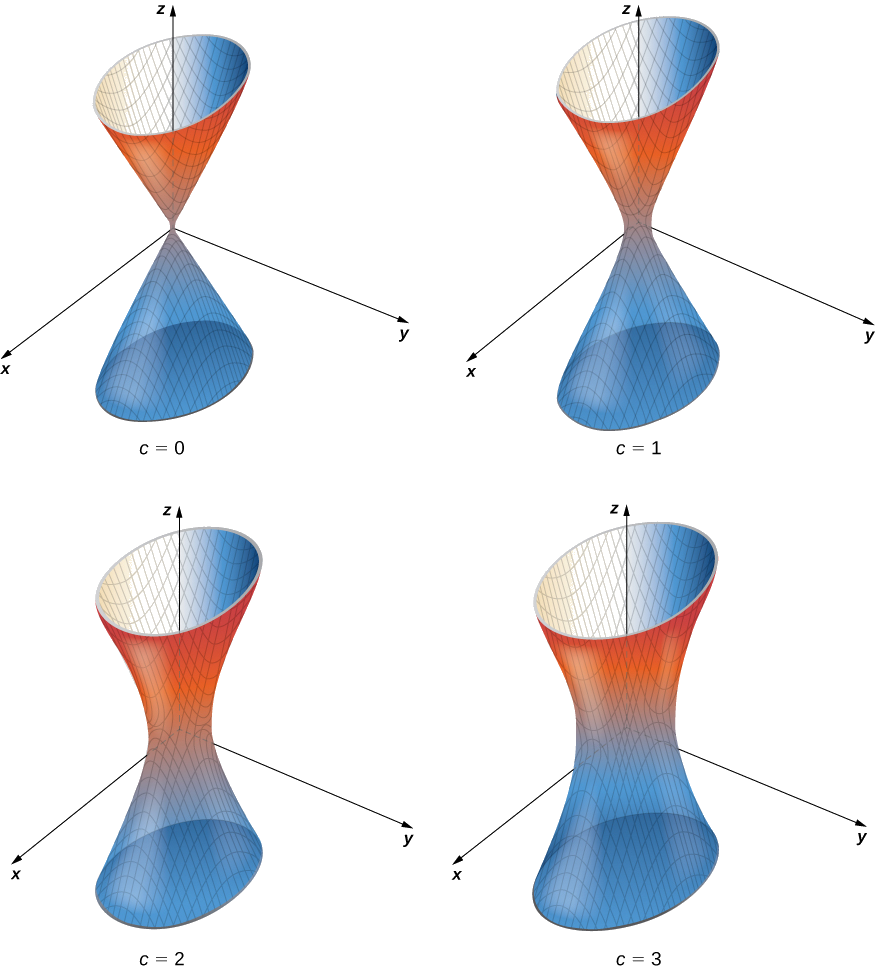
Esta figura é composta por quatro figuras. O primeiro está marcado com c = 0 e consiste em um cone duplo (ou seja, duas nappes) com seu ápice na origem. A segunda está marcada com c = 1 e parece notavelmente semelhante à primeira, exceto que não há ápice no qual os cones se encontrem: em vez disso, as duas nappes estão conectadas. Da mesma forma, a próxima figura marcada com c = 2 faz com que as duas nappes se conectem, mas desta vez a conexão é maior (ou seja, o raio de sua conexão é maior). A figura final marcada com c = 3 também tem as duas nappes conectadas de uma forma ainda maior. — Figura$\PageIndex{12}$: Um hiperbolóide de uma folha com algumas de suas superfícies niveladas.

Exercício$\PageIndex{5}$

Encontre a equação da superfície nivelada da função

\[ g(x,y,z)=x^2+y^2+z^2−2x+4y−6z \nonumber \]

correspondendo$c=2,$ e descrevendo a superfície, se possível.

Dica: Defina$g(x,y,z)=c$ e complete o quadrado.
Solução: ((x−1) ^2+ (y+2) ^2+ (z−3) ^2=16\) descreve uma esfera de raio$4$ centrada no ponto$(1,−2,3).$

Resumo

O gráfico de uma função de duas variáveis é uma superfície em$\mathbb{R}^3$ e pode ser estudado usando curvas de nível e traços verticais.
Um conjunto de curvas de nível é chamado de mapa de contorno.

Equações-chave

Traço vertical

$f(a,y)=z$para$x=a$ ou$f(x,b)=z$ para$y=b$

Superfície de nível de uma função de três variáveis

$f(x,y,z)=c$

Glossário

mapa de contorno: um gráfico das várias curvas de nível de uma determinada função$f(x,y)$

função de duas variáveis: uma função$z=f(x,y)$ que mapeia cada par ordenado$(x,y)$ em um subconjunto$D$ de$R^2$ para um número real exclusivo$z$

gráfico de uma função de duas variáveis: um conjunto de triplos ordenados$(x,y,z)$ que satisfaz a equação$z=f(x,y)$ traçada no espaço cartesiano tridimensional

curva de nível de uma função de duas variáveis: o conjunto de pontos que satisfaz a equação$f(x,y)=c$ para algum número real$c$ na faixa de$f$

superfície de nível de uma função de três variáveis: o conjunto de pontos que satisfaz a equação$f(x,y,z)=c$ para algum número real$c$ na faixa de$f$

superfície: o gráfico de uma função de duas variáveis,$z=f(x,y)$

traço vertical: o conjunto de triplos ordenados$(c,y,z)$ que resolve a equação$f(c,y)=z$ para uma determinada constante$x=c$ ou o conjunto de triplos ordenados$(x,d,z)$ que resolve a equação$f(x,d)=z$ para uma determinada constante$y=d$

\(c\)	Rastreamento vertical para\(x=c\)
\ (c\)” style="alinhamento vertical: médio; ">\(−\dfrac{π}{4}\)	\ (x=c\)” style="alinhamento vertical: médio; ">\(z=−\dfrac{\sqrt{2}\cos y}{2}\)
\ (c\)” style="alinhamento vertical: médio; ">0	\ (x=c\)” style="alinhamento vertical: médio; ">\(z=0\)
\ (c\)” style="alinhamento vertical: médio; ">\(\dfrac{π}{4}\)	\ (x=c\)” style="alinhamento vertical: médio; ">\(z=\dfrac{\sqrt{2}\cos y}{2}\)

\(d\)	Rastreamento vertical para\(y=d\)
\ (d\)” style="alinhamento vertical: médio; ">\(\dfrac{π}{4}\)	\ (y=d\)” style="alinhamento vertical: médio; ">\(z=\dfrac{\sqrt{2}\sin x}{2}\)
\ (d\)” style="alinhamento vertical: médio; ">0	\ (y=d\)” style="alinhamento vertical: médio; ">\(z=\sin x\)
\ (d\)” style="alinhamento vertical: médio; ">\(−\dfrac{π}{4}\)	\ (y=d\)” style="alinhamento vertical: médio; ">\(z=\dfrac{\sqrt{2}\sin x}{2}\)

Definição: função de duas variáveis

Exemplo\(\PageIndex{1}\): Domains and Ranges for Functions of Two Variables

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Graphing Functions of Two Variables

Exemplo\(\PageIndex{3}\): Nuts and Bolts

Definição: curvas de nível

Exemplo\(\PageIndex{4}\): Making a Contour Map

Exercício\(\PageIndex{2}\)

Definição: traços verticais

Exemplo\(\PageIndex{5}\): Finding Vertical Traces

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{6}\): Domains for Functions of Three Variables

Exercício\(\PageIndex{4}\)

Definição: superfície nivelada de uma função de três variáveis

Exemplo\(\PageIndex{7}\): Finding a Level Surface

Exercício\(\PageIndex{5}\)